核心素養下的高中數學教學探究

江蘇省鄭集高級中學 杜言言

高中數學核心素養是在對高中數學知識全面把握的基礎上概括而成的，其包括基本的數學知識及綜合的數學能力，強調學生數學能力的提升，因此，教學中應與時俱進，既要注重以往教學經驗的應用，又要注重核心素養內容的融入，使學生扎實掌握數學知識，同時實現核心素養的提升，終身受益。

一、落實核心素養，重視數學抽象知識講解

數學抽象是從數學角度研究問題的關鍵環節。眾所周知，多數數學知識來源于生活，而與生活中的問題有所不同，是生活問題的數學化。數學抽象在鍛煉學生邏輯思維、靈活運用所學上效果顯著。高中數學教學中應重視數學抽象，一方面，灌輸數學抽象知識，講解數學知識時，不能單純地告知學生結論，而應注重講解數學知識的抽象過程，使學生認識到數學抽象的重要性；另一方面，做好數學抽象訓練，可結合具體教學內容創設相關問題情境，要求學生進行抽象，運用所學的數學知識解決相關問題。

例如，在講解“數列”知識時，給出以下題目對學生進行訓練：在考試中，如果按照順序將一些高分去掉，那么班級的平均分會降低。同理，如將一些低分去掉，則平均分會提高。用數學語言對其進行如下描述：如果a1，a2，a3，…，an滿足a1≤a2≤…≤an，那么上述兩種情境用數學式子可表示為：____和_____。

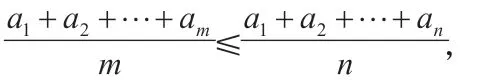
二、落實核心素養，加強邏輯推理能力訓練

邏輯推理是學好高中數學的重要能力，是核心素養體系的重要構成。眾所周知，邏輯推理對學生的思維、推理能力要求較高，教學中需要制定長遠計劃，做好長久的邏輯推理能力培養計劃。一方面，灌輸邏輯推理知識。為使學生掌握邏輯推理技巧，教學中，應為學生講解歸納、類比、演繹等推理形式，明確推理的步驟，使學生掌握基本的邏輯推理知識。另一方面，提升邏輯推理能力。邏輯推理能力的提升與堅持不懈的訓練不可分割，因此在教學中應創設經典問題情境，鼓勵學生進行推理，使學生在訓練中邏輯推理更為縝密。

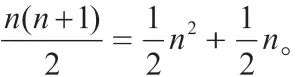
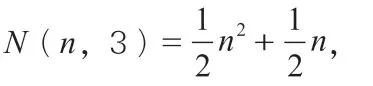
當k=4 時，N（n，4）=n2，

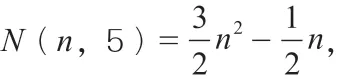
求解N（10，24）的值。

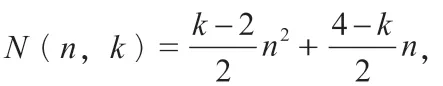
三、落實核心素養，促進直觀想象能力的提升

直觀想象與圖形密切相關。高中數學中的圖形包括平面圖形、立體圖形，因此，教學中應圍繞數學中的“圖形”開展教學工作，促進學生直觀想象能力的提升。教學中應注重以下內容的落實：一方面，明確直觀想象范圍。理論上借助圖形研究線線位置、點面位置、面面位置、點的運動等都可提高學生的直觀想象能力，如高中數學中的解析幾何、立體幾何等內容以及相關習題等，因此，教學中在講解這些內容時，應有意識地培養學生的直觀想象能力。另一方面，提高例題講解質量。為提高學生的直觀想象能力，講解例題時應做好研究，明確例題考查的知識點以及是如何提高直觀想象能力的，深思熟慮，讓學生解好題。

例如，在講解“立體幾何”知識時，為提高學生的直觀想象能力，可引入以下例題：如圖1 所示的ABCD-A1B1C1D1為正四棱柱，在平面A1B1C1D1的內部存在一點P，則三棱錐P-BCD的正視圖和側視圖的面積之比為（ ）

A. 1 ∶1 B. 2 ∶1

C. 2 ∶3 D. 3 ∶2

該例題立足立體幾何中的視圖問題巧妙設問，可很好地培養學生的直觀想象能力。教學中為幫助學生更加深刻地理解，可借助多媒體技術向學生動態展示正視圖和側視圖。通過多媒體課件可知，三棱錐的正視圖為三角形，底邊數值等于正四棱錐的底面邊長，高就是正四棱柱的高，側視圖也是三角形，對應的數值和正視圖看到的一樣，因此，兩者的面積相等，面積之比應為1 ∶1，正確結果選A。

總之，在當前教育領域比較關注“立德樹人”的背景下，培養學生的核心素養成為高中數學教學工作關注的重點。教學中不僅要做好課程標準研究，明確教學目標與教學要求，而且還應積極踐行核心素養培養工作。本文通過研究認為，一方面，培養學生核心素養不是一朝一夕就可完成的，需要制定長遠計劃，確立長期與近期目標，按部就班地開展培養工作；另一方面，吃透核心素養內涵，明確核心素養包含的內容，巧妙融入高中數學知識、習題講解中，提高學生數學成績，同時順利完成核心素養培養目標。