基于人群搜索自抗擾控制的放卷張力控制系統

丁 孟，趙世海

(1.天津工業大學 機械工程學院，天津 300387； 2.天津市現代機電裝備技術重點實驗室，天津 300387)

張力系統作為連續軋染機的重要組成部分，其控制精度和穩定性對保證連續軋染產品的質量至關重要。織物放卷是連續軋染生產的第1步，若張力產生了波動則會影響織物的生產加工質量，對后續的生產加工過程也會造成影響[1-2]。在軋染機放卷運行過程中，由于織物料卷卷徑發生變化，引起織物料卷輥轉動慣量的變化，結合外部擾動和擺輥引起的織物料帶長度變化等影響因素，從而導致放卷織物產生的張力出現波動[3]。放卷張力系統是具有強耦合和強干擾的非線性時變系統，因此，保證放卷張力系統的穩定運行，可以設計實現解耦控制和抗干擾性的控制器，對軋染機放卷張力控制非常重要。

目前，隨著軋染生產加工工藝的復雜化，對連續軋染機生產加工的要求也越來越高，傳統PID(比例積分微分)控制已經不能滿足現代化的生產加工要求。近年來，越來越多的現代控制方法在張力控制中得到應用。李建等[4]將魯棒控制應用于印染機卷繞張力控制系統中，實現了張力系統的穩定運行。湯偉等[5]提出利用模糊自適應PID的控制方法來解決懸浮包裝中薄膜張力控制難的問題，實現了薄膜張力的穩定控制。王友釗等[6]采用神經網絡對織機卷繞系統的張力進行控制，提高了卷繞系統的控制性能。但是上述控制方法都是建立在精準數學模型的基礎上，實現良好的控制性能，而在工程應用中由于許多因素的影響，難以建立精準的模型，因而影響了這些方法的使用。

本文針對軋染機放卷張力控制問題，結合人群搜索算法(SOA)[7-9]和自抗擾控制(ADRC)，建立了人群搜索自抗擾控制器，將放卷張力系統中難以建模和內外擾動等影響因素通過非線性擴張觀測器實現估計和補償，并用人群搜索算法對ADRC中的參數進行整定[10-12]，通過仿真結果得出人群搜索自抗擾控制器可以實現解耦控制和內外界擾動的補償，保證了放卷張力系統恒張力運行。

1 系統數學模型的建立

軋染機放卷張力系統包括放卷部分和牽引部分，主要實現系統的恒張力控制。圖1為放卷張力系統結構圖。放卷電動機和牽引電動機采用伺服電動機驅動，并使用擺輥來檢測和調節張力波動。

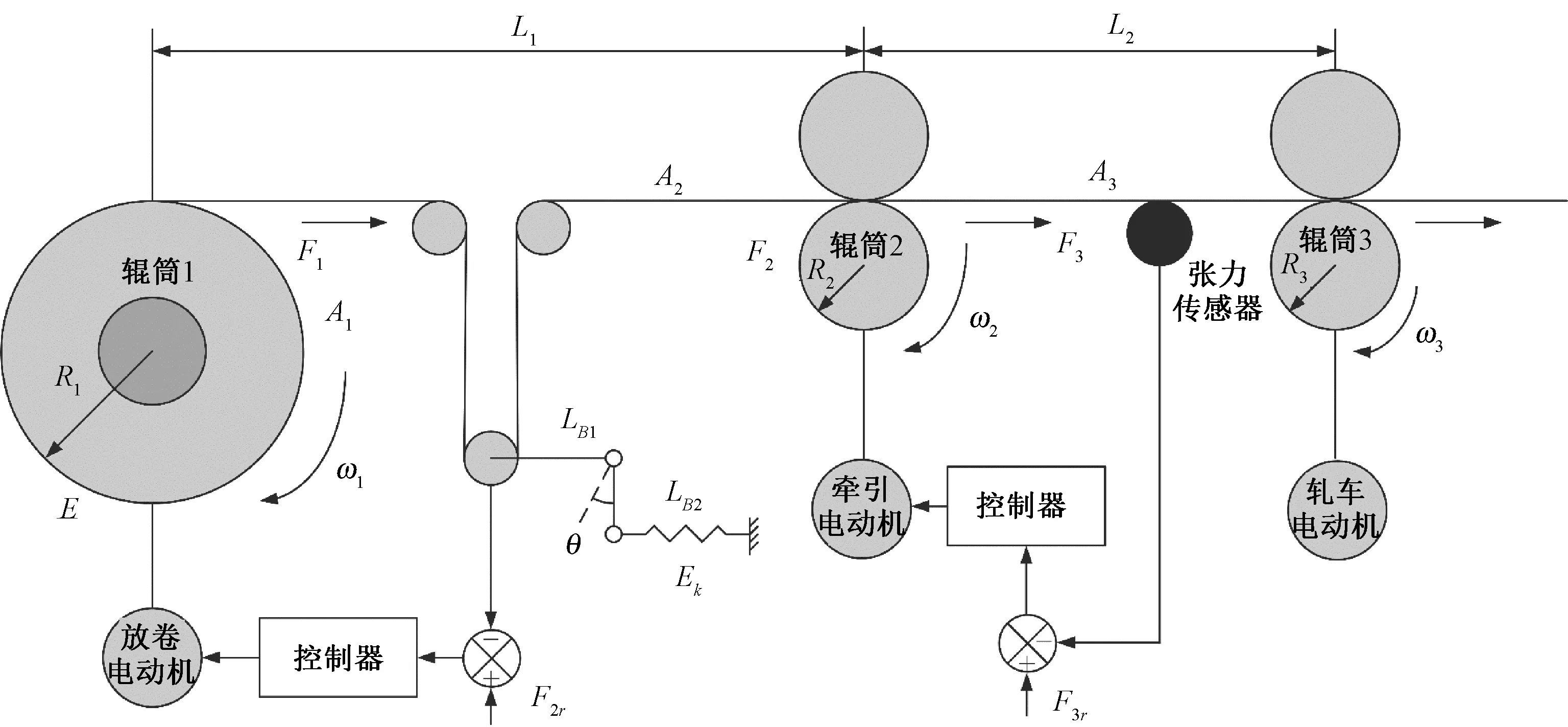
圖1 放卷張力系統結構圖

圖1中：L1、L2為輥間織物長度，m；E為織物彈性模量，Pa；Ek為擺輥臂等效彈簧的彈性模量，Pa；Ai(i=1,2,3)為織物橫截面積，m2；Ri(i=1,2,3)為各織物輥半徑，m；ωi(i=1,2,3)為各織物輥角速度，r/min；Fi(i=1,2,3)為織物各部分張力，N；LBi(i=1,2)為擺臂輥各部分長度，m；Fir(i=2,3)為織物各部分張力設定值，N。

在軋染機放卷過程中，假設織物與織物輥間的運動為純滾動，并且織物發生純彈性變形，基于連續軋染機的工作原理，根據放卷張力系統中織物料帶的質量守恒定律、擺輥及各輥的動力學原理，可得連續軋染機放卷張力系統的數學模型為：

(1)

式中：J1、J2為織物輥轉動慣量，kg·m2；JBa為擺臂輥轉動慣量，kg·m2；f、fB分別為織物輥、擺臂輥的摩擦阻尼系數；MR1(t)、MR2(t)為各伺服電動機的轉矩，N·m。

對F2(t)、F3(t)求二階導數得：

(2)

由放卷模型表明其系統具有耦合性。通過對系統模型解耦分析得到狀態空間模型，見式(3)：

(3)

式中：D(t)為系統中無輸入量的動態耦合；P(t)MR(t)為有輸入量靜態耦合。

(4)

(5)

(6)

取靜態耦合為H(t)=P(t)MR(t)，H(t)為虛擬控制量，則模型見式(7):

(7)

由于|P(t)|≠0，則MR(t)=P(t)-1H(t)，P(t)-1為靜態解耦矩陣，見式(8)：

(8)

通過對上述模型分析，在引入虛擬控制量H(t)后，使放卷張力系統實現了靜態解耦控制，只需將系統中動態耦合和內外部擾動估計補償掉，就能夠保證系統完全解耦控制。

2 人群搜索自抗擾控制器設計

通過對軋染機放卷張力系統模型的分析，設計二階人群搜索自抗擾(SOA-ADRC)控制器，人群搜索自抗擾控制器結構圖見圖2。

由圖2可以看出，該結構主要包括安排過渡過程的跟蹤微分器(TD)、非線性狀態誤差反饋率(NLSEF)、實現干擾估計補償的擴張狀態觀測器(ESO)，以及對參數進行調整的人群搜索(SOA)控制器。

2.1 自抗擾控制器

自抗擾控制器由TD、NLSEF 與ESO 3個部分構成。TD部分用vi1來跟蹤系統中各段張力Fir信號，且由vi2跟蹤提取張力Fir的微分信號。ESO部分對參數βi1、βi2、βi3進行合理調整，獲得對系統輸出張力Fi、Fi微分的跟蹤估計值zi1、zi2，及動態耦合與內外干擾的估計值zi3。NLSEF部分用來分別對跟蹤張力的差值ei1和微分差值ei2的控制量安排合理的分配重組，并對系統的擾動進行補償。根據人群搜索算法，實現對自抗擾控制器中參數的整定，保證系統可以穩定運行。

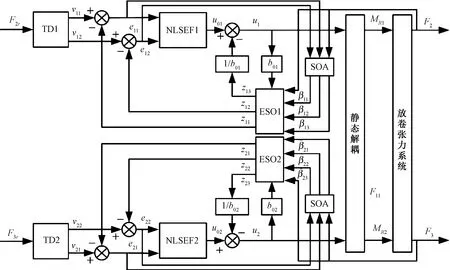
圖2 人群搜索自抗擾控制器結構圖

具體自抗擾控制算法表示如下：

(9)

式中：ui為擾動補償量；ri為過渡快慢因子；h為積分步長；βi1、βi2、βi3為ESO調節參數；kip與kid為NLSEF調節參數；k為離散數；ei為張力估計誤差。

fal(e,α,δ)函數為：

(10)

fhan(x1,x2,r,h)最速控制綜合函數為：

(11)

2.2 人群搜索算法

人群搜索算法是將人群內每個個體隨機搜索行為歸納起來，通過模擬人的智能搜索行為，使個體加入到智能搜索中，并結合個體各方面的社會行為確定搜索步長與方向，經位置更新得到最優解。

人群搜索算法通過適應度值對個體或解進行優選并對其進行位置更新，使其不斷地向最優解方向進行優化。選取最小目標函數為時間乘以絕對誤差積分函數，并加入u2(t)預防產生過大的震蕩調整，則目標函數為：

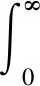
(12)

式中：c1、c2分別為誤差和控制輸出平方項的權值；e(t)為初始值與輸出間的誤差；u(t)為控制器輸出。

為了保證系統穩定運行，結合懲罰控制來預防發生超調，則最優指標為：

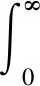
(13)

式中：取權值c1=0.998；c2=0.002；c3=100。

采用不確定推理的模糊邏輯得到搜索步長αij為：

(14)

其參數為：

(15)

式中：uij為j維搜索空間目標值i隸屬度；δij為高斯隸屬函數參數；c為慣性權值。

對搜索者利己方向di,ego、利他方向di,alt和預動方向di,pro分析得式(16)：

(16)

通過隨機加權、幾何平均，將所獲取各方向進行分配組合，得到搜索方向為：

dij(t)=sign(ωdij,pro+φ1dij,ego+φ2dij,alt)

(17)

式中：xi(t1)、xi(t2)為{xi(t-2),xi(t-1),xi(t)}內最優位置；pi,best為第i個搜索個體到當前通過的最優位置；gi,best為第i個搜索個體所在鄰域的全體最優位置。

通過得到的搜索步長和方向，建立搜索個體位置更新，見式(18)：

(18)

3 仿真分析

為了驗證人群搜索自抗擾(SOA-ADRC)控制器在解耦和抗干擾方面的控制性能，構建放卷系統模型和SOA-ADRC控制器模型，并與PID控制器進行仿真實驗分析。放卷系統數學模型參數見表1，控制器參數見表2。

3.1 解耦仿真分析

由放卷張力系統模型分析，放卷部分與牽引部分的張力存在耦合性。當放卷半徑R1為0.2 m、輥筒角速度ω3為100 r/min時，放卷系統張力F2在4 s時由40 N階躍升高到45 N，6 s時由45 N階躍降低到40 N。圖3為解耦性能仿真曲線。可以看出，在人群搜索自抗擾控制下，張力F2在4～6 s發生5 N波動時，張力F3基本未發生波動，而在PID控制時，張力F2波動時，F3發生0.75 N波動。因此表明人群搜索自抗擾控制器能夠實現良好的解耦控制，而PID控制器不能實現較好的解耦控制。

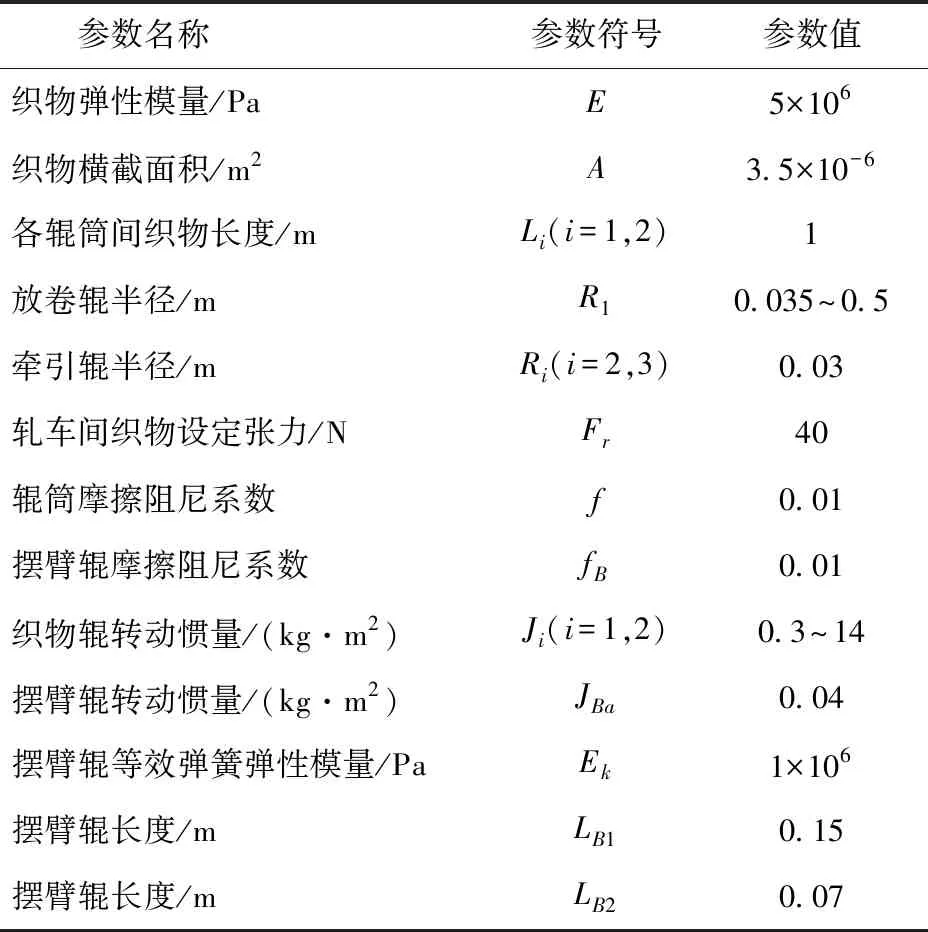
表1 放卷系統數學模型參數

表2 控制器參數

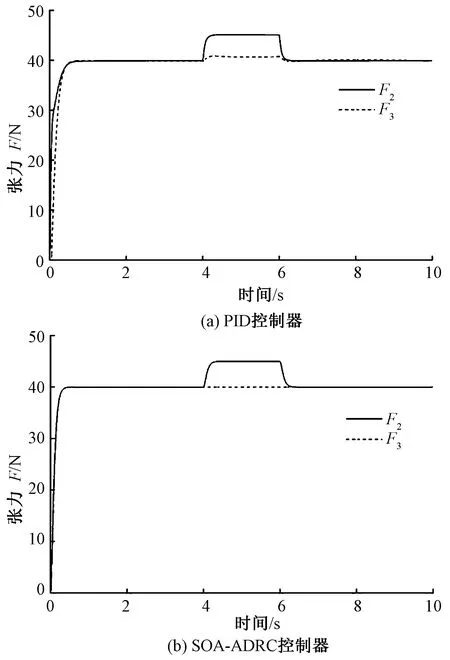
圖3 解耦性能仿真曲線

3.2 抗參數擾動仿真分析

當ω3為100 r/min，R1依次為0.20、0.15、0.10 m時，在PID與人群搜索自抗擾控制器對張力F2的控制效果下，R1變動時F2仿真曲線見圖4。

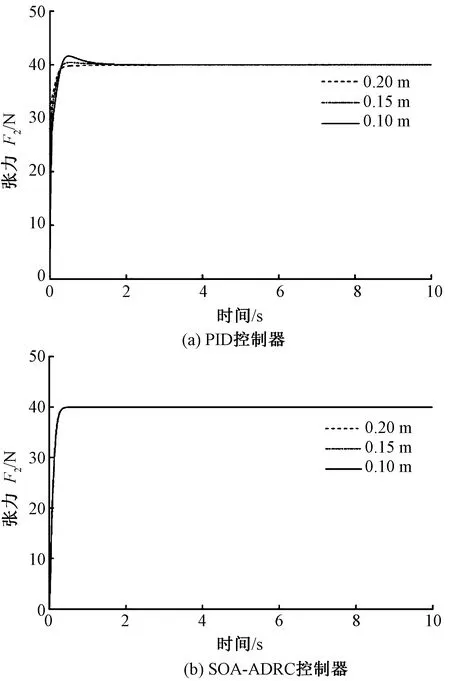
圖4 R1變動時F2仿真曲線

由圖4可以看出，在放卷半徑逐漸減小時，采用人群搜索自抗擾控制，張力F2并不隨著卷徑的變化而變化，基本保持穩定；而采用PID控制時，張力F2達到穩定運行的時間變長，并有4.6%的超調量。因此說明人群搜索自抗擾控制器能有效抑制放卷輥半徑變化引起的張力波動，比PID控制器有較好的抗參數擾動性能。

當R1為0.2 m，ω3為100、150、200 r/min時，在PID與人群搜索自抗擾控制器對張力F3的控制效果下，ω3變動時F3仿真曲線見圖5。可以看出，當軋染機輥筒3的角速度ω3逐漸變大時，張力F3采用PID控制時達到穩定運行的時間變長，并有7.4%的超調量，但在人群搜索自抗擾控制下，織物張力F3并不會隨著速度的變化而變化，基本不發生波動，并且達到穩態的時間也更快。說明人群搜索自抗擾控制器能有效抑制放卷張力系統內部參數不斷變化引起的張力波動，比PID控制器有較好的抑制參數擾動性能。

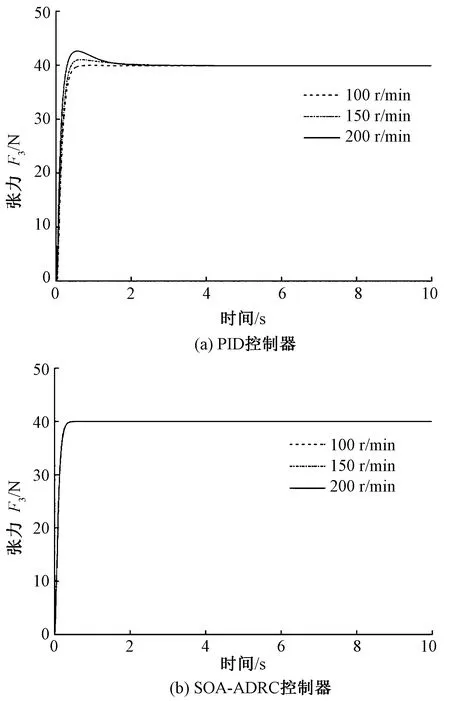
圖5 ω3變動時F3仿真曲線

3.3 抗外部干擾性仿真分析

由于放卷張力系統容易受到外界條件的影響，因此，在放卷張力系統中加入正弦擾動和噪聲信號作為未知的干擾。在PID和人群搜索自抗擾控制器對放卷張力的控制效果下，外部干擾時F2的仿真曲線見圖6。

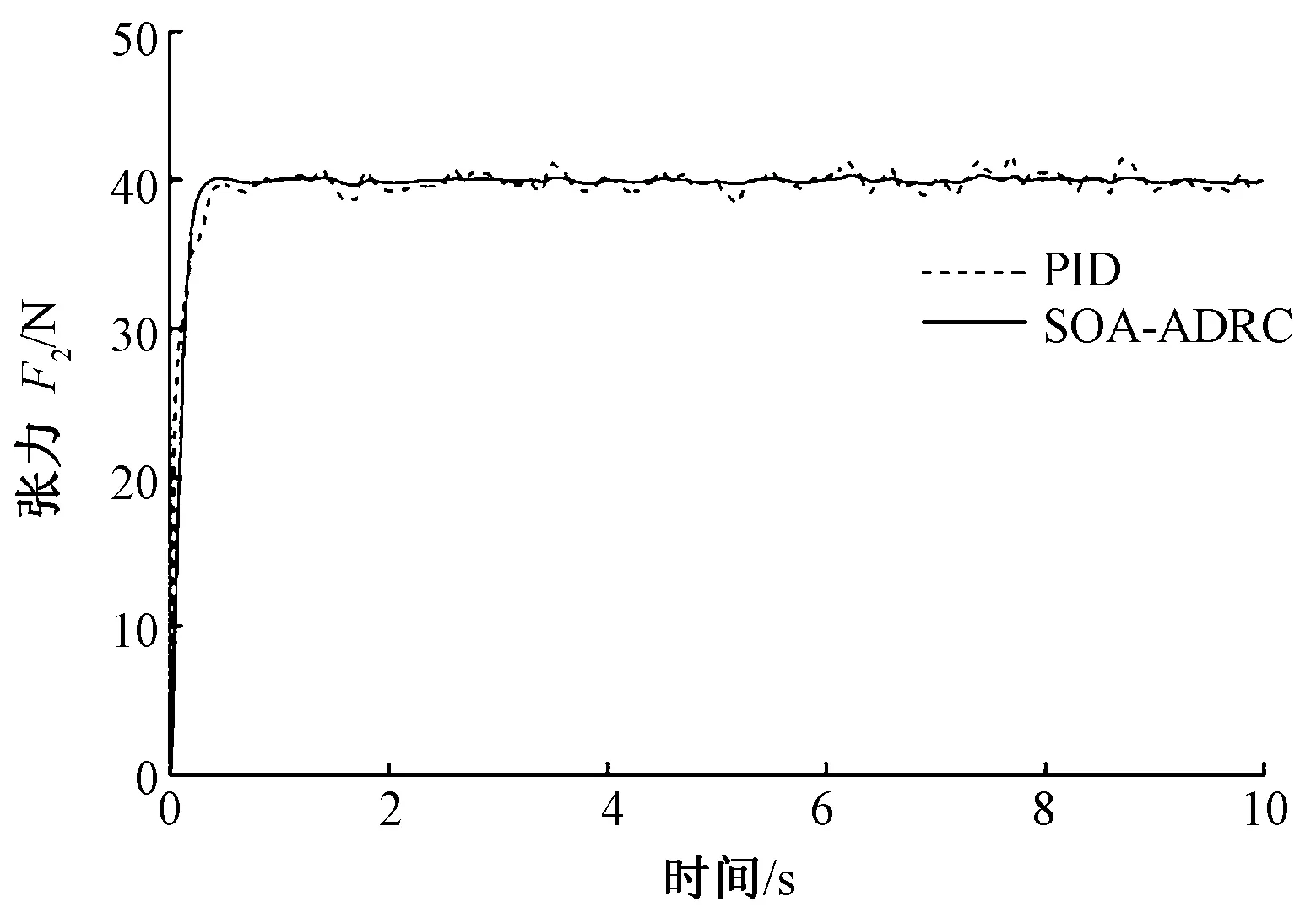
圖6 外部干擾時F2的仿真曲線

由圖6可以看出，當系統受到外部因素干擾時，張力F2采用PID控制時出現劇烈的波動，影響系統的穩定運行，而采用人群搜索自抗擾控制時產生波動很小，可以使系統保持穩定，說明人群搜索自抗擾控制器有較好的抗外部干擾效果。

4 結束語

本文提出人群搜索自抗擾控制的方法，將其應用于控制系統張力的波動，使軋染機放卷張力系統控制達到穩定運行的要求。仿真實驗得出，在放卷張力系統的解耦和抗干擾性能方面，人群搜索自抗擾控制比PID控制具有更好的張力控制效果，實現了放卷張力系統的穩定運行，使軋染機可以更好地適應復雜的生產加工工藝要求。