無缺陷退貨下基于零售商銷售努力競爭的供應鏈協調研究

胡博雅，樊相宇，武小平 HU Boya， FAN Xiangyu， WU Xiaoping

（1. 西安郵電大學 經濟管理學院，陜西 西安710061；2. 西安郵電大學 現代郵政學院，陜西 西安710061）

0 引 言

隨著經濟的高速發展，現在的供應商常常通過多個零售商進行產品的銷售。但是這種情況下，銷售價格通常是固定的，而影響需求的因素更主要的是不同零售商的銷售努力。零售商可以通過提高銷售努力，在銷售前中后期投入更多的資源，引導需求發生變化。在市場研究領域也有學者考慮到市場競爭不僅受價格影響，還存在銷售努力等方面的競爭。Hall J 等[1]研究了存在價格與服務水平競爭時的供應鏈協調問題，并提出了相應建議。馬利軍等[2]研究了多零售商間的銷售努力水平競爭以及相應的供應鏈協調問題。龐慶華等[3]研究了兩個零售商存在信用及努力水平競爭時的供應鏈協調問題。范小軍等[4]同時考慮了價格與服務競爭，提出組合定價策略實現整體渠道協調。王道平等[5]在考慮零售商促銷努力競爭的基礎上，對比分析促銷努力成本信息對稱和非對稱的情形，提出使零售商傳遞真實的促銷努力成本信息的轉移支付契約。陳佳佳等[6]建立了基于努力水平競爭的供應鏈網絡均衡模型，研究努力水平對銷量及利潤的影響。

在高度競爭的市場環境下，為了吸引顧客，企業對顧客退貨的規定變得越發寬松，即使產品不存在功能或外觀缺陷，企業也允許顧客在購買后的一段時間內退貨，即無缺陷退貨（False Failure Returns）。產品的無缺陷退貨可能由于產品未達消費者預期，消費者對產品使用功能不了解，消費者后悔等多種原因造成。大量的無缺陷退貨會給企業帶來巨大的成本損失。目前，已有學者對存在無缺陷退貨的供應鏈協調問題進行研究。Zhang X 等[7]為降低無缺陷退貨率，設計了雙邊道德風險下收益共享合同協調供應鏈。姚澤有[8]研究在銷售努力水平及退貨價格影響需求時，通過回饋與懲罰契約實現易逝品供應鏈的協調。Wei F等[9]研究了數量折扣合同，以促使零售商減少無缺陷退貨，實現供應鏈的協調。徐慧等[10]構建了與價格及銷售努力相關的存在顧客退貨的供應鏈模型，設計回購契約協調供應鏈，使供應商與零售商實現共贏。劉秋生等[11]研究分析發現單純的回購合同不能達到供應鏈協調，提出了限制性回購契約，通過限制回購產品數量來協調供應鏈。李明芳等[12]提出通過雙向激勵契約，激勵制造商與零售商服務投入，以減少無缺陷退貨量。張立韜等[13]運用了CVaR 方法研究了促銷努力影響需求下的退貨政策，引入成本分擔機制協調供應鏈。

可以發現上述研究存在無缺陷退貨的供應鏈協調問題，大多只考慮存在一個供應商和一個零售商的簡單供應鏈。而現實市場環境中，往往會有更加復雜的供應鏈結構。本文考慮零售商間存在銷售努力水平競爭的供應鏈協調問題，基于零售商銷售努力水平同時影響市場需求與無缺陷退貨率時，對存在無缺陷退貨的供應鏈進行研究，設計回饋與懲罰契約，以實現供應鏈的協調。

1 問題描述與假設

1.1 問題描述

本文以一個供應商和兩個存在銷售努力水平競爭的零售商構成的二級供應鏈為研究對象（如圖1 所示）。供應商生產某種產品并提供給兩零售商進行銷售，只考慮單期銷售。為了提高市場需求，銷售期內消費者可以全額無缺陷退貨。

1.2 假設與符號說明

為了使本論文的研究問題更具體，故針對模型提出以下假設：

假設1：供應商與零售商之間存在Stackelberg 博弈，領導者為供應商，追隨者為零售商，兩個零售商具有相同競爭能力，都只進行一次訂貨；

假設2：無缺陷退貨為全額退貨，且無缺陷退貨產品不能在單期內再次銷售；

假設3：零售商面臨的市場需求不僅與自身銷售努力水平相關，還與零售商之間的競爭敏感系數相關；假設4：不考慮產能約束，即供應商能滿足兩零售商訂購量；

假設5：供應鏈各成員都是完全理想和風險中性的，且彼此信息完全；

符號說明如下：

為了表達的簡潔和求解的明了，在此說明一些符號的運算規則：

p：單位銷售價格；w：單位批發價格；c：單位生產成本；

m：零售商處理單位無缺陷退貨產品成本；

s：銷售季節結束后無缺陷退貨產品的單位殘余價值；ei：零售商提供的銷售努力水平；g ei（）：零售商i的銷售努力水平為ei時的努力成本，g ei（）=ηe2/2；h ei（）：零售商i的銷售努力水平為ei時的無缺陷退貨率；

h ei（）=θ-φei，θ 表示零售商維持最低銷售服務水平消費者的無缺陷退貨率；

φ 為服務退貨系數，表示消費者無缺陷退貨率對零售商銷售服務水平的敏感度。

零售商i面臨是市場需求為：

Di=α+λei-βej，i=1，2，j=3-i

其中：

α：零售商i（i=1 ，2 ）的確定性需求基數；

λ：市場需求對零售商努力水平的敏感系數；

β：市場需求對零售商i i=1，（ ）2 努力水平競爭的敏感系數，反映競爭的激烈程度。

針對以上參數，基于理性約束條件如下：

2 模型建立與分析

2.1 集中決策模型

集中決策下，供應商與零售商共同協作以使供應鏈整體達到最優狀態。即供應商與兩零售商協作，要決定的決策變量為競爭零售商的銷售努力水平。

供應鏈系統的利潤函數為：

分別對式（1） 求ei和ej的偏導數得：

進一步求二階偏導有：

函數的海塞矩陣：

2.2 分散決策模型

分散式供應鏈中，供應商與零售商由于分屬于不同的企業，他們分散獨立決策，各自以自身利益最大化決策。供應商與兩零售商存在Stackelberg 博弈，博弈過程中供應商處于強勢主導地位，零售商處于跟隨地位。兩個零售商之間為Nash 博弈。

模型中事件發生及博弈決策的順序如下：

（1） 銷售季節開始前，兩零售商根據批發價格和市場銷售價格，同時進行自身銷售努力水平及訂貨量決策，以最大化自身的收益；

（2） 零售商向供應商訂購產品，供應商滿足訂單；

（3） 兩零售商滿足顧客需求，同時接受顧客無缺陷退貨；

銷售期內供應商的利潤函數為：

銷售期內兩競爭零售商的利潤函數為：

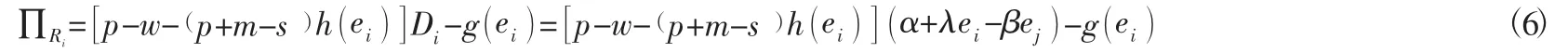
對式（6） 中ei分別求一階偏導得：

在分散決策下，兩個零售商的最優銷售努力水平都相等，并且通過式（4） 可知，集中決策下兩者也是相等的。因此在兩個零售商和供應商構成的兩級供應鏈下，無論是采取集中決策和分散決策，零售商取得最優收益的必要條件就是市場產品的銷售努力水平需統一。

2.3 基于回饋與懲罰契約協調策略模型

集中決策是一種理想的狀態，實際情況中存在的基本上都是分散決策模型。根據以往學者的研究，要使分散決策供應鏈整體達到協調的條件為，分散決策下零售商的訂貨量達到集中決策下零售商的訂貨量。

由此提出回饋與懲罰契約，供應商給兩零售商提供一個銷售目標H，對于銷售量高于H的部分，給予單位產品獎勵k，對于銷售量低于H的部分，給予單位產品懲罰k。從而有效刺激零售商銷售努力水平和訂貨量的增加，消除“雙重邊際化”效應，增加整個供應鏈的收益。

在基于回饋與懲罰契約下銷售期內零售商的利潤函數為：

供應商的利潤函數為：

對式（10） 求一階偏導得：

此時零售商的最優努力水平滿足：

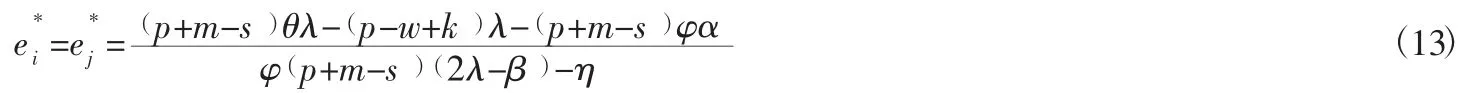
為了供應商和零售商都能接受此契約，協調后的各成員利潤不低于分散決策中各自的利潤。即要滿足以下參與約束條件：

由此求得：

即當kH滿足式（16） 時，供應鏈的協調就是有效的，保證了零售商和供應商的參與約束條件得到滿足，從而上述（k，H）保證了契約是Pareto 改進的。

3 算例分析

由于本文變量較多，為了進一步驗證契約的合理性，利用Matlab 對上述模型進行數值算例分析，給出直觀的結果。

某行業中一上游處于領導者的供應商生產一種產品，將自己的產品同時提供給兩個零售商進行銷售。但是由于為確保產品自身市場占有、品牌價值等因素，供應商確定單位批發價格和銷售價格，兩零售商以銷售努力競爭影響市場需求。為刺激需求，零售商接受顧客全額無缺陷退貨。零售商自身銷售努力同時影響無缺陷退貨率。

假設相關參數取值如表1 所示：

表1 相關參數賦值

由式（14） 得出回饋與懲罰契約參數k=9.852，因此，根據式（16） 可得209.53≤H≤214.93，這里假定H=210。

對集中式決策、分散式決策以及采用回饋與懲罰契約對供應鏈進行協調后的決策結果、供應鏈成員利潤以及供應鏈整體利潤進行了比較，得出的結果如表2、表3 所示：

表2 不同模式下的決策結果、供應鏈成員及整體利潤比較

表3 努力水平敏感系數及競爭敏感系數對各成員和系統利潤的影響

根據表2 和表3 可知：

（1） 引入回饋與懲罰契約，在參數滿足一定條件的情況下，可以使分散決策下供應鏈總利潤達到集中決策下總利潤，實現供應鏈協調。

（2） 兩零售商的利潤隨自身努力水平敏感系數λ 的增大而增大，隨競爭敏感系數β 的減小而增大。這表明零售商可以通過增大自身的努力水平敏感系數來獲取更多的利潤。

（3） 供應鏈及成員利潤隨λ 的增大而減小，隨β 的減小而增大，這表明可以通過調整兩競爭零售商的努力水平敏感系數和競爭敏感系數的值，使供應鏈利潤增加更多。

4 結 論

本文研究了存在零售商銷售努力競爭和無缺陷退貨的供應鏈的協調問題。探究市場需求和無缺陷退貨同時受零售商銷售努力的影響下，分析集中決策與分散決策下零售商的最優努力水平與最優訂貨量。設計一種回饋與懲罰契約，實現供應鏈協調達到帕累托改進，并通過數值算例分析了協調的有效性與參數的取值范圍及敏感系數對供應鏈利潤的影響。通過研究可知，零售商競爭時最優努力水平與零售商自身敏感系數成正比，與競爭敏感系數成反比。供應商可以在一定范圍內通過調整銷售目標控制供應鏈成員利潤分配，使自己與零售商的利潤均大于無契約時的利潤，與零售商實現共贏。本文研究對存在無缺陷退貨的供應鏈決策提供了理論依據，但也存在著一定的不足。現實市場供應鏈中，供應鏈成員大多存在著信息非對稱的情況，以后可以從供應鏈成員信息非對稱方面擴展本研究。