聯結經驗：創新背景下統計學教學的一點思考

陳玲菊 謝碧華

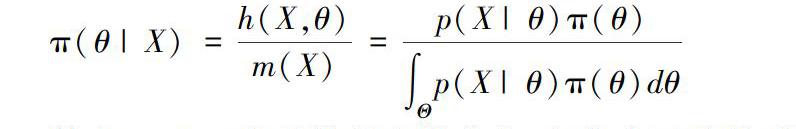
【摘要】在大數據時代，統計學與多學科的相互滲透使得傳統的簡單性教學原則的局限性逐漸顯現出來.本文是在法國當代思想家埃德加·莫蘭（Edgar Morin）所提倡的復雜性科學視野下，討論用聯結經驗的方法進行統計學教學的一點思考.

【關鍵詞】統計;創新;聯結;經驗;腦科學

【基金項目】福建省中青年教師教育和科研項目.基金號：JAT160383.

一、引 言

如何在課堂上行之有效的教學？從美國心理學家約翰·華生（John Broadus Watson）創立了行為主義學習理論以來，在格思里、赫爾、斯金納等的影響下，行為主義學習理論在美國占據主導地位長達半個世紀之久.行為主義者認為，學習是刺激與反應之間的聯結，他們的基本假設是：行為是學習者對環境刺激所做出的反應.他們把環境看成刺激，把伴隨的有機體行為看作反應，認為所有行為都是習得的.行為主義學習理論應用在學校教育實踐上，就是要求教師掌握塑造和矯正學生行為的方法，在最大限度上強化學生的合適行為，消除不合適行為.對教育而言，這種建立在刺激與反應聯結上的教學模式，只強調外部刺激而完全忽視學習者的內部心理過程，忽略了人腦的認知行為與動物的區別，訓練雖然可以調整人的行為反應，但卻忽略了人們對未來意外事件的理解力.隨著腦科學中有關人的高級認知機制研究成果的呈現及人們對學習本質的認識的不斷深入，以創設網絡式聯結為導向、基于情境學習和情境認知的理論研究和實踐模式的開發越來越受到心理學、人工智能、人類學等領域研究者的關注.

腦研究表明人的大腦是個并行處理器.在學習中，人腦會對有意義和無意義的信息與場景做出不同的反應.僅存在于記憶中的事實沒有意義，但當事實與復雜卻熟悉的經驗聯系起來時就產生了意義，這樣，新的信息就與我們已經知道和掌握的信息聯系在一起了.人腦復雜的模式化核心特征對教學提出：優秀的教師不只是為測試而教.而是會利用學生帶到班上的背景和信息來展開教學，這些背景與信息包括他們與家長的經驗、力量和愛.在學習過程中，學生能更好地領悟他們自己和生活，浸潤在學科當中，其經驗的拓展和心理的升華也隨之開始.對于統計學這門與人們的日常生活息息相關的學科，如何在教學中利用聯結將統計的方法和思想“編排”到學生對已有客觀世界的體驗中？如何恰如其分地結合一些實驗和例子將統計學內化為世界觀和方法論？如何培養學生運用統計學的思想方法發現問題、分析問題和解決問題的能力？這是當今社會對創新人才日益高漲的需求下，每一位任課教師所要思考的問題.

傳統的數學教學方法，往往只滿足于對定理、公式的陳述與證明，以及對技巧的應用，照搬課本內容.這樣容易造成數學孤立于生活經驗，與現實失去聯結，完全變成了冰冷冷的教條.這種教學實際上是過分強調記憶——對定義、公式和定理或者是對解題技巧的記憶.在這種教學方式下，學生失去了主體地位，只是被動地吸收、消化，學習興趣不高，沒有積極性，更談不上知識的創新與運用.關于統計的教學方法，已經有很多討論，比如案例教學、“辨誤”教學、啟發教學、討論教學，這些方法為統計教學的改革和創新提供了寶貴的參考.但是鮮有具體討論如何利用聯結進行創新性教學的嘗試.事實上，從約翰·格蘭特（John Graunt）清點倫敦的死亡人數，建立人類歷史上第一張死亡表開始，統計的方法與理論就在為人們提供便利，并在解決生活中的實際問題中不斷發展.教材中所呈現的定義、公式和定理是眾學者在幾百年來對客觀世界的觀察、體驗的基礎上抽象出來的套裝知識，每個定義、公式和定理都有其產生背景及在現實中的應用.因此，改進教學方法的首要任務就是設計編排課堂的教學內容.教學不僅要講定義、公式、定理，還要適當地引入背景知識，從而將教材中的套裝知識與學生的主體經驗聯結在一起，盡可能地將教材中冰冷冷的知識骨架轉化為有血有肉的、被學生所喜聞樂見的形象.這樣能夠激起學生的興趣，并為進一步引導學生運用統計的思想方法去發現、思考、解決身邊或社會上的問題打下基礎.接下來，結合多年教學實踐，筆者總結了教學中常用的幾個例子，希望為廣大同仁提供參考借鑒.

二、案 例

首先，統計有什么用？我們可以引入一個古老的寓言故事：在非洲草原上如果見到羚羊在奔跑，那一定是獅子來了;如果見到獅子在躲避，那就是象群發怒了;如果見到成百上千的獅子和大象集體逃命的壯觀景象，那是——螞蟻軍團來了！

這個寓言實際上就蘊含著統計推理的基本過程：觀察現象——做出推斷.統計中的觀察是通過試驗收集和分析數據（觀察現象），從而對研究對象的客觀規律做出合理的估計和判斷.

1.隨機抽樣

隨機抽樣在日常生活中隨處可見，如看看餃子是否煮熟了，就隨便撈一個嘗嘗，這就是隨機抽樣.在隨機抽樣中，樣本的抽取要滿足隨機性，否則，將影響試驗結果的客觀性，從而導致試驗失敗.比如美國的蓋洛普民意調查機構，其創始人喬治·蓋洛普在1932年成功地預測出其岳母將在州政府秘書的競選中獲勝.接著在1936年及其后的兩次總統選舉中都正確地預測出獲勝的一方.但是在1948年的總統選舉中，對誰將接任羅斯福成為下一任總統時，基于50000人次的調查，預測杜威獲勝.但實際結果是杜魯門獲勝.民意測驗出了什么問題？真實情況是，1948年的民意調查訪問人員選擇了過多的共和黨人.這是因為共和黨人較為富裕，受過較好的教育，住在較好的街區，較易接受訪問，所以訪問人員喜歡采訪共和黨人，這就造成了民意測驗中偏向共和黨的現象.

現在，蓋洛普民意測驗仍然享譽全球.在蓋洛普民意測驗中出現非常頻繁的問題有：誰是最受人們贊美的人？男人是否會選擇健康又美麗的女人？而蓋洛普民意測驗中最熱門的十大問題是：為什么人生在世會有患難？是否有一種方法可以醫治所有的疾病？世界上為什么有罪惡的存在？人類會迎來永久的和平嗎？人與人之間會彼此相愛嗎？世界末日何時來臨？我和自己的家庭能有什么樣的未來？人死后還有生命嗎？天國會是什么樣子？我怎樣才能成為一個更加淳樸高尚的人？

抽樣調查問題的核心便是抽樣，抽樣的原理很簡單，但是很多“謊言”就是出自看似簡單的抽樣.比如曾經在美國的《時代周刊》上有這么一條信息：1924級的耶魯畢業生平均年收入有25111美元.這在當時可是絕對的高收入了.那么，我們是馬上驚呼耶魯畢業生真棒，還是應該質疑一下它的真實性呢？它的調查樣本是什么？經過了半個世紀他們能找到所有1924級的耶魯畢業生嗎？或許只是用了抽樣調查.那么它的這個抽樣調查是真的具有代表性嗎？它能聯系到的只是那些功成名就的畢業生吧，那些在畢業生通訊錄上被注明“地址不詳”的迷路小羔羊呢？就算它的抽樣具有一定的代表性，那么所有接受調查的畢業生，說的都是真話嗎？會不會因為虛榮或是逃稅而說假話？即便這所有都是真的，那么這個收入平均數的類型是什么？是均數、中位數還是眾數？

在數據泛濫的時代，真實的信息與噪音同時存在，我們要學會運用統計學的思想方法進行分析思考，去偽存真，分辨出其中隱藏的謬誤之處，從而更加客觀地認識我們所處的世界.再比如“辛普森悖論”：英國統計學家辛普森（E.H.Simpson）在1951年發表的論文中指出，在某些情況下，在分組比較中占優勢的一方，可能在合并后的總評中成為失勢的一方.比如：1991年美國航空協會收集阿拉斯加航空和西美航空飛經5個機場的誤點數據如下表.

阿拉斯加航空在所有5個機場都更為準點，但總體上卻是西美航空公司更為準點！類似的問題還可能出現在學校招生比例、職場的錄取率等問題中.辛普森悖論被人們稱為是“投向統計學的炸彈”，無可挑剔卻讓人難以接受.然而探究其數學實質，不難發現，其詭異的外表下，內部卻十分簡單：

分數ba>fe，dc>hg，但分數b+da+c未必大于f+he+g.

這就告訴我們對于總體現象，要仔細研究細節，不要輕易下結論.

2.假設檢驗思想與貝葉斯理論

假設檢驗的基本思想是依據概率論中的小概率原理，應用概率反證法，通過觀察小概率事件是否發生來判別關于總體的假設是否正確.小概率的事件在一次試驗中幾乎不可能發生，如果真的發生了，那么我們就認為原假設值得懷疑.關于這個思想可以引入一個古代的故事：

魏晉名士王戎七歲的時候，曾經和其他小朋友一起出去玩，路邊一棵李子樹上結滿了李子，多到把樹枝都壓彎了.許多小朋友爭相跑去摘李子，只有王戎不動.有人問他為什么，他說：“這李子樹就長在路邊卻結了那么多果實，其果實必定是苦的.”后來別人摘來果實一嘗，果然如此.

在這個故事中，王戎就引用了概率反證法.假設路邊的李子是甜的，那么樹上有這么多李子應該是小概率事件，既然小概率事件發生了（即李子多到把樹枝都壓彎了），那么就懷疑原假設，即認為李子是苦的.

統計中的假設檢驗利用的就是概率反證法.關于假設檢驗的方法，《女士品茶》一書中有這樣的例子：在英國劍橋一個夏日的午后，一群大學的紳士和他們的夫人們，還有來訪者，正圍坐在戶外的桌旁，享用著下午茶.在品茶過程中，一位女士說：“奶茶是先放紅茶還是先放牛奶，味道完全不一樣，我一下子就能品嘗出來”.在場的一幫科學精英們對這位女士的“胡言亂語”嗤之以鼻.這怎么可能呢？他們不能想象，僅僅因為加茶加奶的先后順序不同，茶就會發生不同的化學反應嗎？然而，這個問題引起了在座的一位先生的興趣.他提議做一項試驗來檢驗如下假設是否可以接受.

假設：該女士無此種鑒別能力.

他在女士看不到的地方準備了10杯分別利用兩種方法沖泡的奶茶.結果那位女士竟然正確地分辨出每一杯的沖泡順序，那么我們是否拒絕假設呢？這位先生的想法是：如果假設是真的.那么，每次猜對的概率都是0.5，10次都猜對的概率是2-10，顯然是小概率.小概率事件發生了，于是拒絕原假設，即認為該女士有此種鑒別能力.

在生活中，對小概率問題人們一般不會擔心.“杞人憂天”就是將普遍共識是小概率的事件的概率放大的結果.實際上，由于每個人都有自己的信仰和偏見，所以對事件發生的概率的估計各不相同，這些估計與客觀概率的差距大小不一.貝葉斯理論告訴我們，盡管我們的信念使我們對事件的預測永遠做不到完全客觀、合理或是準確.不過，我們可以不斷收集證據，一步步調整對事件的預測，使之一步步靠近事件的真相.我們可以簡要地描述一下貝葉斯理論：對于事件A，假設我們原來認為它發生的概率為P（A），如果我們觀察到事件B，那么在事件B的基礎上，我們可以將事件A發生的概率調整為：

P（A|B）=P（B|A）P（A）P（B|A）P（A）+P（B|A）P（A）

其中，P（B|A）為在事件A發生的條件下事件B發生的概率，P（B|A）為在事件A沒發生的條件下事件B發生的概率.一般地，我們稱P（A）為先驗概率，而在事件B基礎上調整得到的概率P（A|B）為后驗概率.

實際上，貝葉斯理論當初是用來表達貝葉斯的哲學觀：上帝是完美的，他創造自然是有章可循的，我們可以通過近似值一點點地模擬并認識宇宙.收集的證據越多，就越接近真相.貝葉斯的朋友在向眾人呈現《機會的學說概論》時舉了一個“人”的例子：作為第一個出現在這個世界的人，第一次看見日出時并不知道日出是必然還是偶然現象.然而隨著日后每一天的日出，他信心一步步增強，直到最后他預測每天太陽升起的概率是100%.

再比如美國的“9.11”恐怖襲擊事件.2001年9月11日清晨，當人們從夢中醒來時，大部分人都想不到恐怖分子的飛機會撞向曼哈頓世貿中心大樓.但是，世貿中心第一次遭受襲擊后，人們才意識到這也許是一次恐怖襲擊.直到第二座高樓被襲擊之后，人們才相信確實遭遇了恐怖襲擊.

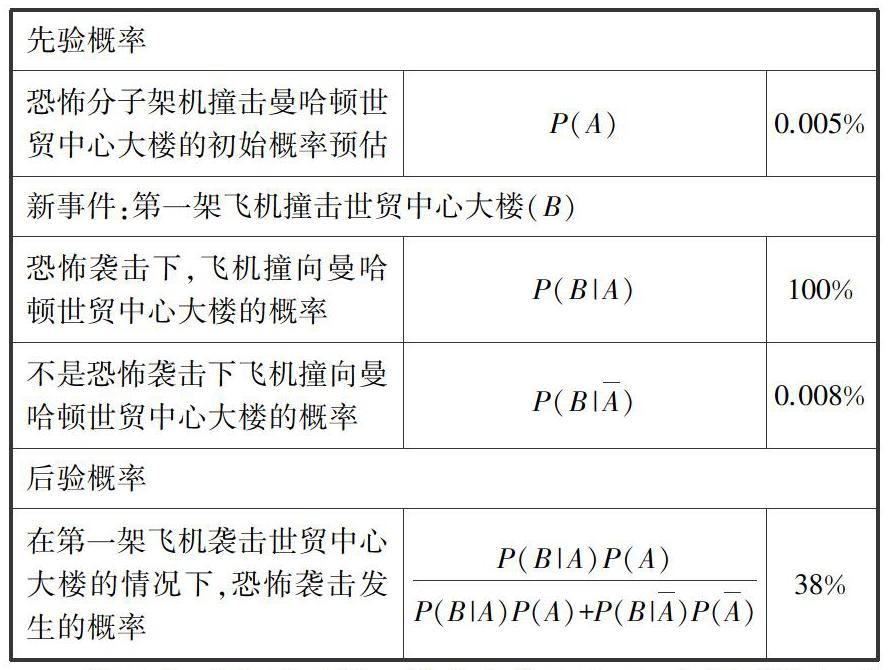
貝葉斯定理可以解釋這一過程.比如，在第一架飛機撞擊大樓之前，我們預測曼哈頓的高樓遭遇飛機撞擊的概率只有1：20000或0.005%.當然，我們還是會認為世貿中心意外遭遇飛機撞擊的概率是非常低的.人們靠經驗也能準確地預測出0.005%這個數字：9月11日之前的25000天，雖然一直有飛機盤旋在曼哈頓的上空，但是只發生了兩次這樣的意外事故：一次是1945年的美國帝國大廈事件，另一次是1946年的川普大廈事件.這樣看來，此類意外事故發生的概率只有1∶12500.在第一架飛機撞上世貿中心大樓的那一刻，用貝葉斯定理計算（見表），發生飛機撞擊事件的概率便會從0.005%劇增致38%.

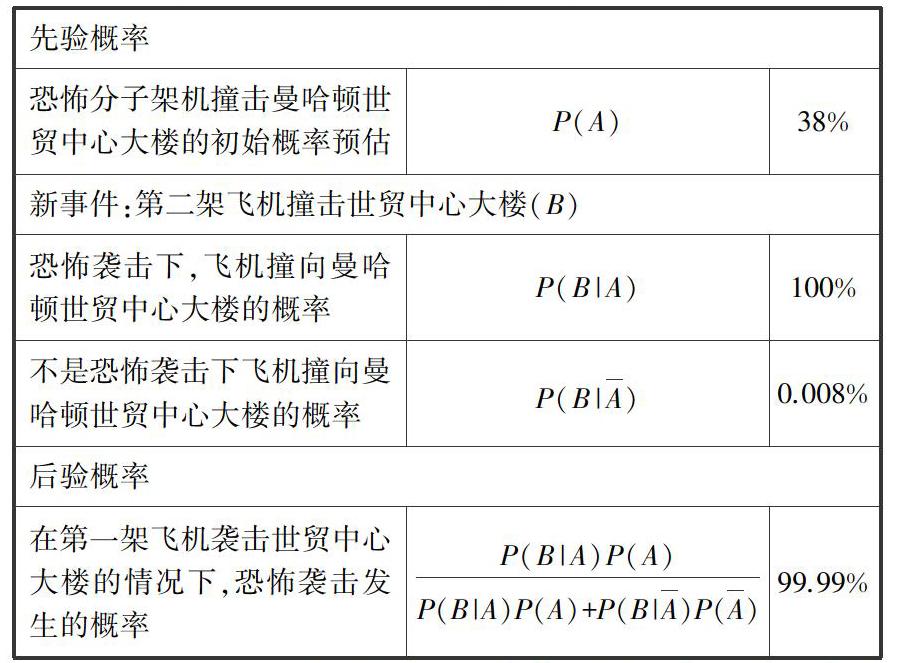
接下來，我們看看第二次襲擊發生之后，由貝葉斯定理得到的遭遇襲擊的概率會變為多少.這次，38%是先驗概率.這時根據貝葉斯定理得到的遭遇恐怖襲擊的概率就變成了99.99%，這就表示恐怖襲擊一定會發生！

先驗概率恐怖分子架機撞擊曼哈頓世貿中心大樓的初始概率預估P（A）38%

新事件：第二架飛機撞擊世貿中心大樓（B）恐怖襲擊下，飛機撞向曼哈頓世貿中心大樓的概率P（B|A）100%不是恐怖襲擊下飛機撞向曼哈頓世貿中心大樓的概率P（B|A）0.008%后驗概率在第一架飛機襲擊世貿中心大樓的情況下，恐怖襲擊發生的概率P（B|A）P（A）P（B|A）P（A）+P（B|A）P（A）99.99%

美國的烏爾加利斯作為當今世界頂級的賭徒就是成功利用貝葉斯定理的一個很好的范例.他特別喜歡看NBA比賽并投注.每年從11月至下一年6月，烏爾加利斯每晚都會觀看NBA，每次看5場，分別由5臺電視機同時播放.事實上，幾乎所有的NBA比賽他都看過——不論是直播還是錄播.除此之外，他還經營著一家球探服務機構（本質上來說其實是為他自己服務的），雇用了一些助手，讓這些助手將每個球員在每場比賽中的防守陣形繪制成圖，這種做法給烏爾加利斯帶來的好處就連很多NBA球隊都望塵莫及.他關注了幾十名球員的微博，仔細查看每140個字符的微博內容，試圖從中找出關聯信息：若某位球員在微博上說自己那晚晚些時候會去某個夜總會，則這位球員的心思很可能根本就沒在比賽上.他也很關注球隊教練在新聞發布會上說的話，比如，如果某位教練說，他希望他的隊伍“學習進攻”或者“練好籃球基本功”，那可能表明他希望放慢比賽的節奏.

烏爾加利斯靠著這些小秘密，即使年景比較差的時候也能賺上100萬美元，年景好的時候，可以賺上三四百萬美元.他的成功就是建立在貝葉斯思維上的，不斷尋找證據，那么你的預測會越來越接近客觀現實.這種思想反映在參數估計里，就形成了貝葉斯估計方法：在已知總體分布的情況下，貝葉斯學派認為待估參數θ可以看作隨機變量，在得到新的樣本信息之前，人們對θ的認知是先驗分布π（θ），在得到新的樣本信息X后，人們對θ的認知為π（θ|X），稱為后驗分布，它的計算公式是：

π（θ|X）=h（X，θ）m（X）=p（X|θ）π（θ）∫Θp（X|θ）π（θ）dθ

其中p（X|θ）為總體的條件分布，它集中了總體、樣本和先驗中有關θ的一切信息.其計算公式就是用密度函數表示的貝葉斯公式.由此得到的后驗分布π（θ|X）是用總體和樣本對先驗分布做出的調整方法，要比π（θ）更接近θ的實際情況.

綜合起來看，則好比是人類剛開始時對大自然只有少得可憐的先驗知識，但隨著不斷的觀察、實驗獲得更多的樣本、結果，人們對自然界的規律摸得越來越透徹.所以，貝葉斯方法既符合人們日常生活的思考方式，也符合人們認識自然的規律，因而經過不斷的發展，最終占據統計學領域的半壁江山，與經典統計學分庭抗禮.

法國當代思想家埃德加·莫蘭（Edgar Morin）寫的《未來教育所必需的七種知識》指出，教育的一個黑洞就是人們教授確定性，然而需要教授的恰恰是不確定性.今天，所有偉大的科學，從微觀物理學到人類進化學都成為確定性和不確定性之間的賭博.在所有領域，特別是人類歷史領域，必須講授出人意料的事情.“在這個昏暗的世界，我們被迫在充滿不確定因素的海洋上航行，時而穿行于確定的群島之間，這就是人類的冒險.今天，我們知道這是未知的冒險，我們需要一種教育，能幫助我們面對這個冒險而不氣餒”.

總之，統計不僅是一種重要的“方法”或“工具”，也是一種思維模式;不僅是一門專業學科，也是一種文化;不僅是一些知識，更是一個人的文化素質.在充斥著各種各樣的信息與噪音的大數據海洋中，對統計學的正確使用可以幫助我們在各種冒險中獲得創新與創業的先機.

【參考文獻】

[1]雷納特·N.凱恩，杰弗里·凱恩.創設聯結：教學與人腦[M].呂梅海，譯.上海：華東師范大學出版社，2004.

[2]趙煥光，章勤瓊，王迪.真理相遇統計[M].北京：科學出版社，2019.

[3]朱辰辰.關于《信號與噪音》的翻譯實踐報告[D].天津：天津師范大學，2014.

[4]茆詩松，周紀薌.概率論與數理統計：第二版[M].北京：高等教育出版社，2000.

[5]達萊爾·哈夫.統計陷阱[M].廖穎林，譯.上海：上海財經大學出版社，2002.