基于非線性模型預測控制的車輛縱向隊列協調控制*

楊秀建，李金雨

（昆明理工大學交通工程學院，昆明 650500）

前言

車輛隊列（vehicular platooning）又稱為車輛編隊，是一列由若干輛汽車組成并按照指定跟馳控制策略安全穩定行駛的車隊。作為智能汽車和智能交通系統實施的一種重要方式，車輛隊列通過車載雷達、車 車（V2V）通信、車 基礎設施（V2I）通信等方式獲取車輛與道路環境信息，實現隊列內車輛的協同運動控制，可以顯著縮短跟馳間距，對緩解交通擁堵、改善交通安全性、降低交通能耗等方面都有積極作用［1-3］。

目前，車輛隊列控制的實施方式正在由巡航控制（adaptive cruise control，ACC）向協同自適應巡航控制（cooperative adaptive cruise control，CACC）的方向發展，CACC是隨著車聯網通信技術的發展在ACC的基礎上進一步結合V2V、V2I等通信方式而產生的一種熱門的車輛隊列實施思路［3-4］。作為車輛隊列實施的關鍵技術，隊列控制一直都是研究的熱點，很多學者都從多智能體系統的角度對隊列的穩定性及控制理論進行了廣泛的研究［5-8］。實際的車輛隊列控制涉及到隊列的整體跟馳控制和隊列中個體車輛的動力學控制兩個方面，目前國內外針對ACC系統的研究多采用分層控制思想，即上層為車輛跟馳控制器，主要考慮車輛的跟馳性能、燃油經濟性和舒適性等因素，通過車載雷達獲取前方車輛的運動信息并決策輸出安全跟馳行駛的期望加速度；下層為車輛動力學控制器，將上層的期望加速度轉化為車輛油門開度或制動力矩，使車輛盡可能實現上層輸出的期望加速度［9-13］。在這種兩層控制結構中，上層的期望跟馳加速度最終都需要通過下層車輛動力學控制來實現，而車輛動力學控制又與車輛自身的動力學特性、載運工況、道路環境等因素有密切關系，車輛動力學的控制性能直接影響隊列的跟馳控制性能，特別是隨著隊列中車輛數量的增加這個問題將更加突出，所以從本質上講，隊列跟馳控制和個體車輛動力學控制需要綜合考慮并協調控制。目前車輛隊列分層控制策略研究的重點還是上層隊列跟馳控制算法，并且一般都是在良好路面條件下對算法進行評價分析。然而，由于這種分層控制結構的上下層控制器獨立設計，上層跟馳控制器在控制決策時沒有考慮個體車輛動力學的實際情況，因而在一些極端操縱工況下，例如在濕滑的低附著路面條件下，由于車輛動力學性能較差而控制困難，可能會出現個體車輛動力學穩定性和隊列跟馳控制目標難以兼顧的情況。這時不但無法實現上層的跟馳控制目標，甚至還會導致追尾碰撞等事故。針對這個問題，一種理想的控制方案是采用集中式控制器對隊列跟馳和車輛動力學穩定性實施一體化控制，但是問題比較復雜；而上下層協調控制的方案，雖然精度不如一體化方案，但是相對比較容易實現。

本文中基于協調控制的思路，提出了一種基于非線性模型預測控制（nonlinear model predictive control，NMPC）的車輛隊列控制方案，在控制決策中綜合考慮車輛跟馳和車輛動力學性能，將安全的跟車間距和各車輪的滑移率作為控制目標，確保車輪滑移率不發生突變且維持在穩定的范圍內。對滑移率進行約束限制，基于序列二次規劃算法（sequential quadratic programming，SQP）計算每一時刻前后軸的期望力矩，從而確保車輛在不同路面附著系數條件下都能安全穩定行駛。

1 非線性單軌車輛模型

為考察實際車輛動力學對隊列跟馳控制的影響，仿真模型采用考慮非線性輪胎力特性的非線性車輛模型。由于僅考慮車輛的縱向運動，所以這里采用3自由度（3DOF）的非線性單軌車輛模型，圖1給出了該模型的結構示意圖。

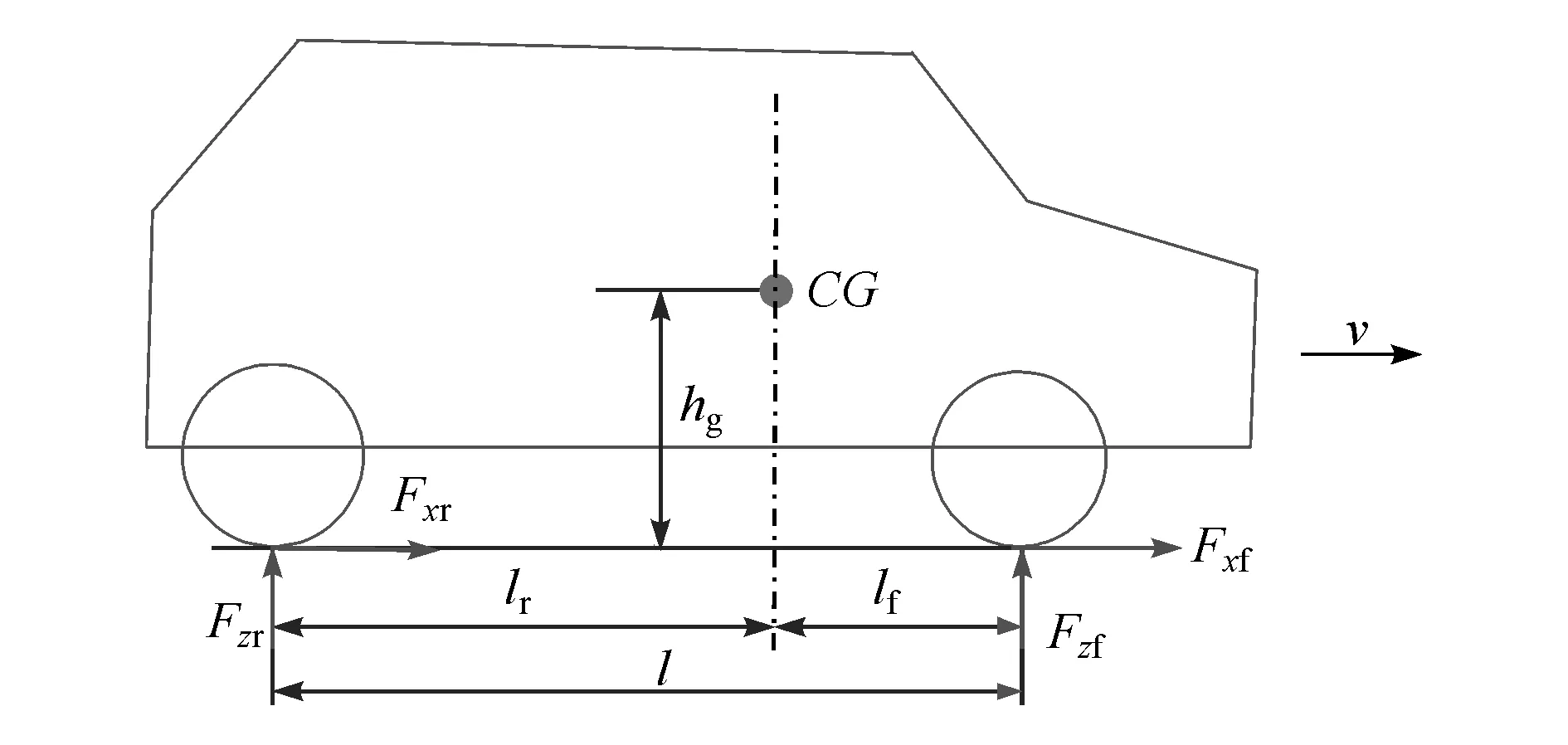
圖1 3DOF非線性單軌車輛模型

3個運動自由度分別為整車的縱向運動、前車輪的旋轉運動和后車輪的旋轉運動，則整車的縱向運動方程可表達為

式中：m為車輛質量；v為車速；Fxf、Fxr分別為前、后輪縱向輪胎力；G為車輛重力；fr為車輪滾動阻力系數。

車輛的非線性動力學特性主要體現在前、后輪縱向輪胎力Fxf和Fxr的非線性特性，因此這里基于純縱滑“魔術公式”非線性輪胎模型［14］來計算Fxf和Fxr，模型具體形式為

式中：μ為路面附著系數；a1～a8為常數；Fz為車輪的法向載荷，具體到前、后輪的法向載荷可分別表達為Fzf、Fzr，如圖1所示；σ為車輪縱向滑移率。

前、后輪的法向載荷Fzf、Fzr可分別計算為

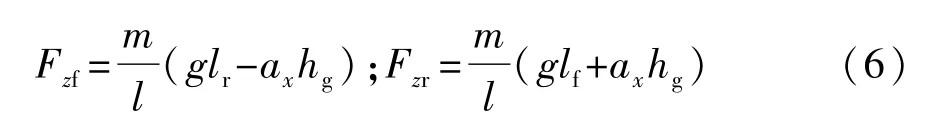
式中：hg為車輛質心高度；ax為車輛縱向加速度。

車輛加速（ax＞0）和制動（ax＜0）時的車輪滑移率可表達為

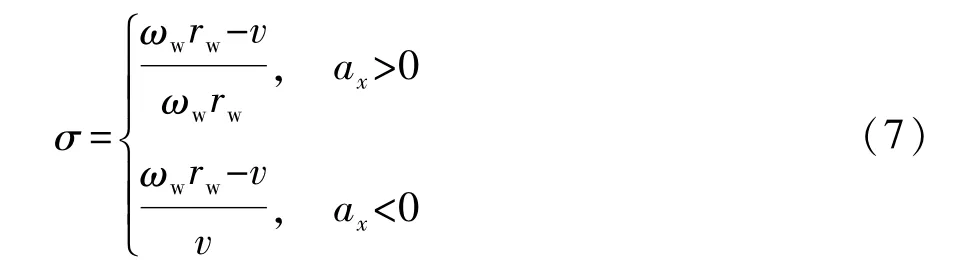
式中：ωw為車輪旋轉角速度；rw為車輪滾動半徑。車輪旋轉角速度ωw通過下面的車輪旋轉動力學方程來計算，即

式中：Iw為車輪轉動慣量；Tw為車輪制動力矩或驅動力矩。

2 基于NMPC的車輛隊列協調控制

2.1 控制方案

典型的車輛隊列如圖2所示，這里不考慮V2V或V2I等通信方式，隊列中的車輛僅通過車載雷達探測與其前方車輛的相對速度、車間距等信息進行跟馳控制，在保持其自身動力學穩定性的基礎上盡可能實現期望的跟馳控制目標。

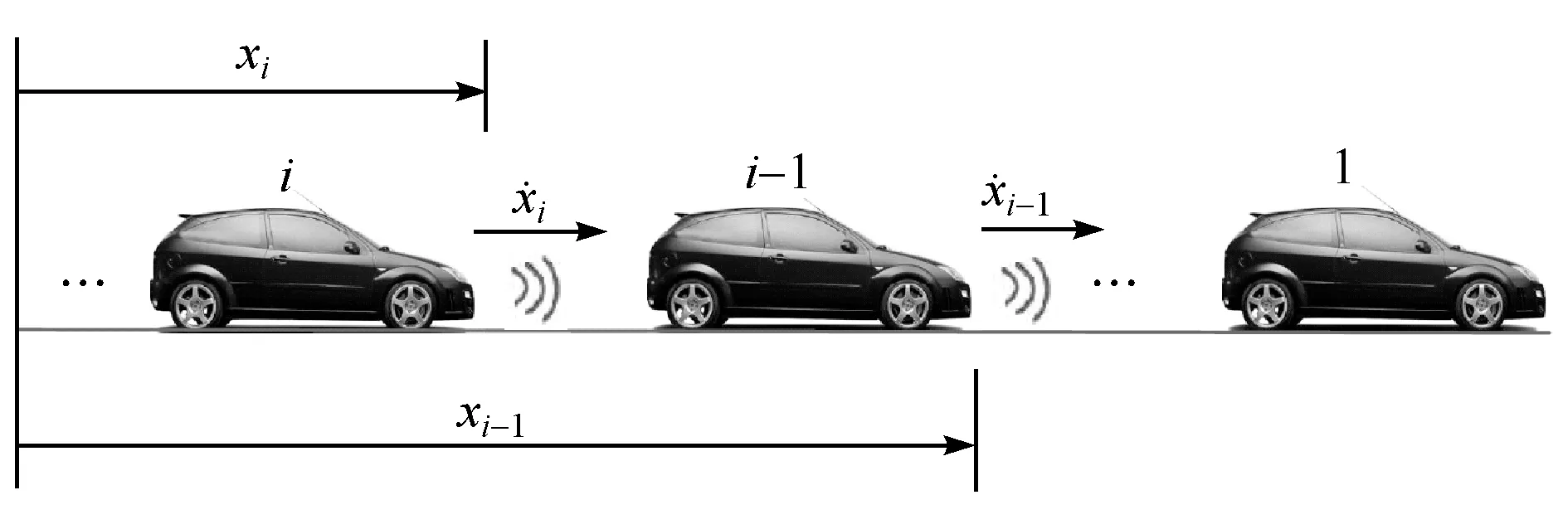
圖2 車輛隊列示意圖

本文中提出的基于NMPC的車輛協調控制整體方案如圖3所示，協調控制主要是綜合權衡隊列的跟馳控制目標與個體車輛的動力學穩定性，基本原則是在保證車輛穩定行駛的基礎上盡可能實現期望的跟馳運動。車輛在低附著路面條件下加速／制動時容易出現由于車輪滑移率突變而失穩的現象，在這種情況下對整個車輛隊列來說將更加難以控制。因此，本方案將反映車輛動力學穩定性的車輪滑移率作為上層隊列控制器控制決策的重要參考。從圖中可以看出，車輛i的NMPC隊列控制器的輸入信息除車速vi、加速度axi以及與前車的車間距Δxi和相對速度Δ·xi外，還有車輛i的前、后車輪的旋轉角速度

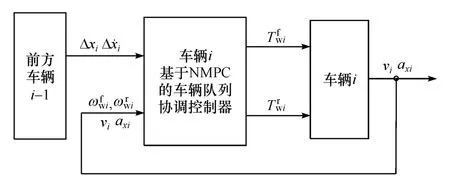
圖3 車輛隊列協調控制方案

車輛隊列控制本質上是非線性車輛動力學與隊列跟馳的協調控制，是一個強非線性、多目標約束優化控制問題。這里采用NMPC控制方法，在滿足滑移率約束使車輛安全穩定行駛的情況下優化求解控制序列，得到車輛i的前、后軸驅動／制動力矩NMPC的預測模型和目標函數中含有非線性動態，與一般的MPC方法類似，也是一個序列有限時域的最優控制問題，大致也分為模型預測、滾動優化和反饋校正3步。首先根據系統狀態空間方程預測系統未來動態，然后在線滾動求解優化問題，最后將解序列的第一個元素施加于系統，通過系統的輸出值修正當前時刻的系統狀態，并結合測得信息進行下一次循環控制［15-16］。

2.2 控制模型

采用車頭時距跟馳策略，車輛i與其前方車輛i-1的期望車間距即安全距離定義為

式中hwi為車頭時距。相應地，車輛i的跟馳誤差為

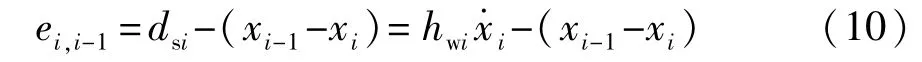
以車輛前軸為例，由式（7）滑移率表達式可得車輛在加速工況下滑移率對時間的導數：

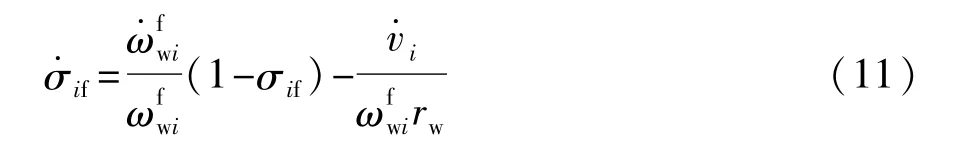
同理，在制動工況下有

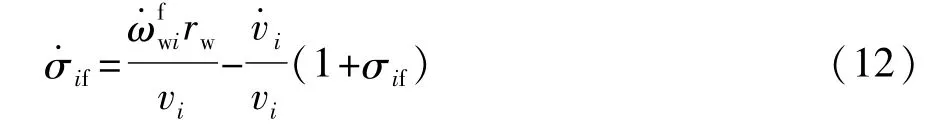
式中：σif為車輛i前軸車輪的滑移率為輪速。結合式（1）和式（8），式（11）加速工況下滑移率的導數公式可改寫為

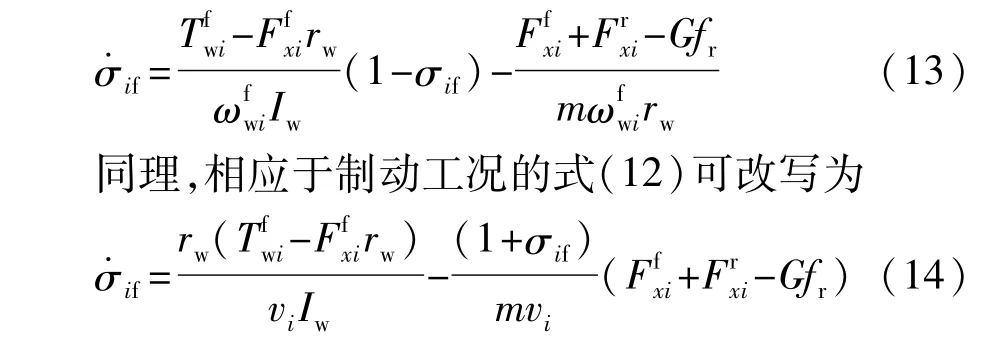
為方便控制器設計，對非線性縱向輪胎力進行線性化處理，車輛i前軸的縱向輪胎力可表達為

式中Kif為車輛i前軸車輪的縱滑剛度，可通過式（16）的擬合表達式計算［17］。

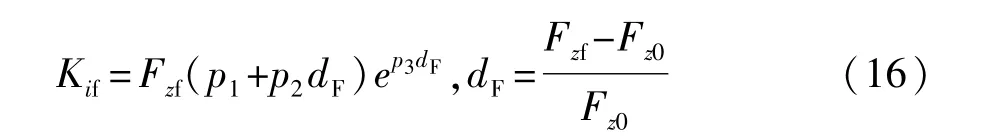
式中：p1、p2、p3為擬合系數；Fz0為常數。

同理，也可以得到車輛后軸車輪的關于滑移率、縱向輪胎力的上述方程。結合式（1）、式（8）、式（13）～式（16）和后軸車輪的相關方程，可得車輛i的控制模型方程，考慮到NMPC控制的需要，這里直接給出其離散形式，即

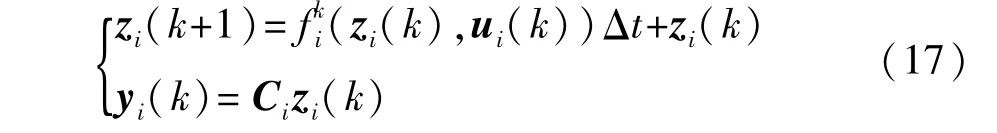
式中：zi＝［vixi］T為系統狀態變量；ui＝［］T為系統輸入；yi＝zi為系統輸出變量；輸出矩陣Ci＝diag（1，1，1，1）為系統狀態量在k時刻的變化梯度；Δt為采樣時間。具體地，各狀態的離散化計算模型分別為

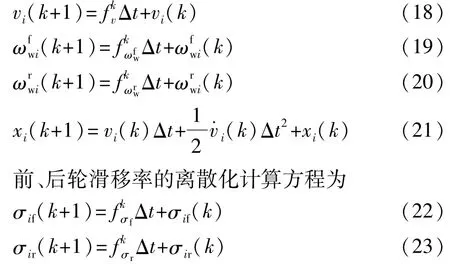
2.3 控制算法設計

以隊列中車輛i為例，基于NMPC車輛隊列協調控制的基本流程思路如圖4所示。在本問題中，目標函數考慮了車輛跟馳控制和車輪滑移率控制兩個方面，約束條件主要是車輪滑移率約束，控制輸入為前、后軸的驅動／制動力矩。

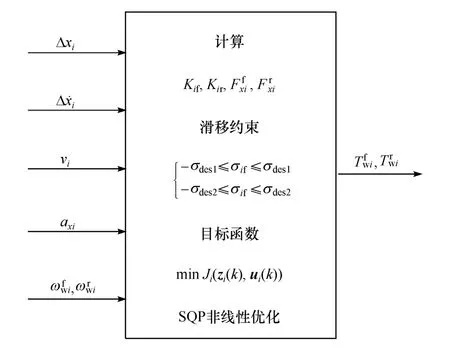
圖4 基于NMPC的車輛隊列協調控制流程

設控制時域和預測時域分別為Nc和Np，在采樣時刻k控制變量序列Ui（k）和系統輸出變量序列Yi（k）分別為

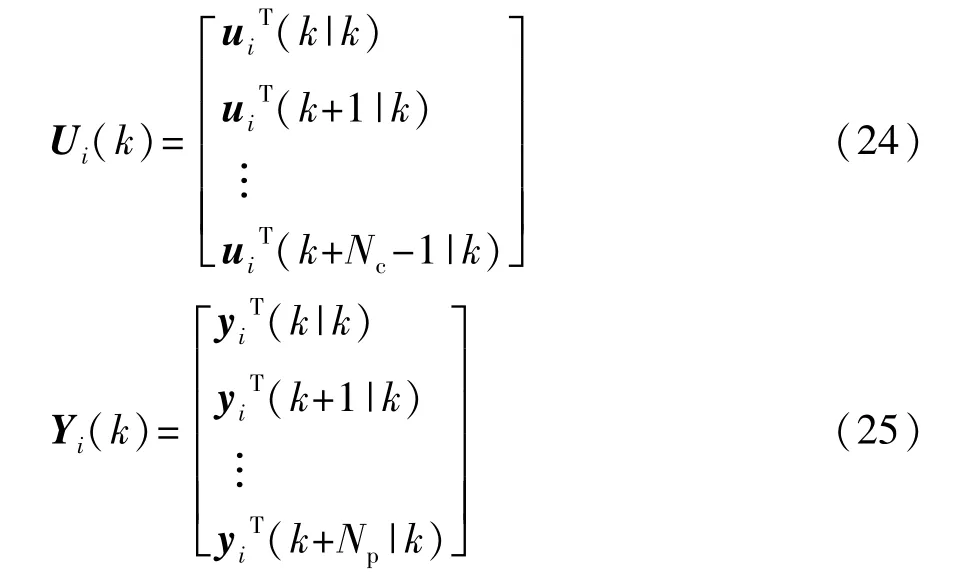
在采樣時刻k，預測控制起始點zi（k）等于zi（k｜k），以此作為系統狀態的初始值來預測系統未來的動態變化。系統狀態和輸出預測分別由式（26）和式（27）給出：

在每一個采樣時刻，利用新測量的車輛狀態信息實時更新系統的狀態預測變量和輸出預測變量，然后進行一次優化求解，將得到最優的驅動／制動力矩作用于隊列中的車輛，在每一個采樣時刻都會進行一次優化求解，直至任務結束。

根據上述對控制系統的描述，為實現隊列中車輛的跟馳控制目標，保證在極限操縱工況下車輪不會發生滑移突變且滑移率保持在穩定的范圍內，建立帶約束的多目標函數，目標函數由3個指標函數Ji1～Ji3組成，具體情況如下。

（1）實現期望的車間距是車輛隊列跟馳控制的主要目標之一，即通過控制使跟馳誤差盡可能小，該控制目標通過指標函數Ji1來實現，即

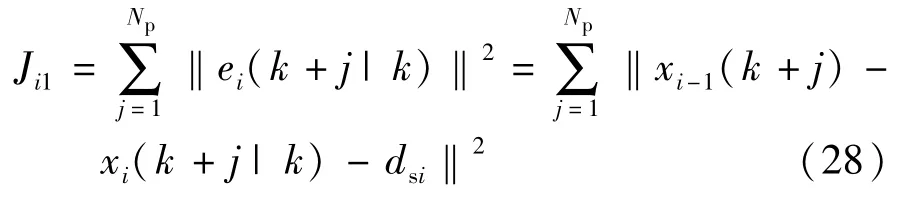
（2）為實現良好的跟馳運動，除了車間距通常還需要將跟馳車速作為一個控制目標，即盡可能與前方車輛速度保持一致，因此定義下述指標函數：

（3）從隊列中個體車輛的動力學穩定性考慮，為防止在極限操縱工況下車輪滑移率出現急劇增加而導致車輛加速／制動失控，期望車輪的圓周速度與車速相差盡可能小，目的是使車輪滑移率保持在較低的水平，這一目標通過指標函數Ji3來體現，即

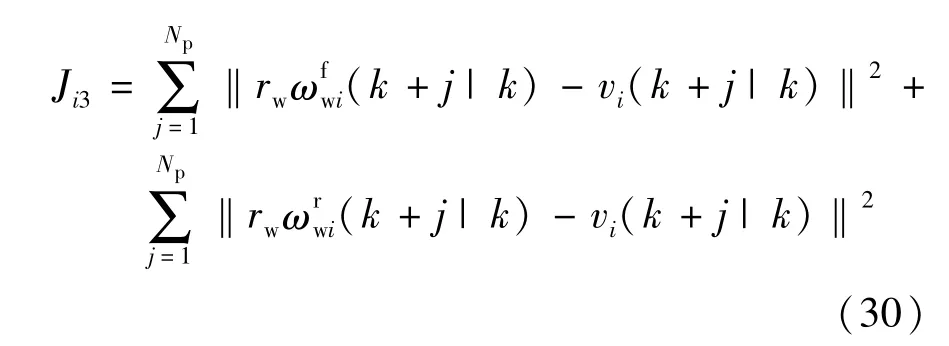
由上述3個指標函數Ji1～Ji3可得NMPC的目標函數為

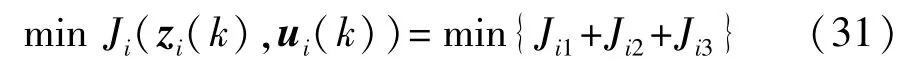
對各性能指標都設置相應的權重，通過調整權重來調整各性能的控制要求，從而可以綜合提高車輛隊列的跟馳性能和個體車輛的動力學穩定性。

為防止車輪滑移率突變，NMPC需在限定的車輪滑移率范圍內進行每一次優化求解，因此定義前、后軸車輪滑移率約束：

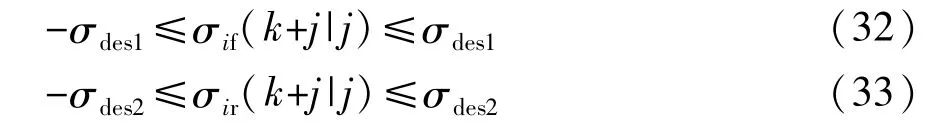
2.4 NMPC優化求解

根據非線性控制模型方程和上述各目標函數方程的定義，優化問題可表示為

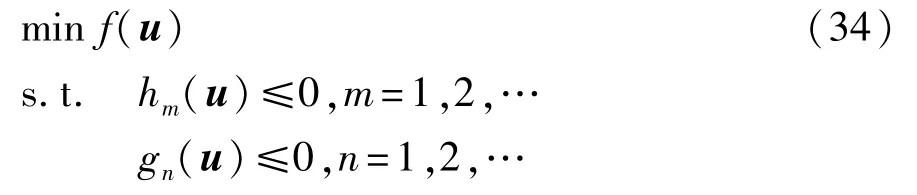
式中：hm（u）為線性不等式約束；gn（u）為非線性不等式約束。

序列二次規劃（SQP）是求解一般非線性約束規劃問題的一種非常有效的方法，它在每個迭代點處求解構造的一個二次規劃子問題作為迭代的搜索方向，然后進行一維搜索得到新的迭代點，直到迭代點列靠近非線性規劃問題的最優解［18］。SQP算法流程如下：

（1）取合理的初始解u0；

（2）求解二次規劃子問題

得到搜索方向dk；

（3）如果｜dk｜＜ε或者k＞Nc，則停止，反之繼續進行下一步；

（4）找到步長αk，滿足0≤αk≤1且

f（uk＋αkdk）＜f（uk）

（5）令uk＋1＝uk＋αkdk，k＝k＋1，轉到步驟（2）。

3 仿真分析

通過模型仿真對所提出的協調控制方案進行評價分析，以圖2所示的同質車輛隊列為對象，這里僅考慮3輛車的情況，領頭車輛序號為1，后面的跟馳車輛序號依次為2和3。隊列中各車輛均采用前文所建立的非線性單軌車輛模型，所以該車輛隊列模型能夠反映在低附著等極限操縱工況下的隊列跟馳控制性能。

所采用的車輛模型參數為：m＝1700 kg，lf＝1.1 m，lr＝1.6 m，hg＝0.65 m，rw＝0.25 m，fr＝0.01，Iw＝1 kg·m2，g＝9.81 m／s2。考慮隊列制動與隊列加速兩種操縱工況，分別考察在μ＝0.8和μ＝0.3高、低路面附著條件下的隊列跟馳控制響應。首先考察隊列制動控制，初始時隊列以24 m／s的速度勻速行駛，某時刻領頭車輛從24的速度勻減速到18 m／s，然后勻速行駛，后面的跟馳車輛采用定時距跟馳策略，則在高、低路面附著條件下基于NMPC的隊列跟馳控制響應分別如圖5和圖6所示。圖中給出了車速、跟馳誤差和車輪的滑移率響應，其中車速和跟馳誤差反映的是隊列的跟馳性能，而車輪滑移率反映的是個體車輛動力學性能。圖中：e2，1為車輛2跟馳車輛1（領頭車）的誤差；e3，2為車輛3跟馳車輛2的誤差；σ2f、σ2r分別為車輛2前、后軸車輪的滑移率，σ3f、σ3r分別為車輛3前、后軸車輪的滑移率。可以看出，所提出的基于NMPC的控制方案可以實現隊列的跟馳控制，即使是在μ＝0.3的低附著路面條件下，也可以實現良好的跟馳控制效果，并且車輛動力學性能穩定。

在加速工況下，初始時隊列以15 m／s的速度勻速行駛，某時刻領頭車輛勻加速到24 m／s，然后勻速行駛，圖7和圖8分別給出了高、低兩種路面附著條件下隊列加速跟馳控制的響應。可以看出，與高附著路面情況相比，在低附著條件下車速、跟馳誤差等跟馳狀態波動較大，調整時間較長，盡管如此，仍可實現隊列的跟馳控制，各車輪滑移率也都控制在較小的范圍內，能夠保證車輛安全穩定行駛。低附著路面條件下跟馳狀態波動較大主要是由于NMPC控制器在控制決策中考慮了個體車輛動力學（車輪滑移率），在隊列跟馳和保持個體車輛動力學穩定性兩者間進行了折中處理，決策輸出的期望跟馳加速度從車輛跟馳控制的角度來看并不是最優的，但是對保持個體車輛的動力學穩定性是有利的，即通過損失部分跟馳性能來提高車輛的行駛穩定性。

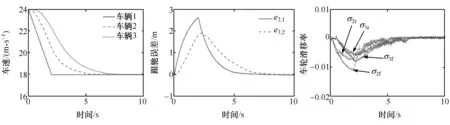
圖5 高附著路面條件下車輛隊列制動跟馳響應（μ＝0.8）

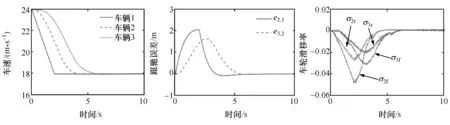
圖6 低附著路面條件下車輛隊列制動跟馳響應（μ＝0.3）

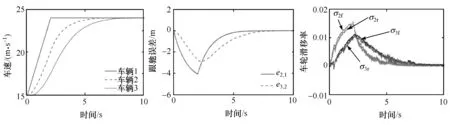
圖7 路面附著系數為0.8時車輛隊列加速響應情況

圖8 路面附著系數為0.3時車輛隊列加速響應情況

4 結論

車輛隊列采用上、下兩層的分層控制結構時，結構清晰易于實現，但是這種方案也存在上下層控制器間聯系不夠密切的問題，即在低附著系數等極限行駛工況下，下層控制器可能無法實現上層的期望跟馳要求，甚至導致隊列車輛追尾碰撞事故的發生。

針對這一問題，本文中提出了隊列跟馳和車輛動力學協調控制的思路，基本思想是在保證隊列中個體車輛安全穩定行駛的基礎上，盡可能實現隊列跟馳控制的目標。基于NMPC方法設計了車輛隊列協調控制策略，設計了包括跟馳間距誤差、跟馳速度誤差以及車速與輪速差3個子目標的優化目標函數，將隊列跟馳與車輛動力學穩定性的協調控制轉化為約束優化控制問題。基于非線性車輛模型的3車輛同質隊列對所提出的控制方案進行了仿真分析，考察了高、低兩種路面附著條件下的加速和制動跟馳工況。結果表明，所提出的基于NMPC的隊列跟馳協調控制策略可在大范圍操縱工況下實現隊列的跟馳控制，并且都可以保證車輛安全穩定行駛，這是由于所提出的協調控制方案，可在隊列跟馳和保持個體車輛動力學穩定性兩者間合理進行折中處理，決策輸出合理的跟馳期望加速度。