中外規(guī)范關(guān)于圓柱殼環(huán)向穩(wěn)定承載力比較

俞棟華 吳金池

(湖北省工業(yè)建筑集團(tuán)有限公司，湖北武漢 430064)

由于各個(gè)國(guó)家國(guó)情不同，鋼結(jié)構(gòu)設(shè)計(jì)分析和計(jì)算所依據(jù)的標(biāo)準(zhǔn)也有所區(qū)別。在鋼結(jié)構(gòu)工程中，圓柱殼已被廣泛應(yīng)用于海洋平臺(tái)、塔桅結(jié)構(gòu)、倉(cāng)儲(chǔ)、容器、煙風(fēng)管道等。圓柱殼在風(fēng)荷載或負(fù)壓作用下容易發(fā)生局部失穩(wěn)。目前，中國(guó)規(guī)范SY/T 10030—2004［1］中有圓管構(gòu)件穩(wěn)定計(jì)算的規(guī)定，德國(guó)規(guī)范 DIN 18800 Part 4［2］和歐洲規(guī)范 EN 1993－1-6:2007［3］中均有殼體穩(wěn)定計(jì)算的規(guī)定。針對(duì)圓柱殼失穩(wěn)這類工程情況，選取不同半徑、厚度、長(zhǎng)度、邊界條件的圓柱殼，分別按照中國(guó)、德國(guó)、歐洲規(guī)范中的相關(guān)規(guī)定計(jì)算穩(wěn)定承載力，分析總結(jié)它們之間的差異。

1 圓柱殼環(huán)向穩(wěn)定承載力計(jì)算方法

關(guān)于圓柱殼環(huán)向穩(wěn)定承載力計(jì)算，文獻(xiàn)［1］引入臨界環(huán)向屈曲系數(shù)Ch，該系數(shù)考慮了API Spec 2B［4］公差范圍之內(nèi)的初始幾何缺陷的影響，未考慮邊界條件的影響。文獻(xiàn)［2］［3］都是在屈服強(qiáng)度基礎(chǔ)上考慮一個(gè)折減系數(shù)，折減系數(shù)考慮了邊界條件的影響，且文獻(xiàn)［3］引入了與制造質(zhì)量相關(guān)的彈性缺陷折減系數(shù)。各國(guó)關(guān)于圓柱殼環(huán)向穩(wěn)定承載力的具體計(jì)算方法如下所述。

1.1 中國(guó)規(guī)范環(huán)向穩(wěn)定承載力計(jì)算方法

根據(jù)文獻(xiàn)［1］式 3.2.5-6，圓柱殼臨界環(huán)向屈曲應(yīng)力計(jì)算公式如下:

當(dāng) Fhe≤0.55Fy時(shí):

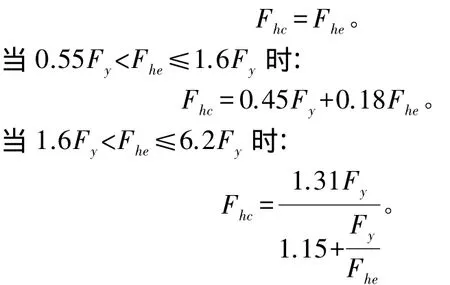
當(dāng) Fhe＞6.2Fy時(shí):

其中，F(xiàn)he為彈性環(huán)向屈曲應(yīng)力，根據(jù)文獻(xiàn)［1］式3.2.5-4計(jì)算如下:

其中，F(xiàn)y為鋼材的屈服強(qiáng)度;E為鋼材的彈性模量;D為圓柱殼外徑;t為圓柱殼壁厚;Ch為臨界環(huán)向屈曲系數(shù)，根據(jù)文獻(xiàn)［1］式 3.2.5-5 計(jì)算如下:

其中，M 為幾何參數(shù)，根據(jù)文獻(xiàn)［1］式 3.2.5-5計(jì)算如下:

1.2 德國(guó)規(guī)范環(huán)向穩(wěn)定承載力計(jì)算方法

根據(jù)文獻(xiàn)［2］式44，圓柱殼環(huán)向屈曲應(yīng)力計(jì)算公式如下:

其中，fyk為鋼材的屈服強(qiáng)度;χ1為屈曲折減系數(shù)，根據(jù)文獻(xiàn)［2］式7計(jì)算如下:

當(dāng) λsφ≤0.4 時(shí):

其中，λsφ為通用纖薄度，根據(jù)文獻(xiàn)［2］式2計(jì)算如下:

其中，σφSi為理想彈性臨界應(yīng)力，根據(jù)文獻(xiàn)［2］式 33～36計(jì)算如下:

其中，E為鋼材的彈性模量;r為圓柱殼半徑;t為圓柱殼壁厚;Cφ為和邊界條件有關(guān)系數(shù)，兩端鉸支時(shí)取1，一端鉸支一端嵌固時(shí)取1.25，兩端嵌固時(shí)取1.5。

1.3 歐洲規(guī)范環(huán)向穩(wěn)定承載力計(jì)算方法

根據(jù)文獻(xiàn)［3］式8.12，圓柱殼環(huán)向屈曲應(yīng)力計(jì)算公式如下:

其中，fyk為鋼材的屈服強(qiáng)度;χθ為屈曲折減系數(shù)，根據(jù)文獻(xiàn)［3］式 8.13～8.15 計(jì)算如下:

其中，λθ0為極限長(zhǎng)細(xì)比，取 0.4;β為塑性區(qū)系數(shù)，取0.6;η 為交互指數(shù)，取 1.0;αθ為彈性缺陷折減系數(shù)，與制造質(zhì)量有關(guān)，極好時(shí)取 0.75，高時(shí)取 0.65，一般時(shí)取 0.5;λθp為塑性極限相對(duì)長(zhǎng)細(xì)比，根據(jù)文獻(xiàn)［3］式8.16計(jì)算如下:

其中，λθ為相對(duì)長(zhǎng)細(xì)比系數(shù)，根據(jù)文獻(xiàn)［3］式8.17計(jì)算如下:

其中，σθRcr為彈性臨界應(yīng)力，根據(jù)文獻(xiàn)［3］式 D.20～D.25計(jì)算如下:

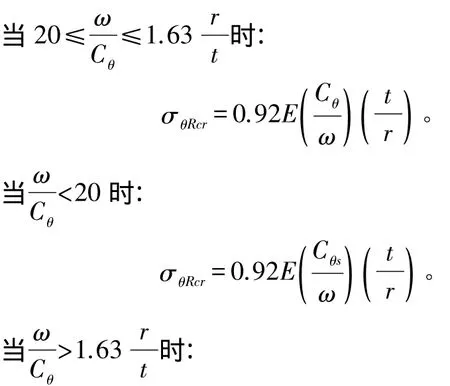
其中，E為鋼材的彈性模量;Cθ為系數(shù)，兩端鉸支時(shí)取1，一端鉸支一端嵌固時(shí)取 1.25，兩端嵌固時(shí)取 1.5;Cθs為系數(shù)，按以下要求取值:

其中，ω為無(wú)量綱長(zhǎng)度系數(shù)，根據(jù)文獻(xiàn)［3］式D.19計(jì)算如下:

其中，l為圓柱殼長(zhǎng)度。

2 圓柱殼環(huán)向穩(wěn)定承載力算例

2.1 不同半徑穩(wěn)定承載力對(duì)比

選取厚度為12 mm，長(zhǎng)度為7.5 m，邊界條件為一端鉸支一端嵌固，半徑分別為 0.5 m，0.75 m，1 m，1.25 m，1.5 m，1.75 m的圓柱殼，根據(jù)文獻(xiàn)［1］～［3］計(jì)算方法，分別計(jì)算各自環(huán)向穩(wěn)定承載力，制成不同半徑圓柱殼穩(wěn)定承載力統(tǒng)計(jì)表，見(jiàn)表1。

表1 不同半徑圓柱殼穩(wěn)定承載力 MPa

根據(jù)表1數(shù)據(jù)，制成不同半徑圓柱殼穩(wěn)定承載力折線圖，見(jiàn)圖1。

圖1 不同半徑穩(wěn)定承載力折線圖

由圖1可知，中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力基本相等，且均與半徑成反比。

2.2 不同厚度穩(wěn)定承載力對(duì)比

選取半徑為1 m，長(zhǎng)度為7.5 m，邊界條件為一端鉸支一端嵌固，厚度分別為 8 mm，10 mm，12 mm，14 mm，16 mm，18 mm的圓柱殼，根據(jù)文獻(xiàn)［1］～［3］計(jì)算方法，分別計(jì)算各自環(huán)向穩(wěn)定承載力，制成不同厚度圓柱殼穩(wěn)定承載力統(tǒng)計(jì)表，見(jiàn)表2。

表2 不同厚度圓柱殼穩(wěn)定承載力 MPa

根據(jù)表2數(shù)據(jù)，制成不同厚度圓柱殼穩(wěn)定承載力折線圖，見(jiàn)圖2。

圖2 不同厚度穩(wěn)定承載力折線圖

由圖2可知，中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力基本相等，且均與厚度成正比。

2.3 不同長(zhǎng)度穩(wěn)定承載力對(duì)比

選取半徑為1 m，厚度為12 mm，邊界條件為一端鉸支一端嵌固，長(zhǎng)度分別為 2.5 m，5 m，7.5 m，10 m，12.5 m，15 m的圓柱殼，根據(jù)文獻(xiàn)［1］～［3］計(jì)算方法，分別計(jì)算各自環(huán)向穩(wěn)定承載力，制成不同長(zhǎng)度圓柱殼穩(wěn)定承載力統(tǒng)計(jì)表，見(jiàn)表3。

表3 不同長(zhǎng)度圓柱殼穩(wěn)定承載力 MPa

圖3 不同長(zhǎng)度穩(wěn)定承載力折線圖

根據(jù)表3數(shù)據(jù)，制成不同長(zhǎng)度圓柱殼穩(wěn)定承載力折線圖，見(jiàn)圖3。由圖3可知，中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力基本相等，且均與厚度成反比。

2.4 不同邊界條件穩(wěn)定承載力對(duì)比

表4 不同邊界條件圓柱殼穩(wěn)定承載力 MPa

選取半徑為1 m，厚度為12 mm，長(zhǎng)度為7.5 m，邊界條件分別為兩端鉸支、一端鉸支一端嵌固、兩端嵌固的圓柱殼，根據(jù)文獻(xiàn)［1］～［3］計(jì)算方法，分別計(jì)算各自環(huán)向穩(wěn)定承載力，制成不同邊界條件圓柱殼穩(wěn)定承載力統(tǒng)計(jì)表，見(jiàn)表4。

根據(jù)表4數(shù)據(jù)，制成不同邊界條件圓柱殼穩(wěn)定承載力折線圖，見(jiàn)圖4。

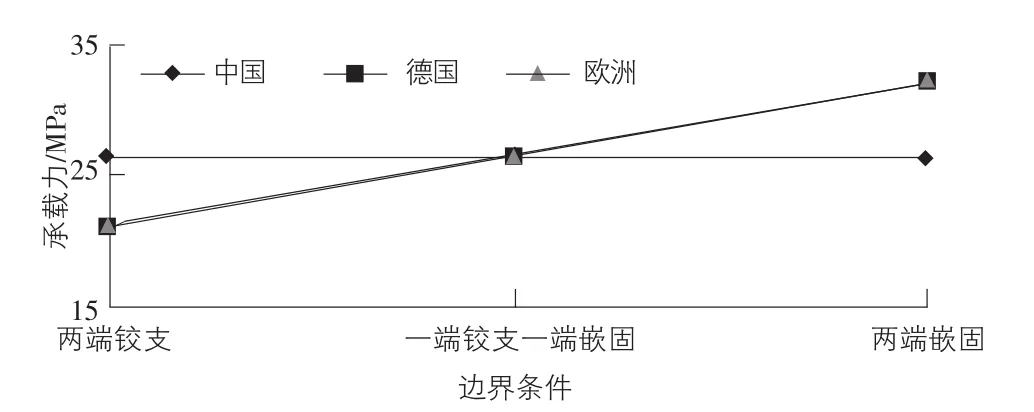
圖4 不同邊界條件穩(wěn)定承載力折線圖

由圖4可知，中國(guó)規(guī)范計(jì)算的穩(wěn)定承載力與邊界條件無(wú)關(guān)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力兩端嵌固時(shí)最大、一端鉸支一端嵌固時(shí)次之、兩端鉸支時(shí)最小。當(dāng)半徑、厚度、長(zhǎng)度已定，兩端鉸支時(shí)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力相等且小于中國(guó)規(guī)范計(jì)算值;一端鉸支一端嵌固時(shí)，中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力基本相等;兩端嵌固時(shí)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力相等且大于中國(guó)規(guī)范計(jì)算值。

3 結(jié)語(yǔ)

1)中國(guó)規(guī)范計(jì)算的穩(wěn)定承載力未考慮與邊界條件的關(guān)系，計(jì)算結(jié)果與實(shí)際值存在差異。2)德國(guó)規(guī)范計(jì)算的穩(wěn)定承載力與歐洲規(guī)范中彈性缺陷折減系數(shù)取0.65時(shí)計(jì)算值相等。當(dāng)邊界條件為一端鉸支一端嵌固時(shí)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力與中國(guó)規(guī)范基本相等。3)中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力均與半徑成反比、與厚度成正比、與長(zhǎng)度成反比。4)當(dāng)半徑、厚度、長(zhǎng)度已定，中國(guó)規(guī)范計(jì)算的穩(wěn)定承載力與邊界條件無(wú)關(guān)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力兩端嵌固時(shí)最大、一端鉸支一端嵌固時(shí)次之、兩端鉸支時(shí)最小。兩端鉸支時(shí)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力相等且小于中國(guó)規(guī)范計(jì)算值;一端鉸支一端嵌固時(shí)，中國(guó)、德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力基本相等;兩端嵌固時(shí)，德國(guó)、歐洲規(guī)范計(jì)算的穩(wěn)定承載力相等且大于中國(guó)規(guī)范計(jì)算值。