大跨徑連續梁橋中的溫度應力研究

蔡 潔，周清忘，陳 偉

（1.湖北工業大學，湖北武漢 430068；2.武漢建工集團股份有限公司，湖北武漢 430068）

0 引言

在我國，橋梁是連接交通的重要設施，從新中國成立之初到現在，橋梁的發展飛速提升。與此同時，橋梁的建設要求也越來越高。在溫度荷載的作用下，由于構件中混凝土材料的特性連續梁橋會產生裂縫。裂縫的原因是內部產生較大的應力和應變。裂縫在這種情況下形成后，混凝土中的鋼筋會與空氣中的成分發生相應的化學反應，這樣會加劇混凝土碳化，從而導致鋼筋嚴重銹蝕。由鋼筋銹蝕而產生的裂縫會不斷地擴大，從而導致橋梁在高應力情況下瞬間損壞，在理論上這種情況被稱為橋梁發生的脆斷破壞，對來往車輛的安全和橋梁的使用有著重要的影響。橋梁在承重的過程中，除了受到行車荷載及橋梁本身自重的作用外，溫度荷載的作用也是不可避免的，氣候因素及材料因素是溫度荷載的重要因素。

1 溫度荷載的特點

在探究和分析溫度應力時，溫度荷載是分析的前提和關鍵。橋梁在承受的荷載中，溫度荷載和別的荷載是不同的，且具有本質性的區別，主要在于溫度荷載具有空間性、結構性、時間性［1］。混凝土橋梁構件的表面溫度和內部溫度在不斷變化。自然環境條件變化引起的溫度負荷一般可分為3種類型:年度溫度變化負荷、突然降溫負荷和日照溫度負荷。各種溫度變化的特點如表1所示。

溫度分布。在混凝土結構中，描述結構中各點和表面在某一時刻的溫度狀態稱為溫度分布。由于混凝土材料本身的特點，它的導熱系數小，產生溫度變化的時候其內部溫度的變化滯后于外部溫度的變化，正是由于這種溫度變化情況下熱量差的存在，形成了溫度非線性不規律分布的狀態［1］。由于混凝土本身的特點，在溫度的作用下，其內部溫度的分布比較明顯。

2 溫度應力及產生原因

2.1 溫度應力

隨著在前人學者的基礎上進行多次試驗以及理論研究的深入，人們逐漸開始認識到溫度分布的非線性不規律分布的變化問題。在20世紀60年代初，英國學者Stephenson［1］進行了一系列關于溫度荷載方面的研究，從他的研究成果中，人們認識到，對于溫度應力的研究不僅要考慮氣溫作用的影響，還要考慮日照作用的影響。這一成果讓研究人員在考慮溫度應力時既要考慮氣溫作用的影響，也要考慮日照作用的影響。

溫度應力在分布上具有明顯的時間性、非線性、不規律性。溫度應力分為兩種:一種是由于結構構件中纖維之間的溫度差引起纖維之間相互約束產生的應力，稱為溫度自約束應力或溫度自應力［2］；另一種是由于結構或系統內部構件，因其構件溫度不同，產生不同的變形。構件在溫度作用下產生不同的變形，且受到整體結構外支撐的約束會產生相應的次應力（構件變形），或稱其為溫度次約束應力。

表1 各種溫度荷載特點

2.2 產生的原因

環境變化引起橋梁結構的溫度效應可分為二類，局部溫差效應和年溫差效應。年度溫差效應對橋梁結構的主要影響將導致均勻的溫度下降或均勻的溫度上升，橋梁各部分的縮短或者對應的伸長。當上述結構的位移或者構件的變形在相應地受到限制時，這樣的情況也會導致構件結構產生溫度二次約束應力（構件變形）［3］。產生這種情況的主要原因是溫度突然下降或太陽輻射，并且傳熱（熱傳導）方法在結構的每個部分上分布都是不均勻的，表現出非線性特點。

對于靜定結構，橋梁截面上將產生相應的自應力。超靜定結構除了產生截面自應力，還將引起結構變形。在溫度的作用下，日照溫差不同對橋梁結構的影響也有相應的變化。在受到日照輻射強度大小、日照時間長短、橋梁地理方位、地形地貌、地理位置等隨機因素的影響下，這些因素會使橋梁結構表面和內部溫差分布呈現瞬時的不均勻分布規律，人們把這種情況稱為溫度場［3-4］。溫度梯度是溫度變化的表現，溫度梯度的變化有線性變化和非線性變化之分。

線性變化：由于溫度差異的作用，梁式結構將發生相應的撓曲變形，變形之后服從材料力學中的平截面假定。因此，在靜定梁式結構中，溫度梯度的線性規律性變化在力學性能中只會引起橋梁結構的位移而不會在此基礎上產生相應的溫度內力（區別于超靜定結構）。但對于多約束限制超靜定結構的情況下，這種超靜定結構在力學性能上不僅會引起橋梁結構的位移，也會在橋梁位移變化的基礎上產生相應的溫度應力（多約束下的超靜定結構）。

非線性變化：橋梁（靜定結構）在發生撓曲變形時應該服從材料力學中的平截面假定，自相平衡的約束應力為溫度自應力δt(y)。然而在多余約束下除了自應力外，還有結構的變形。這種力學性能被稱為超靜定結構，除了溫度本身產生的自應力δt(y)外。人們還應該考慮除本身應力外，多余的約束阻止結構發生相應的撓曲。產生的溫度次內力引起溫度次應力δtx(y)。在綜合考慮的情況下，產生相應的總溫度應力為：δτ(y)= δtx(y)+δt(y)。

3 溫度荷載的求解理論

在眾多相對應的橋梁結構中，由于橋梁內部的結構特點和在自然條件下產生相應的溫度變化和溫度分布是每一刻都在發生變化的。在日溫和年溫的綜合影響作用下，溫度荷載隨時間和各種因素的變化是一個比較復雜的函數，要精確地求解函數從實際上來說是非常困難的。分析瞬時溫度也非常困難，在考慮問題的時候，忽略次要問題抓住主要問題，研究對橋梁影響的最不利溫度梯度，減小其對橋梁使用過程中的影響［4］。對于溫度荷載求解過程，人們在實際情況和理論上通常采用一種便于表現的方式；比如用Fourier的熱傳導微分方程或者半理論半經驗公式來進行相應的求解。

Fourier的熱傳導微分方程表示：混凝土構件由于本身材料性質的特點，在發生熱傳遞交換的過程中產生的主要原因是內外溫度的不均勻變化導致混凝土構件發生熱傳遞。因此人們在研究熱傳遞時，應從各方面去了解相應的溫度分布情況。橋梁結構的內外溫度與時間和空間有關，并且是與時間、空間構成相應有關的函數形式。可以以相應的函數形式來體現其中的變化規律，因此結構內部或外部任意一點的瞬間溫度Ti可以表示為如下的函數形式，函數表示為（1）所示。

從式子中可以看出任意時間點的溫度Ti不僅與三維坐標相關，而且還與時間t有關，為了便于明確表現它們之間的關系，以平截面假定力學性能；各向同性，各向均勻，把混凝土看成是各向均勻的且各向同性的固體。根據Fourier的熱傳導理論知識和相應的彈性力學知識，推出如下的三維非穩定狀態熱傳導方程，方程如（2）所示。

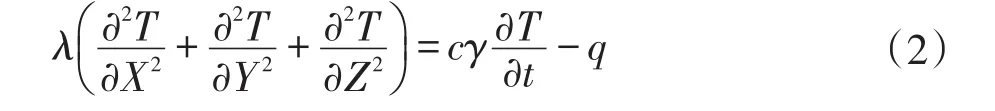
式中：c—混凝土比熱；

γ—混凝土容重；

q—混凝土單位體積放出熱量（當不考慮混凝土水化熱時q=0）；

λ—混凝土導熱系數。

由于溫度場的復雜和多變，比較好的方法是采用一維的傳導公式，簡化計算。式（2）可以簡化為；

在求解熱傳導微分方程時，應該考慮瞬態的導熱問題（其本質上是在定解條件下對導熱微分方程求解）。定解條件應具有相應的初始條件和邊界條件，以下為初始條件和邊界條件的兩種情況。

（1）初始條件：初始條件下整體溫度變化較為均勻，此時t=0，溫度分布為如下函數形式。

（2）邊界條件1；混凝土表面溫度T是已知函數，即：

T（t）=f（t）（表面溫度等于水溫）

邊界條件2；混凝土在與空氣接觸時，表面溫度T和氣溫T0及日輻射的關系可以表示為如下函數形式。

β—總熱交換系數；

S—日輻射強度；

αS—結構物表面日輻射熱量吸收系數；

N—計算板面的外法線方向。

結構物中內表面，邊界條件為如下函數表示：

結構物中外表面，邊界條件為如下函數表示：

式中：

Tc—蔭蔽中溫度；

Tb—結構物內部空間氣溫；

βs—對流熱交換系數；

βα—內部綜合放熱系數。

在以上二類邊界的條件中，人們認為最后一種普遍與實際情況下的周邊條件狀態最為接近。但是得到可靠的數據關鍵點在于放熱系數，放熱系數在規范中并沒有其明確的規定，在實際工程中人們常采用實測溫度作為其邊界條件。

由于熱傳導微分方程在計算過程中確定參數比較困難，工程中常常采用數理統計的方法，考慮對溫度影響大的主要因素，忽略次要因素，根據實際經驗，建立半經驗半理論的公式。橋梁結構的主要熱源來自太陽輻射，輻射增強，橋梁表面溫度升高，相應的輻射減小，溫度隨之降低。環境溫度基本決定了初始溫度條件，風速對結構的表面溫度起關鍵作用，當輻射增強，風速為0時，結構最外層溫度升到最高，由于此時風速影響較小，可不考慮。但是在降溫時，不能忽略風速的影響。

劉興法［5］對實時監測所得到的數據進行分析，認為溫度梯度形式可如下表示。

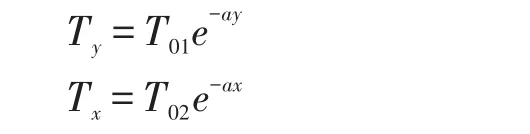
式中：T01—表示沿梁高方向的溫差；

T02—表示沿梁寬方向的溫差；

a—與結構形式、部位方向和時刻有關的因素。

求溫度應力的方法，熱傳導方程的思維過程復雜，但是能真實地描述混凝土結構在實際狀態下的熱交換規律；半經驗法需要大量豐富的實際監測數據為基礎，但過程比較容易掌控，相比前者更好。

4 結語

本文分析了大跨度混凝土橋梁中溫度荷載的特點、溫度分布、溫度應力以及產生原因、求解理論等，相信對以后橋梁的實際施工具有一定的參考和實用價值。