一種緯度估計算法優化及誤差抑制技術研究

劉 洋，莫明崗，張吉先，郭玉勝，鄧繼權

(北京自動化控制設備研究所，北京 100074)

0 引言

通常情況下，慣導系統初始對準需要外部輸入具有一定精度的當地地理緯度。然而對于航海用慣導系統，艦船在戰時會遇到衛星信號受干擾等情況導致無法獲取準確的當地地理位置信息，這就要求慣導系統具備艦船航行中自尋緯度的能力[1-3]。文獻[2]提出了一種晃動基座緯度估計方法，通過慣性系下不同時刻重力加速度向量的夾角求取緯度，但該方法無法適用于動基座情況。文獻[3]在該方法的基礎上，提出了一種航行中緯度估計方法，通過引入計程儀輔助速度信息，補償由于載體機動所產生的誤差[4]。為降低慣性器件測量噪聲的影響[5]，在計算過程中對測量的重力加速度進行積分以提高緯度估計精度[6]，但該方法對重力加速度積分時，積分區間的選擇沒有充分利用所有的測量信息[7]，使緯度估計精度受到一定影響。

本文提出了一種慣導系統行進中緯度估計算法優化及誤差抑制方法，首先分析了緯度估計的主要誤差來源。在此基礎上，對重力加速度積分區間的選取進行推導并給出了最優積分區間的選取方式，充分利用了整個緯度估計時間內的所有采樣信息，提高了緯度估計精度。另外針對艦船在航行中受到的外部擾動，采用最小二乘擬合的方式，對陀螺和加速度計的測量誤差進行抑制，提高了艦船行進中慣導系統的緯度估計精度。

1 緯度估計方法

圖1 海上航行中自尋緯度示意圖Fig.1 Self-seeking of latitude in sea navigation

設對準初始時刻t1系統位于A點，經過一段時間，t2時刻系統位于B點。可以得到

|Ao′|=|Bo′|=|Ao|cosL

(1)

從而有

(2)

又因為

(3)

根據式(1)～式(3)可以得到

(4)

(5)

其中

(6)

(7)

可以得到

(8)

角度α根據時間t1與t2得到

α=ωie×(t2-t1)

(9)

式中，ωie為地球自轉角速率。

2 緯度估計最優積分區間選取

2.1 角度θ的最優區間分析

圖2 積分區間示意圖
Fig.2 Integral interval diagram

(10)

根據式(10)可將用于計算角度θ的速度增量記為

(11)

(12)

(13)

(14)

由式(14)可以分析出，為了使采樣后方差變小，應通過增大分母的方式，這就需要擴大Δvib0的積分范圍，將式(11)改為

(15)

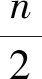
(16)

從而

(17)

(18)

2.2 角度α的最優區間分析

圖3 積分區間與地球自轉角α的關系Fig.3 Relationship between the integral interval and the rotation angle of the earth

因地球自轉角速度的數量級相對于速度增量很小，分母值過小會導致計算奇異[13]。所以為了提高估計精度，在分子固定的情況下盡量提高α，由圖3可知,α的最大值是在2段積分區間剛好不交錯時，即地球自轉時間與重力加速度積分時間相等

(19)

3 外部擾動誤差抑制

當船在行進過程中，由于載體受到外界環境或自身因素影響，如風浪、發動機振動等[14],使得慣導系統測量得到的地球自轉角速度和重力加速度值相對于靜基座的測量結果受到嚴重干擾，其中線振動干擾是一個重要環節[15]。

采用最小二乘算法對包含線振動干擾的速度矢量進行擬合，利用擬合結果進行姿態矩陣解算以抑制線振動干擾的影響。

由比力方程可知，對于速度模型

(20)

其中

(21)

式中，g0=9.780325。

慣性系粗對準一般在短時間內完成，這時可做如下近似

(22)

(23)

擬合后式(8)等價于

(24)

4 仿真驗證

4.1 仿真條件

為模擬艦船在航行中的真實運動情況，假設典型海況下搖擺模型為

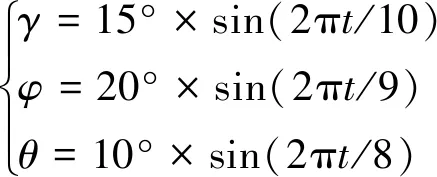
(25)

式中，γ、φ和θ分別為系統的橫滾角、航向角和俯仰角，t為時間。

設艦船初始速度為10m/s，充分考慮慣導系統的器件精度以及電磁計程儀的測量精度，仿真中各項誤差設定如所表 1示。

表1 仿真誤差設置Tab.1 Simulation error setting

4.2 仿真結果

為了檢驗優化區間后對緯度估計精度的影響，分別在緯度20°、40°、60°和80°進行仿真，截取100條次數據進行驗證(實際使用數據600s，每次讀取數據起始點都向后推5s)，啟動時間為100s。兩種積分區間選取效果對比，虛線是優化積分區間，實線是采用了原方法，如圖4～圖7所示。

改進后的緯度估計精度有了較大的提高，取100條次仿真驗證，緯度估計誤差縮小0.3°以上，估計結果如表2所示。

圖4 20°時緯度估計仿真結果Fig.4 Latitude estimation simulation results at a reference latitude of 20°

圖5 40°時緯度估計仿真結果Fig.5 Latitude estimation simulation result at a reference latitude of 40°

圖6 60°時緯度估計仿真結果Fig.6 Latitude estimation simulation results at a reference latitude of 60°

圖7 80°時緯度估計仿真結果Fig.7 Latitude estimation simulation results at a reference latitude of 80°

表2 動基座下緯度估計結果Tab.2 Latitude estimation results under the moving base

4.3 車載試驗驗證

為了進一步驗證算法的有效性，利用某型光纖捷聯慣導系統車載數據進行仿真，所用慣導系統陀螺零偏0.01(°)/h，加表零漂100μg。跑車軌跡為勻速直航，速度約為10m/s。緯度估計時間為100s，截取100條次數據進行驗證，緯度估計誤差結果如圖8所示。

經100次車載試驗誤差結果表明，采用優化的積分區間并對外部擾動誤差抑制后的緯度估計均值從0.77°縮小到0.34°，如表3所示。

圖8 緯度估計仿真結果Fig.8 Latitude estimation simulation results

表3 車載緯度估計誤差Fig.3 Latitude estimation errors in vehicle experiment

5 結論

本文對捷聯慣導系統緯度估計算法進行了優化分析，確定了最優的采樣區間。同時采用計程儀補償以及最小二乘三階擬合的方法對外部擾動誤差進行了抑制。緯度估計精度對艦船海上航行至關重要，理論仿真及車載試驗結果表明，使用以上方法可以提高緯度估計精度。