慣性系姿態確定的SINS晃動基座初始對準算法
周 月,曾建輝,劉 猛,2,馬文霞,李慧蕓
(1.哈爾濱工程大學自動化學院,哈爾濱 150001; 2.天津航海儀器研究所,天津 300131)
0 引言
當載體處于受到外界干擾(例如陣風,發動機待機和海浪等)的晃動基座初始對準時,載體的位置幾乎不會發生變化,而其角運動可以近似看作是低頻周期的搖擺運動,從而使得慣性測量單元(Inertial Measurement Unit,IMU)中陀螺儀輸出的信噪比很低,故采用傳統解析粗對準算法將無法完成捷聯慣導系統(Strapdown Inertial Navigation System,SINS)的初始對準過程[1-2]。由于其抗干擾能力較弱,傳統解析粗對準方法通常僅適用于靜基座初始對準。為了解決傳統解析粗對準無法完成的SINS晃動基座初始對準,在2000年,Gaiffe和Cottrea提出了慣性系下觀測重力視運動的初始對準思路,并應用在了法國iXSea公司的Octans光纖羅經中[3]。然而由于商業利益和技術安全,其詳細實現過程未對外進行公布,僅僅提到了通過觀測重力矢量在慣性系的視運動。對于重力視運動,如圖1所示,即隨著地球自轉,重力在慣性坐標系內做錐形運動,運動周期為地球自轉周期[4]。
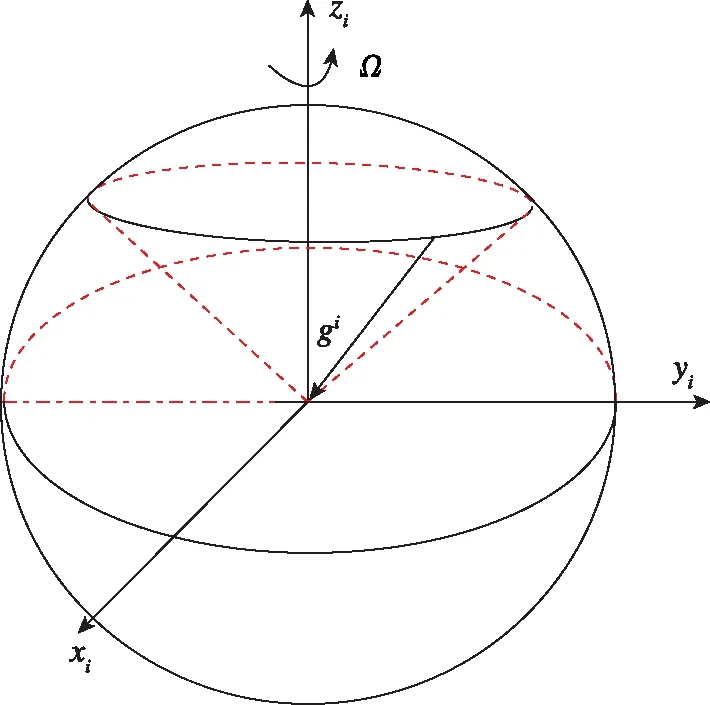
圖1 重力矢量的視運動Fig.1 Apparent motion of local gravity vector
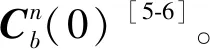
另一方面,在實施慣性系姿態確定初始對準過程中,傳統慣性系姿態確定初始對準算法通常采用直接構造重力矢量觀測來實現初始對準過程。然而由于在晃動基座自對準過程中不可避免存在的線運動誤差以及近似化誤差,將會引起矢量構造共線,從而造成初始對準過程姿態計算震蕩,降低其對準性能[12-14]。
本文首先介紹了基于Davenport-q遞歸算法的慣性系姿態確定初始對準過程的基本原理。然后,對基于重力矢量觀測的姿態確定初始對準算法在執行晃動基座對準過程中存在的問題進行分析。同時,通過分析晃動基座初始對準實際條件,提出了采用構造速度矢量觀測來實現SINS姿態確定初始對準過程,則可以充分利用積分平滑作用,抑制周期性噪聲和高斯白噪聲,從而提高其對準性能。最后,通過千島湖碼頭系泊狀態的SINS初始對準對比試驗對其進行了驗證分析。
1 慣性系姿態確定初始對準算法

(1)
式中,b(0)和n(0)分別為初始零時刻的載體坐標系和導航坐標系,其不隨時間旋轉且相對于慣性空間(i系)靜止,從而為慣性系,并稱為凝固慣性系;b(t)和n(t)分別為t時刻的載體坐標系和導航坐標系。
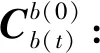
(2)
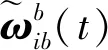
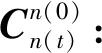
(3)
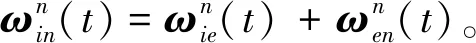
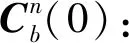
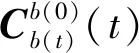
根據坐標轉換關系,易有
(4)
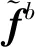
將式(1)代入式(4)可得
(5)
(6)
令
(7)
(8)
則式(6)可以重寫為
(9)
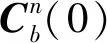
(10)
(11)
式中,M代表矢量觀測的數量;αi和βi分別為式(7)和式(8)的離散形式。
進而,式(10)的遞歸計算形式也可以給出為
(12)
(13)
2 SINS晃動基座初始對準
當載體在晃動基座進行對準時,對式(8)中的fn進行計算,根據慣導系統的比力方程可知
(14)
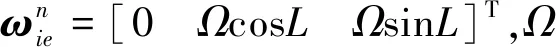
對式(6)兩邊在相同的時間區間內進行積分得
(15)
從而構造慣性系速度矢量觀測為
(16)
(17)
根據周期特性,則有
(18)
由式(18)可知,SINS晃動基座自對準過程中存在的忽略近似項,由于其具有周期特性,即使被忽略掉,也可以通過積分構造速度矢量觀測減小其對初始對準過程的影響,從而提高晃動基座初始對準的性能,則式(17)可以重寫為
(19)
3 千島湖系泊測試試驗

圖3 船艦和IMU設備Fig.3 Ship and IMU equipment
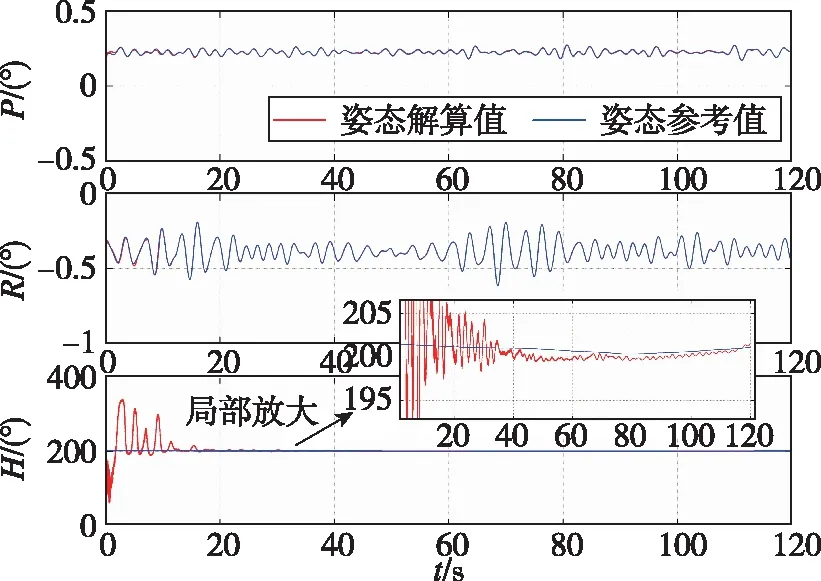
圖4 基于重力矢量觀測的SINS姿態確定初始對準過程中的姿態計算結果Fig.4 Results of attitude calculation in the process of SINS initial alignment with attitude-determination algorithm based on gravity vector observation
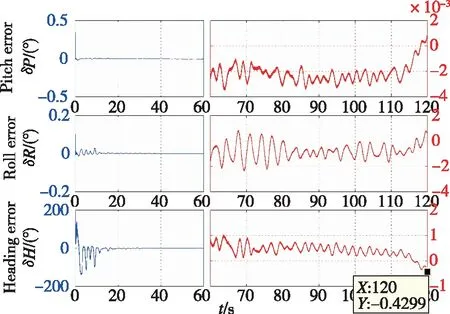
圖5 基于重力矢量觀測的SINS姿態確定初始對準誤差曲線Fig.5 The curves of alignment error with attitude-determination algorithm based on gravity vector observation for SINS
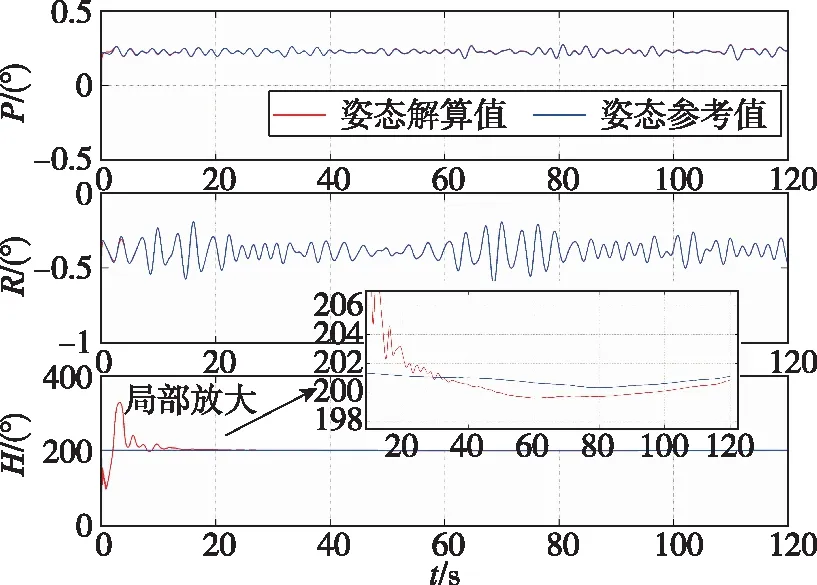
圖6 基于速度矢量觀測的SINS姿態確定初始對準過程中的姿態計算結果Fig.6 Results of attitude calculation in the process of SINS initial alignment with attitude-determination algorithm based on velocity vector observation
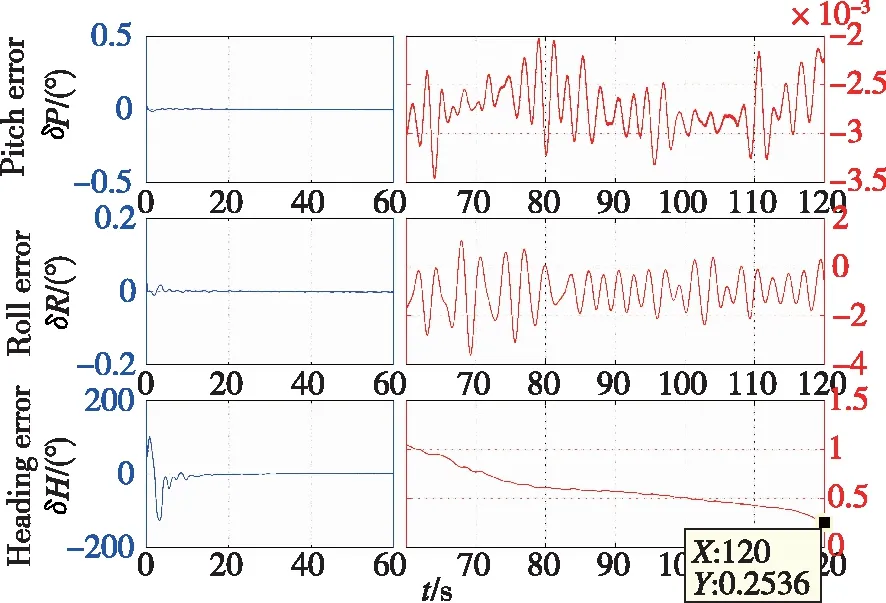
圖7 基于速度矢量觀測的SINS姿態確定初始對準誤差曲線Fig.7 Curves of alignment error with attitude-determination algorithm based on velocity vector observation for SINS
由圖5和圖7可知,慣導系統的三軸對準誤差隨時間逐漸收斂于0,故SINS慣性系姿態確定初始對準算法可以解決傳統解析粗對準在晃動基座以及受到外部干擾時所面臨的初始對準問題。另外,由圖4和圖6可知,采用Davenport-q遞歸算法完成SINS慣性系姿態確定初始對準過程中,可以實時得到載體的姿態,從而相對于傳統的雙矢量求解算法僅可以在對準結束時得到載體的姿態矩陣,其可以充分利用觀測信息,具有更優越的性能。
此外,通過對比圖4和圖6以及圖5和圖7易知,采用重力矢量觀測完成SINS晃動基座姿態確定初始對準過程,其航向對準一直存在著震蕩。但基于速度觀測矢量完成SINS姿態確定初始對準的誤差曲線更加平滑,具有更高的對準精度。這是因為在晃動基座姿態確定初始對準過程中,重力矢量觀測構造中無法避免的近似過程以及測量噪聲會造成觀測矢量的共線,進而引起初始對準過程的震蕩,從而降低SINS對準性能。而通過構造速度矢量觀測來完成的SINS晃動基座姿態確定初始對準時,其可以有效地利用積分平滑作用,進而弱化近似化過程的影響并抑制外部擾動誤差的干擾。同時在120s對準結束后,兩種算法的航向對準誤差分別為-0.4299°和0.2536°。因此,采用速度矢量觀測構造的慣性系姿態確定算法將更具優越性能。
4 結論
1)SINS慣性系姿態確定初始對準通過矩陣分解,則可以有效地隔離由外部干擾對初始對準性能的影響。為了充分利用其每一時刻的觀測信息,采用Davenport-q遞歸算法來求解其常值姿態矩陣,則可以實時求得SINS的姿態矩陣,從而具有優越的性能。
2)針對傳統直接構造重力矢量觀測的姿態確定初始對準算法在執行晃動基座對準過程中所存在的問題,通過分析晃動基座初始對準實際條件,提出了采用構造速度矢量觀測來實現SINS姿態確定初始對準過程,可以充分利用積分平滑作用,抑制周期性噪聲和高斯白噪聲,從而可以提高其對準性能。
3)通過千島湖碼頭系泊狀態的SINS初始對準對比試驗對其進行驗證。通過構造慣性系速度矢量觀測來實現SINS姿態確定初始對準算法,可以充分利用積分平滑作用,抑制外部擾動誤差的干擾,從而具有更優越的性能。

