捷聯導引頭隔離度分析與寄生回路濾波器設計

田 源，宿敬亞，王俊波

(1.北京航天長征飛行器研究所，北京 100076;2.北京電子工程總體研究所，北京 100854)

0 引言

在制導武器中，捷聯導引頭直接固聯在彈體基座上，降低了結構復雜性與成本，提高了可靠性，但該類導引頭不能直接測量制導系統所需的目標相對慣性空間的視線角速度(稱慣性視線角速度)，只能間接測量到目標相對于彈體坐標系的2個視線角(稱為體視線角)。由于載體相對于慣性空間是運動的，捷聯導引頭測量的體視線角中包含了目標相對于慣性空間的視線角和彈體姿態運動兩部分信息，需要應用陀螺測量信息對彈體的姿態進行隔離，同時解耦出制導系統使用的慣性視線角速度。目前存在兩類慣性視線角速度解耦方法：一種是間接方法，首先根據導引頭測量的體視線角信息和導航解算的載體姿態角信息構造出慣性視線角，然后對慣性視線角進行微分或濾波估計以獲取慣性視線角速度信息[1-5]；另一種是直接方法，首先根據導引頭測量的體視線角信息，采用光流法、微分網絡或濾波器等方法估計出體視線角速度，然后結合載體的姿態角速度構造出慣性視線角速度信息[6-7]。

雖然導引頭隔離度產生機理及對制導回路影響的研究源于穩定平臺導引頭，但隨著靈巧導彈的迅速發展，針對捷聯導引頭隔離度及制導回路的研究也逐漸成為熱點。隔離度是衡量導引頭輸出信號品質的一個重要指標，其表征了導引頭輸出的視線角速度對彈體運動干擾的隔離能力，而且它還會在制導回路中引入一條額外的閉環反饋回路，即隔離度寄生回路[8-9]。導引頭的隔離度對寄生回路穩定性[10-11]、控制系統穩定性[12]以及制導回路穩定性[13]均存在影響，需要合適的方法匹配慣性器件與導引頭間的性能,降低隔離度水平,并通過半實物仿真試驗等對隔離度及寄生回路的穩定性進行測試[14-15]。

本文分析了慣性視線角速度的間接解耦方法與直接解耦方法的特點，首先給出了描述捷聯導引頭隔離度的通用制導回路并推導了隔離度的表達式；然后分析了隔離度對制導回路的作用特點，提出了寄生回路濾波器的設計思路；最后通過仿真算例驗證了濾波器的有效性及其對寄生回路穩定性的影響。

1 隔離度建模與分析

由于捷聯導引頭固連安裝于彈體，只能測量目標相對于導彈彈體的體視線角，該測量信息中包含彈目視線角和彈體姿態角兩部分信息，必須利用導彈自動駕駛儀的陀螺測量信息通過數學方法解算實現對慣性視線角速度的提取及彈體運動的隔離。以俯仰通道為例，捷聯導引頭測量的幾何關系如圖1所示。其中，q為視線與慣性基準的夾角，即慣性視線角；qb為導引頭測量的視線與彈軸的夾角，即體視線角；φ為彈體俯仰姿態角。

圖1 捷聯導引頭與目標在二維平面的空間幾何關系Fig.1 Two-dimensional relative geometry for the measurement of the strapdown seeker

圖2 基于間接法的捷聯制導回路框圖Fig.2 Scheme of indirect decoupling method for strapdown guidance loop

圖3 基于直接法的捷聯制導回路框圖Fig.3 Scheme of direct decoupling method for strapdown guidance loop

(1)

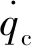
經過整理，可得

a=

(2)

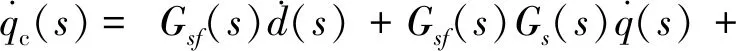
(3)

則

(4)

(5)

(6)

從式(5)和式(6)可以看出，隔離度位于制導回路傳遞函數的分母上，對于制導回路穩定性和魯棒性的影響較大。

2 寄生回路濾波器設計

寄生回路濾波器包含導引頭通道濾波器和姿態通道濾波器，其作用是調理導引頭通道的測量信號與陀螺通道的測量信號，使二者在解耦前的時頻特性匹配。令導引頭通道濾波器Gsf(s)=Gsf0(s)Gf(s)，陀螺通道濾波器Ggf(s)=Ggf0(s)Gf(s)，增加寄生回路濾波器后的捷聯制導原理框圖如圖4所示。

圖4 含寄生回路濾波器的捷聯制導回路框圖Fig.4 Scheme of strapdown guidance loop with parasitical loop filter

由式(4)所示的隔離度公式，得

R(s)=Ggf0(s)Gf(s)Gg(S)-Gsf0(s)Gf(s)Gs(s)

=Gf(s)[Ggf0(s)Gg(s)-Gsf0(s)Gs(s)]

(7)

令Δ(s)=Ggf0(s)Gg(s)-Gsf0(s)Gs(s)，則R(s)=Gf(s)Δ(s)。可見，通過濾波器設計使Δ(s)趨于0，能夠消除隔離度對制導回路的影響。理想情況下，取Gsf0(s)=Gg(s),Ggf0(s)=Gs(s)則可以使Δ(s)為0。但實際工程中無法精確獲得陀螺傳遞函數Gg(s)和導引頭傳遞函數Gs(s)，可以采取在低頻段通過系統辨識給出較為準確的模型，然后設計濾波器Gf(s)截斷Δ(s)高頻部分，使隔離度R(s)在全頻段近似為0。含制導濾波器的捷聯制導回路如圖4所示，從圖4中可以看出，濾波器設計的主要思路就是通過引入合理的濾波器使導引頭測量信息傳遞通道與姿態測量信息傳遞通道的時頻特性一致，消除信號測量與傳遞過程中帶來的噪聲干擾，確保慣性視線角速度的解耦效果。

制導回路正常工作的首要基礎就是整個回路必須是絕對穩定的，所以濾波器Gf(s)的設計還需要考慮式(5)所示的捷聯制導回路的穩定性。由自動控制原理可知，閉環系統的絕對穩定性取決于系統閉環傳遞函數的極點在s平面的分布，可以根據赫爾維茨穩定性判據對制導回路的穩定性進行分析。

3 仿真算例與分析

在實際的系統設計中，導引頭與陀螺的真實模型是高階的復雜模型，難以通過試驗數據辨識出真實的模型，但是他們的低頻特性卻可以通過試驗及測試數據建立起來。對于制導系統而言，動態性能最好的是用于姿態穩定的陀螺(例如光纖陀螺)，次之的是用于精確制導的導引頭，而自動駕駛儀的帶寬通常低于上述兩種測量設備。由于導引頭與陀螺的延時時間可以通過試驗準確測得并進行補償，在仿真中不考慮延時項。

根據圖4所示制導回路中的各環節，選取導彈某特征點處的參數建立如下模型，其中導航比N=3.5，飛行速度Vm=600m/s。

制導濾波器設計如下

本文提出的制導濾波器設計方法就是通過對導引頭以及陀螺的低頻特性進行建模，并引入匹配自動駕駛儀帶寬的低通濾波器將導引頭通道與陀螺通道的信號動態特性調整一致，從而降低制導回路的隔離度。從圖5和圖6可以看出，導引頭濾波器Gsf0(s)近似了陀螺Gg(s)的低頻特性，而陀螺濾波器Ggf0(s)近似了導引頭Gs(s)的低頻特性，而低通濾波器Gf(s)對導引頭通道與陀螺通道的信號進行了低頻截取，使得2個通道的信號能夠匹配，減小重構慣性視線角速度過程中的誤差。從圖7的隔離度頻域特性可以看出，制導回路對低頻段的姿態運動隔離效果很好。而在濾波器帶寬附近的隔離效果稍差，這是因為濾波器與實際模型的差異逐漸加大，而低通濾波器的效果還不明顯。高頻段隔離效果好是由于低通濾波器對高頻的彈體姿態進行了衰減，不會將干擾引入自動駕駛儀。圖8給出了視線角速度輸入為1(°)/s時寄生回路輸出的過載，可以看出增加了制導濾波器后寄生回路具有良好的動態特性。

圖5 導引頭濾波器與陀螺模型Fig.5 Seeker filter and gyroscope models

圖6 陀螺濾波器與導引頭模型Fig.6 Models of gyroscope filter and seeker

圖7 隔離度的頻域特性Fig.7 Characteristics of disturbance rejection rate in frequency domain

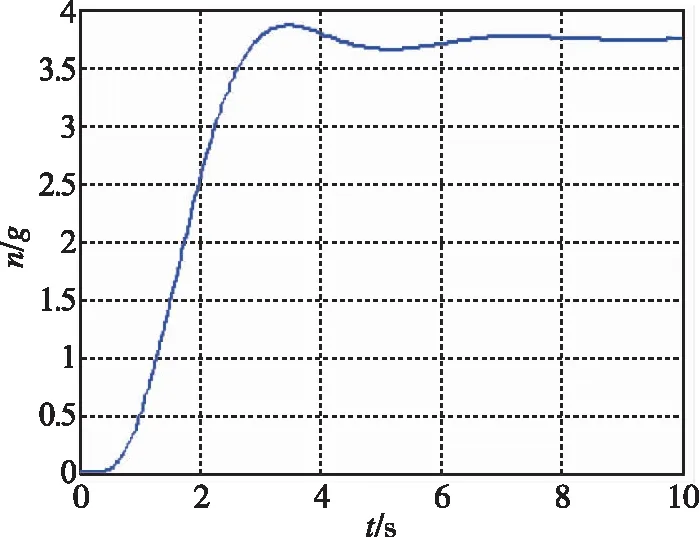
圖8 寄生回路的階躍響應Fig.8 Step response of parasitical loop

4 結論

本文分析了慣性視線角速度的間接解耦方法與直接解耦方法的特點，描述了捷聯導引頭隔離度的通用制導回路并推導了導引頭隔離度的表達式。通過對隔離度的分析提出了寄生回路濾波器的設計思路，即通過引入合理的濾波器使導引頭測量信息傳遞通道與姿態測量信息傳遞通道的時頻特性一致，消除信號測量與傳遞過程中帶來的噪聲干擾，確保慣性視線角速度的解耦效果。最后通過仿真算例驗證了濾波器的有效性，可以用于指導實際的捷聯制導回路工程設計。