基于離散余弦變換基函數迭代的人臉圖像識別

于萬波， 王香香， 王大慶

(大連大學信息工程學院，遼寧 大連 116622)

在圖像識別、圖像追蹤、視頻檢索等領域，圖像特征提取、表示與操作是關鍵技術。目前圖像特征包括顏色、紋理、形狀特征及空間關系特征等，從不同的角度反映圖像的特性與共性等[1-6]。

使用神經網絡提取圖像特征，如文獻[7]給出的深度學習(deep learning)方法具有較好的識別效果。神經網絡方法已經逐漸成為一種新的圖像特征表示方式。

基于混沌理論的圖像識別及理解也有相關文獻刊載，不過目前仍處于探索階段[8-11]。

文獻[12-13]發現一個正弦函數與一個隨機多項式函數構成動力系統，在一定的參數區間內， 混沌的概率接近 90%；在文獻[14]中，使用三角函數作為輔助函數，迭代得到圖像的近似混沌吸引子，應用于 Yalefaces數據庫，識別率達到 80%。之所以三角函數具有較好的混沌特性，是由于其振蕩且多數位置的導數絕對值較大。考慮到三角函數的這種特性，在大腦皮層柱狀結構的啟發下，嘗試用離散余弦變換基函數代替正弦函數作為輔助函數，構造動力系統進行研究。

離散余弦變換(discrete cosine transform，DCT)基函數在信號處理、圖像壓縮等領域中有著重要的應用，這其中可能存在著尚未發現的機理。

1 DCT基函數矩陣與圖像構成動力系統

1.1 DCT基函數矩陣

DCT是由基函數組合而成的。其圖像在空間中呈現出一種形似封閉的凸凹形體，且值域在[-1，1]之間，如圖1所示。

1.2 DCT基函數與圖像構成動力系統

DCT基函數記為E(u,v)，圖像函數記為G(u,v)，給定初始值，然后使用式u=z1,v=z2進行迭代，得到動力系統，即

一般當p，q與M，N約數較少，或者當p，q較大時，動力系統的混沌特性較強，序列不愿意陷入到周期點，圖 2(a)是迭代用的灰度圖像(即式(1)中的G(u,v))，圖2(b)是式(2)迭代后的軌跡(序列)點集，其中p=192，q=128；圖2(c)是當p=192，q=193時迭代后的軌跡(序列)點集；當p=192，q=128時，E(u,v)只有4個值，也就是說，最后u的值只有 4個，也只能在圖像上4條橫線上進行迭代；圖2(d)是當p=255，q=255時的序列點集。

圖1 離散余弦函數圖像

圖2 人臉圖像與不同DCT基函數的迭代吸引子

1.3 DCT基函數作用下的圖像吸引子

取Yalefaces數據庫中的N組(即N個人的)圖像，令p=253，q=251，隨機生成256個迭代初始值(點)，每個初始值迭代20次，將大于5的記載下來，得到吸引子。通過初步觀察可以發現，同組圖像的吸引子從形狀上是相似的。下節將給出具體生成吸引子以及圖像識別方法。

2 圖像迭代識別方法

2.1 圖像迭代識別方法

DCT基函數作為輔助函數的迭代識別方法：

(1) 清空內存中存儲的變量。

(2) 生成DCT基函數矩陣：①給定M，N，p，q值，計算DCT基函數矩陣E，對于常用的人臉庫，令M=256，N=256；②將矩陣E的元素調整為1到256。將E的每個元素加1然后除以2，再乘以256，取整。

(3) 讀入每組圖像并計算平均特征：①讀入 1幅圖像(適當裁剪邊緣效果較好)，用插值方法調整到256×256大小，存儲在數組G中，計算G與E迭代得到的吸引子點陣；②計算每一個圖像的吸引子點陣的二維傅里葉變換，變換后的矩陣稱為特征陣，特征存儲在數組Y(j,i, : ,:)中，表示第j組的第i幅圖像特征。計算每一組圖像的各個特征和平均值，即把每組圖像特征陣相加然后除以該組圖像個數。將特征存儲在數組Fea(jj, : ,:)中，jj表示第幾組，后面兩維表示特征。

(4) 計算要識別圖像的特征：與(3)中第一步計算每組圖像的特征相同，(重新)隨機生成k個初始值，對于每個初始值均迭代d次，將每次迭代后的(u,v)位置記載下來，存儲在數組R(:,:)中，即將R(u,v)的值設置為1，直至每個初始值都計算存儲完畢。計算R的二維傅里葉變換，存儲在數組Rfft中，這就是該圖像的特征。

(5) 計算Rfft與Fea(jj,:,:)中的每一組的特征的相關系數，相關系數最大的就認為是該組圖像，即是這個人。例如當jj=5時，相關系數最大，那么就認為該圖像是第5個人。

(6) 輸出結果：對于0≤p≤255，0≤q≤255，都能識別出160個以上，一半以上的p，q識別出165個(識別率100%)，總體識別率超過0.969 7。識別率超過了文獻[15]中的 87.21%和文獻[16]中的91.83% (使用了深度學習方法)。

實驗中每一組的所有圖像均參加訓練。另計算傅里葉變換使用Matlab中的fft2函數；計算相關系數使用Matlab中的corrcoef函數。

2.2 未參加訓練的圖像識別效果

在實驗中，待識別的每幅圖像(每組 11幅)都參加了訓練，對每組的前10幅圖像進行訓練，最多可以識別出163幅，此時p=255，q=255。若以前 5幅圖像進行訓練，那么對于165幅圖像，最多可以識別出 142幅(此時p=255，q=255)。識別率為0.860 6，只有23幅圖像沒有識別出來，平均每組有1.533幅圖像沒有識別出來。

該方法對訓練過的圖像敏感，即對于參加過訓練的圖像，識別出的概率大于沒有參加訓練的圖像。這有待于進一步分析研究。

2.3 機理分析

該方法具有較高識別率的主要原因有2個，一個是每幅圖像的吸引子是穩定的，即對于不同的初始值，當離散余弦基函數矩陣一定時，吸引子的形狀，特別是頻域特性非常穩定。例如，每組的第 7幅圖像因為比較暗，所以吸引子比較小，但是將吸引子進行傅里葉變換后，每組第7幅圖的識別效率明顯提高。盡管吸引子圖形大小不同，點集之間有微小的錯位(即混沌的初值敏感性)，但是形狀相似的圖像吸引子的頻域特性極其相似。之所以該方法對每幅圖像的記憶辨析能力極強，是因為每幅圖像特征均存儲在一個稀疏矩陣中，個性表達能力極強。

以上方法是將吸引子矩陣進行二維傅里葉變換，實際上，將吸引子矩陣投影到一維，計算一維傅里葉變換，然后計算相關系數，效果也較好。

3 CMU PIE人臉庫的識別效果

為驗證該方法的有效性，再利用人臉庫 CMU PIE進行實驗。

3.1 對于原低分辨率圖像識別

利用2.1節的方法，使用式(2)對離散余弦矩陣進行調整，即先計算其最大值、最小值，然后將矩陣調整到[0，1]之間，再乘以圖像的寬或高N(一般將圖像的寬高調整為一樣大小)。

其中，max和min分別為原DCT基函數矩陣A的最大值和最小值；B為調整后得到的新矩陣。

每張圖像進行調整，將其灰度值(利用插值方法)調整到1與N之間，有利于迭代產生質量較好的吸引子。

Pose05_64×64圖像庫內有68個人，每人49幅圖像，共3 332幅圖像。每幅圖像均為64×64大小，現使用64×64圖像直接進行識別，離散余弦基函數的M，N均取值為64。隨機生成36個初始值(點)，每個初始值迭代50次，大于40次時記錄(u,v)。對于多數p，q，識別率大于80%，每幅識別時間小于0.1 s。一半以上的p，q識別率超過83%。

統計結果見表1。

使用文獻[14]中的正弦函數作為輔助函數，用于Pose05_64×64圖像，識別率不超過0.8，說明DCT方法優于文獻[14]中的正弦函數方法。并且DCT方法更易于調整參數，可根據圖像等特點給出參數。

表1 Pose05_64×64圖像識別效果

因為特征矩陣是稀疏的，并且要進行傅里葉變換，所以計算特征時，可以求和后除以小于49的數。另外，從統計結果看，p，q是奇素數時效果好。

當p=63，q=57時，最多可識別出 1 505幅圖像，識別率達到1505/1632×100%=92.22%。

因為識別是利用動力系統的周期點分布，所以在此實驗中，當迭代次數較少時(大于2小于15)，體現的是個性，當迭代次數多于 15次時，主要記載的是圖像的共性。

3.2 插值調整到128×128大小

當把 Pose05_64×64數據庫中的人臉圖像調整到128×128時，識別效果有所提高。

表2中每組用時20 min，平均每幅用時0.073 5 s。

表2 調整分辨率后識別效果統計

未識別出的圖像如圖 3所示。其原因包括灰度、表情等，還有混沌的偶然因素，因此可用多個p，q值綜合起來進行識別。不同的p，q提取圖像特征的部位是有差別的。

圖3 未識別出的人臉圖像

人臉圖像灰度過亮或過暗時，影響迭代操作，搜索過亮平滑區域與過暗區域，以區域平均值為基礎從中間到外圍輻射狀修正灰度值，調整灰度后，識別率有較大提高。

3.3 插值調整到256×256大小

事實上，將CMU PIE數據庫中的圖像調整到256×256時，效果最好。

對離散余弦矩陣調整，再對每幅圖像進行調整，調整到[256，256，256]內。

對于Pose05_64×64數據庫，多數p，q的識別率均超過了 90%，對于 Pose09_64×64圖像庫，多數p，q均超過了95%。

在實驗中，所有圖像均參加了訓練。圖 4是Pose05_64×64數據庫的前3組圖像與1，2，3組圖像的組特征的相關系數比較圖。由于圖像數量所限，只取前3組(每組50個)為例展示。

實驗中也發現，如果不使用傅里葉變換，直接計算相關系數，那么識別率極差。說明傅里葉變換的重要性，也說明圖像的吸引子是輪廓形狀相似，但是大小以及位置并不相同。

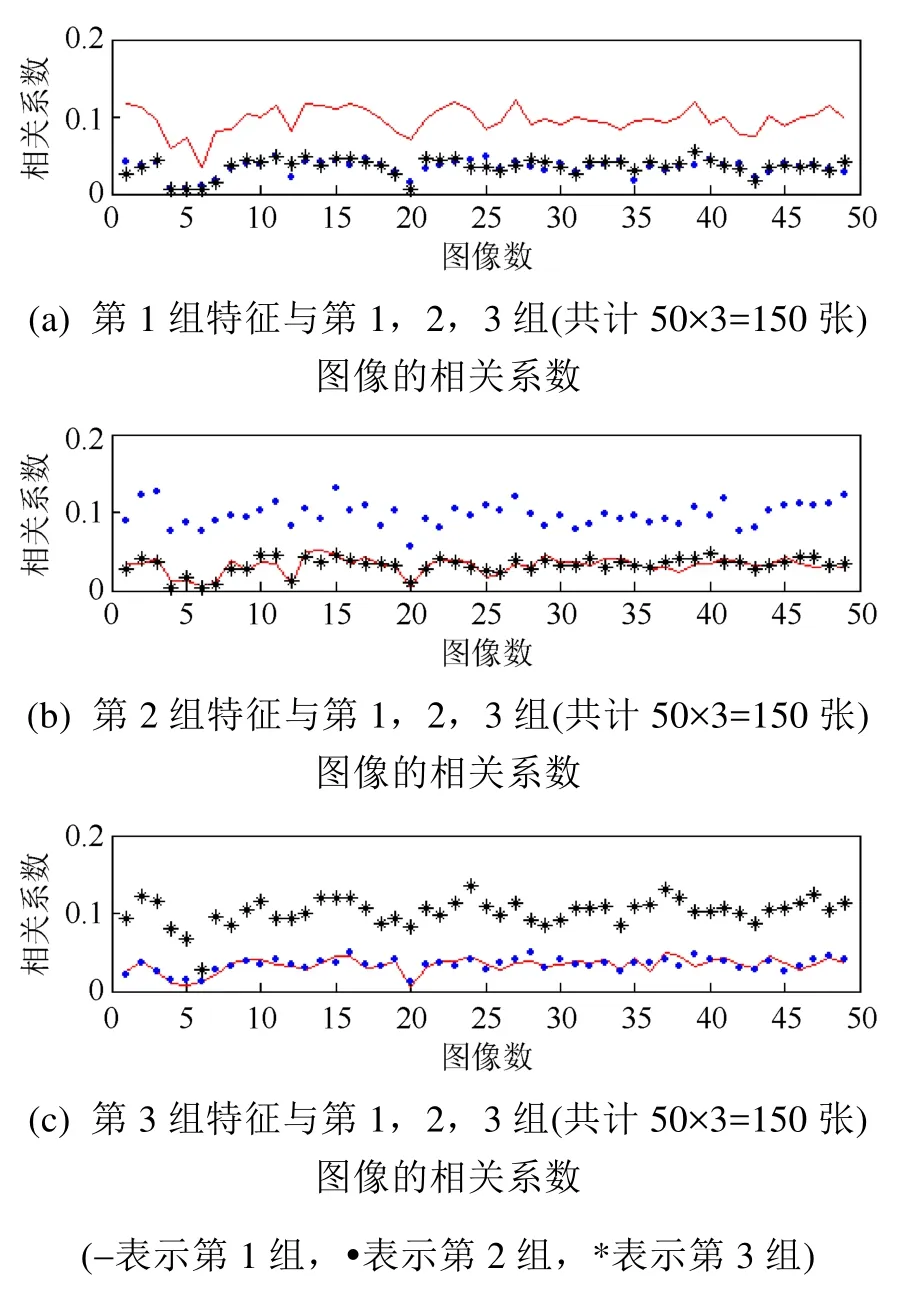
圖4 當p=253，q=249時的相關系數比較

4 結 束 語

本文利用 DCT基函數作為輔助函數與圖像函數構成動力系統，迭代產生的混沌吸引子可以作為圖像特征用于圖像識別。這是一種新的圖像特征提取方法，該方法主要是進行迭代運算，簡單、運行速度快。利用這種特征在Yelefaces數據庫以及其他人臉數據庫上進行實驗，在經過訓練的情形下，15組 165幅的Yalefaces數據庫識別率能夠達到100%，68人3 332幅圖像的數據庫識別率能夠超過99%。該結果再一次預示利用混沌描述表達復雜信息的可能性，同時這種構造混沌的方法也是混沌理論研究的一個實例。圖像混沌吸引子更大的意義可能不在于對人臉的識別，而是在于顯示了用點集(或者說利用混沌迭代)表達概念的可能性。該方法本質上與Hopfield反饋網絡相似，每次迭代得到的是不同位置上的 0，1數據，可以作為深度學習的一個階段性方法，與卷積網絡等深度學習方法結合在一起使用。