測量誤差分析及數據處理若干要點系列論文（一）
——現代數據處理基本觀念與四字要訣

林洪樺

（北京理工大學，北京 100081）

1 現代數據處理基本觀念

現代數據處理范圍廣闊，本文研究僅限于測量誤差分析方面的數據處理。隨著科技不斷發展，在當前信息化時代，數據成為科技發展的重要信息資源，數據處理的基本觀念也將隨之而作必要的適應性轉變。

1.1 數據處理目標

數據處理的目標是待求現實問題符合實際的解答。在此應用現實問題較之以往所用的實際問題是為了強調其所含有的物理本質信息。

1.2 數據處理依據

數據處理的依據是有效的樣本數據和有用的先驗信息。若要解答待求的現實問題，對樣本容量n有一定的要求。如在概率分布估計中n＜100；對于參數估計 n＜30～50；廣義而言，函數估計中 n/dVC＜20（dVC為函數VC維數）稱為小樣本，超過上述界限多視為大樣本，這些均屬經驗積累結果[1]。小樣本并未明確定義，其容量n也無確切界限。實際上所能得到的有限數據多未能全面體現現實問題的總體規律，也不滿足極限定理與大數定律的條件。可見，大多數現實數據只能屬于小樣本。小樣本自身具有隨機性，其樣本特征量也具有隨機性，難以體現其總體分布規律，尤其是對稱性，需有識別與拓展總體信息之對策。

至于先驗信息，涉及來源可靠性、主觀概率和運用方法，如貝葉斯方法等，常易被忽視。

1.3 數據處理實質

數據處理實質是對現實的模擬，以數學模型模擬現有數據及先驗信息所體現的總體規律性。故數據處理所評估與預測的結果應能夠準確地顯示最本質的總體規律。還需強調指出，實際上只要解答待求總體規律中的某種特性即可，無需求得全面的總體規律。

1.4 現實問題的性質

非線性、非平穩和非高斯/非正態統稱三非性。實質上，現實問題均具有三非性。然而，對三非性問題的處理較難且復雜，而數據處理則要求盡量簡捷，于是運用夠準的線性化、平穩化方法。唯獨現實的非高斯分布不可簡化，只能夠準地模擬，構成重點難題。

1.5 隨機性分布

隨機性分布以非高斯性分布為常態，運用統示法處理。

現代數據處理對于概率分布模式的處理，在觀念上需作相應的變化。如對于測量誤差有界性、相消性（相對期望而言）還具有普適性意義，而單峰性、對稱性則并非普適性分布規律；非高斯性/非正態性為常態（現代多稱非高斯性，下同），而高斯性只是特例；對于隨機性變量不宜說為××理論概率分布，只能說可按××分布處理；可見，為有別于具有嚴格定義的概率分布而以隨機性分布模擬之。

在現實問題中，高斯分布隨機影響因素未必占大多數，而非高斯分布的隨機影響客觀存在，隨處可見；且對非高斯分布隨機影響的統計處理方法較高斯分布復雜又難處理。非高斯分布不僅在理論分析上較難，即使在統計處理的特征量分析上，也比高斯分布僅需前二階矩要多，至少需多考慮表示偏態和峰態的三階和四階矩，甚至更高階矩。隨著數字計算機及最優化技術的廣泛應用，對非高斯分布隨機影響的統計處理不僅可實現，并已研究出許多有效而實用的統計處理方法。以往之所以多按正態分布處理主要依據中心極限定理及漸近性理論（卻難滿足其理論的條件），而更重要的還在于其簡便實用。況且，需考慮必然會存在某些重要的非高斯性先驗影響因素。總之，宜建立非高斯性應為常態的觀念。

一個值得注意的總觀念：從特殊到特殊的轉導推理[2-3]，即按所掌握的有限信息直接估計和預測出某一待求現實問題的結果，不必按傳統的從特殊到一般再到特殊的歸納演繹推理方法。如目標只是估計某一函數在某個待求點的值，就不必去估計出整個函數或其全域值；應盡量降低求解的要求，以獲得更為準確、更合乎實際的解。應用在誤差評估中，若目標只是估計誤差范圍就無需估計其理論概率分布，尤其對于小樣本很難估計出其實際總體分布。

2 數據處理對策的四字要訣

概言之，數據處理的基本任務不外乎分離其所含有的信息，即按待解答現實問題的需求，識別并提取出其中有用的本質信息，分離并擯棄其無用的無關信息（如誤差、噪聲等）。然而，不同的現實問題，其相應的數據含有信息的復雜性各異，所要求的分離技術和方法存在很大差別。顯然數據處理對策各異，對于現代數據處理可歸結出四字要訣：實、佳、智、驗，且大體上對應著數據處理的四要素：模型、準則、算法、驗證。

2.1 實——兼有真實性與實用性，尤其指模型化應合乎實際

綜觀現代數據處理無不先行模型化，即首先按所要求的準確度建立反映現實問題的數學模型。多將建模要求歸結為：實——反映現實問題所含有的本質信息；準——準確度；易——易算性；省——節省性[1]。其中實與準密切關聯，諸要求相互制約。顯然，應以實為主，若建立的數學模型不合乎實際或欠準確，其后的數據處理結果必然無效。可見，實——模型化具有真實性與實用性應為現代數據處理中最具決定性的關鍵環節，又是居首位之難點。

嚴格地說，合乎實際的模型化并非一家所能，宜由各有關專家共同建模為好。熟知，一些有用信息甚至是顯著的主要信息未必含于多次重復測量數據之中，如高準確性測量中的基準件誤差就屬于先驗信息。即僅靠數據處理還不能完整地得到實際問題含有的所有信息。然而對模型化則要求應完整地反映出實際問題所含有的本質信息，這正是模型化的主要難點。

顯然，要做到實所涉及的面廣、專業性強，非一紙可盡述。

還需強調，在數據處理全過程均需考慮做到實。經驗表明，做好以下兩點將有助于模型化合乎實際。

2.1.1 預處理

預處理目的和作用在于分析數據特性、匯集先驗信息、初定數據處理方案。

建議：1） 觀察數據圖，如坐標圖、直方圖等；2） 分析特征量，如前四階矩、分位數等；3） 檢驗異常值；檢驗對稱性，如中位值與均值重合性或零偏態性檢驗等；4） 檢驗趨勢性和周期性；5） 搜集先驗信息，通過理論分析、實驗結果、技術資料以及主觀經驗等，匯集后便可初步擬定出數據處理方案。

2.1.2 模型化具有普適性

通常可依據的可靠信息常不足以使模型化合乎實際。

建議：選用普適性模型通過適當的數據處理使之合乎實際。如對于概率分布模式采用統示法pi(x)=p(x,θi)[1]；用廣義多項式做模型化，采用逐步回歸、調整回歸、遞推回歸等可選顯著變量的方法擬合最終所用的模型[4]。

例如

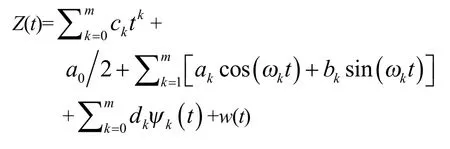
式中，Ψ(*)為特定函數；w(t)為白噪聲。

又如，數字濾波中的狀態模型

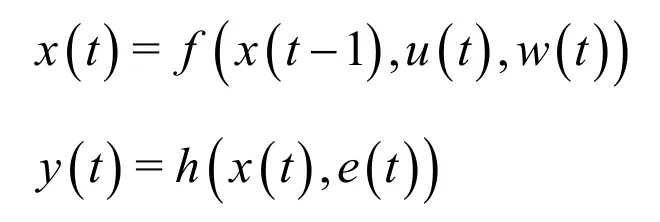
2.2 佳——數據處理應遵從最佳性原則

眾所周知，如何最終體現出數據處理具有最佳性則未必都能思考得周全。評價佳應為處理結果最逼近于現實問題或其間的誤差最小。這就涉及逼近度或誤差的量化。不同形式的量化生成各種類型的最佳準則及其相應的算法。

最小誤差類：參數估計的最小二乘、最小均方等準則，歸納為最小范數

最小風險類：Bayers統計分析的各種風險準則，如結構風險最小化準則等；

信息論方法類：基于信息熵的各種信息論方法含最大熵、最小互熵、AIC和MDL等準則。

各種最佳準則具有各自生成的理論條件，而現實問題未必完全滿足甚至不滿足這種條件，相應數據處理的最佳性就將削弱甚至失去。有些現實問題專用其最佳準則，如形位誤差評定標準規定為最小區域也即最大最小準則。可見，佳具有條件性和相對性。如均值在無粗大誤差和變量系統誤差影響下可作為測量結果的最佳估計。否則，采用其他穩健估計（如中位值或截尾均值等）則更佳[1]。

對數據處理的要求不同，佳的體現也各異。如對數據處理常有預測性要求，則其最佳性原則中就應含有泛化性或推廣性，即預測誤差要小，并非只計及對數據的擬合誤差最小。如結構風險最小原則中含VC置信范圍、驗證擬合模型的最小描述長度（MDL）準則中含數據量約束項等[1]。

2.3 智——處理方法智能化

現代數據處理中多見不適定的逆問題，且為非線性度較強、非凸性的現實問題。傳統處理方法多在求極值點原則下，算法以逐步迭代逼近為主。有諸多缺陷，如要求連續可微性；易受初始化影響；無通用性等，尤其難有全局優化性，其處理結果就未必具有最佳型。然而，多數智能化處理方法實質上是按適應度要求進行智能性全域隨機搜索，使之對優化對象無特殊限制，具有普適性；適應度可直接取實際優化目標值；智能性策略全域搜索出全局最優解；始于一組可行解，初始化影響小等。這些特點可用于解決許多難題，擴展了應用領域。

實質上，人類智能才是智能化之源泉。自上世紀中葉智能化命名以來，智能化算法就層出不窮地接連提出，名目繁多，在選用上首要考慮其全局優化性能，這也是各種智能化算法改進的重點。對于其余的性能要求無異于一般算法，如收斂性、簡捷性等，只需提醒一點，停機條件按夠準即止原則。

智還可從2方面理解：運用合適的智能化算法解決復雜難題只是其一；從當前機器學習觀念上看，進一步得出對現實問題的性能改進策略，是不可忽視的另一面。

2.4 驗——驗證處理結果的準確性

評價數據處理方法及處理結果，如模型實用性和簡約性、算法準確性和簡捷性等，均需予以驗證。驗證項目及其指標與被測量及其測量方法有關，其中最主要又是最難以驗證的應為準確度。尤其高準確度測量中常含有未引起數據變動的系統誤差因素，且多為主要成分。驗證方法頗多（以往多用理論解析、物理方法和實驗方法等），推薦采用基于MonteCarlo方法的給定誤差的數據仿真驗證方法。給定誤差的等級應與實際問題所要求的準確度相當或略高些，數據形式與所測的實際數據類同，并依據先驗信息設置已知誤差值的各種類型的系統誤差和某種概率分布的隨機誤差。對這種已知其誤差值的仿真數據也通過所擬定的數據處理方法即可驗證出處理結果的準確性。

驗證處理結果的仿真模型可擬定如下：以某一平面度測量為例

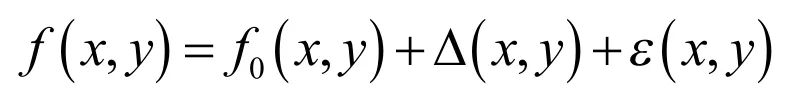
式中，f(x,y)為含已知誤差的仿真數據；f0(x,y)為理想形狀，如理想平面真值；Δ (x,y)為系統誤差，這是仿真之主項，多依先驗信息來設置，且需給定與實際問題相適應的誤差值；ε(x,y)為某種概率分布的（如β分布）隨機誤差。且可按所得先驗信息設值

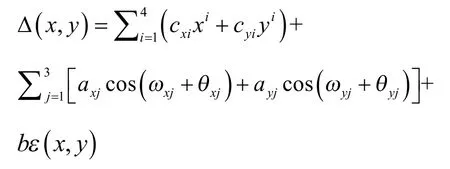
式中，cxi，cyi，axj，ayj，b及ε(x,y)宜按略高于形位誤差的準確度設定。對于已有MZ判別準則者，還可特設合乎該準則的等值最高點和最低點，并可改變其位置更利于驗證。總之，依據待求的現實問題而做具體的設置。

3 結語

“實、佳、智、驗”四字互抑；取主舍次；均衡擇優；夠準為限。

本文主要概述當前測量誤差分析及數據處理所應建立的一些主要觀念與需要作全面思考的數據處理策略。至于解決現實問題的具體方法及示例等將在此后的系列論文中陸續闡述。歡迎讀者們提出寶貴意見和建議。