基于學生作答卷面的定性學習診斷研究：以程序性知識缺失為例

朱亞平 張玉峰

摘?要：通過對學生問題解決的作答卷面分析，發現學生在問題解決過程中存在共性問題：因沒有掌握問題解決的程序性知識而導致錯誤.按照學習診斷的一般路徑，以應用牛頓定律解決問題為例，從問題描述、因果解釋、拓展整合、矯正建議等幾個方面進行學習診斷.

關鍵詞：學習診斷;問題解決;程序性知識

文章編號：1008-4134（2020）05-0011中圖分類號：G633.7文獻標識碼：B

基金項目：北京市教育科學“十三五”規劃2018?年度一般課題“基于課前學習診斷的教學整合模式研究”（課題編號：CDDB18155）.

作者簡介：朱亞平（1977-），女，江蘇武進人，本科，中學高級教師，研究方向：中學物理學科教學;

張玉峰（1973-），男，山東泰安人，博士，中學高級教師，北京市教育科學研究院基礎教育教學研究中心教研員，研究方向：物理課程與教學論.

筆者在《中學物理》2020年2月第03期的《基于學生作答卷面的定性學習診斷研究：以動量定理問題解決為例》一文中，已對學習診斷的重要性和診斷手段進行了說明，以應用動量定理進行問題解決為例闡述了如何基于學生的作答卷面側重學生對物理概念、規律的理解與應用等方面進行學習診斷.從另一個角度看，學生應用概念、規律解決問題的作答卷面不僅能反映出學生在概念、規律的理解與應用方面出現的問題，還能反映出學生在模型建構、科學推理、科學論證與質疑創新等科學思維過程中存在的問題.因此，本文以應用牛頓運動定律和動能定理解決問題的作答卷面為例，闡述如何從科學思維所需要的程序性知識角度進行學習診斷.本文的問題解決作答卷面來自某高三學生在復習牛頓定律時的一次單元測驗.

題目?質量為2kg的物體在與斜面平行的拉力F的作用下，由靜止開始沿斜面向上做勻加速直線運動，前進16m速度達到16m/s，已知物體與斜面間的動摩擦因數μ=0.25，斜面傾角θ=37°.重力加速度g取10m/s2.求拉力F的大小.

作答學生來自北京市東城區的一所示范校，該學生的物理學業成績處于全體學生的平均水平附近，作答卷面如圖1?所示.從全體學生作答情況看，出錯集中表現為不能正確列出牛頓第二定律的表達式.

1?問題描述與因果解釋

根據學生作答卷面信息，分析作答信息間的邏輯關系，推測學生可能存在的問題，并從陳述性知識、程序性知識角度分析學生產生錯誤的原因.

1.1?問題描述

從概念關聯角度看，學生能正確提取有效信息、正確分析物體受力情況，并正確計算加速度和摩擦力，也知道牛頓第二定律的內容，但沒能正確寫出合力的計算式，遺漏重力沿斜面的下滑分量，導致結果錯誤.

從問題解決思路看，該學生的解題思維路徑為：確定加速度→確定合力→確定合力與加速度的關系，是正確的.從卷面看，求合力的程序并不完整，缺少建立坐標系，分解力的環節，而學生也恰恰在求解合力時出現錯誤.正交分解法求合力的程序包括以下步驟：（1）畫出研究對象的受力分析圖;（2）確定研究對象的加速度方向，并在受力分析圖中標注;（3）在受力

分析圖中畫出直角坐標系，并將不在坐標軸上的力正交分解到兩個坐軸上;（4）列出同一坐標軸方向上合力的具體表達式.從學生列出的表達式可以看出，該名學生能判斷出合力方向平行斜面向上，知道計算一條直線上合力大小的方法——與加速度同向的力的大小減去與加速度反向的力的大小.但是該學生的作答沒有將步驟（2）和步驟（3）顯性化，表現為漏畫坐標系、將所有力分解到坐標軸上的步驟，導致合力的表達式錯誤，遺漏重力沿斜面方向的分量.

1.2?因果解釋

按照張玉峰老師提出的物理學科核心素養學習診斷內容的（3+2）×3框架，從對牛頓第二定律概念理解和解決問題的程序性知識兩個角度分析學生的錯因.

從陳述性知識角度看，學生對牛頓第二定律表達式F=ma中F的理解不深入，該表達式為矢量式，力的方向與加速度方向一致，或者說加速度的方向就是合力的方向.學生的受力分析圖中，沒有明確加速度（合力）的方向，也沒有建立坐標系，沒有將不在坐標軸上的力進行正交分解.

學生能正確計算摩擦力大小，說明他對重力進行了正交分解，知道在垂直斜面方向合力為零，只在平行斜面向上方向上有加速度.但在列牛頓第二定律方程時，遺漏了重力的分量.形式上表現為解題不規范，實際上是程序性知識的缺失，應用牛頓第二定律解決問題的程序性知識還沒有達到“規范化”階段.

用牛頓第二定律求力的程序如下：（1）確定研究對象;（2）畫出研究對象的受力分析圖;（3）確定受力分析狀態對應的加速度大小和方向;（4）建立直角坐標系，并將不在坐標軸上的力（加速度）分解到坐標軸上（一般以加速度方向和垂直加速度方向建立坐標系）;（5）分別列兩個坐標軸方向上的牛頓第二定律（或者受力平衡）方程;（6）解方程.

對于程序性知識的學習，需要將程序性知識步驟化、顯性化，學生通過記憶、模仿，按固定程序練習達到熟練水平并形成思維習慣，直至“規范化”階段.在形成思維習慣之前，必須將程序顯性化，作答過程能體現解決問題的關鍵步驟.該學生因省略建立坐標系和分解力的步驟，在求解合力時出錯，說明他在應用牛頓第二定律解決問題的程序上還需要進一步練習才能達到“規范化”階段.

2?類似問題的拓展整合

程序性知識是“如何做事”的知識.這里的“事”范圍廣泛，從完成相當固定程序的練習到解決新穎的問題，程序性知識通常以一系列要遵循的步驟的形式出現.如根據楞次定律判斷感應電流的方向，一般遵循以下步驟：（1）確定原磁場的方向及變化趨勢（增大或者減小）;（2）根據楞次定律中的“阻礙”效果，判斷感應電流的磁場方向;（3）根據右手螺旋定則判斷感應電流的方向.當任務是熟悉的練習時，學生一般知道要用什么程序性知識.如研究臺球的碰撞規律，學生能在第一時間判斷屬于動量守恒主題，應當選擇碰撞的兩個臺球為系統，列動量守恒的方程.當任務是不熟悉的問題時，學生必須確定將要使用的知識是什么.如在原子物理主題中，研究關于人工控制下的裂變反應，慢化劑中的原子核與中子相互作用，使中子減速，從而控制反應速度的問題時，學生就不能在第一時間判斷出，該過程應當選擇原子核與中子為系統，用動量守恒規律解決問題.因此理解陳述性知識是能夠運用程序性知識的前提條件.反之，程序性知識的學習過程也是促進陳述性知識深入理解的過程.

不重視程序性知識的學習，會導致學生對知識的理解不夠深入，出現能說出概念規律的內容，但在實際應用中，不能正確寫出該規律在具體物理情景中的表達式.例如，在應用動量定理解決問題時，應強調是合力沖量與動量變化的關系，而不是某個力的沖量與動量變化的關系，還應注意正確選擇研究對象并進行受力分析，找出研究過程中合力的沖量或者各力沖量的矢量和.同時，動量定理是矢量式，動量變化量也是矢量，這就要求研究一條直線上的動量變化時，一定要規定正方向，用正負號將矢量運算簡化為代數運算.不按照上述程序操作，出錯的概率會大大提高.程序性知識的缺乏或者沒有到達“規范化”階段，容易導致在運用知識解決問題過程中出錯.

3?錯誤矯正與學習建議

在物理問題解決過程中，從受力分析到牛頓定律、動量定理，從計算做功到動能定理、功能關系，從力學主題到電學、熱學主題，都涉及程序性知識的學習，不同概念規律對應的使用程序雖然在細節上有一定差異，但也有共性部分，都可以用步驟的形式表現，都與對應的概念有不可分割的聯系.下面以應用牛頓第二定律解決問題的程序性知識為例，提出錯誤矯正與學習建議.

3.1?教師示范應用牛頓第二定律解決問題的關鍵點和易錯點的正確程序

程序性知識最大的特點是能夠很容易地用動作或步驟顯示出來，表明該事是怎樣做的，但卻不容易很清楚地用語言加以描述.因此，教學中明確陳述性知識對應的程序性知識的使用步驟，尤其是關鍵步驟是極為重要的.

確定合力和加速度是應用牛頓第二定律解決問題的關鍵點和易錯點，通過以下步驟減少出錯概率：（1）畫出研究對象的受力分析圖;（2）在受力分析圖中標出運動對象的加速度方向;（3）在受力分析圖中畫出直角坐標系，并將不在坐標軸上的力正交分解到兩個坐軸上，如圖2所示;（4）列出每一個坐標軸方向上的牛頓第二定律的具體表達式.注意，合力用圖中的具體力來表示，如圖2中的牛頓第二定律方程為F-f-mgsinθ=ma.

3.2?對列式進行提問，通過解釋促進學生對牛頓第二定律的理解

在教學中引導學生對問題解決過程做出解釋或者反思是促進學生對知識深層理解的有效辦法.例如，通過“為什么用與加速度同向的力與反向的力之差表示合力”這樣的問題，促進學生對力方向與加速度方向的認識.牛頓第二定律表達式F=ma是矢量式，從方向的角度看，加速度方向與合力的方向一致，即與加速度同向的力之和一定大于與加速度反向的力之和，通過解釋促進學生領悟解決問題的程序與對應的知識是有內在聯系的.現代認知心理學認為，?程序性知識的前身就是陳述性知識，?它通常提供程序性知識所需的條件、方法、步驟、策略等信息.因此理解陳述性知識是正確運用程序性知識的前提，遇到新問題時，即使沒有熟悉的程序性知識，也可以根據陳述性知識分析出解決問題的程序.

3.3?通過變式練習，促進學生對程序性知識的理解和掌握

現代認知心理學認為，?程序性知識的學習可以分為三個階段：第一階段，?新信息進入短時記憶，與長時記憶中被激活的相關知識建立聯系，從而出現新的意義建構;第二階段是通過應用規則的變式練習，使規則的陳述性形式向程序性形式轉化，即規則開始向活動或行為的技能轉化;第三階段，規則完全支配人的行為，技能達到相對自動化.

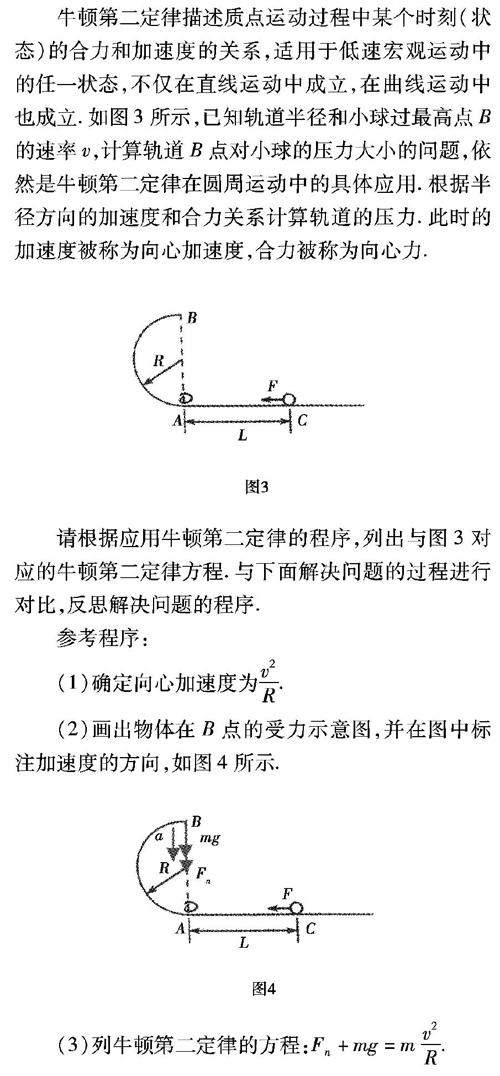
牛頓第二定律描述質點運動過程中某個時刻（狀態）的合力和加速度的關系，適用于低速宏觀運動中的任一狀態，不僅在直線運動中成立，在曲線運動中也成立.如圖3所示，已知軌道半徑和小球過最高點B的速率v，計算軌道B點對小球的壓力大小的問題，依然是牛頓第二定律在圓周運動中的具體應用.根據半徑方向的加速度和合力關系計算軌道的壓力.此時的加速度被稱為向心加速度，合力被稱為向心力.

請根據應用牛頓第二定律的程序，列出與圖3對應的牛頓第二定律方程.與下面解決問題的過程進行對比，反思解決問題的程序.

參考程序：

（1）確定向心加速度為v2R.

（2）畫出物體在B點的受力示意圖，并在圖中標注加速度的方向，如圖4所示.

（3）列牛頓第二定律的方程：Fn+mg=mv2R.

3.4?跨主題遷移練習，從陳述性知識提煉問題解決的程序性知識

借助不同主題情境，通過具體問題解決與反思過程，促進學生從陳述性知識逐漸提煉程序性知識并在實踐中靈活運用程序性知識.例如，對動能定理的應用，合力的功等于動能的變化.先對規律的表達式進行分析：關鍵量為研究對象的初態動能、末態動能以及過程中合力的功.合力功的求解往往是難點，也容易出錯，經常需要轉化為求外力做的總功的問題.具體步驟：（1）對研究對象進行受力分析;（2）確定研究過程中，每一個力所做的功;（3）計算所有力做功之和.在上述基礎上，確定動能定理的應用程序：（1）選研究對象，確定研究過程;（2）確定研究過程初末態的動能;（3）確定過程中外力做的總功.

4?結束語

在學科教學實踐中，教師進行學習診斷的依據是多方面的，包括教師的教學經驗，以及通過測試、訪談等手段獲取的實證數據.教學中應根據實際情況，靈活選擇診斷依據.本文基于學生應用牛頓運動定律解決問題的作答卷面診斷影響學生科學思維周密性的程序性知識缺失狀況.這樣的定性診斷有利于從深層挖掘學生思維過程中存在的問題并進行有針對性的矯正.

參考文獻：

[1]張玉峰.為了物理學科核心素養發展的學習診斷：概念、路徑與內容框架[J].中學物理，2020（01）：2-6.

[2]L·W·安德森.皮連生主譯.學習、教學和評估的分類學[M].上海：華東師范大學出版社，2019.

[3]梁寧建.當代認知心理學（修訂版）[M].上海：上海教育出版社，2014.

[4]楊玉東.陳述性知識與程序性知識的教學策略[J].天津師范大學學報（基礎教育版），2010，?11（03）：18-21.

[5]張玉峰.基于課前學習診斷的教學整合研究[M].?北京：北京師范大學出版社，2018.

（收稿日期：2020-01-09）