拉普拉斯變換法中的RMI原理
巴英

摘 要:拉普拉斯變換法是借助拉普拉斯變換及其逆變換,不經過通解,而是直接求解常系數非齊次線性方程(組)特解的方法。本文將站在數學方法論的角度對拉普拉斯變換法進行解析和探討,并指出常系數非齊次線性方程初值問題的解決,本質上就是RMI原理的現實演繹過程。
關鍵詞:拉普拉斯變換;拉普拉斯變換的逆變換;原函數;像函數;RMI原理;關系;映射;反演
1 前言
關系(Relationship)、映射(Mapping)、反演(Inversion)原理簡稱RMI原理,作為數學方法論范疇的一種工作原理,被頻繁地應用于數學研究和數學發現中,是分析和處理數學問題的一種非常普遍而有效的方法。
拉普拉斯變換法是工程技術上十分常見的一種計算方法,它廣泛地用于解決常微分方程、偏微分方程以及積分方程的問題中。在求解常微分方程的問題時,其顯著特點是無需先求已知方程的通解,而是直接求方程的特解,從而在運算和節奏上均得到較大簡化。
以下將從闡明RMI原理出發,僅就用拉普拉斯變換法求解常系數非齊次線性方程的過程,進行抽象出解決問題的本質過程。
2 RMI原理
2.1 RMI原理的應用過程
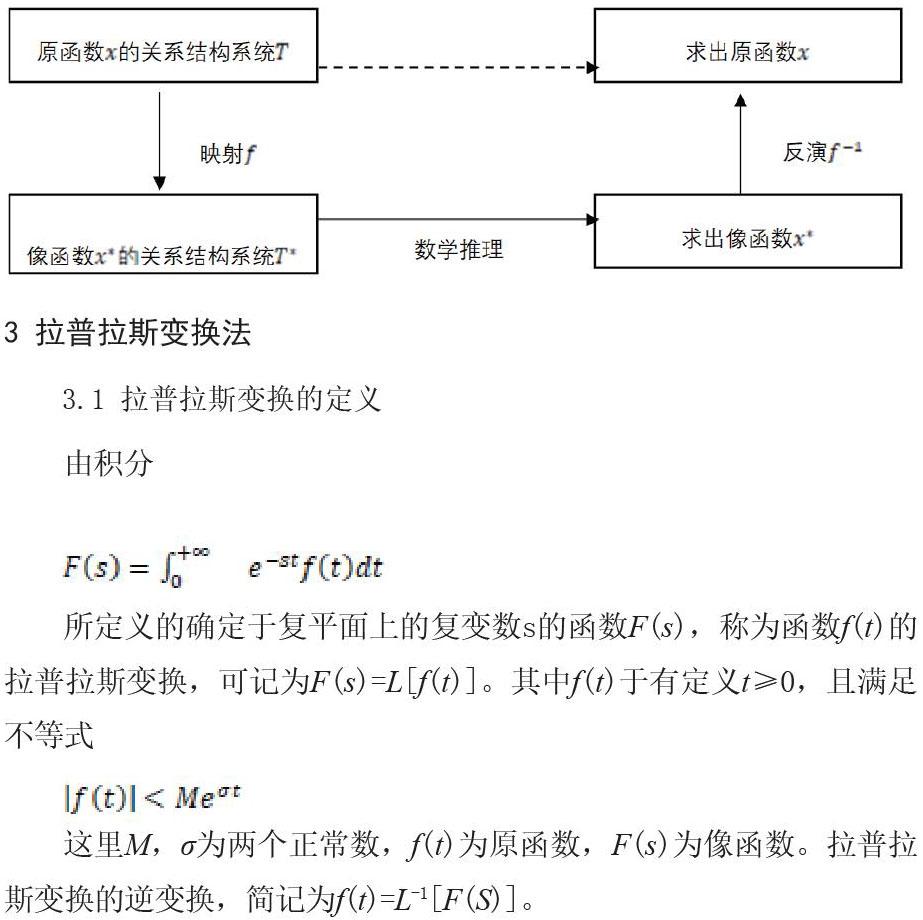
給定一個含有目標原函數x的關系結構T,如果能找到一個映射f,將T映射到T*,然后從新的關系結構T*中求出像函數x*,再通過反演即逆映射f -1將目標原函數x=f -1(x*)確定出來。
2.2 RMI原理的框架圖表示
3 拉普拉斯變換法
3.1 拉普拉斯變換的定義
再反查拉普拉斯變換表,即可得原函數x(t)。
3.3 拉普拉斯變換法的本質
讓我們同樣用一個類似的框架圖表達拉普拉斯變換法的過程,以期比較。
由此可見,用拉普拉斯變換法求解常系數非齊次線性方程初值問題的過程,本質上就是RMI原理的演繹過程。
4 結束語
RMI原理對于數學的貢獻,無論理論探討,還是實際操作,都是卓有成效的。理論上,它邏輯嚴密,無懈可擊,實際中,經常化難為易、化繁為簡,能夠簡單迅速地解決問題。總而言之,RMI原理是一個值得我們反復探尋的永恒課題。
參考文獻
[1]王高雄等.常微分方程(第三版)[M].高等教育出版社.2006
[2]E.卡姆克.常微分手冊[M].高等教育出版社.1977.
[3]鄭隆,毛鄂.數學思維與數學方法論概論[M].華中理工大學出版社,1997.

