基于應力分布模型的隨機疲勞加速試驗設計

穆童，孟鴿，謝里陽,*，張建波，石朝成

1. 東北大學 機械工程與自動化學院，沈陽 110819 2. 航空動力裝備振動及控制教育部重點實驗室，沈陽 110819 3. 上海航空材料結構檢測股份有限公司，上海 201210

早在19世紀，人們就已經認識到了材料的疲勞問題，W?hler在1860年就繪制出了最早的S-N(應力-壽命)曲線[1]。此后，對疲勞問題的研究逐步深入。目前，在常規疲勞問題的研究方面已經形成了較為完善的理論體系。但是，振動疲勞的研究則起步較晚，直到1958年，美國學者Crandall將振動與疲勞問題結合起來[2]，從此人們才真正開始關注到振動疲勞問題。1963年，Crandall和Mark將振動疲勞定義為結構在振動激勵下產生的響應所造成的可以累加損傷的強度破壞[3]。

在疲勞壽命預測問題上，工程中常用的求解方式主要有2種，即時域分析和頻域分析。日常對各種物理量的認知普遍是從時域角度出發的，表述時以時間作為橫坐標，體現出了物理量在一定時間范圍內的變化情況；而頻域方法表達的則是物理量與頻率之間的關系。相比之下，簡單的、規律性的變化用時域求解方式較為直觀、準確，而當面對一些復雜的或隨機的載荷時，頻域求解方式則能更加清晰明了地表達載荷特征，且求解速度更快。

在振動疲勞壽命預測理論模型方面，Bendat和Piersol于1966年率先提出了使用功率譜密度直接計算疲勞損傷的方法，其計算方法基于窄帶隨機過程的特點，使用功率譜密度函數估計隨機應力的幅值分布，進而計算出結構的疲勞損傷[4]；但是Bendat的研究是在窄帶隨機過程的基礎上進行的，而實際工程中的隨機振動普遍是以寬帶分布的形式存在的，若直接使用則會出現較大誤差。Wirsching等在Bendat的研究基礎上進行了修正，提出了新的計算模型[5-6]。此外，Chaudhury和Dover也基于Bendat所提出的計算模型進行了修正[7]。1985年，Dirlik使用了計算機模擬的方式對寬帶隨機過程的幅值分布進行了擬合，總結出了一個適用于寬帶分布的經驗公式[8]，該公式對于帶寬的敏感性低，在實際使用時具有比其他模型更高的精度，因此應用較為廣泛。Benasciutti和Tovo同樣在其研究中提出了一個適用于寬帶隨機過程的幅值分布模型，并且也具有較高的擬合精度[9]。

1 隨機振動疲勞理論

1.1 隨機過程

隨機過程可分為平穩過程與非平穩過程，生活中常見的一般為平穩隨機過程，該條件下反映隨機過程x(t)在t1時刻自身前后相關性的自相關函數Rx不隨時間變化[10]，即

Rx(t1,t1+τ)=Rx(τ)=E[x(t)x(t+τ)]

(1)

式中：E為期望；t為時間；τ為時間間隔。

自相關函數在時域內描述了隨機過程的統計特征，而在頻域內描述隨機過程用的則是功率譜密度函數(Power Spectral Density，PSD)，二者組成一個傅里葉變換對[11-12]：

(2)

(3)

式中：Sx(ω)為功率譜密度函數；ω為圓頻率。

值得注意的是，功率譜的定義區間為正負2個實數域，稱作雙邊功率譜，而現實中不存在負頻率，因此定義單邊功率譜密度Gx(ω)為

(4)

此外，除了可以通過自相關函數定義隨機信號的功率譜密度外，還可以通過濾波法與快速傅里葉變換法來定義功率譜密度，公式分別為

(5)

(6)

式中：y(f,t,b)為濾波后中心頻率為f、時間長度為t、帶寬為b的信號的幅值；fft為對信號進行快速傅里葉變換。

快速傅里葉變換法即為將時間長度趨于無限的隨機信號通過傅里葉變換完成從時域到頻域的轉換。

基于信號的功率譜密度，定義平穩隨機過程的譜矩mi為

(7)

其各階譜矩在時域內的意義為[13]

m0=E[x2(t)]

(8)

(9)

(10)

定義了譜矩之后，可用各階譜矩來表達隨機過程的一些特征，如隨機過程的均方根值σRMS:

(11)

隨機過程的均方根值是均方值的開根，均方值代表了功率譜密度曲線與橫軸包圍的面積，面積越大，說明隨機譜的能量越大，因此隨機振動的均方值和均方根值在某種意義上表明了隨機振動的強弱，二者越大說明振動越強。

引入不規則因子γ來描述隨機過程的不規則性，其公式為

(12)

不規則因子的取值范圍為[0,1]，當其取值趨近于1時，即意味著在時域歷程中幾乎每次正向穿越零水平后都會對應出現一個波峰，也就意味著此時隨機過程為窄帶隨機過程，當γ=1時，隨機過程則變成了簡單的簡諧波；相反地，當不規則因子趨近于0時，隨機過程也隨之趨近于寬帶過程，當γ=0時，隨機過程為白噪聲。

另外，帶寬系數ε也可以衡量隨機過程為寬帶還是窄帶過程：

(13)

與不規則因子相反，當帶寬系數趨近于1時，隨機過程趨近于寬帶過程，反之則趨近于窄帶過程。

反映單位時間內峰值次數的峰值期望率Vp[14]為

(14)

反映單位時間內正向穿越均值的正斜率穿越期望值V+為

(15)

1.2 隨機疲勞

頻域疲勞壽命預測，廣泛應用于解決結構承受隨機載荷時的疲勞問題。經典疲勞理論是建立在應力或應變的時域分析基礎之上的，主要思路為對零部件工作狀態中的危險點進行應力應變時間歷程的求解，結合Miner準則與響應歷程中的循環次數來計算累積損傷量，從而推算出預估的疲勞壽命；而頻域疲勞分析方法的基本思想則是從載荷的功率譜密度等統計特征出發，通過傳遞函數求解出零部件危險點的響應應力應變的統計特征，并根據這些統計特征估算出各水平的應力在單位時間內的期望循環次數的概率密度函數，然后使用Miner準則從統計學角度求出疲勞損傷的期望值，最終完成疲勞壽命的預測。時域方法能夠清晰明了地反映出結構的壽命周期中的受載過程，可將加載順序等頻域方法無法考慮到的因素考慮進來，壽命預測更為精準，但疲勞分析時域方法的計算量非常大，計算起來難度較大；而頻域分析方法的切入點則是載荷的統計學特征，該方法無法準確地描述應力應變歷程，只能通過統計學的方式計算疲勞損傷，因此準確性上要低于時域方法，但其優勢在于計算量小，求解速度快，更加適合工程應用。

根據Miner準則可知，應力應變每循環一次都會造成一定損傷，不同大小的應力應變將造成不同程度的損傷，當累積損傷量到達一定值時，零件將會發生疲勞失效[15]。S-N曲線中某應力幅S對應的疲勞循環次數為N(S)，該水平應力在某時段內實際的循環次數為n(S)，規定零件總損傷量為1時發生疲勞失效，則這一時段內該水平應力造成的損傷量D為[16-19]

(16)

式中：N(S)可以由材料疲勞曲線的表達式獲得，工程上常用的疲勞曲線冪函數公式為

SmN=C

(17)

其中：m與C均為材料常數；N為疲勞壽命對應循環數。

若某工況下應力為連續分布，則時間t內幅值在(S,S+ΔS)的應力循環次數可以記為

n(S)=vtp(S)ΔS

(18)

式中：v為單位時間內所有應力雨流幅值循環次數；p(S)代表幅值為S的應力分布密度；ΔS為應力區間。因此，連續分布的應力幅造成的疲勞損傷為

(19)

則用時間表示的零件的疲勞壽命tL為

(20)

由此可見，要想在頻域范圍內合理預測零部件的疲勞壽命，需要了解響應應力的幅值分布情況，即式(20)中的p(S)，而這正是頻域疲勞方法的重難點所在，目前的研究中最為常用的是Dirlik應力幅值分布模型。

Dirlik使用蒙特卡洛方法在計算機中建立了時域模擬信號，對大量不同不規則因子的PSD曲線進行了模擬仿真，總結出了一套經驗公式。Dirlik將幅值范圍概率密度函數假設為了一個指數分布與2個瑞利分布的和，公式為

(21)

式中：

Dirlik法是頻域疲勞壽命預測研究中使用最廣泛的方法，對于大部分寬帶隨機過程都有很好的適應性，因此工程中一般采用該模型進行隨機振動疲勞壽命預測。雖然其只是經驗公式，沒有理論支撐，但在絕大多數情況下，都有比其他模型更好的計算精度[12-14,16-20]。

以目前的研究與應用來看，多數研究人員將頻域幅值分布模型直接應用在了單一S-N曲線表達式所描述的應力分布區間內，但使用基于Dirlik等模型的頻域方法時，計算出的應力幅分布區間寬泛，而且會有大量的小幅值應力出現。對于一些常用的碳鋼、合金鋼、高強鋼等材料，其S-N曲線在雙對數坐標系下會出現明顯的拐點，如果用單一的S-N曲線表達式來描述其疲勞性能將導致一部分應力幅值對應的損傷出現一定的誤差，降低了壽命預測模型的準確度。因此在使用頻域幅值分布模型時，可以采用分段計算疲勞損傷的方法，這樣將得到更加精確的計算結果。

在考慮超高周疲勞的影響時，大部分材料的S-N曲線將呈現出三段甚至更多段的形式[21]，此時如果使用單一冪函數擬合的S-N曲線將會存在明顯的精度問題，顯然也應該分開計算疲勞損傷。本文僅以兩段式S-N曲線進行說明。

使用雙對數坐標系下的2條直線來擬合S-N曲線，其表達式為

(22)

式中：下標a、b用以區分兩段表達式參數;S0為兩段表達式的分隔點。

此時零件的疲勞損傷表達式為

(23)

對應的疲勞壽命為

(24)

2 加速試驗

在機械裝備產品的研發過程中，可靠性試驗是不可或缺的一環。在產品前期的設計研發階段中，一般需要對產品的可靠性及壽命進行預估，并在之后通過可靠性試驗的方式對其進行驗證。通常來講，機械產品的疲勞壽命普遍較高，如果將其按照正常的工作應力水平進行壽命試驗，需要很長的時間，因此可以在試驗時適當提高激勵水平，使結構工作在比正常工況更加嚴酷的環境中，達到更早地出現失效的目的，以此節省大量的試驗時間。在試驗結束后通過等效關系便可推算出正常應力水平下的工作壽命，這一試驗方法即加速壽命試驗。

2.1 基于Dirlik模型的加速等效關系

除使用隨機響應分析直接求解結構的響應功率譜密度外，工程上也會使用結構的傳遞函數來得出危險點的應力功率譜密度。在合理范圍內，當外載荷的施加形式、位置、方向沒有變化時，結構的傳遞函數只取決于結構本身，而與載荷大小無關。某點的響應應力PSD與在某特定位置處施加的激勵PSD之間的關系為[20]

(25)

式中：Gb(f)為結構上b點的響應應力功率譜密度函數；Wa(f)為施加在結構a處的激勵功率譜密度函數，其形式不限，可以為集中力、基礎運動等；Hba(f)則為結構在a點處承受激勵時b點的頻響函數，即傳遞函數。

由式(25)可知，在一定合理范圍內，當結構所受的激勵增大時，危險點處的響應也隨之線性增大。當激勵點處的激勵PSD的幅值W′a(f)變為原有幅值的k倍時，危險點b處的響應應力PSD即G′(f)將同樣變為原有的k倍，而根據式(7)中的譜矩定義，各階譜矩的變化情況為

(26)

隨機過程其他參數的變化情況為

(27)

(28)

(29)

(30)

(31)

式中：上標′表示變化后的變量。對于Dirlik模型來說，當響應應力PSD的幅值G′b(f)為原有幅值的k倍時，模型中各參數的變化情況為

D′3=1-D1-D2=D3

則此時應力幅值的概率密度函數為

(32)

單位時間內的疲勞損傷為

(33)

可推導出使用不完全gamma函數表達的基于Dirlik模型的損傷比例j損傷表達式為

(34)

因此壽命之間的比例關系j壽命為

(35)

其中:

式中：Γ(·)為上不完全伽馬函數；γ為下不完全伽馬函數。

2.2 算 例

某吊掛結構局部如圖1所示，查詢機械工程材料數據手冊得知，該結構所用材料的S-N曲線散點數據如表1所示[22]，可以看出該材料的S-N曲線在疲勞極限附近出現了明顯的拐點，如果用一條直線對其進行擬合則效果較差。忽略各修正系數的影響，使用雙對數坐標系下的兩條直線對材料的疲勞特性擬合情況如圖2所示。

圖2中所對應的兩擬合線的表達式為

對該結構給定如圖3所示的y方向寬帶隨機加速度載荷，該載荷與GJB150A中所給出的噴氣式飛機外掛設備振動載荷相一致[23]。使用有限元分析得到危險點的位置如圖1所示，其響應Mises應力功率譜密度如圖4所示。

由圖4曲線可以看出，該結構的響應應力PSD有多個尖峰，屬于寬帶隨機過程，使用Dirlik模型可以較好地擬合出應力幅值的分布。基于該模型，使用式(24)求解出該結構危險點的疲勞壽命為5.468×107s。

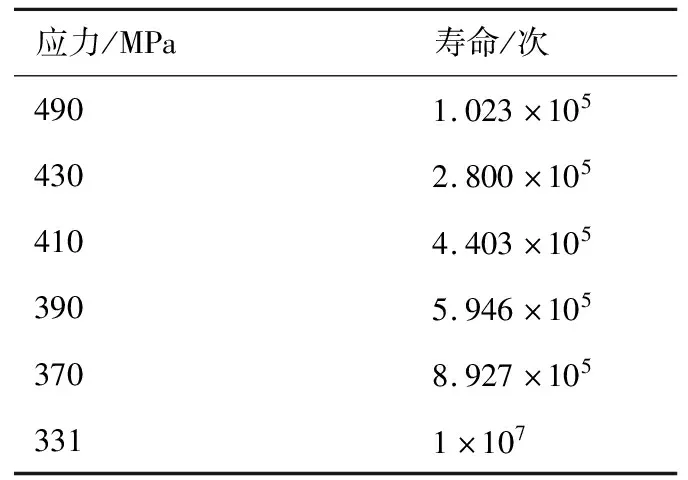
表1 材料S-N曲線散點[22]

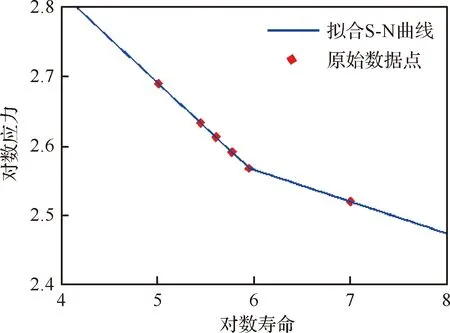
圖2 S-N曲線擬合結果

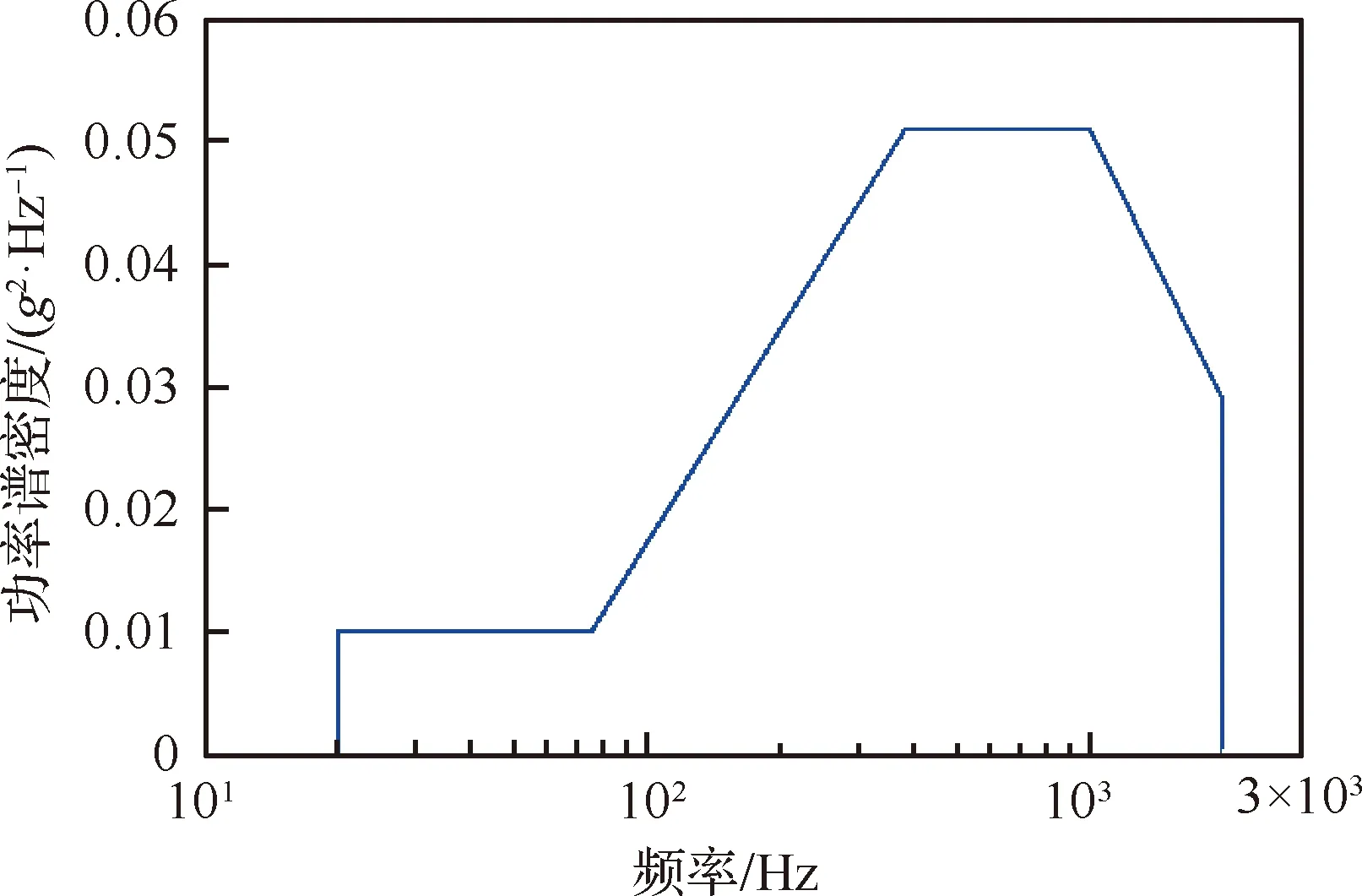
圖3 輸入加速度功率譜密度

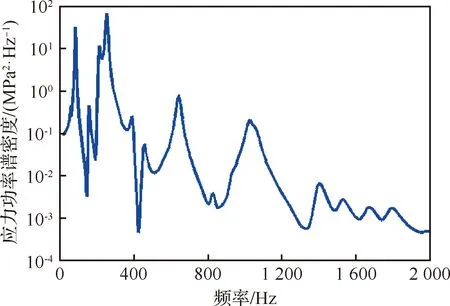
圖4 危險點響應應力功率譜密度

將該點的響應PSD數據與材料疲勞性能數據代入式(35)中，使用MATLAB繪制出激勵與壽命放大倍數之間的加速關系如圖5所示，其中橫坐標表示激勵PSD的放大倍數，縱坐標表示壽命的放大倍數。從圖中可以看出，曲線大體呈兩段直線走向。

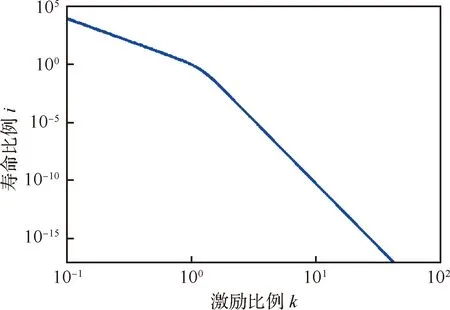
圖5 激勵與損傷的等效關系

不難理解這一規律，當施加在結構上的隨機載荷由小變大時，也就意味著有更多的大幅值應力出現，即落入圖2所示S-N曲線左段的應力幅占比越來越大，因此在激勵比例增加時，壽命將以更快的比例衰減，也可以說，圖5中的右半段直線對應了所使用的S-N曲線高應力部分，左半段則對應了低應力部分；而如果使用一條直線對S-N曲線進行表征，則這一等效關系也將變為一條直線，即激勵與壽命呈對數線性關系，此種情況下與他人現有的研究結論保持一致[20]。Clevenson和Steiner曾經對一批2024-T4鋁合金試件進行了多次隨機振動疲勞試驗，研究各種載荷參數對壽命的影響，針對2個不同形狀的PSD，在一定范圍內改變一組試樣所受載荷大小，得到了不同均方根值下的壽命如表2[24]所示，將數據繪制在雙對數坐標系內如圖6所示。

圖6中，2條折線分別是根據2個PSD在各級載荷水平下的對數壽命均值點連線所得，曲線1與數據1對應中表2中載荷均方根1列的數據，曲線2與數據2對應表2中載荷均方根2列的數據。可以注意到2組數據均呈現出較明顯的線性特征；同時，在2條折線的左上方均呈現出了一種向下彎折的趨向，同圖5中的曲線特征保持一致，從而證明了該方法的正確性。

表2 文獻[24]試驗數據

圖6 加速試驗結果

另外，一般加速試驗需要提高應力水平來縮短試驗時間，即對應圖中k>1的部分，可以看出，這一段曲線既有后續呈現線性的部分，也有兩段曲線的過渡部分，因此針對零部件結構上這一點的加速關系不能用簡單的對數線性來表達。需要注意的是，假設該算例中其他條件均不變，增大原有載荷PSD的幅值，則須將曲線整體向左移，此時k>1的部分可按照對數線性近似處理；反之，需要將曲線向右平移，此時k>1的部分同時包含了曲線中兩段呈直線的部分，這樣則不能簡化處理。

由討論可以看出，在進行基于頻域疲勞模型的加速試驗時，加速關系不僅僅取決于材料性能，還與零部件所承受的載荷有關，如果按照一般的對數線性關系來計算的話，可能會出現較大的誤差。

3 結 論

1) 針對隨機振動中小應力循環占比較大的情況，將Dirlik雨流幅值分布模型應用到了雙對數坐標系下的2段直線所表征的S-N曲線上，該求解思路使得頻域方法更加適用于隨機振動疲勞問題，且該方法還可以拓展到多段直線所表征的S-N曲線的情況中。

2) 基于所提出的多段式S-N曲線的求解思路，以2段的情況為例，推導了使用Dirlik模型為基礎的振動疲勞頻域求解方法支撐下的加速應力等效關系式，總結出了加速壽命換算方法，為振動疲勞的加速試驗提供了理論支持。

3) 算例表明，在使用雙對數坐標系下的2條直線對S-N曲線進行表達時，所推導出的應力與損傷放大倍數的等效關系近似為2段對數直線關系，并借助相關文獻中的試驗數據對方法進行了驗證。