基于非線性Wiener過程的航空發(fā)動機性能衰減建模與剩余壽命預(yù)測
王璽,胡昌華,*,任子強,熊薇
1. 火箭軍工程大學(xué) 導(dǎo)彈工程學(xué)院,西安 710025 2. 國防大學(xué) 聯(lián)合勤務(wù)學(xué)院,北京 100089
航空發(fā)動機作為飛機的“心臟”,不僅為飛機提供動力,同時也為航空事業(yè)的發(fā)展注入強大動力。然而,航空發(fā)動機由于長期運行在復(fù)雜多變的惡劣環(huán)境下,其性能會隨之產(chǎn)生衰減,并在累積到某種量級時,導(dǎo)致發(fā)動機失效[1]。目前,航空發(fā)動機在航空領(lǐng)域發(fā)揮著重要的作用,一旦發(fā)生由失效引起的事故,所造成的后果將難以估計。因此,通過監(jiān)測的航空發(fā)動機性能衰減數(shù)據(jù),建立相應(yīng)的性能衰減模型,進而實現(xiàn)航空發(fā)動機的剩余壽命(Remanining Useful Life,RUL)預(yù)測是近年來熱門的一項關(guān)鍵技術(shù)[2]。然而,航空發(fā)動機的壽命有多種定義,如首翻壽命、大修壽命、總壽命等,同時又受多種因素約束,如性能衰減、關(guān)鍵件壽命等。鑒于此,本文主要研究的是在首翻壽命的定義下,基于性能衰減建模的航空發(fā)動機剩余壽命預(yù)測。
目前,基于性能衰減建模的剩余壽命預(yù)測方法已經(jīng)廣泛地應(yīng)用于航空發(fā)動機[3-5]、導(dǎo)彈[6-8]、電機[9]等。例如,黃亮等[3]基于多階段Wiener過程建立了航空發(fā)動機的性能衰減模型,通過融合發(fā)動機的歷史性能衰減數(shù)據(jù)和實時監(jiān)測數(shù)據(jù),實現(xiàn)對發(fā)動機的剩余壽命預(yù)測。王浩偉等[6]針對導(dǎo)彈多個部件間的競爭退化,綜合考慮了退化失效和突發(fā)失效2種競爭模式,提高了對導(dǎo)彈剩余壽命預(yù)測的精度。袁慶洋等[9]針對電機的退化特性,建立了多段Wiener過程模型,實現(xiàn)了電機的剩余壽命預(yù)測。
然而,對于航空發(fā)動機這類復(fù)雜的機械系統(tǒng),在性能衰減過程中普遍存在著三源不確定性,即時變不確定性[10]、個體差異不確定性[11]、測量不確定性[12]。時變不確定性是指性能衰減過程隨著時間變化的固有不確定性;個體差異不確定性是指同類型設(shè)備之間的性能衰減差異,即同類型設(shè)備的不同個體在性能衰減過程中雖然具有相似的衰減路徑,但實際的衰減率是不相同的;測量不確定性是指測量的性能衰減數(shù)據(jù)與實際的性能衰減狀態(tài)之間的差異。在實際中,由于受噪聲、干擾、儀器精度等影響,想要對性能衰減狀態(tài)的精確測量幾乎是不可能的,因此測量中難免會引入測量誤差,造成測量的不確定性。
目前,有關(guān)同時考慮三源不確定性的研究較少。為此,文獻[13]基于線性的Wiener過程建立了同時考慮三源不確定性的性能衰減模型,并使得預(yù)測的剩余壽命分布可以隨著性能衰減數(shù)據(jù)在線更新。然而,對于航空發(fā)動機而言,在性能衰減過程中不僅具有三源不確定性,還具有強非線性。鑒于此,文獻[14]在非線性下考慮了三源不確定性,并且證明了同時考慮三源不確定性可以有效地提高剩余壽命預(yù)測的精度。文獻[15]在此基礎(chǔ)上,利用粒子濾波實現(xiàn)了對鋰電池的剩余壽命預(yù)測。但是,以上有關(guān)考慮三源不確定性的工作中存在一個共性問題,即假定有多組同類型設(shè)備的歷史性能衰減數(shù)據(jù)來離線地辨識模型初始參數(shù),并且這些參數(shù)一旦確定,就不再隨著新的性能衰減數(shù)據(jù)進行更新。因此,剩余壽命預(yù)測的精度受限于數(shù)據(jù)量,并且預(yù)測的結(jié)果在很大程度上依賴于選擇的模型初始參數(shù)。然而,針對新研發(fā)的航空發(fā)動機,往往是缺乏此類相關(guān)的歷史性能衰減數(shù)據(jù)和先驗信息,因此,以上方法具有一定的局限性,且目前相關(guān)的研究較少。
對于目前航空發(fā)動機剩余壽命預(yù)測存在的問題,本文建立了同時考慮三源不確定性和非線性的性能衰減模型,并在首達(dá)時間下推導(dǎo)出剩余壽命的分布。然后,針對新研發(fā)的航空發(fā)動機,提出了一種基于Kalman濾波和條件期望最大化(Expectation Conditional Maximization,ECM)算法的參數(shù)估計方法,以克服缺乏歷史性能衰減數(shù)據(jù)和先驗信息的問題,并當(dāng)新的監(jiān)測數(shù)據(jù)可用時,能夠自適應(yīng)地估計模型參數(shù),進而更新剩余壽命的分布,實現(xiàn)了對新研發(fā)航空發(fā)動機剩余壽命的在線預(yù)測。最后,通過實例驗證了本文方法可以有效地提高預(yù)測的精度并降低預(yù)測的不確定性,且更加適用于新研發(fā)的航空發(fā)動機。
1 模型描述
針對航空發(fā)動機在性能衰減過程中存在的非線性和不確定性,本文采用一類一般性的非線性Wiener過程來建模航空發(fā)動機的性能衰減過程。具體地,性能衰減過程{X(t),t≥0}由標(biāo)準(zhǔn)Brown運動B(t)驅(qū)動,可以表示為
(1)


Y(t)=X(t)+ε
(2)

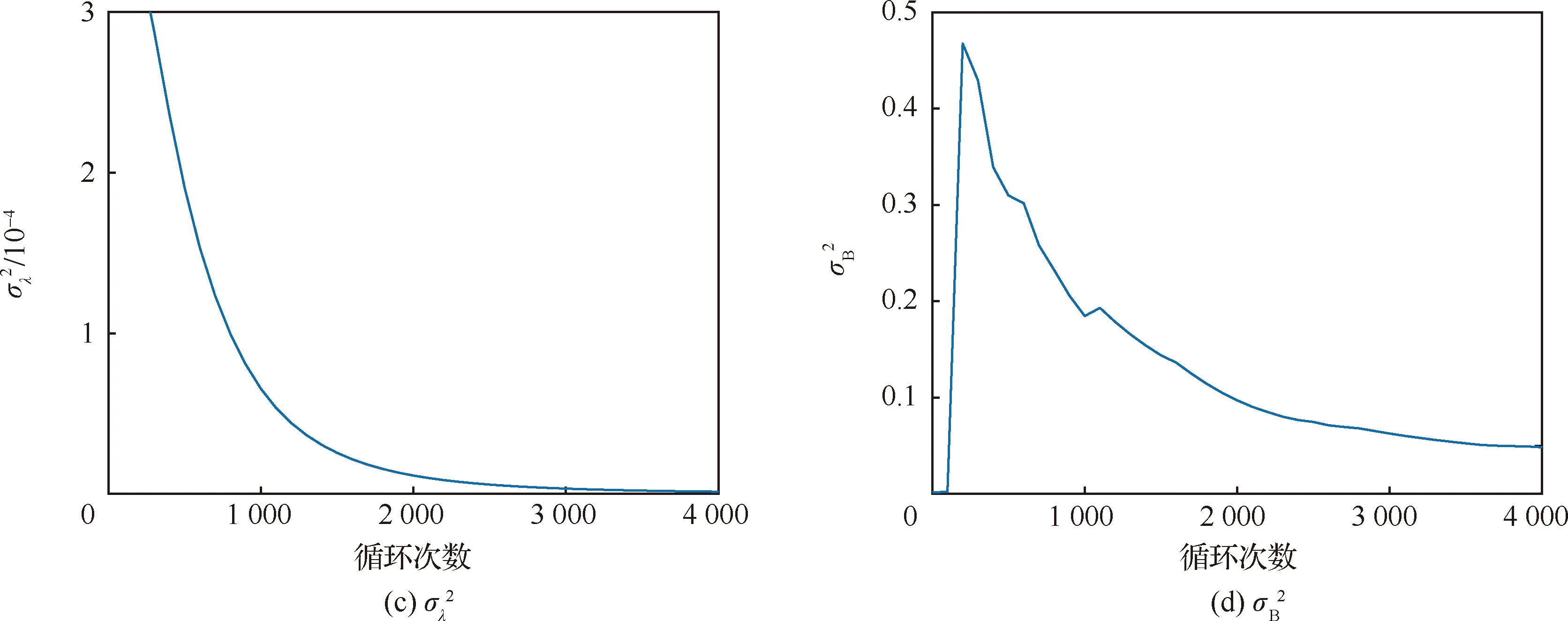
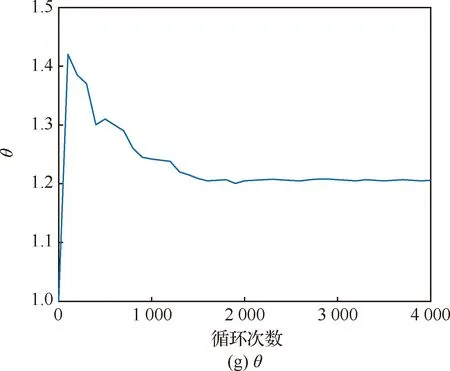
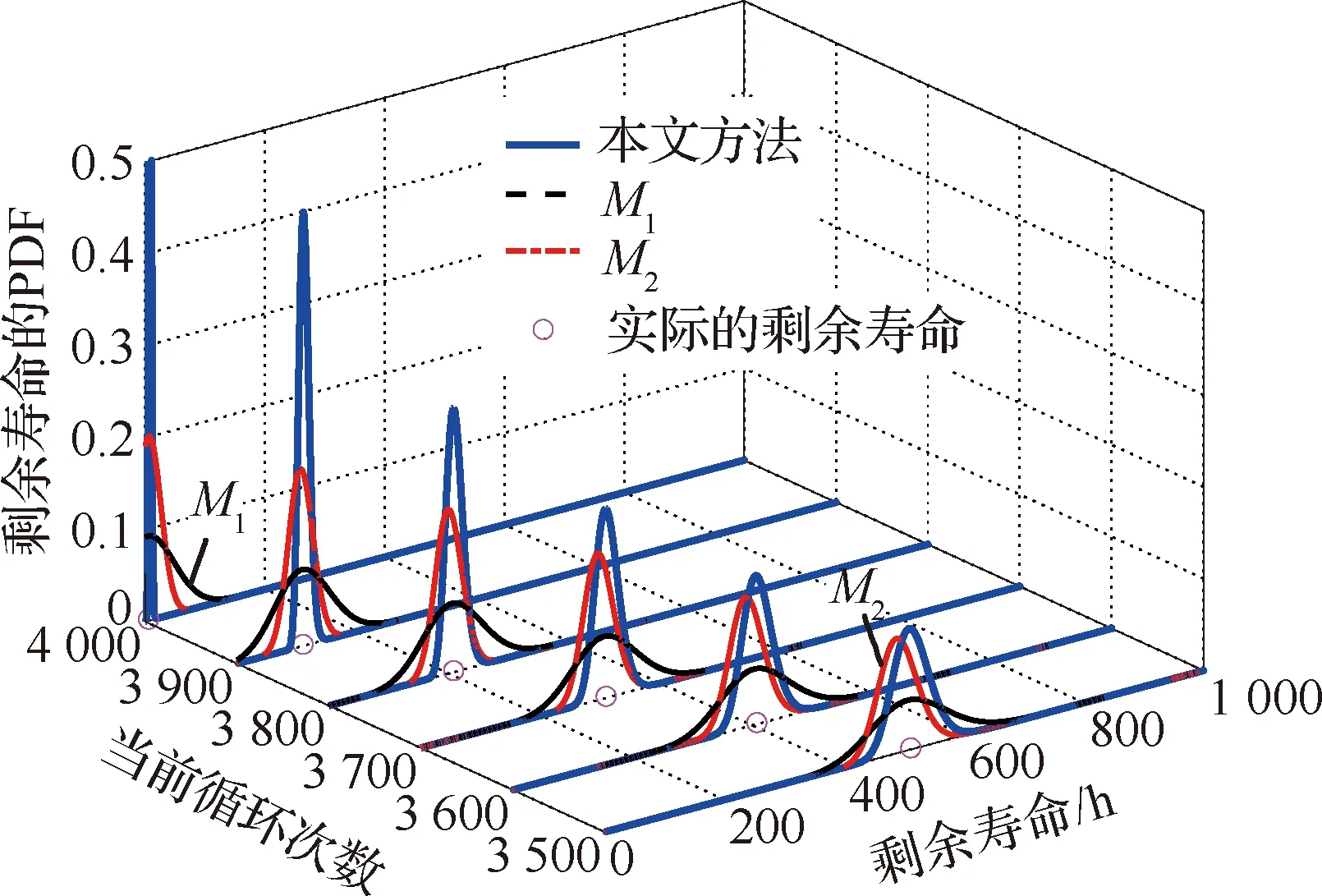
在以上框架下,本文的主要目標(biāo)是針對缺乏歷史數(shù)據(jù)和先驗信息的新研發(fā)航空發(fā)動機,利用實時監(jiān)測的性能衰減數(shù)據(jù)來自適應(yīng)地預(yù)測航空發(fā)動機的剩余壽命,并且在獲得新的性能衰減數(shù)據(jù)后實現(xiàn)對剩余壽命的在線更新。具體地,首先假定獲得的性能衰減數(shù)據(jù)是在離散時間點0=t0 (3) 考慮到表征設(shè)備健康水平的潛在性能衰減狀態(tài){X(t),t≥0}一旦首次達(dá)到設(shè)定的失效閾值ω(一般由工業(yè)標(biāo)準(zhǔn)設(shè)定)時,則認(rèn)為設(shè)備失效。因此,基于首達(dá)時間的概念[1-5],設(shè)備在tn時刻的剩余壽命Ln定義為 Ln=inf{ln>0:X(ln+tn)≥ω} (4) 相應(yīng)地,剩余壽命Ln的概率密度函數(shù)(PDF)為fLn|Y0:n(ln|Y0:n)。因此,預(yù)測航空發(fā)動機剩余壽命的關(guān)鍵是基于監(jiān)測的性能衰減數(shù)據(jù)Y0:n={y0,y1,…,yn},求解fLn|Y0:n(ln|Y0:n),并在獲得新的性能衰減數(shù)據(jù)后,實現(xiàn)剩余壽命分布的在線更新。 為了實現(xiàn)剩余壽命的自適應(yīng)預(yù)測,首先將式(3)進一步改寫為 (5) (6) 式中:δn~N(0,φn),且有 定義基于監(jiān)測數(shù)據(jù)Y0:n估計的zn的期望和協(xié)方差分別為 (7) 同樣地,定義一步前向的期望和協(xié)方差為 (8) 狀態(tài)估計 (9) 協(xié)方差更新 Pn|n=Pn|n-1-KnCPn|n-1 (10) 濾波初值 (11) 根據(jù)建立的狀態(tài)空間模型式(6),基于監(jiān)測的性能衰減數(shù)據(jù)Y0:n,計算剩余壽命的PDF為 fLn|Y0:n(ln|Y0:n)? (12) (13) 根據(jù)極大似然估計(MLE)理論,性能衰減數(shù)據(jù)Y0:n關(guān)于模型參數(shù)向量Θ的對數(shù)似然函數(shù)為 (14) (15) 然而,由于將潛在性能衰減狀態(tài)xn和隨機參數(shù)λn視作“隱含”狀態(tài),因此無法直接最大化式(15)。為解決這一問題,自然會采用期望最大化(EM)算法進行參數(shù)估計,通過最大化聯(lián)合似然函數(shù)p(zn,Y0:n|Θ)去逼近模型參數(shù)的MLE。EM算法的估計過程可以分為以下2步。 E步: (16) M步: (17) 首先,為了計算對數(shù)聯(lián)合似然函數(shù),可以通過條件概率公式得到 2lnp(zn,Y0:n|Θ)= 2[lnp(Y0:n|zn,Θ)+lnp(zn|Θ)]= (18) 然后,通過E步對式(18)求條件期望,有 (19) 式中: (20) 顯然,為了推導(dǎo)出E步結(jié)果,需要先計算式(20)。這里,本文采用Rauch-Tung-Striebel(RTS)平滑濾波算法[19]計算Ω、Ξ、Φ: 平滑濾波 (21) 協(xié)方差初值 Mn|n=(I2×2-KnC)AnPn-1|n-1 (22) 后向迭代 (23) 式中:Mi|n=cov(zi,zi-1|Y0:n)。基于RTS算法,條件期望Ω、Ξ、Φ可以計算為 (24) (25) (26) (27) (28) CM2:為了基于性能衰減數(shù)據(jù)Y0:n估計參數(shù)θ,首先將式(25)和式(28)一起代入到式(19)中,便可以通過最大化來估計參數(shù)即 (29) 由此可見,與傳統(tǒng)的EM算法相比,本文的ECM算法通過CM1和CM2兩步,可以將原本需要優(yōu)化的3個參數(shù)簡化為一個參數(shù)θ,降低了計算復(fù)雜度,提高了在線性能。此外,本文提出的參數(shù)估計方法可以在監(jiān)測到一個新的性能衰減數(shù)據(jù)時,實現(xiàn)對模型參數(shù)的自適應(yīng)估計和在線更新,克服了新研發(fā)航空發(fā)動機歷史數(shù)據(jù)和先驗信息不足的限制,這對于工程實際具有重要意義。 根據(jù)相關(guān)文獻可知,航空發(fā)動機的性能衰減和故障通常表現(xiàn)在排氣溫度裕度(EGTM)的衰減[22-23]。因此,EGTM是表征航空發(fā)動機健康狀態(tài)的一個重要指標(biāo)。EGTM的定義為航空發(fā)動機出廠前測定的排氣溫度(EGT)限制值與全推力(或全功率)起飛時實際的EGT之間的差值。隨著航空發(fā)動機工作時間的增加,EGT會逐漸升高,反映到EGTM就會逐漸衰退,因此準(zhǔn)確預(yù)測EGTM對提高航空發(fā)動機的可靠性至關(guān)重要。 實際中,由于外部環(huán)境和內(nèi)部因素的隨機性,航空發(fā)動機在某一時刻的性能衰減量也是隨機的,而且同類型航空發(fā)動機EGTM的衰減軌跡雖然具有相似性,但實際上不同個體之間仍然存在著差異性。因此,監(jiān)測的EGTM數(shù)據(jù)不僅會受到時變不確定性的影響,還會受到個體差異不確定性的影響。此外,EGT數(shù)據(jù)來源于航空發(fā)動機上安裝的傳感器,經(jīng)過空地數(shù)據(jù)鏈、報文解析程序等步驟進入到性能監(jiān)測系統(tǒng),在這整個過程中不可避免地會引入測量誤差,造成測量的不確定性。根據(jù)EGTM的定義可知,EGTM是基于EGT計算的,因此EGTM數(shù)據(jù)中必然存在測量誤差。通過上述分析發(fā)現(xiàn),監(jiān)測的EGTM數(shù)據(jù)中存在著三源不確定性共存的現(xiàn)象,因此同時考慮三源不確定性是必要的,也是更加符合實際需求的。下面以某型號航空發(fā)動機在6年內(nèi)監(jiān)測的EGTM數(shù)據(jù)來驗證本文方法的有效性,收集的性能衰減數(shù)據(jù)如圖1所示。根據(jù)工程經(jīng)驗,設(shè)定EGTM的失效閾值ω=0 ℃,并且考慮以下冪函數(shù)形式的性能衰減模型: 圖1 航空發(fā)動機的性能衰減路徑 X(t)=x0+λ·tθ+σBB(t) (30) 這里,根據(jù)EGTM數(shù)據(jù)的特點,選擇式(1)中非線性函數(shù)的形式為ρ(t;θ)=θ·tθ-1。到目前為止,此類模型已經(jīng)在航空發(fā)動機、軸承、電池等復(fù)雜系統(tǒng)的性能衰減建模中得到了廣泛的應(yīng)用[3,12,17]。 如圖1所示,監(jiān)測間隔為100次循環(huán),在監(jiān)測到第4 000次循環(huán)時,EGTM首次達(dá)到失效閾值ω,期間共監(jiān)測了41次。顯然,隨著循環(huán)次數(shù)的增加,航空發(fā)動機的性能衰減路徑整體呈下降趨勢。然而,本文所提出的剩余壽命預(yù)測方法是基于性能衰減路徑呈上升趨勢的情況下推導(dǎo)出來的,因此需要對原始性能衰減數(shù)據(jù)進行轉(zhuǎn)換。這里,本文利用EGTM的初始值減去其他所有的性能衰減數(shù)據(jù),相應(yīng)地,失效閾值轉(zhuǎn)換為初始值減去ω。下面,基于轉(zhuǎn)換后的性能衰減數(shù)據(jù)來驗證本文方法的有效性和優(yōu)越性。隨著性能衰減數(shù)據(jù)的積累,采用所提出的參數(shù)估計方法可以對模型參數(shù)Θ在每一個監(jiān)測點進行自適應(yīng)地估計和更新,結(jié)果如圖2所示。 圖2 模型參數(shù)的自適應(yīng)估計過程 圖2的結(jié)果表明,模型參數(shù)可以隨著性能衰減數(shù)據(jù)的積累很快地收斂,并且在獲得一個新的性能衰減數(shù)據(jù)時,模型參數(shù)和剩余壽命的PDF都可以進行自適應(yīng)地估計和更新。因此,克服了歷史數(shù)據(jù)和先驗信息不足的限制,能夠適用于新研發(fā)航空發(fā)動機的剩余壽命預(yù)測。 為了進一步證明本文方法的優(yōu)越性,選擇以下2種方法進行對比研究: 圖3給出了3種方法在最后6個監(jiān)測點預(yù)測的剩余壽命的PDF曲線,從圖中可以看出,3種方法得到的PDF曲線均包含了實際的剩余壽命,且隨著循環(huán)次數(shù)的增加逐漸變窄,這意味著預(yù)測的剩余壽命的不確定性越來越低。此外,由于本文方法在性能衰減建模中同時考慮了三源不確定性,并且在每一個監(jiān)測點可以對模型參數(shù)進行自適應(yīng)地估計和在線更新,因此本文方法得到的PDF曲線更加窄而尖銳,說明本文方法在剩余壽命預(yù)測方面具有更高的精度和更好的性能。 圖3 三種方法的比較結(jié)果 為了進一步量化比較結(jié)果,本文采用可靠性領(lǐng)域中常用的均方誤差(MSE)指標(biāo),該指標(biāo)同時考慮了剩余壽命預(yù)測的精度和不確定性,在tn時刻的定義式為 (31) 圖4 所有監(jiān)測點的MSE 圖5 4個不同監(jiān)測點的箱形圖(點劃線表示實際剩余壽命) 圖4給出了3種方法在所有監(jiān)測點的MSE比較結(jié)果。由于本文方法和M2方法均不依賴于歷史數(shù)據(jù)和先驗信息,且模型的初始參數(shù)是隨機給定的,因此在監(jiān)測初期性能衰減數(shù)據(jù)較少時,剩余壽命預(yù)測的MSE高于M1,但隨著性能衰減數(shù)據(jù)的積累,本文方法的MSE明顯低于M1和M2。為進一步驗證,圖5給出了4個不同監(jiān)測點的箱形圖。其中,箱子的大小表示預(yù)測的剩余壽命的不確定性,若箱子越大,則預(yù)測的不確定性越大,精度越低;點劃線表示當(dāng)前監(jiān)測點的實際剩余壽命;箱子中的實線表示預(yù)測的剩余壽命的期望,實線越接近點劃線,說明預(yù)測的精度越高,結(jié)果越準(zhǔn)確。從圖5(a)中可以看出,此時由于性能衰減數(shù)據(jù)較少,M1優(yōu)于本文方法和M2,但是隨著性能衰減數(shù)據(jù)的積累,本文方法的箱子更小且更加接近實際的剩余壽命,如圖5(b)~圖5(d)所示。此外,引入相對誤差(RE)指標(biāo)來進一步量化剩余壽命預(yù)測的精度,在壽命的20%、45%、70%和95%分位點上分別給出了3種方法RE的比較結(jié)果,如表1所示。 通過表1的結(jié)果可以看出,本文方法可以有效減少剩余壽命預(yù)測的RE,進而提高了剩余壽命預(yù)測的精度,尤其在壽命的95%分位點處,剩余壽命預(yù)測的RE僅為1.68%,明顯小于其他2種方法。以上的實驗結(jié)果表明,本文方法具有更好的預(yù)測能力,剩余壽命預(yù)測的精度更高,且不依賴于歷史數(shù)據(jù)和先驗信息,更加適用于新研發(fā)的航空發(fā)動機。 表1 不同壽命分位點相對誤差的比較結(jié)果 1) 本文在三源不確定性下建立了非線性的性能衰減模型,不僅克服了現(xiàn)有方法的潛在假設(shè),而且可以較好地建模航空發(fā)動機的性能衰減軌跡,并能夠?qū)⑷床淮_定性的影響納入到預(yù)測的剩余壽命分布中。 2) 利用Kalman濾波技術(shù)可以對潛在的性能衰減狀態(tài)進行實時估計,并基于首達(dá)時間的概念,得到了同時考慮三源不確定性的剩余壽命分布。 3) 在獲得一個新的性能衰減數(shù)據(jù)時,基于RTS平滑和ECM算法對模型參數(shù)進行自適應(yīng)地估計和在線更新,克服了新研發(fā)航空發(fā)動機缺乏歷史數(shù)據(jù)和先驗信息的問題,降低了參數(shù)估計的不確定性,顯著提高了剩余壽命預(yù)測的精度,尤其在壽命的95%分位點處,剩余壽命預(yù)測的RE僅為1.68%。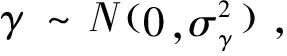

2 剩余壽命自適應(yīng)預(yù)測






3 基于ECM算法的模型參數(shù)估計















4 實例驗證








5 結(jié) 論

