基于隨機算法的抗混響目標探測方法

劉冰， 殷敬偉， 朱廣平， 郭龍祥

(1.哈爾濱工程的大學 水聲技術重點實驗室，黑龍江 哈爾濱 150001；2. 海洋信息獲取與安全工業(yè)和信息化部重點實驗室(哈爾濱工程大學)，黑龍江 哈爾濱 150001；3.哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001)

水聲探測有主動探測和被動探測2種方式。 主動探測是指聲吶發(fā)射聲波，通過對回波信號的處理實現(xiàn)對目標的探測。被動探測是指聲吶不發(fā)射聲波，通過處理被探測目標的輻射噪聲實現(xiàn)對目標的探測。長期以來，被動探測以其探測距離遠、隱蔽性好的優(yōu)點得到了廣泛應用。然而，隨著隱身技術的發(fā)展，潛艇輻射噪聲正在以平均每年1 dB的速度逐年降低，這給被動探測帶來了十分嚴峻的挑戰(zhàn)[1]。鑒于被動探測的局限性，主動探測受到了足夠的重視，并得到了充分的發(fā)展。在一些對隱蔽性沒有要求的場景下，例如海港監(jiān)測，主動探測往往能勝任更加復雜的探測任務[2-3]。然而，在主動探測中，混響的干擾是無法回避的。在某些情況下，目標回波會常常被淹沒在混響之中。而且，混響與發(fā)射信號有著強相干性，很難通過常規(guī)的方法抑制和消除。

對于如何降低混響給主動探測帶來的不良影響進而實現(xiàn)更好的探測性能，科研人員做了長期大量的研究。Kay等[4]提出了一種使用自回歸預白化的方法來抑制混響。該方法的核心思想是使用少量混響數(shù)據(jù)來構建一個自回歸濾波器，通過濾波來抑制混響。此后，高階統(tǒng)計算法[5]、歸一化最小均方算法[6]和變步長算法[7]相繼被提出用于改進預白化方法。這類方法的基本假設是混響恒定不變。在大多情況下，這種假設條件并不能嚴格滿足。因此，在混響較為復雜的環(huán)境下，其混響抑制能力十分有限。如果發(fā)射信號是線性調(diào)頻(LFM)信號，那么混響可以通過時頻域的處理進行抑制。Wigner-Ville分布(WVD)是一種優(yōu)秀的時頻轉(zhuǎn)換方法。水鵬朗等[8]利用交叉平滑偽WVD對相鄰的2個接收信號進行處理，并利用兩個結(jié)果的特征檢測目標。夏云龍等[9]在WVD之前增加了時間反轉(zhuǎn)鏡的處理實現(xiàn)了對多重散射的抑制。盡管在數(shù)值仿真中WVD能良好表示信號的能量分布，但在實際應用中交叉項的影響仍然限制了該類方法的性能。于歌等[10]利用分數(shù)傅里葉變換(FrFT)對LFM信號進行了能量聚焦，達到了抑制混響提高探測性能的效果，但這種方法的缺點是FrFT變換的階次很難選擇。

本文提出了一種基于隨機算法的抗混響探測方法，著眼于對各幀信號之間關聯(lián)特性的分析。不同于傳統(tǒng)的探測方法對一幀數(shù)據(jù)的處理，本文方法是將累積的多幀數(shù)據(jù)進行聯(lián)合處理。采用了低秩結(jié)構提取的計算抑制了混響，并在計算過程中對數(shù)據(jù)矩陣進行了非負約束，最終以迭代的形式實現(xiàn)了在強混響的環(huán)境下對移動目標的探測。本文方法能在低信混比的條件下探測到目標。

1 抗混響目標探測方法

1.1 低秩結(jié)構提取

低秩矩陣近似在數(shù)據(jù)分析和科學計算中扮演著一個重要的角色，截斷奇異值分解(truncated singular value decomposition)、秩呈現(xiàn)QR分解(rank-revealing QR decomposition)都可以作是低秩矩陣近似的一種形式。隨機算法為低秩矩陣近似提供了一個強有力的工具。在很多情況下，隨機算法比矩陣正交分解的算法，在精確程度、計算速度和魯棒性上有著明顯的優(yōu)勢。

考慮一個矩陣X∈RM×N，其潛在的低秩結(jié)構的秩為r。對其進行線性測量，即

(1)

來提取[12]。式中(·)?表示矩陣的廣義逆。為了提高低秩結(jié)構提取的精度，可以采用雙向投影的方式進行改進[13]。先進行行投影，即：

Y1=ΩX

(2)

然后以Y1為感知矩陣進行列投影，即：

Y2=Y1XT=ΩXXT

(3)

最后用Y2為感知矩陣替換Ω對X重新進行行投影，即：

Y3=Y2X=ΩXXTX

(4)

結(jié)合式(1)～(4)，則改進后的低秩結(jié)構提取公式為：

(5)

1.2 探測方法

本文方法的應用背景為在淺海對近距離的移動目標進行探測。首先做2點假設：1)聲線沿直線傳播；2)在時間上，前后幀混響具有較強的相關性。實際環(huán)境中，這2點假設十分容易滿足。淺海可以認為是一個等聲速梯度的環(huán)境，因而聲線不會發(fā)生彎曲。而且由于距離較近，聲信號非幾何衰減可以忽略，幾何衰減可以用自動增益控制進行補償。混響主要有海面散射、海水體積散射、海底界面散射三種來源。在淺海中，由于海底散射產(chǎn)生的混響占接收到混響中的主要部分。海底結(jié)構一般十分穩(wěn)定，因此聲吶接收到的各幀混響雖然不會完全相同，但會具有很強的相關性。

考慮一個主動聲吶重復發(fā)射一個脈沖信號N次，將第n個和第n+1個脈沖信號之間的接收信號進行波束形成，得到B[n]∈RNr×Nθ。其中，Nr是矩陣在距離方向上的維度，Nθ矩陣在角度方向上的維度。定義xn∈RNrNθ×1為B[n]的向量化，即：

xn=[b1[n];b2[n];…;bj[n];…;bNθ[n]]

式中，bj[n]為B[n]的第j列。則多幀接收的數(shù)據(jù)可以用一個NrNθ×N的矩陣來表示，即

X=[x1,x2,…,xn,…,xN]

前文中提到，混響具有強相關性，則多幀數(shù)據(jù)矩陣X的各列具有強相關性，因此X必定具有潛在的低秩結(jié)構。之所以稱X具有低秩結(jié)構而不是直接稱X為低秩矩陣，是因為X各列中存在非相關的分量。這些非相關的分量對X的影響是少量的、局部的，因此X可以被分解為一個低秩矩陣和一個稀疏矩陣加和的形式，即：

X=L+S

(6)

式中：L∈RNrNθ×N表示低秩部分，其包含了混響的相關部分，S∈RNrNθ×N表示稀疏部分，其包含了運動目標、混響的非相關部分和噪聲。一般情況下，運動目標的能量要大于混響的非相關部分和噪聲，S∈RNrNθ×N可以進一步拆分為S′∈RNrNθ×N和Z∈RNrNθ×N兩部分。S′包含了運動目標，Z包含了混響的非相關部分和噪聲，可以用一個閾值ξ來區(qū)分二者，即：

S′=Thξ[S]

Z=S-S′

式中：Thξ[·]為閾值函數(shù)，若Si,j、S′i,j分別為S、S′第i行、第j列的元素，則

于是式(6)可以寫成：

X=L+S′+Z

將得到的S′進行逆向量化可以得到每一幀數(shù)據(jù)的探測結(jié)果D[n]∈RNr×Nθ。整個數(shù)據(jù)處理流程如圖1所示。

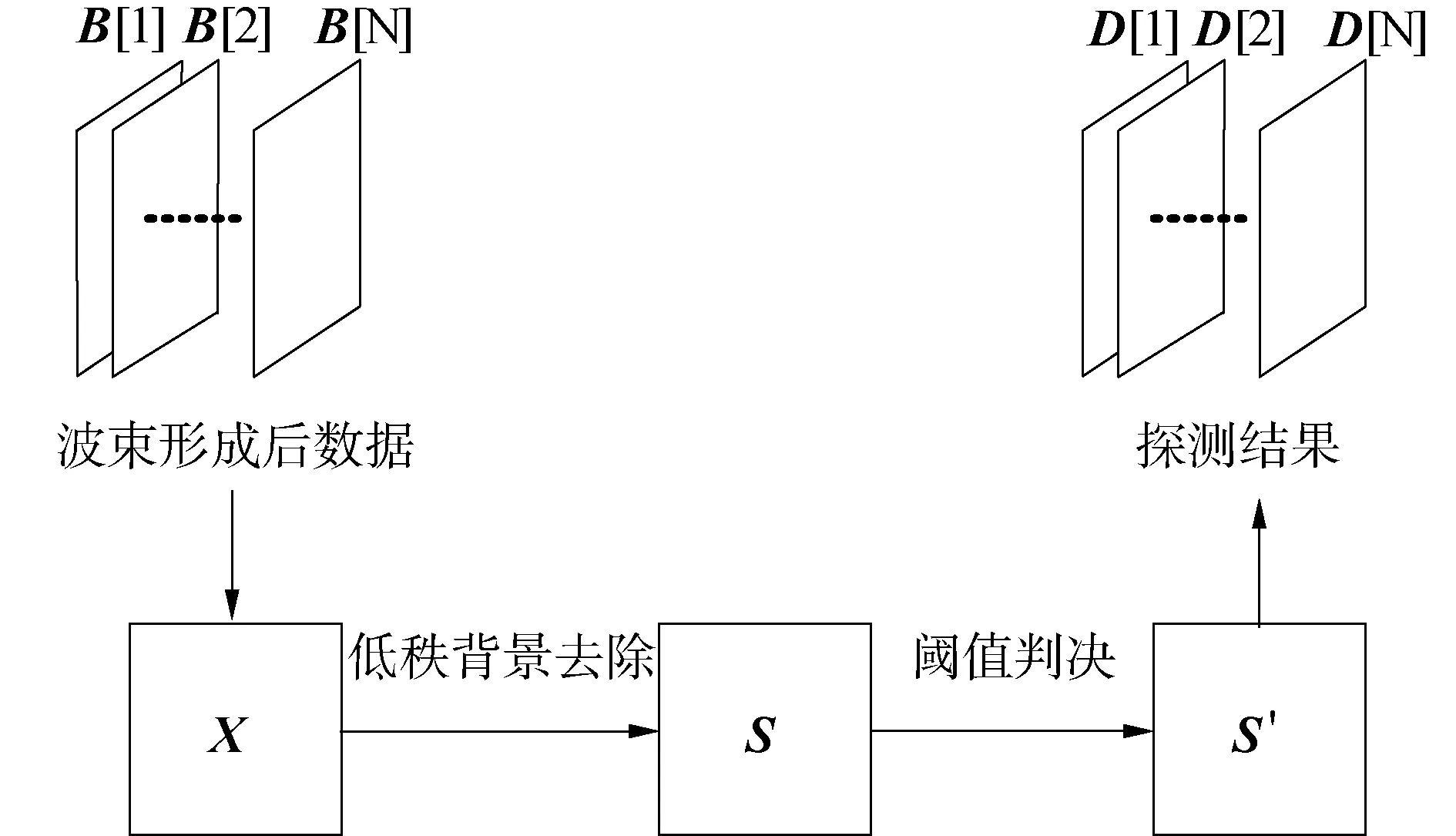
圖1 數(shù)據(jù)處理流程Fig.1 Processing flow of the beamforming data

上述過程的關鍵在于如何求得L并從X。雖然1.1節(jié)中介紹了如何提取矩陣的低秩結(jié)構，但是對于低秩結(jié)構非常明顯的矩陣，很難將低秩部分和稀疏部分進行分離。為了解決這一問題，本文加入了對矩陣的非負約束，并使用迭代方法。因為處理的數(shù)據(jù)為波束形成后的數(shù)據(jù)，所以分解后的矩陣都應該是非負矩陣。加入非負約束是迭代的前提，通過迭代可以使低秩結(jié)構提取逐步精確。目標探測方法步驟總結(jié)如下：

1)設置輸入?yún)?shù)。數(shù)據(jù)序列{B[n]}，最大迭代次數(shù)K，門限ξ，相對誤差上限ε；

2)初始化。令S=0，生成感知矩陣Ω，向量化{B[n]}→X,X=XT；

3)迭代。

fork=1:K∥K次迭代

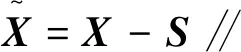
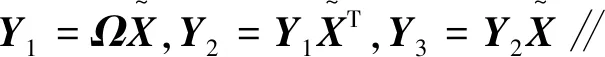
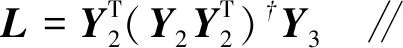
S=X-L∥ 計算數(shù)據(jù)矩陣稀疏部分

S=Th0[S]∥ 非負約束

If ‖X-S-L‖F(xiàn)/‖X‖F(xiàn)<ε, break; end

∥ 判斷是否終止迭代，‖·‖F(xiàn)為Frobenius范數(shù)

end

4)閾值檢測。S′=Thξ[S]；

5)逆向量化并輸出探測結(jié)果。S′=S′T,S′→{D[n]}。

值得注意的是，數(shù)據(jù)矩陣X中的低秩結(jié)構來源于混響，而各幀混響具有強相關性，則X的低秩部分秩應該為1，即r=1。另外，聲吶數(shù)據(jù)的數(shù)據(jù)量一般不會很大，因此NrNθ?N，因此，在計算中，算法開始之前對X進行轉(zhuǎn)置處理，并在對S′逆向量化之前進行轉(zhuǎn)置處理，有助于減小計算量。

2 數(shù)值仿真與實驗

為了討論在不同情況下本文目標探測方法的性能，接下來將進行一系列的數(shù)值仿真。在對檢測算法進行數(shù)值仿真之前首先需要建立一個混響模型。定義R[n]∈RNr×Nθ為波束空間中的第n幀混響序列，則各幀混響可以由下式得到

R[n]=βR[0]+(1-β)A[n]

(7)

式中：β是一個用來控制混響相關和非相關部分比例的參數(shù)；R[0]表示初始能量分布，它由實際水域中散射體的分布和性質(zhì)決定；A[0]表示第n幀混響的非相關部分。若Ai,j[n]表示A[n]的第i行、第j列的元素，則：

Ai,j[n]=αAi,j[n-1]+(1-α)v

(8)

式中：0<α<1是一個隨機變量，控制著混響非相關部分變化的劇烈程度。

使用上述混響模型生成20幀混響。參數(shù)設置為Nr=200,Nθ=60,α=0.8,β=0.8，Ai,j[0]=0；R[0]是一個服從二維瑞利分布的隨機矩陣，其尺度參數(shù)設置為1，v是一個服從高斯分布的隨機變量，其期望為0，方差為1。在生成的混響數(shù)據(jù)中添加一個移動目標，目標強度為0.5，用矩陣T[n]∈RNr×Nθ來表示第n幀混響中添加的目標。若Ti,j[n]表示矩陣T[n]的第i行、第j列的元素，則

使用此數(shù)據(jù)進行一次抗混響目標探測實驗，實驗結(jié)果如圖2所示。圖2(a)原始數(shù)據(jù)的某一幀由于強混響的存在，目標被掩埋在混響之中，幾乎不能被分辨出來。圖2(b)是經(jīng)過低秩提取后各幀中非相關部分，其中包括運動目標和混響中時變的部分。從圖中可以看出，原本在圖2(a)中隱藏的目標顯現(xiàn)出來了，但是結(jié)果中還殘留了一部分干擾。圖2(c)是經(jīng)過閾值判決得到的目標探測結(jié)果。由于殘留的干擾較弱，經(jīng)過閾值判決后，殘留干擾被完全消除了。將各幀目標探測的結(jié)果進行疊加，于是得到了目標的運動軌跡，如圖2(d)所示。數(shù)值仿真結(jié)果表明，本文所提出的抗混響探測方法在理論上是可行的。

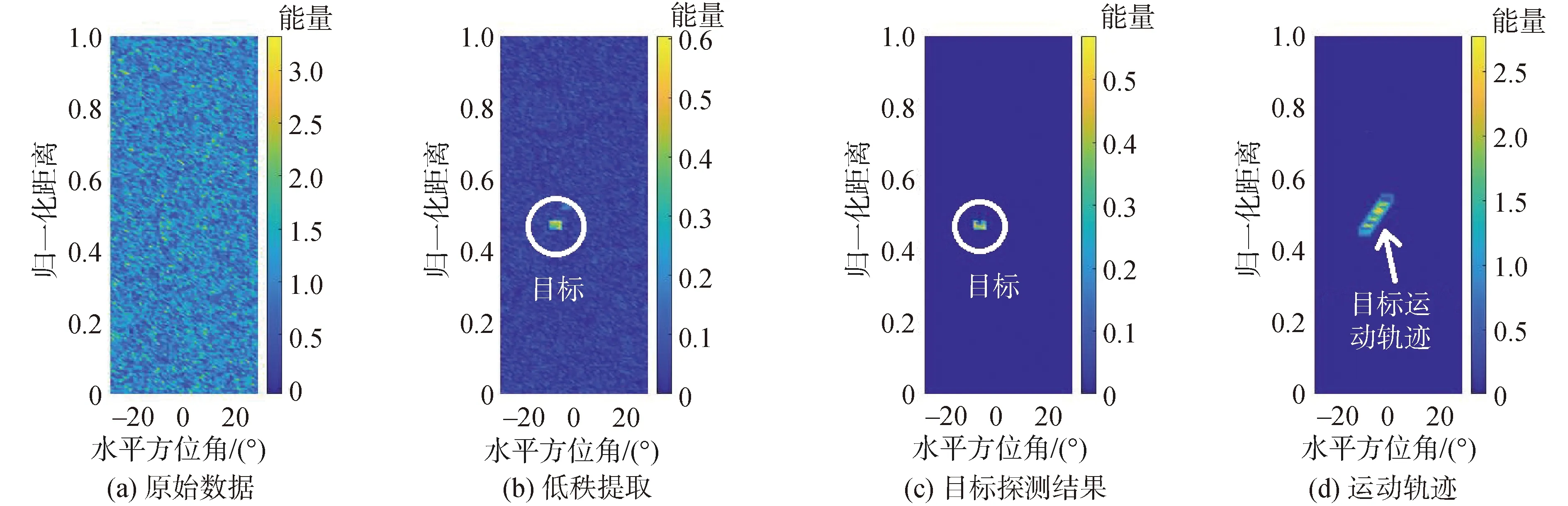
圖2 抗混響目標探測仿真結(jié)果Fig.2 Simulation results of target detection with reverberation suppression

為了定性分析本文方法在不同混響環(huán)境下的效果，下文將進行進一步討論。定義各幀的探測誤差為：

E[n]=‖T[n]-D[n]‖F(xiàn)

本文用探測誤差來衡量探測能力。探測誤差越小，說明探測方法的能力越強。

圖3 抗混響目標探測探測誤差Fig.3 Detection error of target detection with reverberation suppression

調(diào)整混響模型參數(shù)α和β，其他參數(shù)保持和之前數(shù)值仿真一致，得到數(shù)值仿真結(jié)果如圖3所示。圖3(a)為保持β=0.8不變，α分別取值為0.2、0.4、0.6、0.8和1時的探測誤差。圖3(b)為保持α=0.8不變，β分別取值為0.2、0.4、0.6、0.8和1時的探測誤差。從圖3中可以看出，在α和β相同的情況下各幀的探測誤差有所波動但基本維持在同一水平上；而保持α和β其中之一不變，逐步增大另一個參數(shù)時，探測誤差逐漸變小。由式(7)和(8)可知，α和β共同決定著各幀混響之間的相關性，α和β越大，各幀混響之間的相關性就越強。因此可以得出結(jié)論，混響的相關性越強，本文探測方法的性能就越好。

為了驗證算法的實際探測能力，在黑龍江省哈爾濱市松花江進行了外場實驗。操作一個遙控無人潛水器(ROV)作為此次實驗待探測的目標，使用前視聲吶對其進行探測。此次實驗收集到25幀數(shù)據(jù)，每幀數(shù)據(jù)波束形成后得到一個230×60的矩陣，其中在距離方向上有230個采樣點，在角度方向上有60個采樣點。數(shù)據(jù)處理過程中對距離和能量都進行了歸一化。實驗數(shù)據(jù)處理結(jié)果如圖4所示。

圖4(a)原始數(shù)據(jù)的某一幀，由于強混響干擾的存在，目標的具體位置很難被分辨出。圖4(b)是經(jīng)過低秩提取后各幀中非相關部分，其中包括運動目標和混響中時變的部分。從中可以看出，大部分混響已經(jīng)被移除，運動目標開始顯露出來，但是由于殘留的混響干擾范圍較大，目標在圖中并非十分明顯。圖4(c)是經(jīng)過閾值判決得到的目標探測結(jié)果。殘留混響雖然影響面積很大，但是能量并不是很強，通過閾值判決后，圖4(c)中目標依然被清晰地探測出來。圖4(d)是將各幀目標探測的結(jié)果進行疊加得到的目標的運動軌跡。該結(jié)果與數(shù)值仿真結(jié)果類似，都十分清晰。實驗結(jié)果表明，本文方法在真實環(huán)境中也是有效的。

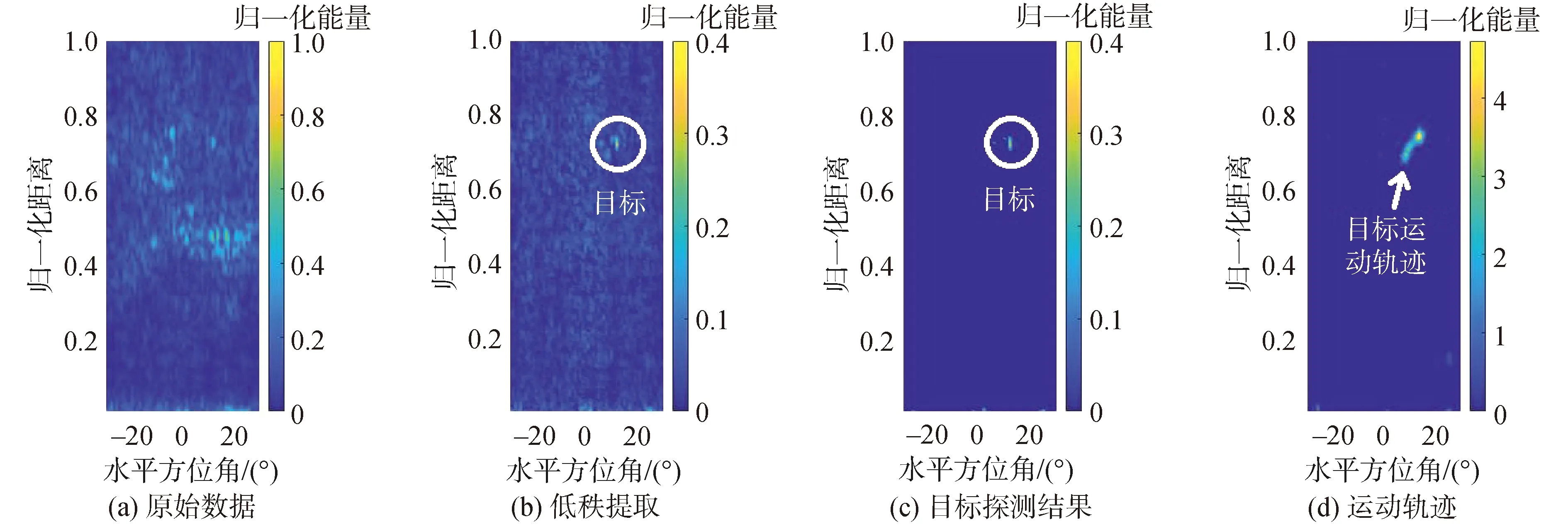
圖4 抗混響目標探測實驗結(jié)果Fig.4 Experiment results of target detection with reverberation suppression

3 結(jié)論

1) 隨機算法作為一種高效的算法，能夠?qū)仃嚨牡椭炔糠诌M行的提取。

2) 本文對多幀接收數(shù)據(jù)組成的矩陣進行了低秩結(jié)構提取，并在處理過程中加入了非負約束條件，最終以迭代的方式成功實現(xiàn)了混響和目標的分離。本文提出的方法在理論上是可行的。

3) 本文所提出的方法在不同條件下，性能有所差異。數(shù)值仿真表明，各幀混響的相關性越強，目標探測效果就越好。

4) 本文所提出的方法在實際中也具有良好的探測性能，具有良好的推廣前景。