基于馬爾科夫GM(1,1)模型的物流貨運量預測研究與應用
馬睿
[摘要]物流貨運量是衡量物流行業發展快慢的重要指標。針對不確定影響因素較多的物流貨運量預測采用傳統GM(1,1)模型預測,預測結果精準度較低。針對該問題,提出了基于馬爾科夫原理的GM(1,1)模型,進行物流貨運量預測研究與分析應用。根據馬爾科夫GM(1,1)模型原理,以近幾年的某地物流貨運量為研究數據,通過實際應用研究結果可知,該方法預測效果較好,為研究物流發展提供參考。
[關鍵詞]馬爾科夫鏈;GM(1,1)模型;物流貨運量
[DOI]1013939/jcnkizgsc202009169
1引言
隨著現代物流業的快速發展,物流貨運量也在不斷地增長。影響物流發展的重要因素是物流貨運量的增長速度,物流貨運量的多少決定了物流企業的經濟狀態。物流主要是通過鐵路、航空、水路和公路進行貨物周轉和運輸。在現代高速發展的國際物流和國內物流中,由于物流貨運量數據繁雜,對于貨運量統計存在著很大難度,也造成統計的數據缺乏精準度。[1]為了滿足日益增長的物流需求,推動物流行業的快速發展,建立合理的物流貨運量的預測模型是非常重要的。為了加快物流業的快速發展,在規劃物流體系的建設上實行改革創新,通過科學合理的馬爾科夫GM (1,1) 預測模型對物流貨運量進行預測,對物流系統的應用效果加以完善,使模型的預測準確值達到標準,同時要加強物流業的管理和建設,促進我國物流業的快速發展。[2]
2馬爾科夫GM(1,1)模型
21馬爾科夫GM(1,1)模型原理
馬爾科夫灰色模型預測原理是:①對最初特征數據進行處理,生成具有較強規律性的數據序列。②計算灰方程參數,建立相應的灰色微分方程。③建立GM(1,1)預測模型,由預測模型做第一次預測。④將馬爾科夫理論與預測模型結合,進一步對模型優化改進,通過利用馬爾科夫原理將數據劃分狀態,建立狀態轉移矩陣。⑤通過馬爾科夫原理獲取待預測年份所處狀態的邊界值,計算出預測年度的預測修正值,進而得到預測值。
由預測原理可知,該過程是隨機的,因此,馬爾科夫預測過程是一個隨機變動過程,事物每一次變動結果都是具有狀態轉移的無后效性。對馬爾科夫進行分析可知,該過程是由一種狀態隨機轉變為另一種狀態,即為轉移過程。根據該過程,能夠分析事物轉移狀態相關屬性,進而確定前狀態、后狀態和轉移狀態三者之間的關系,即為預測事物變動結果,依據此來預測物流貨運量未來幾年變動情況。
22模型應用——物流貨運量預測
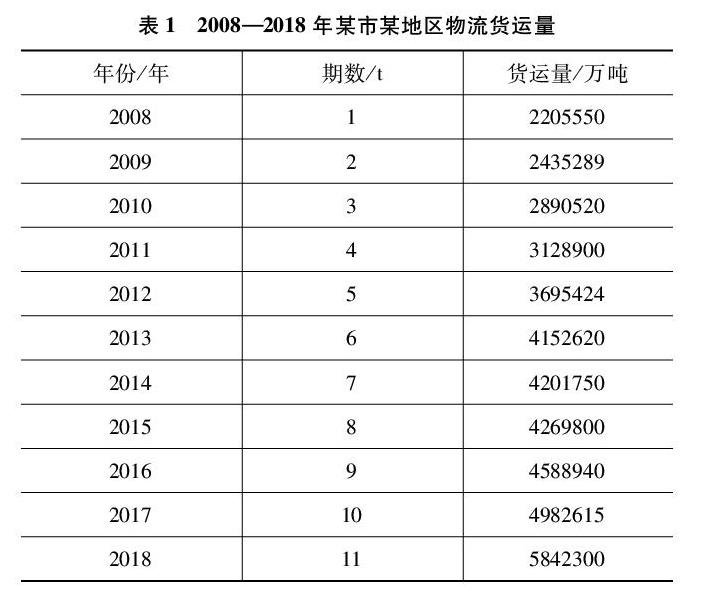
隨著物流業迅速發展,某地區實際貨運量也呈上升趨勢,對該地區實際貨運量進行量化處理,分析物流貨運量如表1所示。
由表1可看出,某地區實際物流貨運量出現了逐年遞增趨勢,在年份為2012、2013、2018時貨運量變化較大。該數據是由官方提供的真實性數據,結合某地區實際物流貨運量,預測方法具體實現步驟如下所示。
在預測前先把數據進行規劃處理,運用實際物流貨運量的數據進行預測實驗。計算灰色預測模型的灰數,得出灰色預測模型。用數學語言描述隨機過程,將時間集合,保證狀態空間是離散的,由此獲取時間狀態離散集,在規定時間內,統計離散集下的概率,利用馬爾科夫原理將數據劃分狀態,建立狀態轉移矩陣。當時間系統處于一個狀態時,每個狀態都具有n個轉向,由此計算該狀態下的概率,即系統在規定時間內系統處于狀態空間條件下的條件概率,集合一步轉移概率形成狀態概率矩陣。由一步轉移概率轉向為k步轉移概率,進而形成k步轉移概率矩陣。通過馬爾科夫原理得出預測年份所處狀態的邊界值,進而計算出預測年份的修正值,再計算出預測值。
3結果分析
針對研究的馬爾科夫GM(1,1)模型的物流貨運量預測方法有效性進行實驗驗證分析,以某市為研究對象預測,將傳統方法與所提方法的預測精準度進行對比分析。采用傳統預測方法準確度不高,始終低于80%,而采用馬爾科夫灰色預測法預測準確度較好,始終高于85%。傳統方法預測的準確度在2015年時達到最高為80%,在2012年時是最低為74%;馬爾科夫灰色預測法預測準確度最高在2017年時為94%,最低在2013年為85%。
4結論
在現階段的物流企業系統運行中,物流貨運量在運輸、周轉等過程中作為基礎數據,通過應用馬爾科夫GM(1,1)模型預測能夠對物流貨運量進行合理性分析,進而提高預測結果精準度。物流企業在實際應用中,可以根據企業的實際情況進行修改和完善,建立更精確的預測模式,確保預測值的準確性,滿足物流企業需求。采用合理預測能夠幫助企業穩定經營,這是保障物流行業穩定發展的前提,也是物流企業運營的關鍵。雖然采用馬爾科夫GM(1,1)預測,能夠改變采用傳統方法預測精準度低的問題,但影響物流貨運量的因素還有很多,在文章研究模型中未做出假設。因此,在不同的環境下對物流貨運量進行預測還有進一步對模型改進的空間。
參考文獻:
[1]時冬青, 宋文華, 張桂釧,等 基于灰色GM(1,1)-馬爾科夫模型的職業病預測研究[J]. 中國安全生產科學技術, 2017, 13(4):176-180
[2]張志明 基于新陳代謝-GM(1,N)馬爾科夫的軌道交通客運量預測方法[J]. 公路交通科技, 2018, 35(12):145-154
[3]趙振武, 麻建軍 基于灰色馬爾科夫模型的機場安檢危險品數量預測[J]. 安全與環境學報, 2017, 17(1):51-53
[4]紀伊琳, 錢政 基于殘差補償灰色馬爾科夫模型的校準間隔預測方法[J]. 電測與儀表, 2017, 54(21):13-17
[5]嚴雪晴 基于灰色模型的廣東高技能物流人才供需預測研究[J]. 數學的實踐與認識, 2017, 47(17):313-320

