直驅風電機組與SVG交互作用引發次/超同步振蕩的機理與特性研究

曹 娜，管雪帥，于 群，李 琰

（1.山東科技大學 電氣與自動化工程學院，山東 青島 266590；2.中國電力科學研究院有限公司，北京100192）

0 引言

隨著以風電為代表的新能源發展，直驅風電機組 （direct drive permanent magnet synchronous generator，DPMSG）因其自身的優良特性，得到了較多的應用[1]，[2]。由于風電場中的風電機組變流器、無功補償裝置等電力電子裝置響應速度快、無慣性、過載能力弱、抗電網擾動能力差等限制，其控制能力對外部電網環境具有較強的依賴性[3]。因此，風電機組與無功補償裝置之間的運行控制相互耦合和影響，有可能誘發并加劇風電機組發生次/超同步振蕩的風險。

針對直驅風電場接入弱交流系統出現的次/超同步振蕩現象，文獻[4]基于小擾動的導納分析法，建立了直驅風機端口輸入導納模型。文獻[5]利用正、負序阻抗建模方法，研究直驅風電機組并網產生次同步振蕩的機理，并提出了一種鎖相環優化方法。文獻[6]在考慮鎖相環和解耦控制環節的基礎上，采用小信號方法，對直驅風機匯集母線存在的多個次/超同步頻率分量現象給出理論解釋。文獻[7]通過推導直驅風電機組網側變流器（grid side converter，GSC）控制環節與電網之間諧波的響應過程，分析了次/超同步振蕩的引發機理并給出了穩定性判據。上述研究多基于直驅風電并網對電力系統穩定性的影響，缺乏對無功補償裝置與直驅風電機組的運行控制相互耦合作用的認識。

本文根據直驅風電機組網側變流器與靜止無功發生器（static VAR generators，SVG）的電路拓撲及控制策略，利用諧波線性化方法，建立了直驅風電機組與SVG交互作用的正序阻抗模型，并給出了基于阻抗的穩定性判據。在此模型基礎上，利用波特圖分析SVG控制參數對直驅風電機組的影響，揭示鎖相環和電流環控制參數對直驅風電機組與靜止無功發生器交互作用的次/超同步振蕩特性的作用規律。最后，在Matlab/Simulink中搭建直驅風電機組并網系統模型進行時域仿真，并與頻域分析結果比較，驗證了阻抗特性分析的合理性。

1 直驅風電機組和SVG正序阻抗模型

風電場中包含n臺同型號的1.5 MW直驅風電機組，它們連接于同一條母線上，且控制參數與運行狀態一致。風電場發出的電能經升壓變壓器接入110 kV交流主網，場內安裝有無功補償裝置SVG。

利用對稱分量法并結合諧波線性化方法，將系統分解成正、負序兩個子系統，對于三相平衡的對稱系統而言，不存在負序分量。本文在平衡工況下建立直驅風電機組和SVG正序阻抗模型，主要考慮二者的電路結構、控制策略對阻抗特性的影響。

圖1為電網電壓定向控制的GSC基本電路及控制策略。圖中：Uwdc為直流側電壓；Lw為濾波電感；Cw為直流側電容；Cfw為濾波電容；Rfw為阻尼電阻；uwa，uwb，uwc為 GSC 輸出電壓；ua，ub，uc和iwa，iwb，iwc分別為GSC的公共并網點（point of common coupling，PCC）三相電壓和電流；Zg為電網電抗；uga，ugb，ugc為交流電網三相電壓；Hwi（s）為GSC的電流調節器傳遞函數；Gwi（s）為電流采樣延時環節等效傳遞函數；Kwdq為GSC的交叉解耦系數。

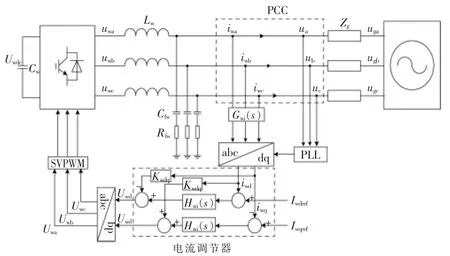
圖1 直驅風電機組網側變流器主電路拓撲Fig.1 The main circuit topology of grid-side converter in full-scale power converter turbine

圖2為SVG基本電路及控制策略。圖中：Usdc為直流側電壓；Ls為濾波電感；Cs為直流側電容；usa，usb，usc為 SVG 輸出電壓；ua，ub，uc和 isa，isb，isc分別為SVG的公共并網點三相電壓和電流；Hsi（s）為SVG的電流調節器傳遞函數；Gsi（s）為電流采樣延時環節等效傳遞函數；Ksdq為SVG的交叉解耦系數。

圖2 SVG主電路拓撲Fig.2 The main circuit topology of SVG

1.1 直驅風電機組和SVG鎖相環諧波線性化

直驅風電機組GSC和SVG采用同步靜止坐標系鎖相環 （synchronous reference frame phase locked loop，SRF-PLL），兩個鎖相環中的傳遞函數HwPLL（s）和 HsPLL（s）分別為

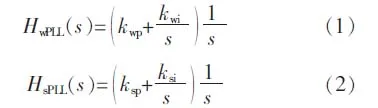
式中：kwp，kwi和 ksp，ksi分別為直驅風電機組 GSC和SVG的鎖相環比例系數與積分系數。

對直驅風電機組的PLL進行頻率特性分析。根據諧波線性化方法，假設特定頻率的正序電壓諧波分量存在于公共并網點，PLL通過對PCC電壓鎖相，得出dq軸坐標系坐標變換角度θ。假設 θ=θ1+Δθw，其中，θ1為正序基頻電壓產生的穩態同步并網相角，Δθw為正序電壓諧波產生的擾動相角，得到與 Δθw之間的傳遞函數為[8]

1.2 直驅風電機組與SVG正序阻抗模型

圖1中，直驅風電機組輸出電壓、電流和PCC處電壓之間的關系為

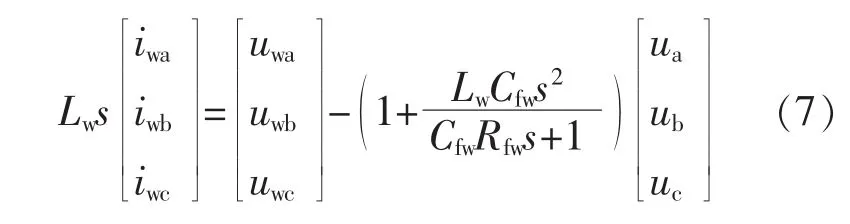
直驅風機并網電流經坐標變換和傅里葉變換得到其頻域表達。在通過電流調節器后，得到dq軸電壓指令值，然后分別經過以θ1和θ為旋轉角的帕克反變換轉換到abc坐標下，得到不考慮PLL和考慮PLL的直驅風電機組輸出電壓的頻域表達式。結合并網點電流和并網點電壓的頻域表達，并帶入式（7）中，可分別推得不含鎖相環和含鎖相環的直驅風機GSC正序阻抗模型為[8]

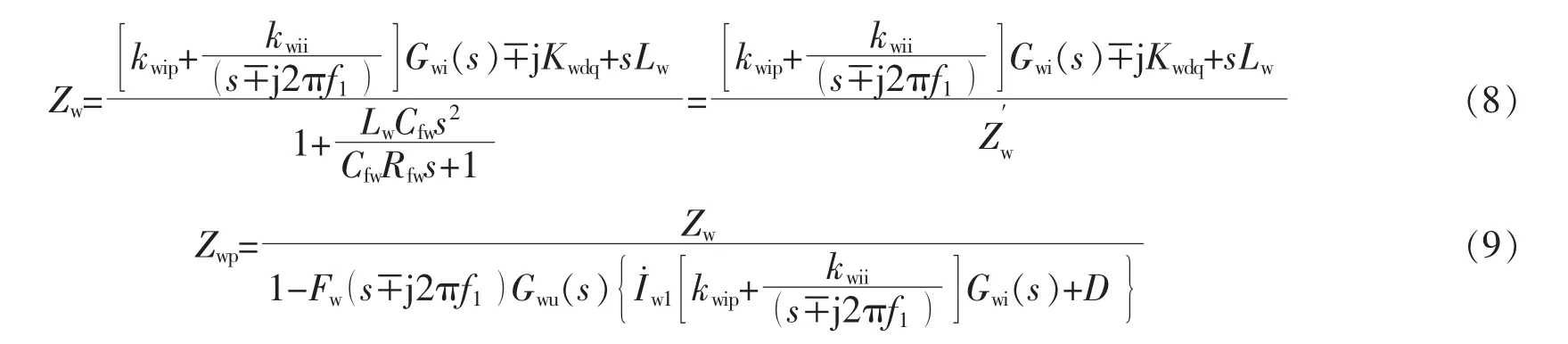
式中：kwip，kwii分別為直驅風電機組GSC電流調節器比例系數、積分系數；Kwdq為GSC的交叉解耦系數；Gwi（s）為電流采樣延時環節等效傳遞函數[5]；D=1/2Dw±j1/2Qw，其中 Dw，Qw分別為直驅風電機組電流調節器 d，q 軸的直流輸出量[8]；Gwu（s）為電壓采樣延時環節等效傳遞函數[5]；Iw1為基波電流幅值。

同理，根據圖2中SVG輸出電壓、補償電流和PCC處電壓關系，也可得到不考慮PLL和考慮PLL兩種情況的SVG阻抗模型，分別如式（10），（11）所示。

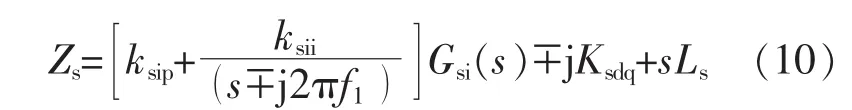
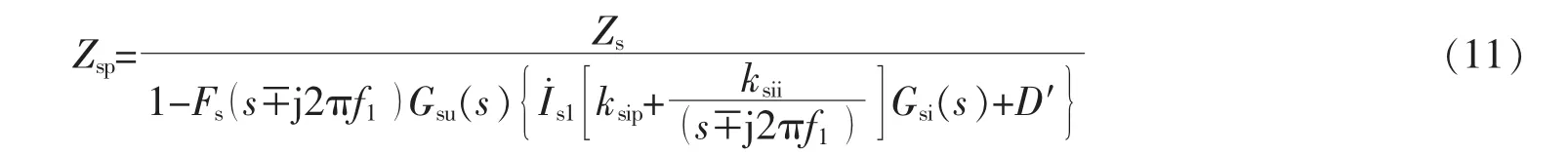
式中：ksip，ksii分別為SVG電流調節器比例系數、積分系數；Ksdq為 SVG 交叉解耦系數；Gsi（s）為電流采樣延時環節等效傳遞函數；D′=1/2Ds±j1/2Qs，其中Ds，Qs分別為 SVG電流調節器 d，q軸直流輸出量；Gsu（s）為電壓采樣延時環節等效傳遞函數。

2 直驅風電機組與SVG交互的正序阻抗模型

2.1 不考慮PLL的交互阻抗模型

不考慮鎖相環的影響，由式（8），（10）可得不含鎖相環的二者交互的正序阻抗模型為

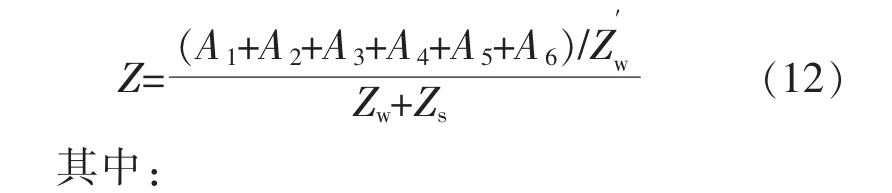
2.2 考慮PLL的交互阻抗模型

考慮鎖相環的影響，由式（9），（11）可得含有鎖相環的二者交互的正序阻抗模型為

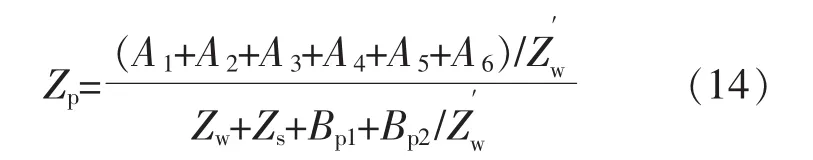
式中：Bp1和Bp2分別為直驅風電機組和SVG鎖相環參數與基頻電流、靜態工作點和電流環控制參數耦合環節。

2.3 穩定性判據

電網與風電機組之間的穩定性可由級聯系統穩定性判據[9]進行判斷。圖3所示為其等效阻抗網絡，ib和ug分別為理想電流源和理想電壓源。

圖3 直驅風電機組并網系統正序等效阻抗網絡Fig.3 The positive equivalent impedance model of DPMSGs integrated in a grid

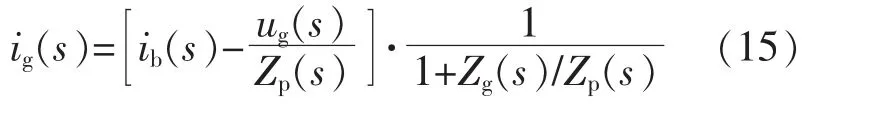
由式（15）可知，直驅風電并網系統穩定須滿足兩個條件：①1/Zp（s）穩定；②在電網阻抗一定的情況下，保證 Zg（s）/Zp（s）滿足奈奎斯特穩定性判據。由式（14）可知，控制參數的變化會引起輸出阻抗幅值和相位的變化和波動。因此，在輸出阻抗幅值變化的絕對值增大、相位波動性較大的頻段，如果不滿足上述穩定條件，系統發生振蕩的風險就會增大。

3 直驅風電機組模型驗證及阻抗特性分析

為了驗證上述分析建模的合理性，在Matlab平臺上建模。在分析過程中，將6臺直驅風電機組組成的風電場等值成一臺容量為9 MW的風電機組，其主要電氣及控制參數如表1所示。SVG的補償容量為±1 Mvar，參數如表2所示。鎖相環和電流環控制參數對系統運行特性的影響將直觀地體現于并網電流中。

表1 直驅風電機組網側變流器參數Table 1 Parameters of a grid-side converter in full-scale power converter turbine

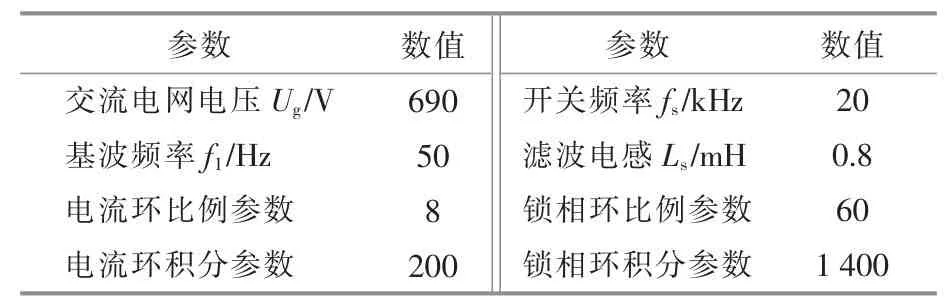
表2 靜止無功發生器參數Table 2 Parameters of a static var generator

3.1 SVG和鎖相環對輸出阻抗特性的影響

圖4為輸出阻抗特性曲線，通過對比Zwp和Zp可知，SVG投入后輸出阻抗幅值變小，這種阻抗的變化說明了SVG與直驅風電機組相互控制耦合，共同作用于系統的輸出阻抗。此外，由曲線Zp和Z可知，考慮鎖相環相對不考慮鎖相環時的輸出阻抗幅值變小。這是由于在考慮鎖相環后，阻抗模型的分母多出了兩項表達式者共同作用于阻抗模型的分母中，使得考慮鎖相環時的輸出阻抗減小，系統受擾后易出現不穩定的狀態。

圖4 SVG投入前后輸出阻抗波特圖Fig.4 Bode diagram of output impedance before and after the input of SVG

3.2 直驅并網系統阻抗特性分析及仿真驗證

3.2.1 鎖相環控制參數影響分析

通過阻抗模型（14）可知，鎖相環控制參數影響著直驅并網系統的輸出阻抗特性。圖5給出了3種情況下的輸出阻抗特性曲線：a-直驅風電機組控制參數正常 （kwp=60，kwi=1 400）；b-直驅風電機組鎖相環控制參數取值較小（kwp=0.1，kwi=150）；c-直驅風電機組鎖相環控制參數取值較小的前提下，投入鎖相環控制參數取值較小的SVG（kwp=0.1，kwi=150，ksp=0.1，ksi=150）。

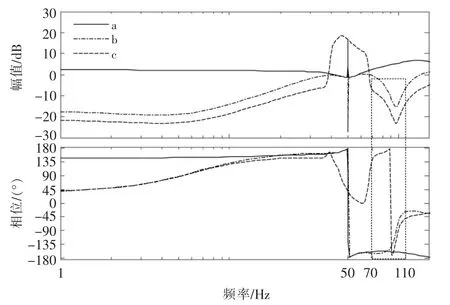
圖5 輸出阻抗波特圖Fig.5 Bode diagram of output impedance

由圖可知，b，c兩種條件下的輸出阻抗幅值在70～110 Hz減小的絕對值增大，相位出現較大波動性，由阻抗穩定性判據可知，相應頻段系統發生振蕩的風險增大。

為了驗證圖5中阻抗特性分析的正確性，本文對不同條件下直驅風電機組A相電流輸出波形和頻譜進行了分析，結果如圖6所示。

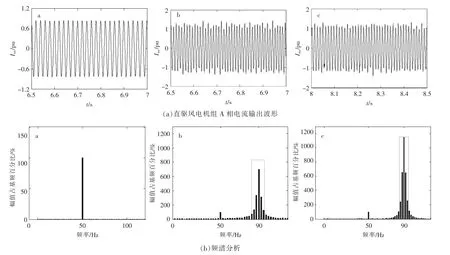
圖6 不同條件下直驅風電機組A相電流輸出波形和頻譜分析Fig.6 The current waveforms of a DPMSG with different situation and FFT analysis

由圖 6（a）可知，在 b，c 兩種情況下，直驅風電機組輸出電流波形均出現了振蕩現象。由圖6（b）可以看出：a條件下，系統中無次/超同步振蕩分量，處于穩定運行狀態；b條件下，系統中超同步頻率分量的含量較大，以90 Hz附近分量為主；c條件下，系統中90 Hz附近分量增加。

直驅風電機組鎖相環控制參數的取值主要影響超同步頻段，且當SVG的鎖相環控制參數取值較小時，會加劇超同步振蕩的風險。

3.2.2 電流環控制參數影響分析

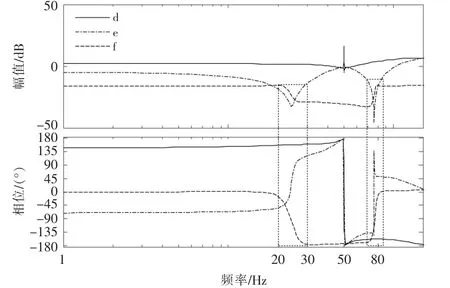
圖7 輸出阻抗波特圖Fig.7 Bode diagram of output impedance

電流環控制參數的取值也影響著輸出阻抗特性。圖7所示為3種條件下的輸出阻抗特性曲線：d-直驅風電機組控制參數正常（kwip=1，kwii=50）；e-直驅風電機組電流環比例參數取值較小 （kwip=0.01，kwii=50）；f-直驅風電機組電流環比例參數取值較小的前提下，投入電流環比例參數取值較小的 SVG（kwip=0.01，kwii=50，ksip=0.08，ksii=200）。

由圖7可知，e，f兩種條件下輸出阻抗幅值在20～30 Hz和80 Hz附近減小的絕對值增大，相位出現較大波動性，由阻抗穩定性判據可知，相應頻段系統發生振蕩的風險增大。圖8為不同條件下直驅風電機組A相電流輸出波形和頻譜分析。

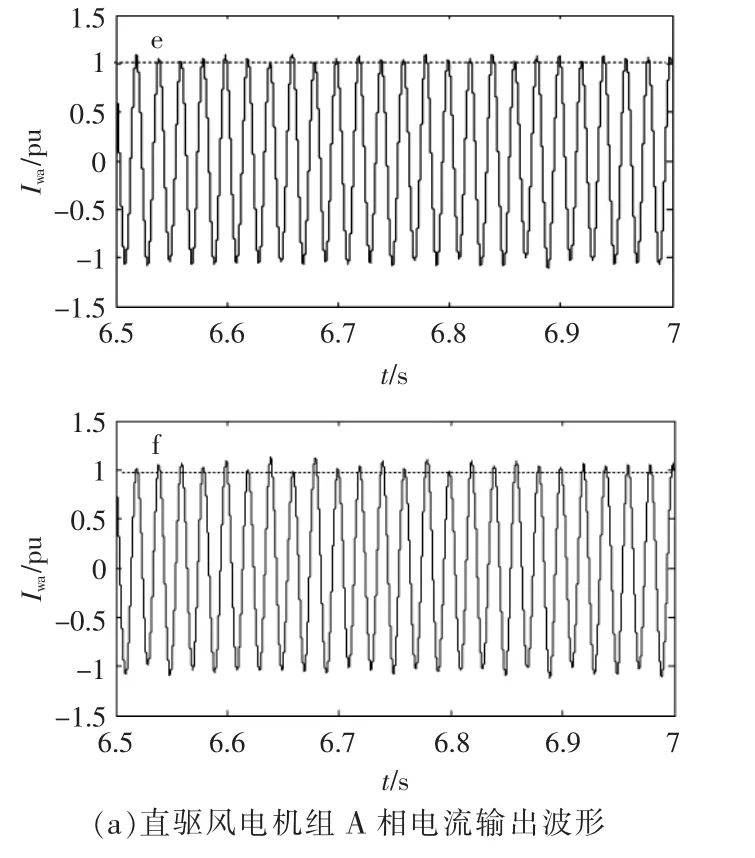
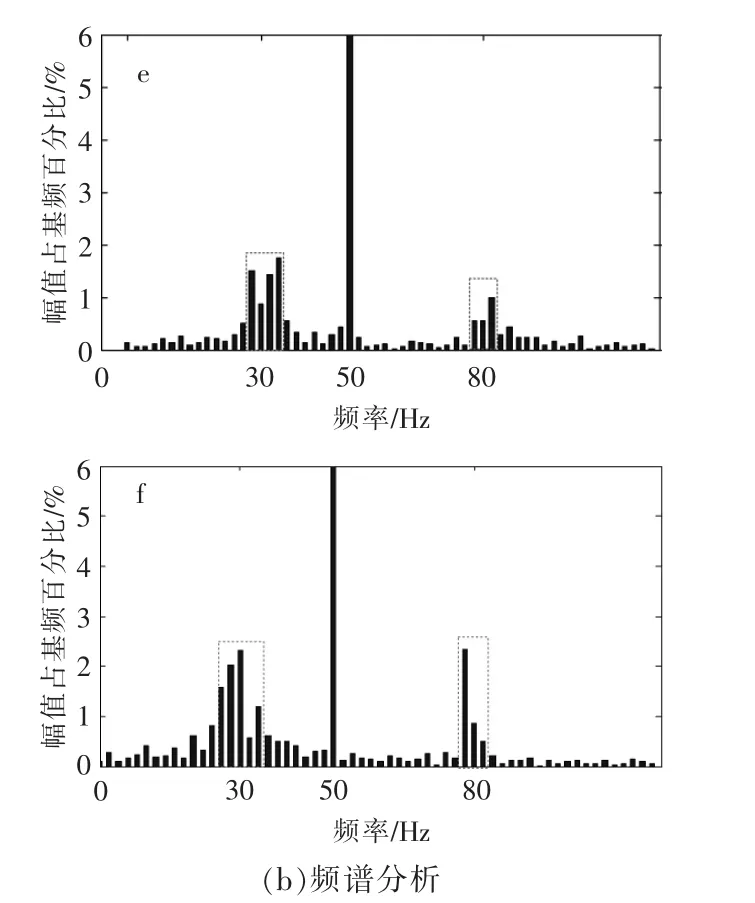
圖8 不同條件下直驅風電機組A相電流輸出波形和頻譜分析Fig.8 The current waveforms of a DPMSG with different situation and FFT analysis

由圖 8（a）可知，e，f兩種條件下并網電流輸出波形均出現了一定程度的振蕩。由圖8（b）可知，e條件下系統中出現了30 Hz和80 Hz附近分量。在此前提下，f條件下系統中30 Hz和80 Hz附近分量的含量則會增大。

直驅風電機組電流環比例參數的取值對次/超同步頻段都有影響，且投入的SVG電流環比例參數取值較小時，會加劇振蕩。相對于鎖相環控制參數的取值對系統穩定性造成的影響，電流環比例參數取值的影響要更小一些。

4 結論

本文推導了含鎖相環的直驅風電機組與SVG交互作用的正序阻抗模型，研究了二者交互作用引起的次/超同步振蕩問題，得出以下結論。

①SVG的投入減少了直驅風電機組的輸出阻抗，二者控制參數相互耦合，共同影響著并網系統的輸出阻抗特性。

②直驅并網系統鎖相環和電流環控制參數對其輸出阻抗特性有著不同程度的影響，這些參數設置不當，會激發系統振蕩的風險。直驅風電機組鎖相環控制參數的取值主要影響超同步頻段，當SVG的鎖相環控制參數設置不當時，會加劇系統超同步振蕩的風險。直驅風電機組電流環比例參數的取值對次/超同步頻段都有影響，當投入的SVG電流環比例參數設置不當時，會加劇系統振蕩。