無源時差定位系統最優布站方法研究

(西安電子科技大學電子信息攻防對抗與仿真技術教育部重點實驗室， 陜西西安 710071)

0 引言

無源定位系統被廣泛應用于環境監測、醫療和軍事等領域，其基本原理是通過測量目標輻射源的發射信號，對目標進行定位。常用的無源定位技術有：基于到達時間(Time of Arrival , TOA)、到達時間差(Time Difference of Arrival, TDOA)、到達角度(Angle of Arrival, AOA)、到達頻率差(Frequency Difference of Arrival,FDOA)等[1]。其中，TDOA技術因其較高的定位精度得到廣泛的研究和應用。當定位技術確定時，影響定位精度的主要因素有基站布局、時差測量誤差、布站誤差等[2]。本文主要研究在不同時差測量誤差影響下的TDOA定位系統的最優布站方法。

目前研究各種無源定位系統布站方法的文獻中，大多是使用解析法，假設TDOA測量誤差為恒定高斯分布，理論推導后得到基站在一些特定位置時的布站方法，其求解較復雜且不具有普遍適用性。如文獻[3]通過半正定規劃的方法研究了傳感器網絡中最優定位節點的選擇。文獻[4]研究了直線、梯形、平行四邊形、長方形、菱形、倒三角、正方形和Y形八種規則布站時的定位誤差，指出Y形布站覆蓋范圍最大，各個方向定位精度較好。文獻[5]通過對克拉美羅下界的跡的表達式推導得到：當接收站包圍目標并呈等角布站時布站最優。文獻[6]通過改變規則圖形布站的基線長度和基線指向，研究了不規則布站的布站策略。文獻[7]將TDOA系統布站問題轉化為最優化問題進行求解，使用遺傳算法(Genetic Algorithm , GA)來求解最優布站，具有普遍適用性，但是該方法仍然是假設TDOA測量誤差為恒定高斯分布，未考慮基站和目標的位置、目標信號帶寬、接收機噪聲帶寬等因素對TDOA測量誤差的影響，而且遺傳算法調節參數較多，收斂速度較慢，需要較多次迭代才能解得最優布站位置。

針對以上問題，本文以TDOA無源定位系統為研究對象，求解出更符合實際情況的TDOA測量誤差，并在此基礎上用粒子群算法(Particle Swarm Optimization，PSO)求解指定范圍內的最優布站位置。

1 三維空間TDOA定位模型

假設在三維空間中，待定位目標輻射源位置為x=[x,y,z]T，接收基站位置si=[xi,yi,zi]T，i=0,1,…,n，表示為向量形式為s=[s0,s1,…,sn]T，輻射源到接收站的歐氏距離為ri=‖x-si‖，i=0,1,…,n。設定s0為主接收基站，輻射源信號傳播速度為c，可得式(1)：

ri0=cti0=Δri0+cni0,i=1,2,…,n

(1)

式中，ri0為實際測得的第i號基站與主站到目標輻射源距離的差值，ti0為實際測得的第i號基站與主站到目標輻射源的時差，Δri0為第i號基站與主站在不含測量誤差情況下到目標輻射源距離的差值，ni0為第i號基站與主站的實際時差測量誤差。

將式(1)表示為向量形式：

z=h(x)+e

(2)

式中，z=[r10,r20,…,rn0]T，e=[cn10,cn20,…,cnn0]T,h(x)=[r1-r0,r2-r0,…,rn-r0]T。

三維空間TDOA定位即是在已知接收站的位置和測量時差的基礎上，對目標的位置u進行求解。

2 不同TDOA測量誤差下定位精度的CRLB分析

在無源時差定位問題中，目標的定位誤差會存在CRLB。CRLB的跡表示了無偏的目標位置估計量在各個維度上方差的和，工程中一般以它來衡量目標定位性能。在定位方法一定時，TDOA測量誤差的計算方式不同，會影響CRLB的求解。

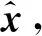
(3)

F為Fisher信息矩陣：

F=E{[xlnp(z|h(x))][xlnp(z|h(x))]T}

(4)

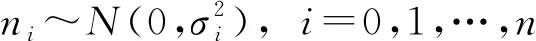
CRLB=F-1=(QTR-1Q)-1

(5)

式中，

(6)

R=cov(e·eT)=

(7)

假設σ0=σ1=…=σn=σs時，

(8)

實際應用中，基站的觀測性能受多種因素的影響，此時可將TDOA測量誤差的方差視為由目標信號參數、信噪比和傳播距離等決定的一個函數，表示為：ni0～(0,σ2(x)),i=1,2,…,n，因此提出一種更接近實際情況的計算CRLB的方法。假設三維空間TDOA定位模型在視距環境中，則第i個基站接收信號的功率可由電磁波在自由空間的傳播損耗模型來確定[9]：

(9)

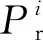
(10)

SNR為某一參考距離r處的信噪比，則第i個定位基站處接收信號的信噪比可以表示為

(11)

由TDOA測量相關理論可知，當多種可用技術用于測量TDOA時，該估計將是無偏的而且其方差可以達到時差測量的CRLB[10]。利用互相關法測量信號時間差的精度極限可以表示為[11]

(12)

式中，B為接收信號的均方根等效帶寬，Bn為噪聲信號的均方根等效帶寬，T為信號相對于采樣周期的時間長度，SNRi0為相關后信號對噪聲的功率比，兩者都是無單位的比值。SNRi0可表示為

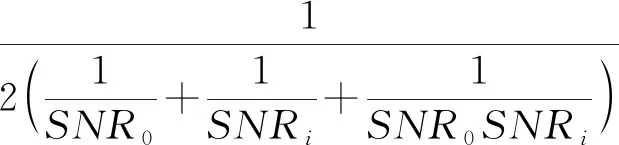
i=1,2,…,n

(13)

式(11)和式(13)代入式(12)中可得第i號基站和主站所測輻射源信號的TDOA下界為

(14)

由式(14)可以看出,TDOA測量誤差與目標輻射源和基站間的距離、目標信號帶寬，目標信號累積時間、接收機的噪聲帶寬、參考距離及其對應信噪比有關。

此時假設主站和不同基站間的TDOA測量誤差相互獨立，則測量向量z的似然函數為

(15)

此時，距離誤差的協方差矩陣為

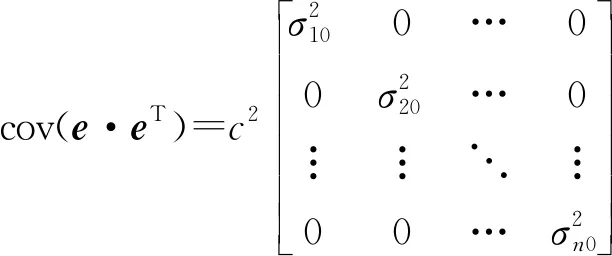
(16)

將式(15)代入式(4)中，可得F的各個元素為

Fij=(QTR(x)-1Q)ij+

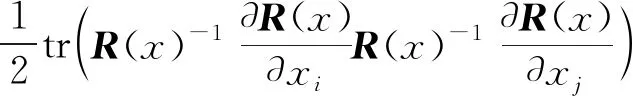
(17)

其中，Q可以用式(6)來表示。則有

(18)

則CRLB的跡為

J=tr(CRLB)=tr(F-1)

(19)

3 基于粒子群算法的最優布站方法

在求解最優布站位置時，輻射源目標的具體位置是未知的，為確保目標區域的整體定位精度，本文采用的方法是將目標區域離散化，目標區域的整體定位精度可以表示為

(20)

式中，θ=[x0,y0,z0,x1,y1,z1,…,xn,yn,zn]為參與定位的n+1個基站的位置，N為目標區域內的輻射源目標個數。則在基站指定布站區域內，用粒子群算法對目標函數f(θ)迭代尋優，使函數f(θ)的值最小時的變量θ即為基站的最優布站位置。粒子群算法求解最優布站流程為：

1) 種群初始化：隨機產生規模為M個粒子的種群，設定迭代次數、在布站區域內初始化粒子θ中每個基站的三維坐標位置和坐標移動速度。

2) 根據目標函數f(θ)計算每個粒子的定位誤差，獲取粒子個體的歷史最佳位置、種群的歷史最佳位置、個體最佳適應度、種群最佳適應度。粒子定位誤差越小，其適應度越高，布站位置越好。

3) 按粒子群算法粒子更新公式[12]更新粒子位置和速度，繼續執行流程2)，直到迭代到指定次數。迭代后所求得的適應度最高的粒子即為最優布站位置，其對應的函數值即為定位誤差。

4 算法仿真和結果分析

本節主要是采用粒子群算法，對三維空間中不同TDOA測量誤差下最優布站位置和布站性能進行仿真和分析。仿真參數設置為：

1) 定位系統參數：定位基站個數為4，基站區域為R1:{x∈[-25,25],y∈[-25,25],z∈[0,5]}，目標區域為R2:{x∈[-100,200],y∈[0,200],z∈[5]}，單位為km。信號等效帶寬B=500 kHz，噪聲等效帶寬Bn=1 MHz，時間長度T=1 000，參考距離r=100 m處的信噪比為30 dB，即SNR=1 000。

2) 粒子群算法參數：種群規模為200，最大迭代次數為200次，變量維數為12，自我學習因子c1=1.5，群體學習因子c2=1.5，慣性權重ω取0.9～0.4，隨迭代次數的增加線性遞減。

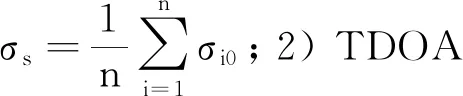
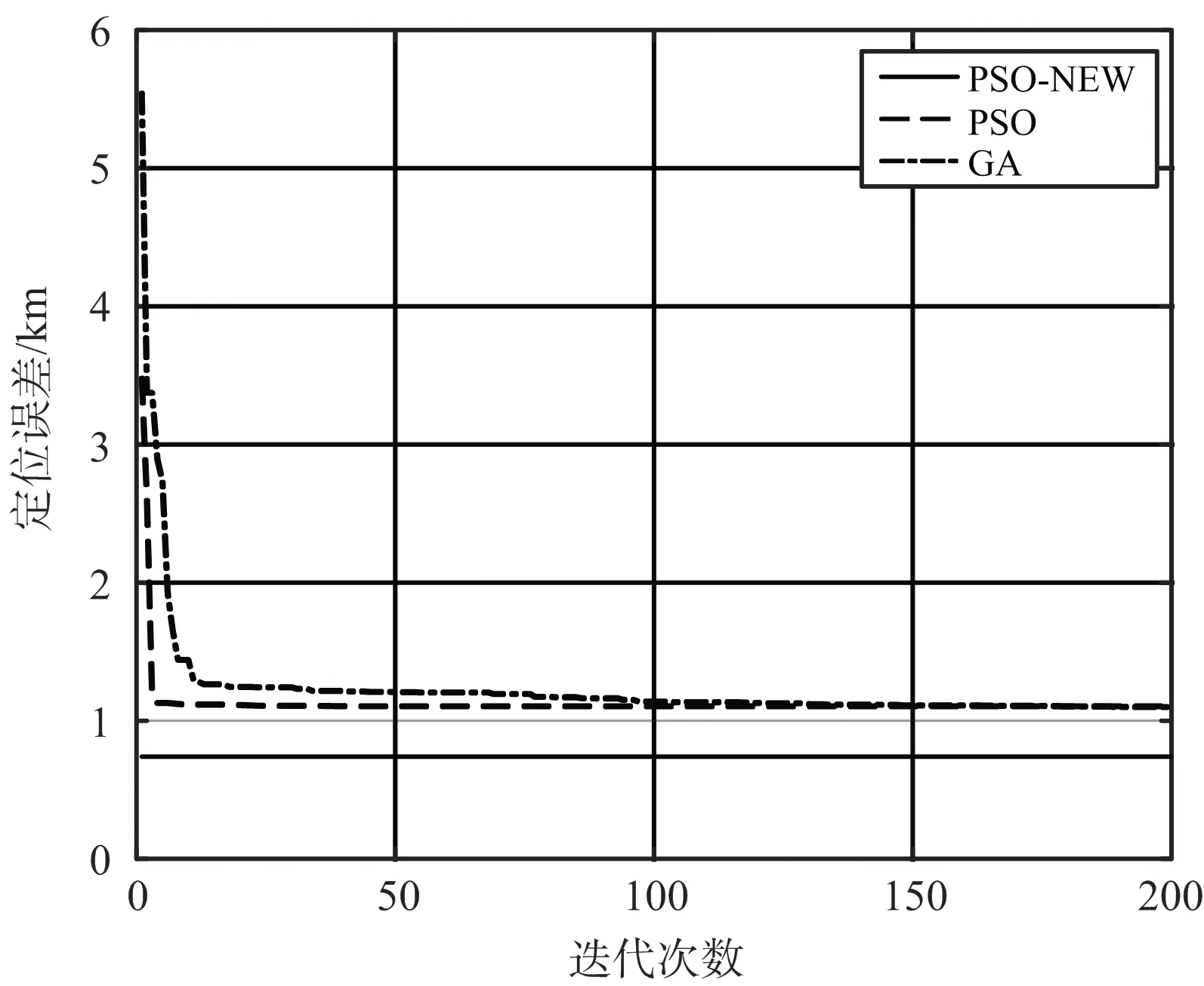
圖1 不同迭代次數后基站最優布站時的定位誤差

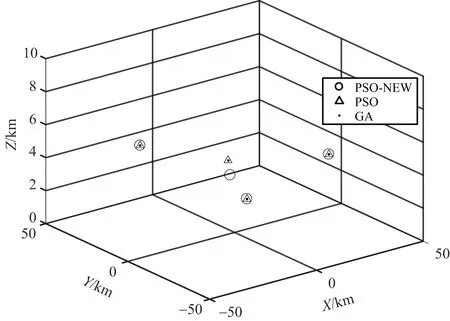
圖2 迭代200次后最優布站的位置

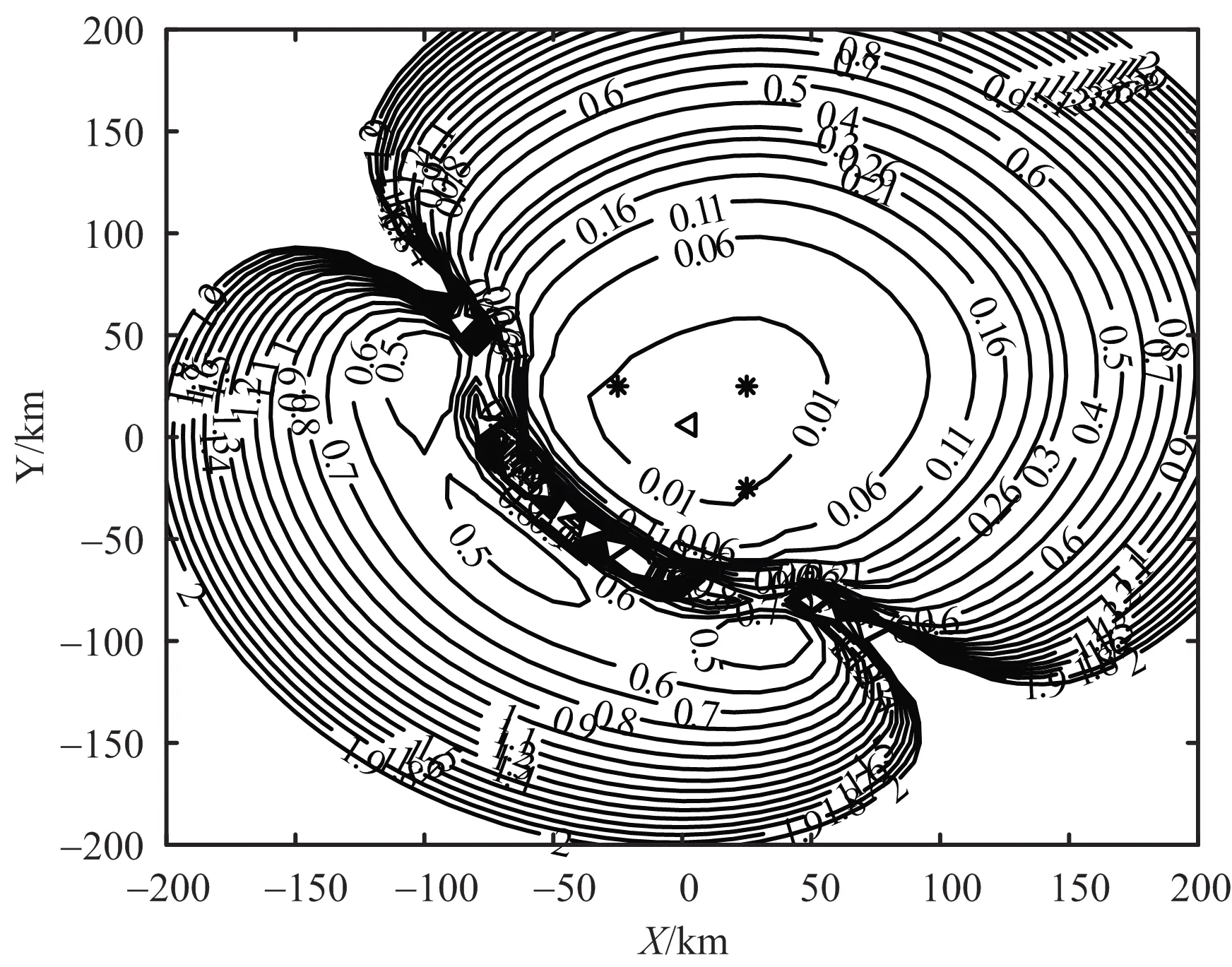
圖3 PSO-NEW算法最優布站時定位誤差等高線圖

圖1為隨迭代次數的增加，3種算法求解得到的基站最優布站對目標區域的定位誤差。圖2為迭代200次后，3種算法求解后得到的最優布站三維坐標圖，不同算法求解得到的基站位置用不同形狀的圖形來區分。從圖1可以看出：當TDOA測量誤差為恒定高斯分布時，粒子群算法(PSO)比遺傳算法(GA)收斂速度更快，更適用于需要快速作出反應的無源定位環境，兩者定位精度基本相同。從圖2可以看出：當TDOA測量誤差為恒定高斯分布時，PSO算法和GA算法求解的最優布站位置基本相同。從圖1還可以看出：當TDOA測量誤差為多種因素綜合影響的函數時，用PSO算法求得最優布站所對應的定位誤差與TDOA測量誤差為恒定高斯分布時相比，定位誤差由1.092 5 km下降到0.529 81 km，說明此時求解的最優布站位置更好，可以實現對目標區域更高精度的定位。

圖3為PSO-NEW算法200次迭代后求得的最優布站位置所對應的定位誤差CRLB的等高線圖，從圖中可以看出，目標區域R2內，定位誤差以布站區域為中心向四周逐漸遞增，目標區域的定位誤差基本都在2 km以內，進一步證明本文所提算法求得的布站位置對目標區域的整體定位性能良好。

5 結束語

本文研究了三維時差定位系統模型，提出了一種更符合實際情況的TDOA測量誤差的計算方法，并推導出在不同時差測量誤差影響下，目標區域定位誤差的CRLB。本文以定位誤差CRLB的跡的平均值最小為優化目標，用粒子群算法求解最優布站。仿真結果表明：本文所提算法求解的最優布站位置，與假設TDOA測量誤差為恒定高斯分布時相比，其定位誤差明顯減小，目標區域整體定位性能良好；與用遺傳算法求解的最優布站位置相比，其收斂速度快且調節參數少，更適用于需要快速作出反應的偵察定位場合；同時，本文所提算法無需像解析法中那樣針對特定情況推導最優布站位置，在理論上可以求解在任意布站區域內的最優布站，求解簡單且具有普遍適用性。