基于廣義梯度矢量流模型圖像分割算法的研究
王晨霞 于明
摘要 梯度矢量流模型(GVF)是引導主動輪廓模型形變的有效外力,但不能分割細長凹陷區域,因此提出廣義梯度矢量流(GGVF)模型。GGVF模型將GVF模型中的常數系數替換為兩個變化的權重函數,雖然擁有較好的細長凹陷收斂能力,但仍然在進入復雜凹陷、保護弱邊緣、抵抗噪音方面存在局限性。為了解決這些問題,在GGVF模型的基礎上做了3點改進:1)在構建邊緣圖時引入雙邊濾波器用于平滑噪音;2)用散度算子替代拉普拉斯算子實現更好的凹陷收斂能力;3)添加方向約束函數用于保護弱邊緣。實驗結果表明,該算法具有較好的性能,且相對于傳統GGVF模型,召回率提高15.6%,F1值提高8.7%。
關 鍵 詞 圖像分割;主動輪廓模型;梯度矢量流模型;散度算子;雙邊濾波
中圖分類號 TP391 ? ? 文獻標志碼 A
主動輪廓模型,即Snake算法,自1987年被Kass等[1]提出后,就被廣泛應用于圖像分割領域。它將平面中曲線向目標物體的演化轉化為極小化能量泛函的過程。該能量泛函可被分為內部能量和外部能量兩部分,內部能量用來約束曲線的形狀,外部能量則可以吸引曲線向目標邊界移動。傳統Snake模型中,外力來源于圖像梯度,這種外力場捕捉范圍很小,因此必須將初始輪廓的位置設置在目標附近時才能使其收斂到正確位置,而對于凹陷區域,這種外力場也無能為力。1998年,Xu等[2]提出梯度矢量流主動輪廓模型(GVF Snake),把圖像邊緣處的梯度矢量向周圍進行擴散,在同質區域產生一緩慢變化的外力場,擴大捕獲范圍的同時在一定程度上也能抑制噪聲的影響。盡管GVF Snake 模型相對傳統Snake模型做了很大的改善,但是仍然存在著一些缺陷,例如難以進入細長凹陷區域,存在弱邊緣泄露問題,對椒鹽噪聲比較敏感。因此,許多專家學者們紛紛針對梯度矢量流(GVF)模型中存在的缺陷提出改進方法[3-12]。例如,文獻[3]提出廣義梯度矢量流(GGVF)模型,該模型采用兩個變化的權重函數分別作用于梯度矢量流模型的平滑項和保真項,使得修改后的GGVF模型可以自適應地平衡兩者的擴散程度,改善了模型的細長凹陷收斂能力。文獻[4]提出成分歸一化的廣義梯度矢量流(CNGGVF)模型,該模型用成分歸一化的方法替代傳統矢量歸一化的方法,在GGVF模型的基礎上進一步改善了模型深度凹陷收斂的能力。文獻[7]提出導向濾波梯度矢量流(GFGVF)模型,該模型通過改寫邊緣圖和權重函數,進一步改善了模型的邊緣保護能力。
在本文中,提出一個基于傳統GGVF的改進模型,旨在改善模型的整體功能,包括噪聲魯棒性、深度凹陷收斂性能和弱邊緣保護性能。本文的主要貢獻包括以下幾個方面。
1)引入雙邊濾波器用以構建新的邊緣圖。雙邊濾波可以同時具有保持邊緣、降噪平滑的作用.這在一定程度上解決了邊緣泄漏弱的問題。因此,雙邊濾波具有更好的濾波效果。
2)用散度算子去替代拉普拉斯算子。這樣可以改變梯度矢量從邊緣區域到同質區域的擴散方式,繼而可以改善新模型對凹陷區域的收斂性能。
3)添加方向約束函數。這樣可以使得邊緣處的擴散是沿垂直于梯度的方向進行而不是跨越邊緣方向,因此弱邊緣可以得以有效保留。
1 Snake,GVF和GGVF模型
1.1 Snake模型
1987年Kass等[1]首次提出Snake模型,它實際上是描述一個連續的閉合曲線[c(s)=(x(s),y(s))],[s∈[0,1]],在圖像空間域中的演化過程可以用最小化以下能量函數來表示:
1.2 GVF Snake模型
為了克服傳統Snake模型的兩個關鍵性局限,Xu等[2]提出GVF模型,用來替代傳統Snake模型的外力,它可以表示為一個向量場[v(x,y)=[u(x,y),v(x,y)]],通過極小化如下能量泛函得到:
GGVF模型具有自適應擴散的能力,在式(7)中,第一項為平滑項,主要作用在同質區域,具有各向同性的平滑效果。第二項為數據項,主要作用在邊緣區域附近,使得到的力場盡可能接近圖像梯度矢量。參數[k]的作用與GVF模型中[μ]的作用類似。
2 新模型的提出
2.1 引入雙邊濾波器構造新的邊緣圖
在實際應用中,為了減少噪音的干擾,往往會對原圖進行濾波處理。傳統的濾波器,如高斯濾波會在平滑噪音的同時將邊緣信息也模糊掉。而文獻[13]提出的雙邊濾波器通過結合距離差異權重和灰度值差異權重很好地解決了這一問題,式(10)、式(11)給出了雙邊濾波的操作過程,[Iq]為輸入圖像,[Ibf]為濾波后圖像。
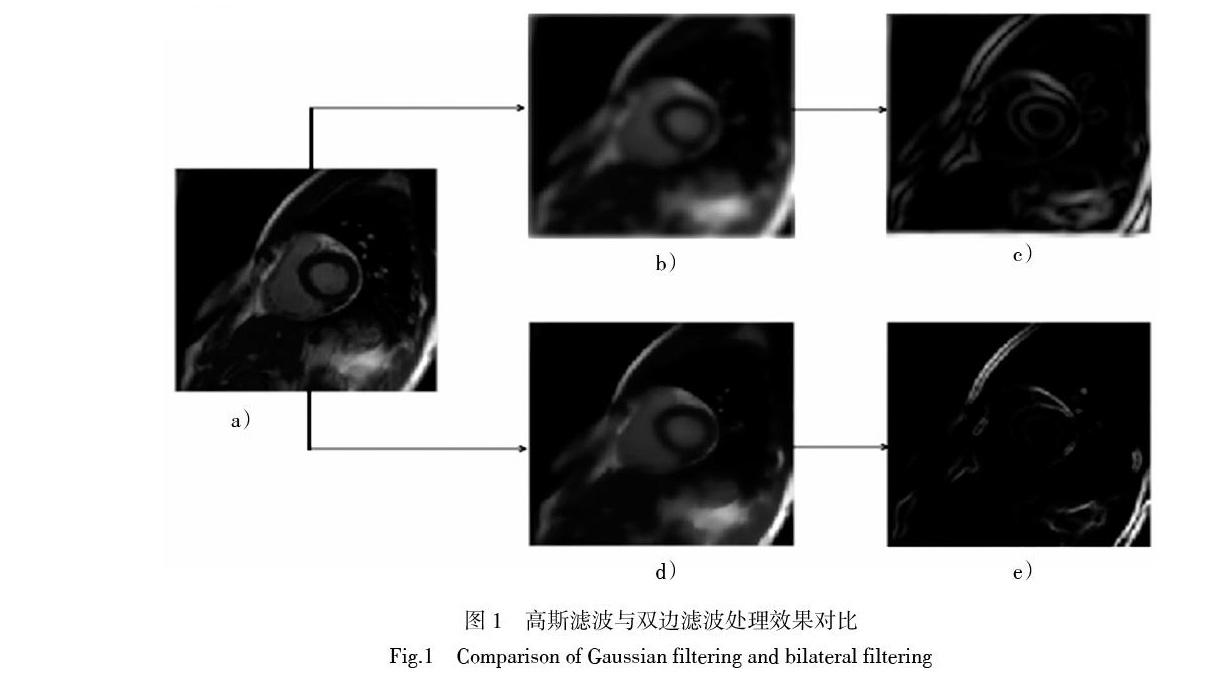
式中:[σs]為空域高斯函數的標準差;[σr]為值域高斯函數的標準差。在同質區域,[Ip-Iq]的值變化很小,對應的值域權重接近于1,此時空域權重起主要作用,相當于直接對此區域進行高斯模糊。在邊緣區域,[Ip-Iq]會有較大的差異,此時值域權重會下降,從而導致此處整個核函數的分布的下降,而保持了邊緣的細節信息。在此基礎上,新的邊緣圖可以通過[e(x,y)= ? ?I(x,y)bf]得到。圖1給出了分別經過高斯濾波和雙邊濾波處理的效果,其中圖1a)為輸入圖像,圖1 b)和d)分別為經過高斯濾波和雙邊濾波處理后的輸出圖像, 圖1c)和e)分別為對應 圖1b)和d)得到的邊緣圖。如圖1所示,輸入圖像經過高斯濾波處理后,噪音可以被平滑,但是邊緣圖中的邊緣信息也被模糊了。然而在經過雙邊濾波器處理之后,邊緣圖中的邊緣仍然清晰可辨。
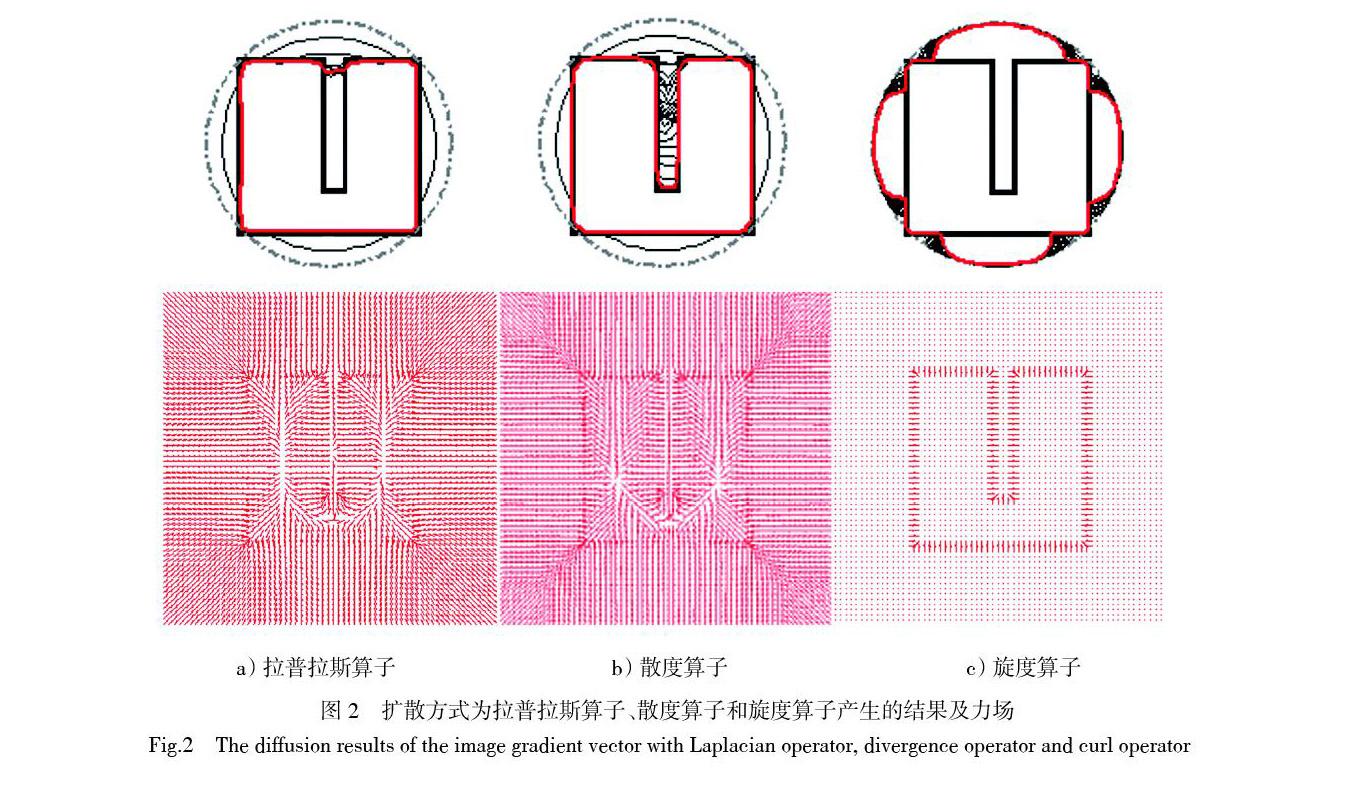
2.2 用散度算子替代拉普拉斯算子
由第1.2節分析可知,GVF模型中邊緣梯度矢量的擴散主要依賴于平滑項中的拉普拉斯算子。根據亥姆霍茲定理,任意矢量場可以分解為無散量和無旋量。因此,拉普拉斯算子的能量函數可以被拆分為
算法性能的主觀評價具有一定的局限性,為了進一步評估算法分割的準確性,本文采用精確率(Precision)、召回率(Recall)和F1值對實驗結果進行客觀評價,分別定義為
式中:[Mseg]和[Gseg]分別表示算法分割得到的對象區域和真實輪廓包含的對象區域。當上述3種度量均為1時,表示由算法得到的對象區域與標準對象區域完全重合,更詳細的信息可見文獻[16-18]。在表1中,給出GVF、GGVF、NGVF、CNGGVF、GFGVF和新模型分割5副醫學圖像得到結果的定量評價值,并計算出每個模型關于5副醫學圖像分割結果的平均指標。仔細觀察表中數據,可以得到以下結論:1)在所有醫學圖像中,新模型具有最高的F1值;2)最后一列的平均評價指標表明新模型具有最高的召回率和F1值;3)與傳統GGVF模型相比,新模型增加了約15.6%的召回率和8.7%的F1值。因此,從客觀評價角度分析,本文提出的方法能夠更準確地分割醫學圖像中的目標區域。
4 結語
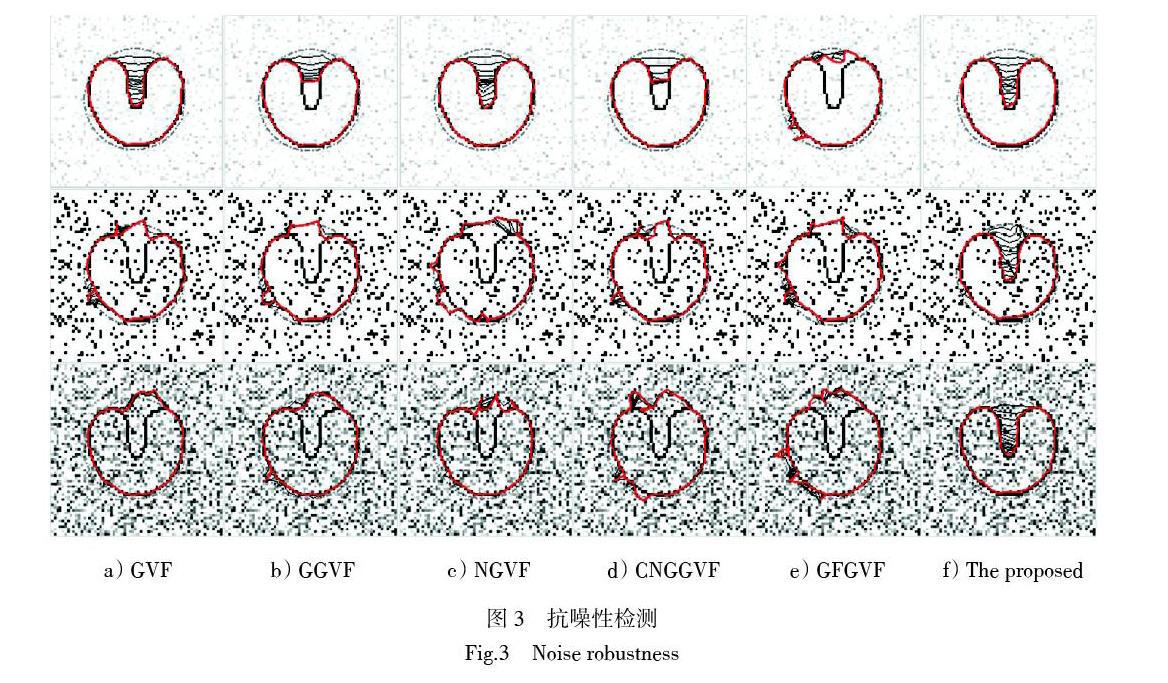
基于傳統GGVF模型在進入復雜凹陷,保護弱邊緣,抵抗噪音方面存在的局限,提出了一種新的主動輪廓外力,它結合使用了雙邊濾波器,散度算子和方向約束函數。為了評價所提出模型的性能,將其與GVF、GGVF、NGVF、CNGGVF和GFGVF模型進行了比較。人工合成圖像的實驗結果表明,該模型在噪聲魯棒性,深度凹陷收斂性能和弱邊緣保護方面優于傳統模型。另外,新模型還被用于醫學圖像分割,并且定量和定性的實驗結果顯示其相對于其他傳統模型具有更準確的分割結果。
參考文獻:
[1] ? ?KASS M,WITKIN A,TERZOPOULOS D. Snakes:Active contour models[J]. International Journal of Computer Vision,1988,1(4):321-331.
[2] ? ?XU C,PRINCE J L. Gradient vector flow:a new external force for snakes[C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR). San Juan,Puerto Rico,1997:66-71.
[3] ? ?XU C Y,PRINCE J L. Generalized gradient vector flow external forces for active contours[J]. Signal Processing,1998,71(2):131-139.
[4] ? ?QIN L M,ZHU C,ZHAO Y,et al. Generalized gradient vector flow for snakes:new observations,analysis,and improvement[J]. IEEE Transactions on Circuits and Systems for Video Technology,2013,23(5):883-897.
[5] ? ?祝世平,高瑞東. 基于自適應擴散梯度矢量流的圖像分割算法[J]. 光電子·激光,2015(12):2409-2416.
[6] ? ?張靜林,高紅,馬寶英. 一種改進的梯度矢量流Snake側腦室分割算法[J]. 中國醫學物理學雜志,2015,32(5):711-716.
[7] ? ?ZHAO F,ZHAO J,ZHAO W D,et al. Guide filter-based gradient vector flow module for infrared image segmentation[J]. Applied Optics,2015,54(33):9809-9817.
[8] ? ?ANANTH C,KARTHIKA S,SINGH S. Graph Cutting Tumor Images[J]. Social Science Electronic Publishing,2017,4(3):309-314.
[9] ? ?鄒北驥,張思劍,朱承璋. 彩色眼底圖像視盤自動定位與分割[J]. 光學 精密工程,2015,23(4):1187-1195.
[10] ?REN D W,ZUO W,ZHAO X F,et al. Fast gradient vector flow computation based on augmented Lagrangian method[J]. Pattern Recognition Letters,2013,34(2):219-225.
[11] ?NAKHMANI A,TANNENBAUM A. Self-crossing detection and location for parametric active contours[J]. IEEE Transactions on Image Processing,2012,21(7):3150-3156.
[12] ?GUO Q,SUN S F,REN X H,et al. Frequency-tuned active contour model[J]. Neurocomputing,2018,275:2307-2316.
[13] ?TOMASI C,MANDUCHI R. Bilateral filtering for gray and color images[C]//Sixth International Conference on Computer Vision (IEEE Cat. No. 98CH36271),Bombay,India. Narosa Publishing House,1998:839-846.
[14] ?LI C M,LIU J D,FOX M D. Segmentation of external force field for automatic initialization and splitting of snakes[J]. Pattern Recognition,2005,38(11):1947-1960.
[15] ?LI Q,DENG T Q,XIE W. Active contours driven by divergence of gradient vector flow[J]. Signal Processing,2016,120(3):185-199.
[16] ?FERGANI K,LUI D,SCHARFENBERGER C,et al. Hybrid structural and texture distinctiveness vector field convolution for region segmentation[J]. Computer Vision and Image Understanding,2014,125:85-96.
[17] ?ESTRADA F J,JEPSON A D. Benchmarking image segmentation algorithms[J]. International Journal of Computer Vision,2009,85(2):167-181.
[18] ?ZHU S P,BU X Y,ZHOU Q. A novel edge preserving active contour model using guided filter and harmonic surface function for infrared image segmentation[J]. IEEE Access,2018,6:5493-5510.
[責任編輯 田 豐]

