密閉空間可燃氣體爆炸超壓預測*

秦 毅，陳小偉，黃 維

（1. 北京理工大學爆炸科學與技術國家重點實驗室，北京 100081；2. 北京理工大學機電學院，北京 100081；3. 重慶科技學院安全工程學院，重慶 401331；4. 中國工程物理研究院總體工程研究所，四川 綿陽 621999；5. 北京理工大學前沿交叉科學研究院，北京 100081 ）

可燃氣體因熱能高、來源廣、污染小等優點而被廣泛使用，但在其使用、儲存和運輸過程中會與空氣混合形成預混可燃氣體，在適當條件下易發生燃燒爆炸事故，尤其是在密閉空間內，由于受到壁面的約束，爆炸后密閉空間內壓力迅速升高并形成沖擊波，導致結構破壞、破片散射和熱輻射等，從而造成嚴重的財產損失和人員傷亡。為了避免事故的發生或擴大，準確的爆炸超壓預測是進行結構抗爆設計和日常安全管理的關鍵，尤其是密閉空間爆炸時所產生的峰值超壓是抗爆設計和日常安全管理工作中最重要的參數之一。學者們對密閉空間內爆炸超壓已進行了相關研究[1-3]，對爆炸超壓及影響因素有了較為全面的了解。

受實驗安全性和經濟條件影響，現階段主要采取小尺寸實驗、理論分析和數值模擬相結合的方式對爆炸火焰傳播及超壓進行研究。在實驗研究和數值模擬方面，管道中爆炸火焰傳播及爆炸超壓分析是目前所進行的最為廣泛的研究，其研究內容主要圍繞管道內障礙物、形狀及長徑比等對爆炸火焰傳播影響的加速機理及超壓進行[4-6]；針對其他容器內的爆炸火焰傳播和超壓分析，主要以20 L 球為背景，開展了不同氣體、不同濃度、不同點火方式、不同點火能等對爆炸超壓及升壓速率的影響[1,7-8]。在理論分析方面，主要針對爆炸火焰的加速機理、爆炸火焰傳播過程中的不穩定性、爆燃轉爆轟的臨界條件等進行了分析[9-11]。

通過現有的研究可以看出：對密閉空間內可燃氣體爆炸超壓分析是以大量的小尺寸實驗為主，且更多的研究者更加關注最大峰值超壓，對壓力變化過程關注較少；數值模擬可對各種條件下的爆炸超壓及壓力變化過程進行分析，但模擬多以偏微分方程的形式體現，求解過程較為復雜，且模擬過程耗時較長，對工程應用而言存在一定的難度。本文中針對不同體積密閉空間內爆炸火焰傳播及超壓預測，在利用層流光滑火焰傳播速度分析的基礎上，分析火焰的不穩定性及所造成的褶皺及湍流火焰的形成。在此基礎上，利用分形燃燒理論建立較大體積時密閉空間爆炸超壓預測模型，可對不同體積密閉空間結構抗爆設計及安全管理提供參考。

1 光滑層流火焰傳播爆炸超壓預測

1.1 基本假設

密閉空間內可燃氣體爆炸時，其爆炸過程非常復雜，涉及流體力學、熱力學及燃燒學等多方面內容的交叉。為簡化數學模型和快速計算，先作如下假設[12]：（1）爆炸過程是在絕熱壁面條件下進行的；（2）初始可燃預混氣體和燃燒產物均符合理想氣體狀態方程；（3）整個密閉空間內部各處壓力是一致的；（4）可燃預混氣體溫度和燃燒產物溫度在爆炸發展過程中始終保持不變；（5）可燃預混氣體在容器中完全均勻分布且在球形容器中心點火；（6）忽略壓力上升對火焰傳播速度的影響。

1.2 控制方程

可燃預混氣體在爆炸過程中始終滿足質量守恒，其質量守恒方程可表示為：

式中：m 為初始預混氣體總質量，mu為未燃預混氣體質量，mb為已燃預混氣體質量，nu為未燃預混氣體摩爾數，nb為已燃產物摩爾數，Mu為未燃預混氣體摩爾質量，Mb為燃燒產物摩爾質量，Vu為未燃預混氣體體積，Vb為燃燒產物體積，V 為容器總體積。

在整個爆炸過程中，未燃預混氣體和燃燒產物狀態方程可表示為：

式中：P 為密閉空間壓力，R 為氣體常數，Tu為未燃預混氣體溫度，Tb為燃燒產物溫度。

密閉空間內可燃氣體被點燃后，表面光滑球形火焰以層流火焰傳播速度SL向前傳播時，單位時間內未燃預混氣體質量變化率可表示為：

式中：A 為火焰前鋒面表面積，t 為時間。

基于Lewis 等的燃燒過程中未燃氣體質量分數與壓力的關系為[13]：式中：Pe為氣體絕熱爆炸時的最終爆炸壓力。

將式（5）對時間t 進行求導，可得壓力隨時間的變化率與未燃預混氣體質量變化率的關系式為：

在爆炸反應開始之前，初始預混氣體狀態方程可表示為：

式中：n0為初始預混氣體摩爾數。

因此，初始預混氣體總質量 m 可表示為：

將式（4）、（8）代入式（6），則可得壓力隨時間的變化率為：

在爆炸反應過程中，假設最終的燃燒產物摩爾數與初始預混氣體的摩爾數基本相等[14]，即：n0=ne。此時，密閉空間內可燃預混氣體絕熱爆炸時的最終爆炸壓力可表示為：

1.3 爆炸超壓模型及結果分析

密閉空間內可燃預混氣體被點火源點燃后，立即形成中心火源，在周圍形成的燃燒波以球面波的形式向四周傳播，形成球形火焰。當t 時刻火焰前鋒面傳播位置到達r 時，燃燒產物占據的空間體積可表示為：

此時，球形火焰前鋒面表面積可表示為：

同時，將式（2）代入式（3），可得：

由式（13）可得：

將式（14）代入式（12），可得：

將式（15）代入式（9），可得球形密閉空間內爆炸壓力上升速率：

對式（16）進行變化，可得：

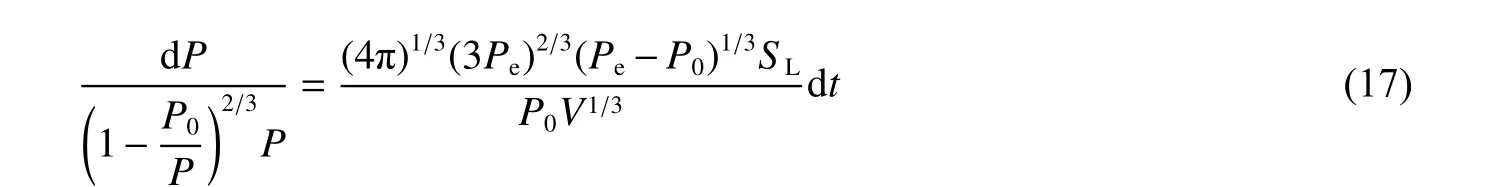
她丈夫從小跟著父親在這店鋪里學手藝，學成后就接手這店鋪，一直做到現在。“早些年村里人多，一天到晚忙不過來，喝口茶的工夫也沒有，現在村里人少了，一天掙不了幾個錢。”

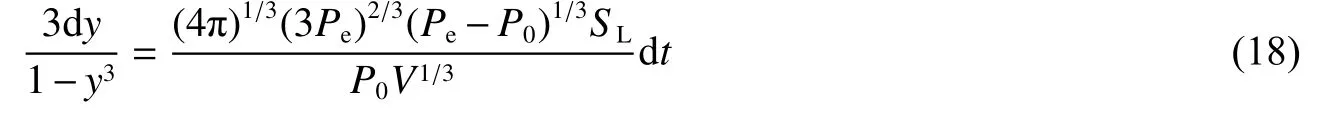
兩邊同時積分可得：

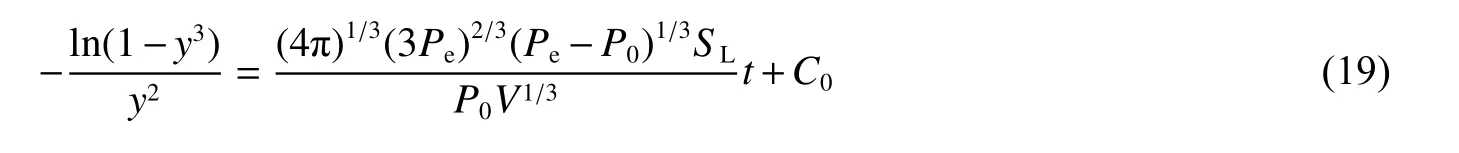
因此，可得：

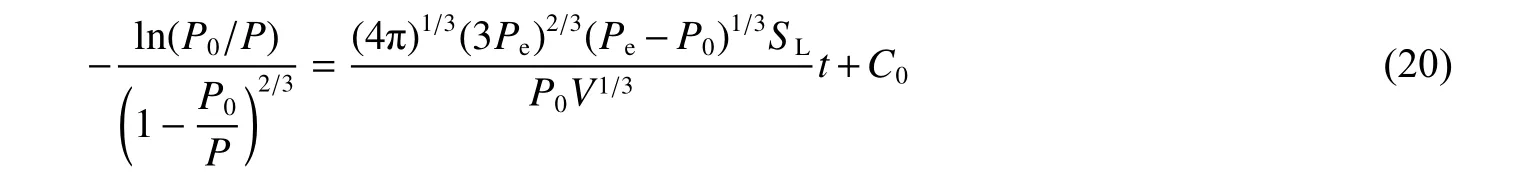
式（20）與文獻[12]所得結果形式相同。因此，在一定的壓力范圍以內，其近似解可表示為：

此時，球形密閉空間內爆炸超壓可表示為：

利用相關實驗對此模型進行對比驗證，其實驗條件如表1 所示：實驗1 和實驗2 所選用可燃預混氣體為甲烷/空氣預混氣體，實驗3 和實驗4 所選用氣體為氫氣/空氣預混氣體，但所有實驗所對應氣體的體積濃度均位于化學當量比附近。而就密閉空間體積而言，實驗1 和實驗3 所對應密閉空間體積較小，實驗2 和實驗4 所對應密閉空間體積大，但密閉空間形狀均為球形。針對上述實驗條件，將實驗所得可燃預混氣體爆炸超壓結果和利用式（22）計算所得爆炸超壓結果進行對比，如圖1～2 所示。

表 1 各實驗條件[15-17]Table 1 Experimental conditions

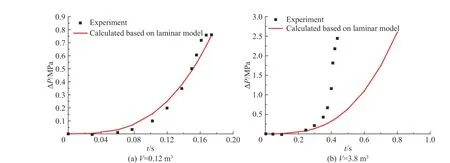
圖 1 甲烷/空氣預混氣體爆炸超壓時程曲線Fig. 1 Overpressure time history curve of CH4/air mixture gas explosion

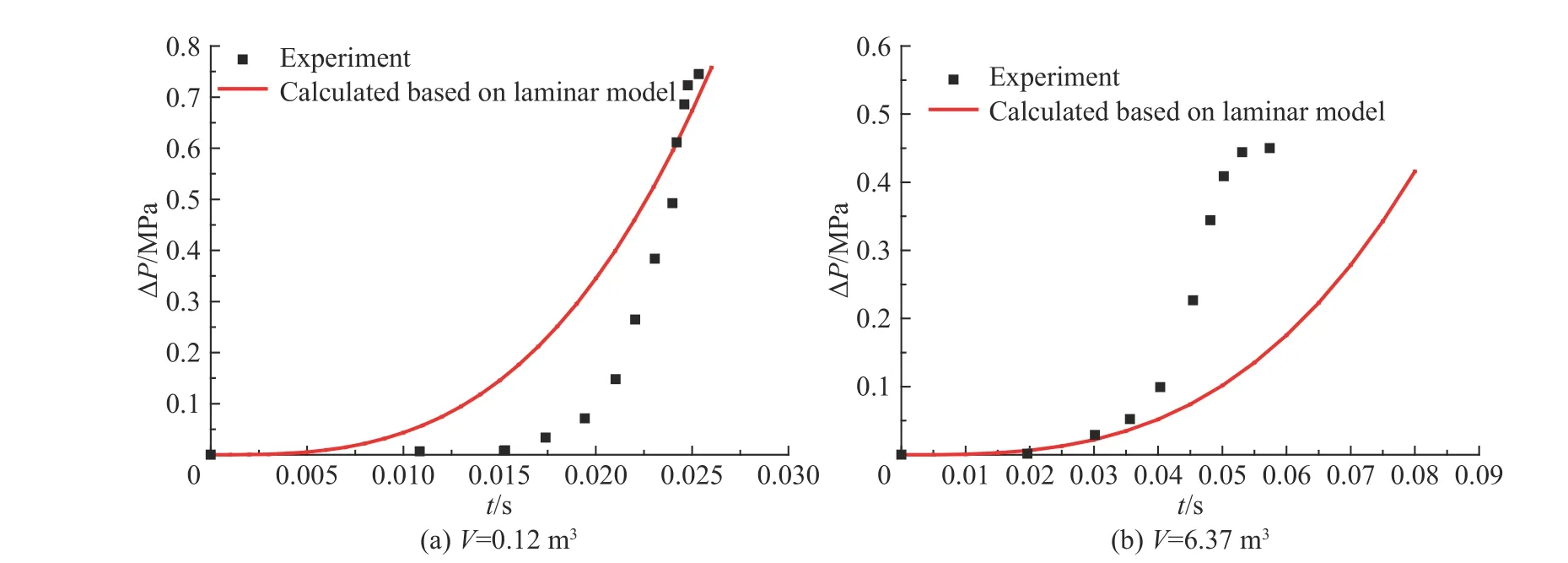
圖 2 氫氣/空氣預混氣體爆炸超壓時程曲線Fig. 2 Overpressure time history curve of H2/air mixture gas explosion

從圖1 可以看出：當密閉空間體積較小時，對甲烷/空氣可燃預混氣體而言，運用層流光滑火焰傳播理論計算所得爆炸超壓與實驗所得基本完全一致。從圖2 可以看出：當密閉空間體積較小時，對氫氣/空氣預混氣體而言，在爆炸初期，運用層流燃燒理論計算所得爆炸超壓相比實驗所得稍大一些；在爆炸后期，理論計算所得結果與實驗變化趨勢基本一致。因此，當密閉空間體積較小時，運用光滑層流火焰傳播理論建立的爆炸超壓預測模型與實驗結果基本相符。

然而當球形密閉空間體積較大時，針對實驗2 和實驗4 兩種情況預混可燃氣體，運用光滑層流火焰傳播理論計算所得爆炸超壓值均遠小于實驗所得，依據光滑層流火焰傳播理論所建立的爆炸超壓預測模型存在較大的誤差。其主要原因是密閉空間體積較大時，爆炸火焰從點火中心開始發展，隨著火焰半徑的不斷擴大，光滑層流火焰逐漸失穩，最終演變成褶皺甚至湍流火焰向外傳播。此時，火焰前鋒面會出現褶皺和裂紋[18]，導致球形火焰前鋒面表面積顯著增大和燃燒反應區增大，同時燃燒反應產生的熱更快地傳遞到未燃區域促使產生新的燃燒反應，進而使得單位時間內可燃預混氣體質量較光滑層流火焰時減少較多，導致爆炸超壓值明顯增大。

為了使計算模型能夠更好地在密閉空間結構抗爆設計和日常安全管理中得到應用，從圖中選取結構抗爆設計過程和日常安全管理過程中的重要參數之一—可燃預混氣體爆炸時的峰值超壓[19]，并對其進行進一步分析，結果如表2 所示。

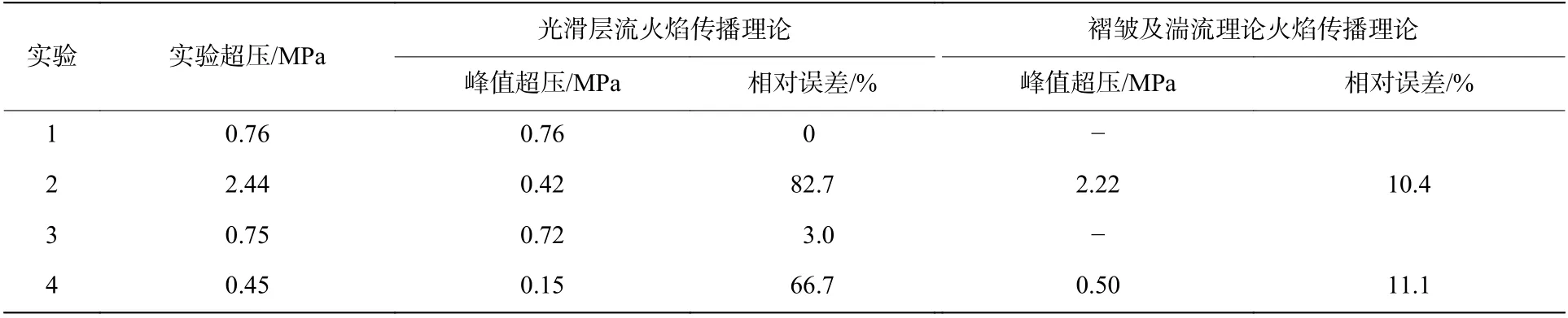
表 2 實驗與理論計算峰值超壓值Table 2 Peak overpressure of experimental and theoretical calculations

通過對比發現，當密閉空間體積為0.12 m3時，對于甲烷/空氣可燃預混氣體，理論計算所得峰值超壓與實驗值完全一致；對于氫氣/空氣可燃預混氣體，理論計算所得峰值超壓與實驗所得相對誤差為3.0%，而在整個爆炸過程中，理論計算所得結果與實驗所得變化趨勢基本一致，此時所產生的誤差為系統誤差[20]。因此，當密閉空間體積較小時，利用光滑層流火焰傳播理論計算所得峰值超壓可用于工程結構抗爆設計和日常安全管理。

然而，當密閉空間體積為3.80 和6.37 m3時，所對應甲烷/空氣可燃預混氣體和氫氣/空氣可燃預混氣體，理論計算所得峰值超壓與實驗所得相對誤差分別為82.7%和66.7%，所產生的誤差較大。此時利用光滑層流火焰傳播理論計算所得峰值超壓來進行結構抗爆設計時，將嚴重低估可燃預混氣體爆炸時的爆炸威力，使得所設計結構無法抵抗氣體爆炸時所產生的超壓，從而導致嚴重的安全事故。因此，當密閉空間較大時，利用光滑層流火焰傳播理論所得峰值超壓不能用于工程結構抗爆設計和日常安全管理。

2 褶皺及湍流火焰傳播爆炸超壓預測

2.1 褶皺及湍流火焰形成及特征

爆炸火焰在燃燒過程中主要受流體動力學不穩定性和熱擴散不穩定性影響。流體動力學不穩定性主要由火焰兩側的密度差所造成，因此在整個爆炸火焰傳播過程中自始至終一直存在；熱擴散不穩定性主要由火焰內部熱擴散和質量擴散不均衡引起[21-23]。流體動力學不穩定性和熱擴散不穩定性兩者共同作用使得球形爆炸火焰在傳播過程中被劃分為光滑階段、轉捩階段和飽和階段[24]，如圖3 所示，圖中R 表示球形密閉空間半徑，r 表示火焰半徑，r0表示臨界火焰半徑。

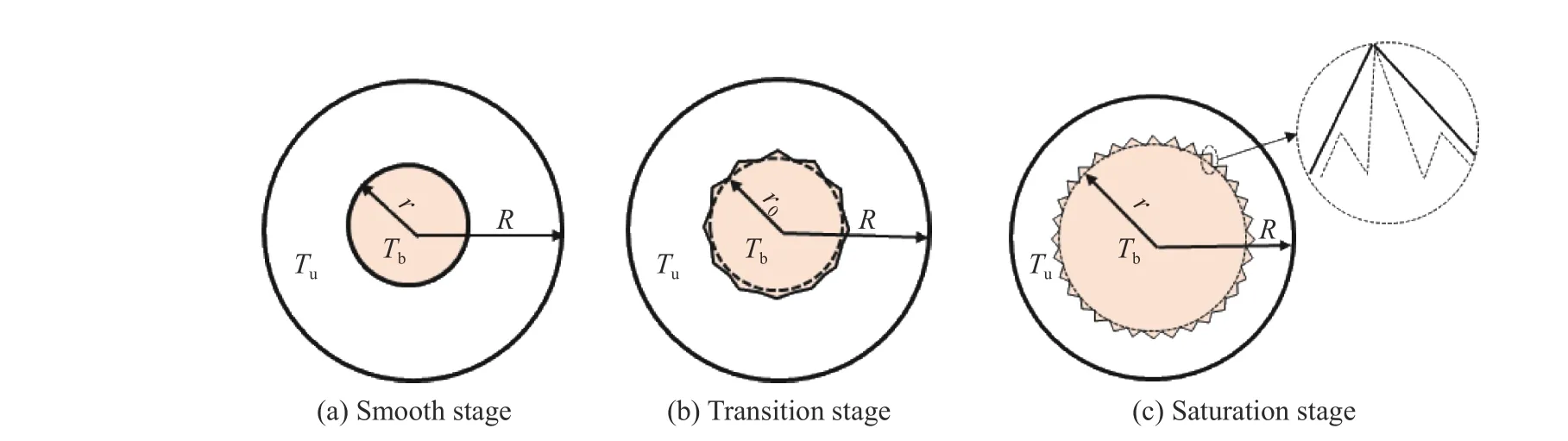
圖 3 爆炸火焰傳播Fig. 3 Diagram of explosion flame propagation

密閉空間中心點火后，在光滑階段，火焰前鋒面較為光滑，以較為穩定的燃燒為主。受熱擴散不穩定性影響，當火焰前鋒面到達臨界火焰半徑時，火焰前鋒面產生分裂線，也就是火焰產生失穩變形而發生褶皺，此時火焰傳播特征發生轉捩[25]。

隨后，隨著火焰前鋒面的進一步傳播，熱擴散不穩定性相比流體動力學不穩定性越來減弱，流體動力學不穩定性越來越明顯，尤其是在實驗2 和實驗4 條件下，可燃預混氣體體積分數接近化學當量比，此時燃燒速度最快，流體動力學不穩定性最強。在流體動力學不穩定性作用下火焰前鋒面出現交叉裂紋，交叉裂紋不斷分裂形成細小的裂紋，直至形成較為均勻的完全胞狀，即達到飽和階段。與此同時，火焰傳播速度迅速增加，且當密閉空間體積較大時，火焰將變成湍流火焰，火焰前鋒面不再是光滑層流燃燒中的球形火焰前鋒面，而是隨著火焰前鋒面的向外傳播表現出近似于球形的不規則形狀[26]。

針對上述火焰傳播過程中所形成的褶皺及湍流火焰，相關研究表明[27-29]：其火焰前鋒面具有典型的分形特征，在流場中存在著尺寸連續變化的渦團，在幾何特征與運動規律方面都是相似的，只是尺度不同而已，他們共同組成明顯的自相似圖形族。不同尺度的渦團圖形在同一時刻相互重疊，表面上形成混沌和無序，但本質上卻包含著有序性。因此，褶皺及湍流爆炸火焰在傳播過程中表現出自相似性。

2.2 爆炸超壓建模及結果分析

受限空間預混可燃氣體爆炸火焰傳播過程中，基于上述分析，可用分形燃燒模型來進行分析，假設褶皺及湍流預混火焰傳播時預混火焰前鋒面可以被視為一個無限薄的面，將已燃區和未燃區完全分開，且所有的燃燒都在火焰前鋒面上進行，此時褶皺火焰前鋒面表面積大大增加，使得燃燒速度加快。基于此，褶皺及湍流火焰傳播速度采用火焰面分形理論來進行計算，湍流火焰傳播速度ST與拉伸的層流火焰傳播速度之間存在如下關系[25]：

分形主要從幾何角度為湍流燃燒的有序特性提供了依據，Gouldin 第一個提出將分形應用于預混燃燒，建立了修正湍流火焰速度的預測模型，在分析過程中認為湍流火焰的分形維數應介于2.35～2.41 之間[33]；Kerstein 從動力學角度分析證明湍流預混火焰在充分發展時分形維數為7/3[34]；Liberman 利用數值模擬得出球形火焰褶皺時的分形維數在2.4 左右[35]；Yoshida 等研究發現預混火焰隨其湍流強度的增大分形維數在2.17～2.32 之間變化，最終趨于2.36[36]。因此，本文中取D3=2.36。

對于較大體積密閉空間，基于上述分析和式（23），可燃預混氣體爆炸火焰傳播過程中，火焰傳播速度如圖4 所示。

從圖4 可以看出：在密閉空間內，對于甲烷/空氣可燃預混氣體而言，在火焰前鋒面傳播至臨界火焰半徑0.08 m 之前，火焰鋒面保持恒定燃燒速度0.35 m/s 向四周自由膨脹；到達臨界火焰半徑轉捩之后，火焰傳播速度急劇增加至0.81 m/s；隨后火焰傳播速度以指數形式不斷增加，對其進行數據擬合，則火焰傳播速度隨時間的變化可表示為ST=0.73e0.5848t(R2=0.999 7)。對于氫氣/空氣可燃預混氣體而言，在火焰前鋒面傳播至臨界火焰半徑0.07 m 之前，火焰前鋒面保持恒定燃燒速度4.34 m/s 向四周自由膨脹；到達臨界火焰半徑轉捩之后，火焰前鋒面傳播速度急劇增加至8.6 m/s；隨后火焰前鋒面傳播速度與甲烷/空氣預混火焰傳播速度表現形式一致，也呈指數形式增加，其火焰傳播速度隨時間的變化可表示為ST=8.678 9e0.5086t(R2=1)。因此，對于上述兩種條件下的預混氣體火焰前鋒面傳播速度與時間之間的變化關系與文獻[31]所得規律基本一致。

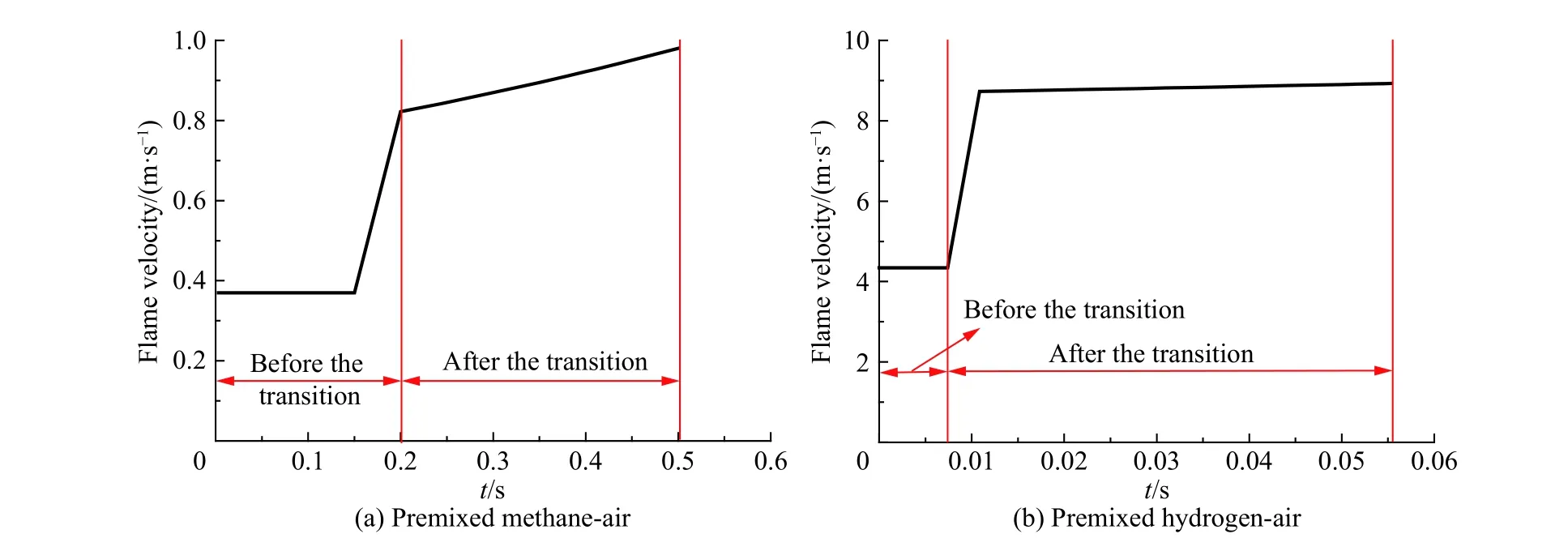
圖 4 火焰傳播速度時程曲線Fig. 4 Flame propagation velocity time history curves

基于火焰傳播過程中的火焰不穩定性和火焰形變，對造成上述結果的原因進行分析。在密閉空間內，爆炸火焰傳播初期，火焰不穩定性和火焰形變作用對火焰傳播速度的影響很弱，當火焰傳播至臨界火焰半徑之后，火焰不穩定性擾動形成褶皺，火焰由球形變換為滿足自相似分形的近似于球形不規則形狀，導致火焰前鋒面表面積呈指數形式增加，同時火焰不穩定也隨之增加，兩者共同作用使得火焰前鋒面傳播速度顯著增加[37]。因此，在火焰傳播的后期，火焰不穩定性和火焰形變對火焰傳播速度的影響非常大，對火焰速度的增加具有非常大的貢獻。

此時，對比層流火焰傳播時的式（4），湍流燃燒條件下單位時間內可燃氣體質量變化率可表示為：

定義褶皺及湍流火焰傳播速度ST與無拉伸時光滑層流火焰傳播速度SL之比為湍流因子 α ，則有如下關系式：

將式（25）代入式（21），類比前面層流火焰傳播時爆炸超壓的推導過程，可得湍流火焰傳播時爆炸壓力近似為：

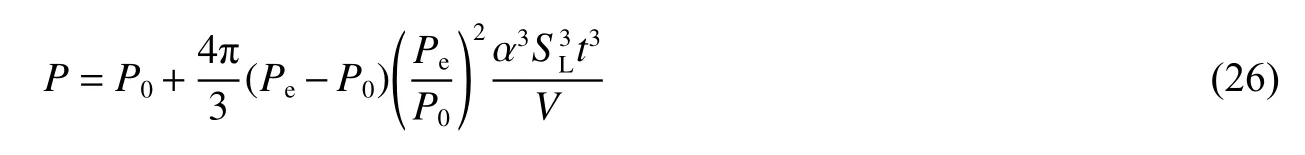
此時，球形密閉空間內爆炸超壓為：

在火焰傳播過程中，當瞬時火焰鋒面當量球半徑超過臨界火焰半徑時，火焰前鋒面發生褶皺并最終發展成為湍流火焰。基于此，利用式（27）對實驗2 和實驗4 條件下的爆炸超壓進行計算，并與實驗所得結果進行對比，理論值與實驗值所對應結果如圖5～6 所示。

從圖5 可以看出：甲烷/空氣預混氣體所處密閉空間體積較大時，基于褶皺及湍流火焰傳播理論計算所得爆炸超壓值與實驗所得結果有較好的一致性。從圖6 可以看出：氫氣/空氣預混氣體所處密閉空間體積較大時，基于褶皺及湍流火焰傳播計算所得爆炸超壓值與實驗所得也有較好的一致性。驗證了依據褶皺及湍流火焰傳播所建立爆炸超壓模型的可靠性，因為在褶皺及湍流火焰傳播時，火焰傳播過程發生了燃燒失穩，形成不同尺度的渦團，且在同一時刻相互重疊，表面上形成混沌和無序，使得未燃物和可燃物之間的傳熱和傳質較光滑層流火焰劇烈很多。同時褶皺及湍流火焰傳播時，火焰前鋒面褶皺后，火焰前鋒面被拉伸，單位時間內流入火焰前鋒面的未燃混合物明顯增多。兩者共同作用，使得褶皺及湍流燃燒火焰傳播速度較光滑層流大很多。

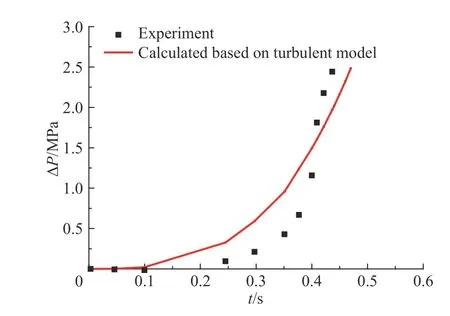
圖 5 甲烷/空氣混合氣體爆炸超壓時程曲線（V=3.8 m3）Fig. 5 Overpressure of CH4/air mixture gas explosion

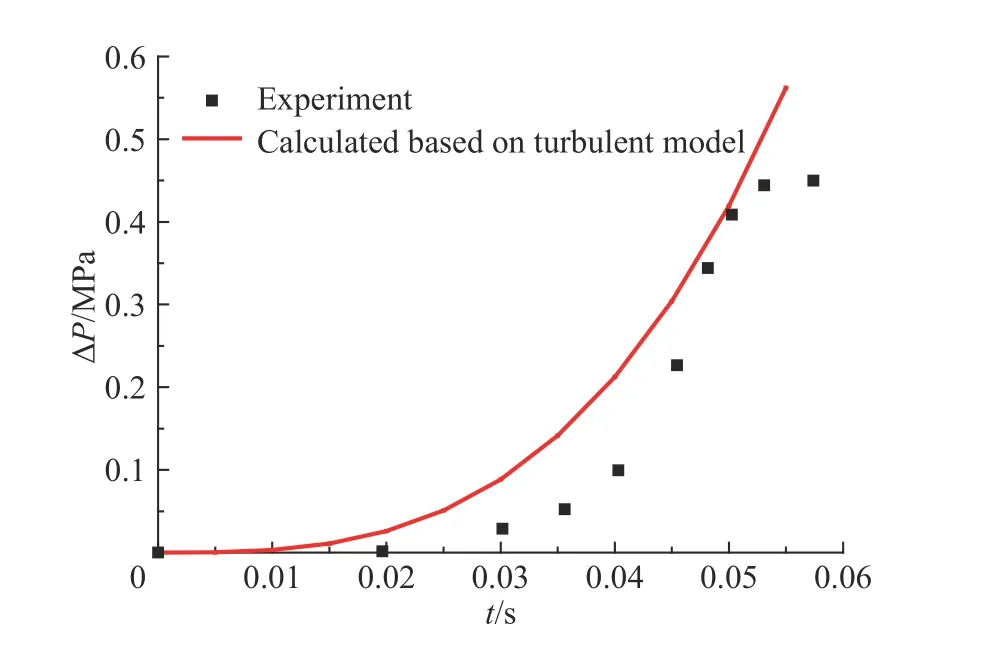
圖 6 氫氣/空氣混合氣體爆炸超壓時程曲線（V=6.7 m3）Fig. 6 Overpressure of H2/air mixture gas explosion

但就兩種條件下的預混可燃氣體相比較而言，氫氣/空氣預混氣體爆炸時火焰傳播速度較甲烷/空氣預混氣體爆炸時火焰傳播速度大很多，同時氫氣/空氣預混氣體所處受限空間體積較甲烷/空氣預混氣體所處受限空間體積大很多。因此，在爆炸火焰傳播過程中，當爆炸火焰以湍流形式傳播時，所表現出自相似分形特性更為明顯。而在爆炸火焰傳播初期，兩種條件下計算所得結果均大于實驗所得，其主要原因是由于理論計算過程中均假設密閉空間壁面與外界無任何能量交換，且未考慮可燃預混氣體點火時存在延遲。在爆炸火焰傳播后期，實驗2 所對應條件下計算所得爆炸超壓略小于實驗所得，其主要原因是由于在理論模型在計算過程中忽略了壓力升高對爆炸火焰傳播速度的影響，在真實的爆炸火焰傳播過程中，隨著壓力的升高，爆炸火焰傳播速度會進一步加快。

同時，選取爆炸過程中的峰值超壓進行分析，結合表2 可以看出：當密閉空間體積分別為3.80 和6.37 m3時，利用褶皺及湍流火焰傳播理論建立的爆炸超壓預測模型進行峰值壓力計算時，兩種工況下實驗所得和理論計算所得相對誤差分別為10.4%和11.1%。通過前段所述理論與實驗誤差的分析，可判定該誤差也為系統誤差[20]。此時，與利用光滑層流火焰傳播理論所建立模型計算所得誤差相比，所對應的誤差分別減少了72.3%和50.6%，極大地提高了較大密閉空間爆炸超壓預測模型的可靠度。因此，所建立模型在一定程度上可為密閉空間抗爆設計和日常安全管理提供支持。

3 結果分析

密閉空間在中心點火后，在不同空間體積條件下，受熱擴散不穩定性和流體動力學不穩定性影響，火焰傳播表現出不同的形態。當密閉空間體積較小時，火焰傳播時間較短，火焰前鋒面不穩定性主要受熱擴散不穩定性影響，火焰前鋒面基本保持光滑且以層流為主進行傳播；當密閉空間體積較大時，受熱擴散不穩定性和流體動力學不穩定性兩者共同作用，在一定條件下，光滑火焰傳播階段主要受熱擴散不穩定性影響，在轉捩階段和飽和階段主要受流體動力學不穩定性影響，使得火焰傳播由光滑層流火焰逐漸轉變為具有自相似分形特征的湍流火焰。

因此，針對不同密閉空間體積情況：當體積較小時，利用光滑層流火焰傳播理論所建立的爆炸超壓預測模型能較好地對其可燃預混氣體爆炸超壓進行預測。但當密閉空間體積較大時，計算所得誤差較大，此時以褶皺及湍流自相似分形火焰傳播理論為依據，考慮褶皺及湍流因子，可建立褶皺及湍流火焰爆炸超壓預測模型。

綜合光滑層流火焰傳播和褶皺及湍流火焰傳播兩種情況，對密閉空間內可燃預混氣體爆炸時的爆炸超壓進行歸一化表示。在一定的誤差范圍內，可得密閉空間內可燃預混氣體爆炸時的爆炸超壓預測模型：

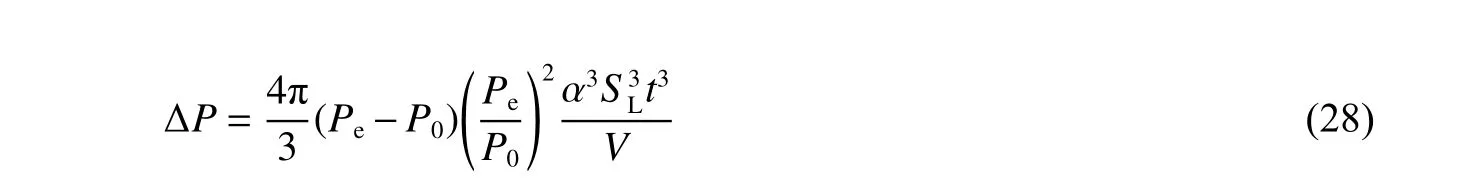
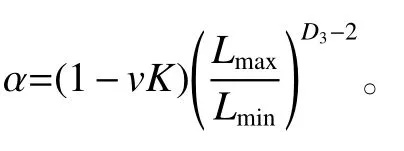
利用該模型能較好地對密閉空間內可燃預混氣體爆炸超壓進行預測。

4 結 論

（1）針對不同體積的密閉空間，在分析不同體積條件下爆炸時可燃預混氣體火焰傳播過程的基礎上，運用光滑層流火焰傳播理論和褶皺及湍流火焰傳播時滿足分形特征的特點，建立了不同體積條件下的爆炸超壓預測模型，該模型能較好地預測球形密閉空間可燃預混氣體爆炸時的爆炸超壓。

（2）本文中褶皺及湍流火焰傳播過程中臨界火焰半徑是以實驗為基礎確定的，對于分形維數等參數的確定選用了前人研究所得的結果。然而，實際密閉空間爆炸時，褶皺及湍流火焰傳播過程中不同的湍流強度及火焰傳播速度對分形維數也會造成不同的影響。

（3）本文為前瞻性研究，就密閉空間可燃氣體爆炸超壓模型而言，還存在很大的研究潛力，后續可基于本文研究方法，對不同空間、不同點火位置、不同氣體、不同條件下的爆炸火焰傳播過程不穩定性進行研究。在研究過程中可借助先進的實驗條件、理論分析和數值模擬等手段對其進行深入的分析，以得到更為全面的密閉空間可燃氣體爆炸超壓預測模型。