一種方法破解十三種變形

■河北省南宮市教育局教研室

■河北省南宮中學 霍忠林

賦值法是二項式定理的一個重要應用,它體現的是一種從一般到特殊的轉化思想。用賦值法處理二項式展開式中與項的系數相關的問題,一直以來都是各地高考及模擬考試的熱點問題。本文從一道例題出發,通過十三個由淺入深的變式,將賦值法常見的各種題型一一歸納總結,以期對同學們提供幫助。

例題若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a0+a1+…+a7的值。

解析：令x=1,則a0+a1+…+a7=27。

變式1若(3x-1)7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a0+a1+…+a7的值。

解析：令x=2,則a0+a1+…+a7=57。

變式2若(3x-1)7=a0+a1(2x-1)+a2(2x-1)2+…+a7(2x-1)7,求a0+a1+…+a7的值。

解析：令x=1,則a0+a1+…+a7=27。

評析：運用賦值法在解決形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a0+a1+…+an的值”問題時,只需令sx+t=1,即將帶入等式左邊,從而得到所求結果

變式3求(3x-1)7的展開式中所有項的系數和。

解析：該變式與變式1相同,只是形式上沒有變式1更“直觀”,答案略。

變式4求(2x+1)(3x-1)7的展開式中所有項的系數和。

解析：令x=1,則展開式中所有項的系數和為3·27。

變式5求(2x+y)(3x-y)7的展開式中所有項的系數和。

解析：令x=y=1,則展開式中所有項的系數和為3·27。

評析：運用賦值法在解決形如“求(ax+by)n(cx+dy)m(其中a,b,c,d為常數)展開式中所有項的系數和”問題時,只需將兩變量x=1,y=1代入等式左邊,從而得到所求結果(a+b)n(c+d)m。

變式6若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a0-a1+a2-a3+…+a6-a7的值。

解析：令x=-1,則a0-a1+a2-a3+…+a6-a7=(-4)7。

評析：運用賦值法在解決形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a0-a1+a2-…+(-1)nan的值”問題時,只需令sx+t=-1,即將代入等式左邊,從而得到所求結果

變式7若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a1+a3+a5+a7和a0+a2+a4+a6的值。

解析：注意到a0+a1+…+a7=27,a0-a1+a2-a3+…+a6-a7=(-4)7。

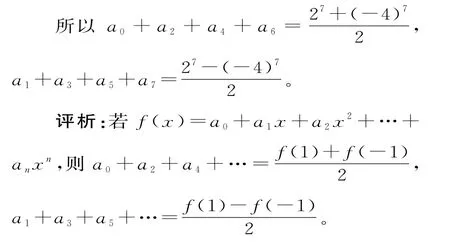
變式8若(3x-1)7=a0+a1x+a2x2+…+a7x7,求|a0|+|a1|+…+|a7|的值。

解析：注意到a0,a2,a4,a6均為負數,a1,a3,a5,a7均為正數,所以：

|a0|+|a1|+…+|a7|

=-a0+a1-a2+a3-a4+a5-a6+a7

=-(a0-a1+a2-a3+a4-a5+a6-a7)=-(-4)7=47。

評析：對比(3x-1)7和(3x+1)7展開式中次數相同項的系數,易發現變式8中|a0|+|a1|+…+|a7|的值就等于(3x+1)7展開式中各項的系數之和,因此在運用賦值法解決形如“(ax+b)n=a0+a1x+a2x2+…+anxn,求|a0|+|a1|+…+|an|的值”的問題,就可以轉變為“求（|a|x+|b|）n展開式中各項的系數之和”問題來處理。

變式9若x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a0+a1+…+a7的值。

解析：解法一,令x=2,則a0+a1+…+a7=27。

解法二,令t=x-1,則(t+1)7=a0+a1t+a2t2+…+a7t7。再令t=1,則a0+a1+…+a7=27。

評析：解法二通過換元將問題轉化為同學們熟知的問題,這種處理尤其在求特定項的系數時(比如本題中若求a2的值),非常便利。

變式10若x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a1+2a2+3a3+…+7a7的值。

解析：x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,兩邊分別對x求導得：

7x6=a1+2a2(x-1)+3a3(x-1)2+…+7a7(x-1)6。

令x=2,得a1+2a2+3a3+…+7a7=7·26。

評析：運用賦值法在解決形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a1s+2a2s+3a3s+…+nans的值”問題時,可將等式兩邊分別先對x求導,再賦值來處理。當a=1,b=0,s=1,t=-1,n=7,就是變式10。特別地,有時候需要對等式兩邊多次求導,再賦值,比如變式11。

變式11若(3x-1)7=a0+a1x+a2x2+…+a7x7,求2a2+6a3+12a4+20a5+30a6+42a7的值。

解析：(3x-1)7=a0+a1x+a2x2+…+a7x7,兩邊分別對x求導得：

21(3x-1)6=a1+2a2x+3a3x2+4a4x3+5a5x4+6a6x5+7a7x6。

兩邊再對x求導得：

378(3x-1)5=2a2+6a3x+12a4x2+20a5x3+30a6x4+42a7x5。

令x=1,得2a2+6a3+12a4+20a5+30a6+42a7=378·25。

變式12若(3x-1)7=a0+a1x+a2x2+…+a7x7,求的值。

解析：令

評析：由于待求式子中各分母的次數與對應分子中下標的數字相同,因此可以直接進行賦值即可。

變式13若(3x-1)7=a0+a1x+a2x2+…+a7x7,求的值。

解析：兩邊各自在區間[0,t]上求積分,得

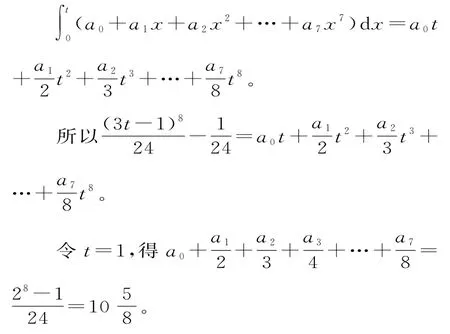
評析：注意本題與變式12的區別,本題中分母數字比對應的分子次數多1,容易想到公式因此可以借助于定積分來處理。

總之,運用賦值法處理二項式展開式中與系數和有關的問題時,要注意觀察所求式子的結構特征,靈活“賦值”,才能順利解決問題。這種解決問題的能力,需要同學們自己“琢磨—總結—內化—應用”,只有這樣才能不斷地提高大家的學科素養。