灰色關聯分析與模糊推理邊緣檢測圖像融合法

張洪群，顧吟雪，2，郭擎

(1.中國科學院空天信息創新研究院，北京 100094；2.南京大學金陵學院 城市與土木工程院系，南京 210000)

0 引言

隨著遙感技術的逐漸進步，如何提取并綜合利用不同類型圖像的信息已成為遙感的重要問題[1]。遙感圖像融合把傳感器采集到的同一地物的多光譜圖像(multispectral image，MS)和全色圖像(panchromatic image，PAN)經過計算機技術的處理，提取MS中的光譜信息和PAN中的空間細節信息，最后綜合成同時具有高空間分辨率和高光譜分辨率的融合圖像。與單一遙感圖像相比，融合后的圖像既可以增強圖像的細節信息，又可以保持原始光譜信息，以提高圖像利用率。

遙感圖像融合算法主要分為兩大類，一類是成分替換法(component substitution，CS)，另一類是多分辨率分析方法(multiresolution analysis，MRA)[2]，當然還有一些混合法，以及最近幾年出現的稀疏表達法和變分法[3-4]。CS類融合法由于計算簡單而被廣泛應用，如Brovey[5]、PCA (principal component analysis)[6]、IHS (intensity-hue-saturation)[7-8]和GS (gram-schmidt)[9]，其中又以IHS算法更為突出。不過，IHS算法容易產生光譜失真，因為含有部分光譜信息的亮度分量被整個全色圖像替換掉了。針對IHS算法的局限性，伍娟等[10]提出了基于IHS變換與直方圖匹配的圖像融合方法，實驗表明，該融合方法能夠保持融合前圖像的光譜特征和空間特征同時存在。但是由于IHS算法是把亮度分量直接進行替換，圖像中的光譜扭曲程度仍然小范圍存在，因此，為了得到更好的融合圖像，學者們開始把IHS算法與其他算法結合起來。其中，肖化超等[11]提出了基于IHS變換和Curvelet變換的衛星遙感圖像融合方法，保留了光譜信息，能有效提高圖像的空間分辨率；田云翔等[12]將魯棒主成分分析與IHS變換相結合，有效提高了圖像融合的質量；Sojasi S等將IHS方法和HPM (high-pass modulation)方法相結合進行圖像融合，有效提高空間分辨率和保持光譜信息。

圖像融合算法中如何在提高空間分辨率的同時保持多光譜圖像的光譜信息一直是一個難點，而且由于成像傳感器的差異和各種干擾的存在，融合后的圖像會產生不同等級程度的失真和噪聲問題。為解決這些問題，本文在IHS算法的基礎上，提出一種結合灰色關聯分析、模糊推理和IHS變換的圖像融合算法。該算法主要分為兩部分，一部分是邊緣檢測，另一部分是圖像融合。邊緣檢測方面，通過灰色關聯分析和模糊推理的結合，選擇出最有可能是邊緣的點加以保留，該方法能檢測出圖像豐富的邊緣信息，提高融合后圖像的空間分辨率；圖像融合方面，基于加權融合的規則把真正的邊緣細節信息和IHS變換相結合，僅把多光譜圖像所缺少的全色圖像中的空間細節信息融進來，而不是整個的替換，能夠很好地對互補信息和冗余信息進行較為合理的融合，減少光譜失真。將本文方法與IHS算法、Brovey算法、PCA算法、MTF_GLP_HPM(modulation transfer function-generalized laplacian pyramid，HPM)算法[13]和GS算法作對比實驗。結果表明，本文提出的算法在邊緣檢測的基礎上解決了IHS算法帶來的光譜失真問題，使圖像同時保持了空間分辨率和光譜分辨率。

1 圖像融合方法

本文以邊緣檢測為基礎，聯合灰色關聯分析和模糊推理算法對全色圖像的邊緣進行提取，得到盡量豐富、真實的空間細節信息邊緣，從而對IHS融合法進行改進。基于該邊緣信息，把I分量和直方圖匹配后的全色圖像進行加權融合，把多光譜圖像所缺少的空間細節信息融合進來，使融合結果在較優保持光譜信息不變的基礎上，盡可能地融入全色圖像的細節信息，融合后的圖像局部特征表征能力突出，細節信息清晰。

1.1 灰色關聯分析算法

灰色關聯分析是灰色系統重要的組成部分[14]，是一種較好的圖像邊緣檢測方法[15-16]。其基本方式是通過對比參考數列和比較數列的幾何形態的相似程度來計算參考數列和比較數列的關聯程度。若兩條曲線相似程度高，則關聯度大，反之則關聯度低。

邊緣是圖像中灰度值發生顯著變化的一組像素。理想的非邊緣點是某點像素值和周圍的像素值相同。因此，將一個像素和其相鄰像素形成一個參考數列，使其取相同的值，則該點元素為非邊緣點。本文采用一個值為1的5點序列(即該像素及其上、下、左、右相鄰元素)作為參考序列；比較數列由每個像素及其相應的4個相鄰的像素組成。那么對于M×N大小的圖像，步驟如下：

①確定參考數列和比較數列。

參考數列：Xc(k){1，1，1，1，1}

比較數列：Xb(k){Xi-1，j，Xi，j-1，Xi，j，Xi，j+1，Xi+1，j}

i=1，2，3，…，M；j=1，2，3，…，N

其中，當i，j=0，或i=M，j=N，把相鄰行或列上對應位置的像素值重復，使其作為該點的值。

②計算以各像素點為中心形成的比較數列與參考數列之間的灰色關聯系數ξr。

(1)

其中

Δmin=min|Xc(k)-Xb(k)|

Δmax=max|Xc(k)-Xb(k)|

Δr(k)=|Xc(k)-Xb(k)|

r=1，2，3，…，M×N；k=1，2，…，5

式中：ξ為分辨系數，一般取0.5，保證ξr(k)∈(0，1]；Δmin和Δmax分別為Xc(k)數列與Xb(k)數列的最小絕對差值和最大絕對差值；Δr(k)為Xb(k)與Xb(k)的絕對差值。

③計算以各像素點為中心形成的參考數列與比較數列之間的灰色關聯度Rr。

(2)

邊緣點的判斷規則：當Rr大于某一設定的關聯度閾值θ時，說明該像素點與參考數列具有相似的特性，是非邊緣點，否則是邊緣點。關聯度閾值θ取值越大，邊緣信息越豐富；閾值θ取值越小，則反之。

1.2 模糊推理

模糊推理作為近似推理的一個分支，其步驟為：首先將原始圖像進行模糊化處理，轉換成給定范圍內的模糊集合，構造出正確的隸屬度函數；再在規則庫中選擇對應的模糊規則和合適的模糊推理方法，獲到推理結果；最終對推理結果進行去模糊處理，得到期望的圖像，能夠有效地檢測復雜結構的邊緣[17-19]。

隸屬度函數作為模糊推理中的重要一環，是否正確地構造隸屬度函數是能否用好模糊推理的關鍵之一。輸入輸出對應的隸屬度函數，如圖1所示，模糊推理規則如表1所示。本文定義模糊集合對應的語言變量為黑和白，其中黑表示輸入隸屬度與圖像灰度值呈負相關，白表示輸入隸屬度與圖像灰度值呈正相關，輸入隸屬度的值越靠近1，相關性越高；越靠近0，相關性越低，如圖1(a)所示。輸入隸屬度函數采用梯形函數，梯形隸屬度函數具有很強的抗干擾能力，使檢測出的邊緣更加清晰，如式(3)所示。

圖1 輸入輸出對應的隸屬度函數

表1 模糊推理規則

定義模糊集的輸出語言變量為黑、白和邊緣。利用三角形隸屬函數分離出圖像邊緣部分，通過公式(4)至公式(6)計算得出黑、白、邊緣的準確值。

(3)

模糊推理方法運用Mamdani算法，利用最小型運算規則定義模糊包含表達的模糊關系，比如規則R：

x：輸入語言變量

y：輸出語言變量

A：推理前的模糊集合

B：模糊后的模糊集合

其模糊關系Rc定義：

(4)

式中：μA(x)、μB(y)分別是A和B的隸屬度函數；μA(x)∧μB(y)表示在μA(x)、μB(y)中取較大者；X，Y是x，y的論域集合。當x為A*(A*為論域X上的模糊集合)，且模糊關系的合成運算運用最大最小運算時，模糊推理的結果如下：

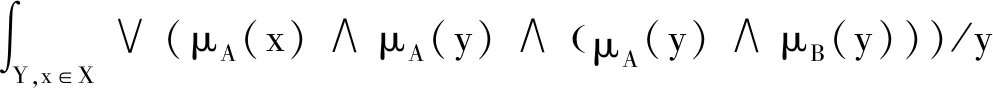
(5)

式中：μA(x)∧μB(y)表示在μA(x)、μB(y)中取較小者。

相位調制處理后，根據存儲的子信號相位，能夠對信號采樣時間進行選擇。對所選子信號進行實時采樣，就得到了與脈壓雷達信號波形完全相同的相位調制子脈沖串。

每條規則由 Mamdani 型模糊推理系統推理后，輸出的是變量隸屬函數的模糊集合。利用公式(6)計算出分割明顯的圖像灰度為黑、白和邊緣的合集y*：

(6)

本文以某一像素點周圍像素點的情況來檢測邊緣點。主要的推理規則是計算出每個像素點相鄰的8個像素點的灰度值，以3×3 模板為標準的推理規則推理出分割清晰的黑點、邊緣點和白點。

1.3 圖像融合步驟

圖像融合步驟如下：

①利用灰色關聯分析和模糊推理算法對PAN圖像的邊緣進行提取，將邊緣區域和非邊緣區域分開，得到邊緣區域像素值為1，非邊緣區域像素值為0的邊緣二值圖像E。

②對MS圖像進行IHS變換，得到亮度(I)分量、色度(H)分量和飽和度(S)分量。

③把原始PAN圖像與MS圖像的亮度(I)分量作直方圖匹配，得到直方圖匹配后的全色圖像PANh。

④依據邊緣圖像E的邊緣和非邊緣特征分布情況，對PANh圖像與MS圖像亮度(I)分量進行線性加權融合。為了使PAN圖像的細節信息更加明顯，賦予邊緣點較大權重，非邊緣點較小權重，從而得到新的亮度分量I′，如公式(7)：

I′[i，j]=w1×PANh[i，j]+w2×I[i，j]

(7)

⑤為了高度保持MS中的光譜信息，把PAN圖像和新的I′分量相乘再除以經過均值濾波的PAN圖像，得到最終的亮度分量I″。

⑥用最終的亮度分量I″和色度(H)分量和飽和度(S)分量進行IHS逆變換，得到最終的融合圖像。融合步驟的流程圖如圖2所示。

圖2 圖像融合流程圖

2 實驗結果和分析

為了驗證算法性能，本文采用的是經過幾何精校正、圖像配準等預處理后的圖像。實驗數據分為3組。算法實現的編程語言是MATLAB 2016。本文選取了5種方法與本文方法做對比，分別是IHS算法、Brovey算法、MTF_GLP_HPM算法、PCA算法、GS算法。

2.1 數據介紹

為了驗證本文方法對不同圖像的適用性，本文分別進行3組實驗，包括同源、異源，大尺寸、小尺寸，高分辨率和中分辨率圖像等。3組實驗所用衛星圖像類型、分辨率、圖像尺寸大小及波段合成如表2所示。

表2 衛星參數和圖像參數

2.2 融合圖像質量評價函數

為了客觀評價圖像融合的結果，實驗結果評價采用需要參考圖像的降尺度評價和不需要參考圖像的全分辨率評價2套評價方案，其中，降尺度評價又分空間質量評價和光譜質量評價。

1)降尺度評價[20]。降尺度評價是將融合圖像降尺度后和MS圖像進行對比，其中分為光譜質量評價和空間質量評價。光譜質量評價中的相關系數CC和光譜扭曲程度是評價R、G、B單波段融合質量的函數，圖像質量指數Q、結構相似度函數SSIM和相對無量綱的全局誤差ERGAS是評價3波段總體融合質量的函數；空間質量評價包括標準差，用來檢測融合圖像的空間質量。

相關系數(CC)用來反映融合圖像和參考圖像之間的相關程度。評價結果值在-1～1之間，相關系數越接近1，二者的相關性就越大；相關系數越接近-1，則反之。

光譜扭曲程度(degree of distortion，DoD)直接反映了圖像的光譜失真情況。其評價結果值越大，光譜失真越嚴重。值越小，反之，理想值為0。

圖像質量指數(Q)是反映融合圖像質量的評價函數，其值范圍在-1～1內，最優值為1。

結構相似度(SSIM)是一種用來衡量2幅圖像結構相似度的新指標。若SSIM值為1，則說明2幅圖像相同。

相對無量綱的全局誤差(ERGAS)是一種用于檢測融合圖像和參考圖像之間的光譜扭曲程度的參數，其評價結果值越小，光譜扭曲程度越小，最優值為0。

標準差(SD)反映了灰度偏離灰度均值的離散趨勢。標準差越大，則灰度級分布越離散。標準差的評價值與參考圖像的越接近，評價結果越好；反之，則越差。

2)全分辨率評價(full resolution validation)[2]。降尺度評價通常以MS圖像做參考檢驗融合圖像的質量，但是全分辨率評價可以在不需要參考圖像的基礎上，確定融合圖像的空間和光譜畸變。常用的全分辨率評價指數QNR的公式為：

QNR=(1-Dλ)α(1-Ds)β

(8)

式中：α和β是權重；Dλ、Ds分別表示光譜畸變和空間畸變。QNR的值越接近1，空間和光譜畸變就越小，融合圖像的質量也就越高。當QNR的值趨近于1時，Dλ、Ds的值越趨近于0。

光譜扭曲Dλ的計算公式為：

(9)

空間扭曲Ds的計算公式：

(10)

式中：PLP是一個與MS圖像的大小相同的低分辨率PAN圖像；q通常被設置為1。

2.3 邊緣檢測實驗與分析

為了選取灰色關聯分析的關聯度閾值θ，本文對lena圖邊緣檢測進行了不同閾值的驗證，如圖3所示。閾值為0.92的圖像因閾值較低而造成邊緣丟失的情況；閾值為0.94的圖像能夠檢測出豐富的邊緣細節；閾值為0.96的圖像所得邊緣較“厚”，邊緣定位精度不高，含有大量虛假邊緣。實驗表明，不同的圖像，閾值的設定不完全相同，實際操作中要結合提取出的邊緣信息情況。不過會有一個經驗參考，就是理論上閾值越大邊緣信息越豐富，不同的圖像有個微調，以能真實反映圖像邊緣信息為目的。本文經過多次實驗比較，經驗參考的閾值θ最終設定為0.94。同時，本文選取了canny算法、灰色關聯算法與本文邊緣檢測算法作對比，進一步驗證了灰色關聯分析和模糊推理的邊緣檢測算法的效果，結果如圖4所示。

圖3 Lena圖像邊緣檢測結果

圖4 不同方法邊緣檢測結果對比

由圖4可以看出，基于灰色關聯分析和模糊推理的邊緣檢測方法最佳，提取出的邊緣最全。canny算子提取出的邊緣不齊全但是對提取的邊緣進行了細化，視覺效果更佳。基于灰色關聯分析法邊緣檢測與基于灰色關聯分析和模糊推理的邊緣檢測相似，但是在圖像的細節邊緣方面，本文邊緣檢測方法稍好，邊緣提取更齊全，邊緣細節更豐富。本文方法所需的是邊緣提取更齊全的方法，以便在后續過程中能夠更好地增強融合后圖像的空間細節信息。

2.4 融合圖像的實驗結果與分析

實驗一采用了QuickBird衛星圖像，把本文方法的融合圖像與5種方法作對比，經過不斷的實驗，邊緣點與亮度分量線性加權的w1，w2權重的設定分別為0.8，0.2。如果PAN[i，j]為邊緣點，則w1[i，j]=0.8，w2[i，j]=0.2；如果PAN[i，j]為非邊緣點，則w1[i，j]=0.2，w2[i，j]=0.8。結果如圖5所示，評價結果如表3所示。

圖5 實驗一QuickBird數據融合結果

表3 實驗一圖像質量評價結果

從圖5的目視角度看，IHS算法的融合圖像、Brovey算法的融合圖像、PCA 算法的融合圖像和GS算法的融合圖像都有不同程度的光譜失真，MTF_GLP_HPM算法的融合圖像和本文方法的融合圖像從視覺上的表現都令人滿意。從表3的降尺度評價中看出，本文所提出的算法與其他算法相比，在表現空間細節信息的參數，如SD上有較好的提升，表明本文算法有較強的空間細節信息增強能力。反映光譜保持程度的參數，即CC、DoD、ERGAS、SSIM和Q表現較為優異，說明本文算法融合圖像的光譜失真情況減輕了很多。從全分辨率評價中看出，在無參考圖像下，融合圖像的質量參數，即Ds、Dλ、QNR總體表現良好，表明本文算法的光譜和空間扭曲程度很小。

實驗二使用了WV2衛星圖像，把本文方法與5種方法作對比，結果如圖6所示，評價結果如表4所示。

圖6 實驗二WV2數據融合結果

從目視角度上看，除了IHS算法的融合圖像有較為明顯的光譜失真情況，其他算法的融合圖像皆有良好的目視效果。

從表4看出，在無參考圖像的全分辨率評價中，本文方法的表現沒有MTF_GLP_HPM算法表現好。MTF_GLP_HPM算法的Ds參數和Dλ參數最小，QNR參數最大，在無參考圖像的質量評價中表現最好，但在降尺度評價中都與本文方法相差較大。IHS算法、PCA算法和GS算法結構相似度和相關系數較小，光譜扭曲程度較大，說明上面3種算法的融合圖像和原始多光譜圖像的差異較大，保持光譜信息稍少，且空間細節信息表現力不足。與其他方法相比較，本文方法的相關系數和結構相似度最大，光譜扭曲程度最小，最大限度地保留了高分辨率圖像中的細節信息，且保留了較多的光譜信息。

實驗三使用了SPOT和TM衛星圖像，把本文方法與5種方法作對比，結果如圖7所示，評價結果如表5所示。

表4 實驗二圖像質量評價結果

從目視角度看，IHS算法、Brovey算法、PCA算法和GS算法的融合圖像光譜信息損失較大，MTF_GLP_HPM算法的融合圖像和本文方法的融合圖像保留了較多的光譜信息。

由表5可看出，PCA算法、GS算法的結構相似度和標準差表現優異，但光譜扭曲程度最大，相關系數最小，說明PCA算法和GS算法的融合圖像很好地保持了空間信息，但光譜保持的信息最少。MTF_GLP_HPM算法結構相似度雖有提高，但是光譜扭曲程度有小幅度下降。本文方法結構相似度保持良好，光譜扭曲程度和相關系數優異，很好地達到了圖像的融合目的——既保留了原多光譜圖像中的光譜信息，又引入了高分辨率圖像的空間信息。在全分辨率評價中可以看出，本文方法的QNR參數最好，Dλ參數稍偏高，但是整體表現優異。

圖7 實驗三SPOT和TM數據融合結果

表5 實驗三圖像質量評價結果

3 結束語

本文針對圖像融合會出現的光譜失真問題，提出一種結合灰色關聯分析、模糊推理和IHS變換的圖像融合算法。基于灰色關聯分析和模糊推理的邊緣檢測方法可以檢測出具有更加完整、豐富的邊緣信息。在圖像融合算法中，基于檢測出的邊緣信息，利用全色圖像與多光譜圖像亮度分量的線性加權有效地融入所需要的空間細節信息并有效地保持原始多光譜圖像的光譜信息，減少光譜失真。

同時，由于本文算法簡單，使其可以應用于需要實時處理的遙感圖像融合應用場合，也為進一步改進邊緣檢測和圖像分割等技術做出了貢獻，這對提高遙感圖像融合的質量有一定的指導意義。

本文融合算法對遙感數據進行融合還存在以下問題：灰色關聯分析和模糊推理如何更緊密地結合，關聯度閾值的最優選擇等。將來在解決上述問題的前提上，為了提高遙感圖像處理和信息提取的精度和可靠性，融合圖像可以應用于分類、信息提取等后續處理中。