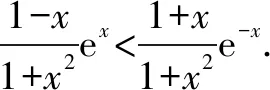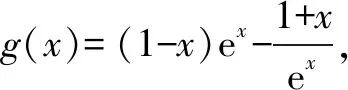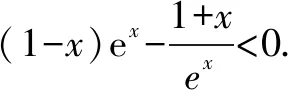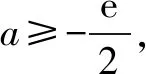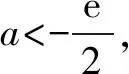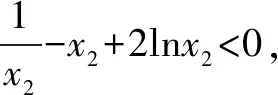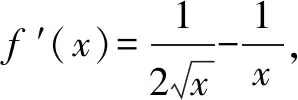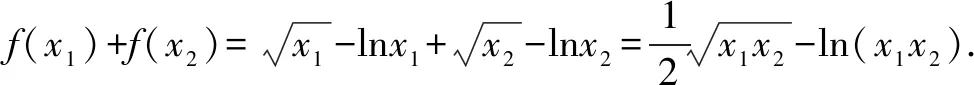賞析如出一轍的六道高考導函數題

武增明

(云南省玉溪第一中學 653100)

試題1 (2010年高考天津卷理科數學第21題)已知函數f(x)=xe-x(a∈R).

(1)求函數f(x)的單調區間和極值；

(2)已知函數y=g(x)的圖象與函數y=f(x)的圖象關于直線x=1對稱，證明：當x>1時，f(x)>g(x)；

(3)如果x1≠x2，且f(x1)=f(x2)，證明：x1+x2>2.

試題2 (2011年高考遼寧卷理科數學第21題)已知函數f(x)=lnx-ax2+(2-a)x.

(1)討論f(x)的單調性；

(2)設a>0，證明：

(3)若函數y=f(x)的圖象與x軸交于A，B兩點，線段AB中點的橫坐標為x0，證明：f′(x0)<0.

時隔僅一年，試題2竟然與試題1如出一轍.

(1)求函數f(x)的單調區間；

(2)證明：當f(x1)=f(x2)(x1≠x2)時，x1+x2<0.

時隔僅三年，試題3竟然與試題1如出一轍.

試題4 (2016年高考全國卷Ⅰ理科數學第21題)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點.

(1)求a的取值范圍；

(2)設x1，x2是f(x)的兩個零點，證明：x1+x2<2.

時隔僅三年，試題4竟然與試題3如出一轍.

(1)討論f(x)的單調性；

(1)若f(x)在x=x1，x2(x1≠x2)處導數相等，證明：f(x1)+f(x2)>8-8ln2；

(2)若a≤3-4ln2，證明：對于任意k>0，直線y=kx+a與曲線y=f(x)有唯一公共點.

時隔七年，試題5、試題6竟然與試題2如出一轍.

試題1賞析(1)f′(x)=(1-x)e-x.

令f′(x)=0，解得x=1.

當x變化時，f′(x)，f(x)的變化情況如下表：

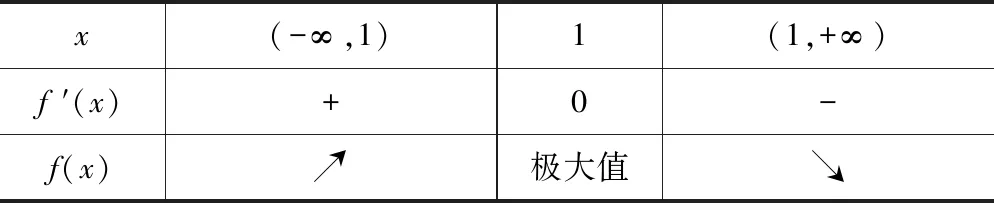
x(-∞,1)1(1,+∞)f ′(x)+0-f(x)↗極大值↘

所以f(x)在(-∞，1)內是增函數，在(1，+∞)內是減函數.

(2)證明由題意可知，g(x)=f(2-x)，得g(x)=(2-x)ex-2.

令F(x)=f(x)-g(x)，即F(x)=xe-x+(x-2)ex-2.

于是F′(x)=(x-1)(e2x-2-1)e-x.

當x>1時，2x-2>0，從而e2x-2-1>0，又e-x>0，所以F′(x)>0，從而函數F(x)在[1，+∞)上是增函數.

又F(1)=e-1-e-1=0，

所以x>1時，有F(x)>F(1)=0，即f(x)>g(x).

(3)證明①若(x1-1)(x2-1)=0，

由(1)及f(x1)=f(x2)，得x1=x2=1，與x1≠x2矛盾.

②若(x1-1)(x2-1)>0，由(1)及f(x1)=f(x2)，得x1=x2，與x1≠x2矛盾.

根據①，②，得(x1-1)(x2-1)<0，不妨設x1<1，x2>1，由(2)可知，f(x2)>g(x2)，g(x2)=f(2-x2)，所以f(x2)>f(2-x2)，從而f(x1)>f(2-x2).

因為x2>1，所以2-x2<1.

又由(1)可知函數f(x)在區間(-∞，1)內是增函數，所以x1>2-x2，即x1+x2>2.

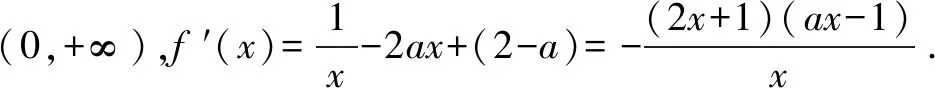
若a≤0，則f′(x)>0，所以f(x)在(0，+∞)單調增加.

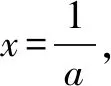
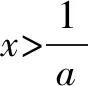
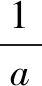
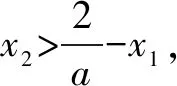
由(1)知，f′(x0)<0.

試題3賞析(1)函數f(x)的定義域為(-∞，+∞).

當x<0時，f′(x)>0；當x>0時，f′(x)<0.

所以f(x)的單調遞增區間為(-∞，0)，單調遞減區間為(0，+∞).

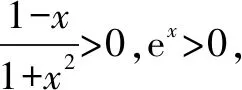
同理，當x>1時，f(x)<0.

當f(x1)=f(x2)(x1≠x2)時，不妨設x1

由(1)知，x1∈(-∞，0)，x2∈(0，1).

下面證明：

當x∈(0，1)時，g′(x)<0，g(x)單調遞減.

所以?x∈(0，1)，f(x)

而x2∈(0，1)，所以f(x2)

由于x1，-x2∈(-∞，0)，f(x)在(-∞，0)上單調遞增，所以x1<-x2，即x1+x2<0.

試題4賞析(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).

設a=0，則f(x)=(x-2)ex，f(x)只有一個零點.

設a>0，則當x∈(-∞，1)時，f′(x)<0；當x∈(1，+∞)時，f′(x)>0，所以f(x)在(-∞，1)上單調遞減，在(1，+∞)上單調遞增.

設a<0，由f′(x)=0得x=1或x=ln(-2a).

又當x≤1時，f(x)<0，所以f(x)不存在兩個零點.

因此f(x)在(1，ln(-2a))上單調遞減，在(ln(-2a)，+∞)上單調遞增.

又當x≤1時，f(x)<0，所以f(x)不存在兩個零點.

綜上，a的取值范圍為(0，+∞).

(2)不妨設x1

2-x2∈(-∞，1)，又f(x)在(-∞，1)上單調遞減，所以x1+x2<2等價于f(x1)>f(2-x2)，即f(2-x2)<0.

由于f(2-x2)=-x2e2-x2+a(x2-1)2，

而f(x2)=(x2-2)ex2+a(x2-1)2=0，

所以f(2-x2)=-x2e2-x2-(x2-2)ex2.

設g(x)=-xe2-x-(x-2)ex，則

g′(x)=(x-1)(e2-x-ex).

所以當x>1時，g′(x)<0，而g(1)=0，故當x>1時，g(x)<0.

從而g(x2)=f(2-x2)<0，故x1+x2<2.

若a≤2，則f′(x)≤0，當且僅當a=2，x=1時，f′(x)=0，所以f(x)在(0，+∞)單調遞減.

(2)由(1)知，f(x)存在兩個極值點當且僅當a>2.

由于f(x)的兩個極值點x1，x2滿足x2-ax+1=0，

所以x1x2=1，

不妨設x11.

x(0,16)16(16,+∞)g′(x)-0+g(x)↘2-4ln2↗

所以g(x)在[256，+∞)上單調遞增，故g(x1x2)>g(256)=8-8ln2，即f(x1)+f(x2)>8-8ln2.

(2)解略.

上述試題1、試題3、試題4的最后一問的證明方法都是使用函數的單調性定義來證明，試題2和試題5的第(2)問與試題6的第(1)問的證明方法都是尋找待證不等式的等價不等式，然后通過求導或構造函數求導，證明等價不等式.與上述試題1、試題2、試題3、試題4、試題5、試題6如出一轍的還有以下試題7，讀者不妨自己試一試.

試題7 (2018年全國高中數學聯賽福建賽區預賽題)已知f(x)=ex-mx.

(1)若x>0時，不等式(x-2)f(x)+mx2+2>0恒成立，求實數m的取值范圍；

(2)若x1，x2為函數f(x)的兩個零點，證明：x1+x2>2.