評價型無量綱法、自然權重與線性科技評價

俞立平 宋夏云

摘?要：[目的/意義]線性多屬性評價值一般情況下并不具備評價優劣的直接判斷功能，即不能根據評價得分判定優良或是否及格等，這個問題是個隱含問題，在科技評價中尤為突出，一直沒有得到足夠的重視。[方法/過程]本文在分析多屬性評價值評價功能的影響機制的基礎上，提出基于Sigmoid函數進行無量綱處理，在此基礎上分析其對自然權重與線性科技評價的影響，并基于JCR2017經濟學期刊進行實證。[結果/結論]研究結果表明：傳統情況下根據評價值直接判斷評價對象優劣是欠妥的;評價值的優劣判斷功能取決于評價指標無量綱法與評價方法;Sigmoid無量綱可以有效消除自然權重問題;無量綱方法不同會影響線性評價結果;對文獻計量指標采用極大值無量綱值得商榷;在科技評價中建議推廣Sigmoid函數無量綱法。

關鍵詞：無量綱法;Sigmoid函數;自然權重;線性評價;多屬性評價

DOI：10.3969/j.issn.1008-0821.2020.04.014

〔中圖分類號〕G302?〔文獻標識碼〕A?〔文章編號〕1008-0821（2020）04-0120-08

Evaluation Dimensionless Method，Natural Weight and

Linear Technology Evaluation

Yu Liping1?Song Xiayun2

（1.School of Statistics and Mathematics，Zhejiang Gongshang University，Hangzhou 310018，China;

2.School of Accounting，Zhejiang University of Finance and Economics，Hangzhou 310018，China）

Abstract：[Purpose/Significance]In general，the linear multi-attribute evaluation value does not have the direct judgment function of evaluating the superiority and inferiority，it cannot judge whether it is good or not based on the evaluation score.This problem is an implicit problem，which is particularly prominent in the evaluation of science and technology，and has not received enough attention.[Method/Process]Based on the analysis of the influence mechanism of multi-attribute evaluation value evaluation function，this paper proposed a dimensionless processing based on sigmoid function，analyzed its influence on natural weight and linear science and technology evaluation，and conducted an empirical study based on JCR2017 economics journal.[Result/Conclusion]The results showed that it was not proper to judge the quality of the evaluation object directly according to the evaluation value.The judgment function of evaluation value depended on the evaluation index dimensionless method and evaluation method.Sigmoid dimensionless could effectively eliminate the natural weight problem.Different dimensionless methods will affect the results of linear evaluation.The use of maximum dimensionless for bibliometrics questionable questionable.It was suggested to popularize the sigmoid function dimensionless in the science and technology evaluation.

Key words：dimensionless method;Sigmoid function;natural weight;linear evaluation;multi-attribute evaluation

在科技評價中，多屬性評價方法得到了廣泛的應用。多屬性評價通過建立指標體系，選取若干指標對評價對象進行綜合評價，避免了單一指標評價信息量不足的缺陷，從更廣泛的視角進行評價。加上多屬性評價方法眾多，各種評價方法特點不同，從而為達成評價目的提供了更多的選擇，所以現在多屬性評價已經廣泛應用在大學評價、科研機構評價、學術期刊評價、科研人員評價等領域。

評價指標優劣判斷標準是多屬性評價的基本問題。在多屬性評價中，有兩類評價指標，一類是評價型評價指標，其特點是存在理論上的極優值。比如科研效率，滿分為1，某機構效率為0.82，可以直接判斷該機構科研效率的優良。另一類是非評價型評價指標，其特點是并不存在理論上的極優值。比如某學科某學術期刊h指數極大值為75，人們無法根據這個值來直接判斷優良，因為h指數排名第一的期刊并不代表就是滿分，只能通過排名進行大致比較。目前絕大多數科技評價指標均是非評價型評價指標，所有這個問題的影響比較廣泛。

評價指標的優劣判斷標準問題會影響到多屬性評價值的優劣判斷。在多屬性評價中，評價指標往往首先要進行標準化或無量綱方法進行預先處理，其中用得最多的無量綱化方法是極大值法，即所有的評價指標均除以各自對應的極大值。對于非評價型指標而言，帶來的后果是多屬性評價值也屬于非評價型，即評價結果得分即使看上去是百分制得分，其實并不能按照這個分值來判斷優劣，只能進行排序。

自然權重問題是指由于指標無量綱后評價均值不等引起的實際權重差異問題。自然權重問題由俞立平[1]首先提出，以學術期刊評價為例，假設只采用總被引頻次和影響因子兩個指標進行評價，權重采用等權重，即期刊評價得分為總被引頻次與影響因子無量綱化后各乘以0.5進行加權匯總，但是總被引頻次與影響因子無量綱化后均值并不相等，假設總被引頻次無量綱化后均值為20，影響因子無量綱化后的均值為50，那么在實際評價中雖然是等權重，但總被引頻次由于均值較低明顯沒有得到重視，其實際權重只有影響因子的40%（20/50），這就是由于數據本身產生的問題，因此稱為自然權重，其根源是評價指標的數據分布及數據自身特點不同。

將評價指標的優劣判斷標準問題與自然權重問題放在一個框架下研究非常必要。評價指標的優劣判斷標準會影響多屬性評價值的判斷，自然權重會影響到多屬性評價中實際權重，進而影響評價結果，兩者均與評價指標的無量綱法密切相關。相關問題如果能夠得到改善，不僅可以豐富多屬性評價的基礎理論，推進無量綱方法與權重的研究，而且對于科技評價應用具有重要的實踐意義。

1?文獻綜述

評價型指標的優劣判斷標準本質上屬于無量綱方法問題。Lama N等[2]指出指標的無量綱化是開展綜合評價活動的基礎，包括線性無量綱化方法和非線性無量綱方法。王常凱等[3]針對縱橫向拉開檔次法中的無量綱問題，提出一種新的標準化方法，即無量綱化面向指標所有時間數據，標準化面向指標某一時間數據。蔣維楊等[4]針對大樣本評價，提出一種結合專家主觀經驗與客觀指標原始數據的無量綱化方法。郭亞軍等[5]提出逼近理想性質的復合無量綱化方法的原則，并構造了一種新的無量綱化方法——極標復合法。廖志高等[6]將非線性無量綱化方法分為3種類型，同時提出了反三角函數無量綱化方法，這也是一種非線性無量綱法。郭亞軍等[7]提出一種利用反正切函數或反余切函數構建的無量綱方法，認為其可較好保留原始數據包含的信息。慈鐵軍等[8]提出了一種基于決策者偏好的評價指標區間屬性值規范化方法。高瑞忠等[9]認為簡單非線性函數可以實現對于復雜函數的局部映射，提出采用復合Sigmoid函數方法來預測GDP。

關于無量綱法的選取，Chakraborty S等[10]通過對各種無量綱化法的對比研究，發現每種指標無量綱化法都有其特定使用場合，應根據不同情況進行選取。宮誠舉等[11]從群體信息最大程度擴大評價對象間差異的角度，提出群體信息集結過程中無量綱化方法選擇的若干建議。詹敏等[12]認為線性無量綱化方法應滿足差異比不變性、單調性、縮放無關性、穩定性和平移無關性，在此基礎上進行選取。李玲玉等[13]認為無量綱法選取必須遵循穩定性、差異性和變異性原則，認為線性比例法最適合于拉開檔次法。

關于指標無量綱法對多屬性評價的影響。Zhang L J等[14]分析了無量綱化方法對綜合評價結果影響的魯棒性。糜萬俊[15]基于離差最大化要求的假設沖突、約束條件以及可能造成權重信息失真的問題，從評價指標方差分析入手，分析了無量綱化方法對評價指標權重影響的傳導機制。王會等[16]分析了線性無量綱化方法對熵值法的影響，發現等差數列數據通過極值法無量綱化后權重不變，具有相同指標值的正向指標和反向指標權重不等，提出應根據原始指標數據運用熵值法確定權重。江文奇[17]分析了無量綱化方法對評價指標屬性權重的敏感性問題。蘇術鋒[18]認為數據差異大小不能反映指標的重要程度的高低，所以數據差異的客觀賦權法理論根據不足，是一種穩定性欠佳的存在瑕疵方法。

關于自然權重問題，俞立平[1]界定了自然權重的概念，分析其對設計權重、實際權重以及對線性評價結果的影響極值。俞立平等[19]分析自然權重對非線性評價方法的影響，提出動態最大均值逼近標準化方法，以消除自然權重的影響。

從現有的研究看，關于評價指標的無量綱方法的設計，學術界進行了大量的研究，涌現出許多新的線性或非線性無量綱方法，關于指標無量綱方法的選擇，學術界也總結出許多選取原則。至于評價指標無量綱法對多屬性評價影響，學術界已經認識到這個問題，研究涉及到評價權重、評價結果的靈敏度、評價結果的排序等等。自然權重問題是個新的問題，只有少數學者開展研究。總體上，關于評價指標的優劣判斷標準與自然權重問題，在以下幾個方面需要進一步進行深入研究：

第一，現有的無量綱方法對于評價值優劣標準判斷的影響機制，這個問題缺乏研究。

第二，從無量綱方法角度，需要進一步探索采用無量綱方法來解決評價指標優劣判斷標準問題。

第三，如果通過無量綱方法能適度解決評價指標優劣判斷標準，那么對于線性科技評價結果會產生哪些影響。

第四，如果通過無量綱方法在評價指標優劣判斷標準方面取得進展，那么其對自然權重會產生哪些影響，進而對評價結果產生哪些影響。

本文在分析無量綱方法對評價結果值影響機制的基礎上，提出基于Sigmoid函數的評價指標無量綱法，以解決評價指標的優劣判斷標準問題，并基于JCR2017經濟學期刊數據，采用CSSCI學術期刊的線性評價方法，分析Sigmoid無量綱法對評價指標、自然權重以及評價結果值的影響。

2?理論基礎與研究方法

2.1?評價指標優劣判斷標準失范對評價值的影響機制

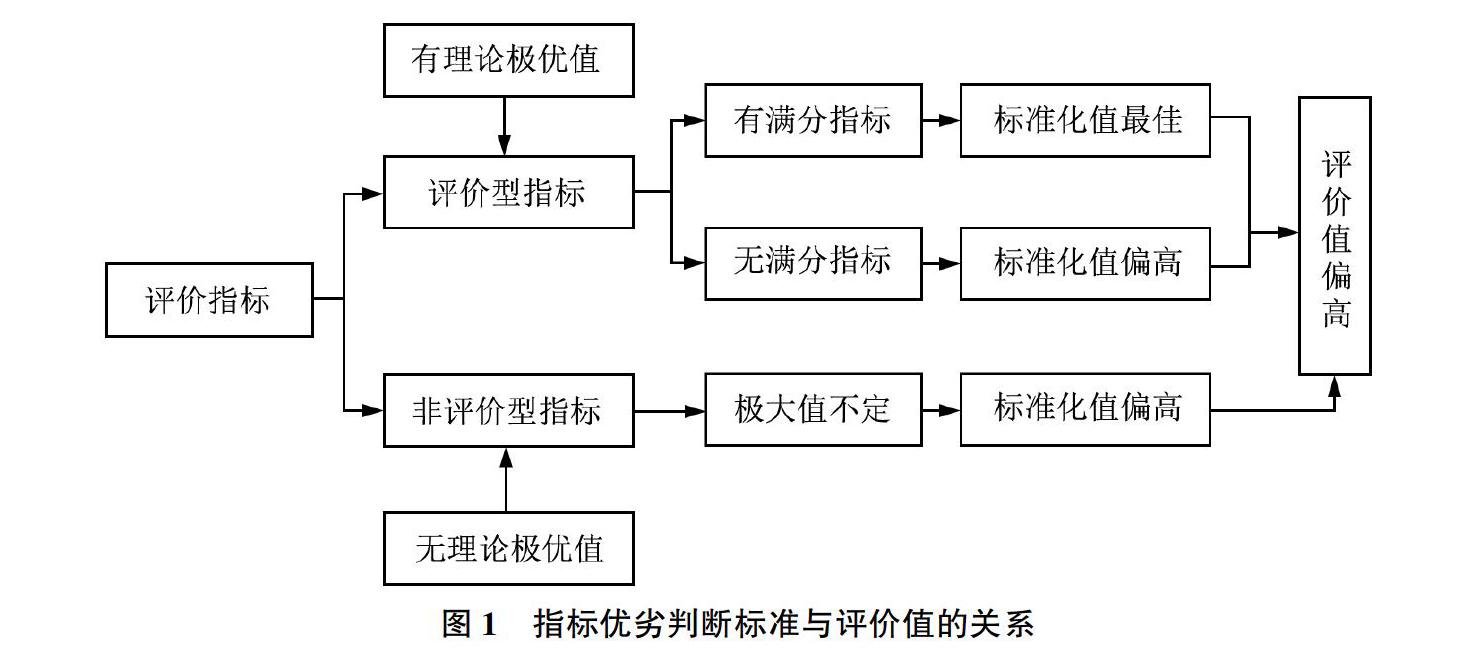
現有無量綱方法對評價結果值的影響機制如圖1所示。評價指標分為評價型評價指標與非評價型評價指標，評價型評價指標存在理論上的極優值，非評價型評價指標不存在理論上的極優值。

在多屬性評價中，對于所有指標均首先進行無量綱化處理，無量綱化方法采用最多的就是極大值法，即所有指標均除以其極大值。對評價型指標而言，如果其恰好有滿分，那么無量綱化后值為1，相當于也是滿分，既不高估也不低估。如果沒有滿分，比如滿分為100，但極大值只有90，那么無量綱化后其極大值也為1，需要注意的是，此時實際上將極大值高估了，本來是90，但現在是1。對于非評價型指標而言，由于其無理論極優值，基于理論極優值比現有極大值更高的假定，無量綱化后指標值其實是高估的。

綜合分析評價型指標與非評價型指標采用極大值無量綱化后的結果，指標無量綱化值更多情況下是高估的，只有在少數情況下才是適中的，即既不高估也不低估，這樣線性評價結果值肯定是高估的，這就是目前多屬性評價中普遍存在的問題。

既然多屬性評價結果值存在高估問題，那么根據評價結果得分進行深度分析就要慎重。比如在學術期刊評價中，某個雜志的最終得分為0.6，那么就不能簡單說該期刊已經達到及格線，實際情況肯定未達到，因為被高估了。

2.2?線性多屬性評價方法的優劣判斷問題

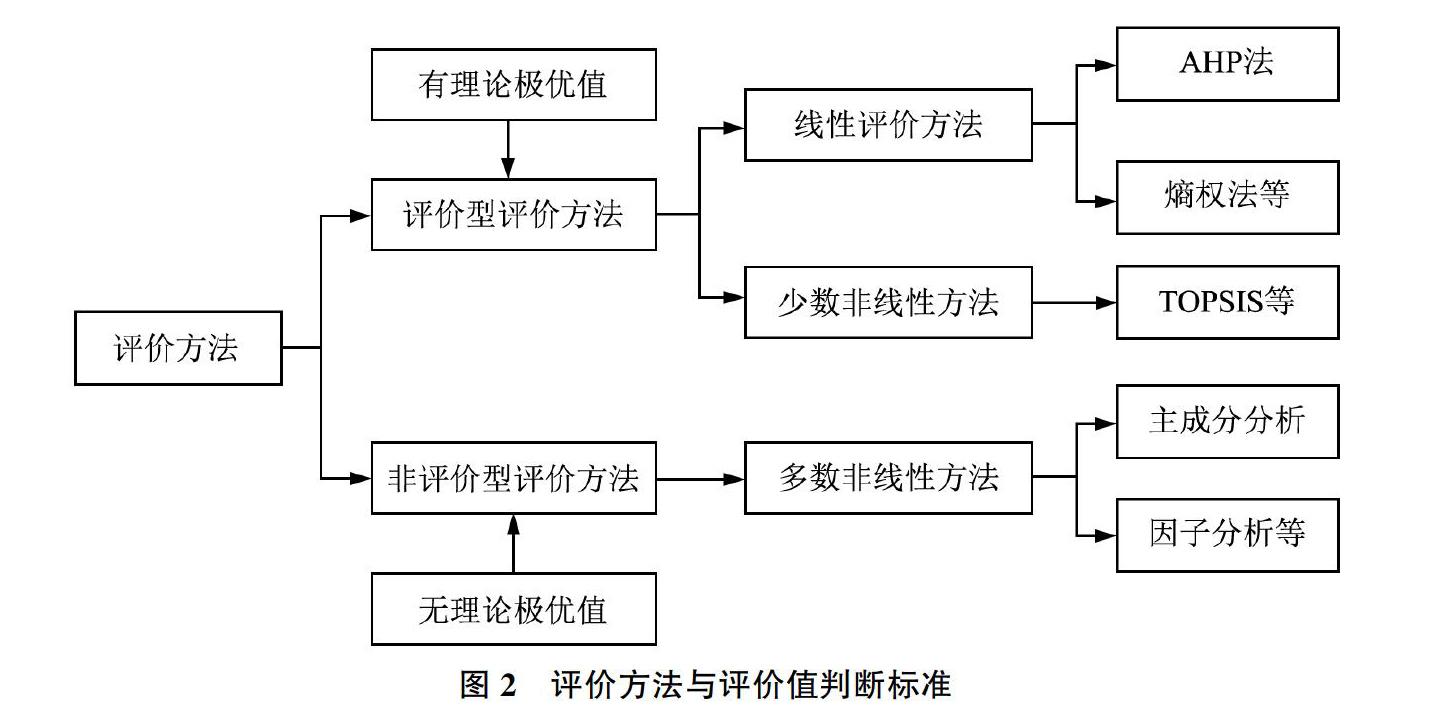
多屬性評價方法也有優劣判斷標準問題。對這個問題的界定學術界很少關注，本文將其稱為評價型評價方法：對于任意一種多屬性評價方法，在某個評價對象所有評價指標值均為極大值的情況下，如果其評價得分也為1（或100），那么該評價方法就是評價型評價方法，或者說，有理論上極優值的評價方法就是評價型評價方法。

評價型評價方法以線性評價方法和部分非線性評價方法為主。所有的線性評價方法均為評價型評價方法，如層次分析法AHP、熵權法、變異系數法、CRITIC法等等，另外少數非線性評價方法也屬于評價型評價方法，如TOPSIS，其評價理想極大值為1。非評價型評價方法主要以多數非線性評價方法為主，典型是主成分分析、因子分析等評價方法，這兩種方法的評價結果值均同時具有正值和負值，可以排序，但不能直接判斷優劣。

2.3?基于Sigmoid函數的無量綱方法

1920年，美國生物統計學家Pearl R等[20]研究美國自1790年以來人口增長問題，首次提出了Logstic曲線方程，也稱為成長曲線。成長曲線展示了事物產生、發展與壯大的過程，已經被廣泛應用在科技、經濟、社會、生物等諸多領域。成長曲線更多被應用在時間序列數據中，反映了事物隨時間的發展變化。換一種視角來說，對于某種事物的某類發展指標而言，其實可以采用截面數據來擬合成長曲線。這是因為任何事物都是從較小的時候發展過來的，現在較小的事物可以看作現在較大事物的過去，或者說，現在較大事物就是較小事物發展的未來。

成長曲線一般用Logistic函數表示，其通用表達式為：

Y=L1+ae-bt（1）

式（1）中，Y代表事物發展的水平，L表示事物發展的理論極大值，t表示時間，e表示自然對數，a、b為調節系數。

正因為Logistic曲線有理論極優值L，而這正是評價型無量綱法所必須的，所以基于成長曲線對評價指標無量綱具有指標優劣的直接判斷功能。

當L=a=b=1時，Logistic函數就變成Sigmoid函數，Sigmoid函數是成長曲線的一種特殊形式（見圖3）：

Y=11+e-1（2）

既然采用截面數據來模擬成長曲線，那么如何將截面數據轉化為時間就是一個關鍵問題。從圖3可以看出，當t在（-5，5）區間時，Y值在（0，1）之間變化，所以只要將截面數據通過某種轉換映射在（-5，5）之間即可，最有效的方法就是進行z值轉換：

z=X-μδ（3）

式（3）中，X為原始指標，μ為其平均值，σ為標準差。將z值代入Sigmoid函數，用其代替t就可以完成無量綱。

2.4?Sigmoid函數與自然權重

由于采用z值來代替Sigmoid函數中的時間t來進行無量綱化，因此對于正態分布而言，所有指標無量綱化后的均值均為0.5，即無量綱后所有指標的均值會相等，這樣就不存在自然權重問題，所以在評價指標服從正態分布時，采用Sigmoid函數進行無量綱化處理能夠解決自然權重問題。

在科技評價中，許多文獻計量指標并不服從正態分布[21-22]，在這種情況下，無量綱對自然權重的影響有待進一步分析，但總體上，Sigmoid函數作為一種非線性無量綱法，相比極大值無量綱法，應該還是能有所改善自然權重問題。

2.5?線性評價方法

為了對本文提出的思路與方法進行實證研究，本文以南京大學CSSCI學術期刊評價方法為例，選取總被引頻次與影響因子兩個指標，采用Sigmoid函數進行無量綱，然后采用線性評價方法進行評價，其計算公式為：

評價值=總被引頻次×0.2+影響因子×0.8（4）

很顯然式（4）是一種線性評價方法，當然顯然屬于評價型評價方法。

3?實證結果

3.1?數據來源

本文數據來源于JCR2017經濟學期刊，JCR2017公布的文獻計量指標有多個，本文選取總被引頻次與影響因子兩個指標進行評價。2017年入選JCR的經濟學期刊共有353種，由于有32種期刊存在數據缺失，將其刪除，實際還有321種期刊。

3.2?極大值無量綱與Sigmoid函數無量綱比較

極大值無量綱與Sigmoid函數無量綱結果如表1所示。從均值看，采用極大值無量綱總被引頻次和影響因子相差較大，分別為0.057和0.196，但采用Sigmoid函數無量綱均值趨于接近，分別為0.477、0.483。

從極大值看，采用極大值無量綱極大值肯定為1，但采用Sigmoid函數無量綱，總被引頻次的極大值為1，影響因子的極大值為0.994，說明影響因子尚未達到理論上的極優值。

從極小值看，采用極大值無量綱總被引頻次和影響因子的極小值均較低，分別為0.002、0.018，但采用Sigmoid函數無量綱極小值均較大，分別為0.382、0.244，也就是說，采用Sigmoid函數無量綱有效提高了極小值。

從離散系數看，采用極大值無量綱和Sigmoid函數無量綱，總被引頻次的離散系數分別為1.995、0.284，影響因子的離散系數分別為0.803、0.390，即采用Sigmoid函數無量綱降低了離散系數，數據分布更加均勻。

從數據分布看，采用Sigmoid函數無量綱降低了總被引頻次與影響因素的偏度S和峰度K，并且降低了Jarque-Bera檢驗值，雖然無量綱后也不服從正態分布，但采用Sigmoid函數無量綱使得總被引頻次和影響因子更加接近正態分布。

3.3?采用Sigmoid函數對自然權重的影響

只有在評價指標無量綱后均值相等的情況下才沒有自然權重問題，根據這個界定，采用極大值無量綱時，影響因子與總被引頻次之比為0.196/0.058=3.379，即影響因子的自然權重是總被引頻次的3.379倍，這個差距是巨大的。采用Sigmoid函數無量綱后，影響因子與總被引頻次之比為0.483/0.477=1.013，兩者接近相等，也就是說，采用Sigmoid函數無量綱已經基本上解決了自然權重問題。

由于總被引頻次和影響因子并不服從正態分布，但采用Sigmoid函數無量綱化后，兩者的均值仍然接近相等，說明即使在指標不服從正態分布的情況下，采用Sigmoid函數無量綱化仍然可以有效解決自然權重問題。

3.4?不同無量綱評價結果的比較

分別采用極大值無量綱與Sigmoid無量綱，然后分別進行評價，其描述統計結果如表2所示。結果與指標無量綱類似，即采用Sigmoid無量綱，提高了均值和極小值，降低了離散系數，使得評價結果值更加接近正態分布，這對評價是非常有益的。

由于采用Sigmoid函數無量綱具有評價值的優劣直接判斷功能，從結果看，有73種期刊位于及格水平以上，及格率為22.67%;而采用極大值無量綱，位于及格線以上的期刊僅有9種，及格率為2.80%。由于極大值無量綱在理論上高估了評價值，因此這種及格率仍然是高估后的結果。當然這種情況產生的原因是文獻計量指標的數據分布問題，所以在這種情況下采用極大值無量綱有待進一步商榷。

不同無量綱方法評價結果如表3所示，由于篇幅所限，本文僅公布了按Sigmoid函數無量綱進行評價后，排序前30位的期刊。由于采用Sigmoid無量綱方法，也改變了極大值無量綱的評價結果排序。

4?研究結論

4.1?傳統情況下根據評價值直接判斷評價對象優劣是欠妥的

只有在理論上具有極大值的評價指標才是評價型評價指標，但是在科技評價中，由于大多數評價指標并不是評價型指標，即不能根據無量剛化后的值直接判斷優劣，加上許多評價方法也并非評價型評價方法，所以此時多屬性評價值是沒有直接評價功能的，即不能根據評價值的大小來判斷其優良，以及是否及格等等，只能進行排序。但在實際評價工作中，由于這個問題是隱含的，評價值被過分解讀，很明顯這是值得商榷的。

4.2?評價值的優劣判斷功能取決于評價指標無量綱法與評價方法本文分析了評價值優劣判斷功能的影響機制，認為其受評價指標無量綱化方法與評價方法的影響。對于評價指標無量綱方法，可以分為評價型無量綱法與非評價型無量綱法，采用前者無量綱才具有評價指標及后續的評價值的優劣判斷功能。對于多屬性評價方法，也可以分為評價型評價方法與非評價型評價方法，所有的線性評價方法與少數非線性評價方法屬于評價型評價方法，而多數非線性評價方法如主成分分析、因子分析屬于非評價型評價方法。只有同時采用評價型無量綱法與評價型評價方法的評價值，才具有直接根據評價值進行優劣判斷的功能。

4.3?Sigmoid無量綱可以有效消除自然權重問題

本文研究發現，采用Sigmoid函數無量綱，不同指標的均值有接近趨勢，即使在評價指標不服從正態分布的情況下，這樣可以有效消除由于某個指標均值過低導致其在多屬性評價值中比重過小問題，即自然權重問題。由于自然權重是隱含的，會導致評價實際權重偏離專家設定權重或采用某種主客觀方法確定的權重，產生隱含的不公平現象，Sigmoid函數無量綱為解決這個問題提供了一種較好的思路。

4.4?無量綱方法不同會影響線性評價結果

無量綱方法不同也會影響線性評價結果，尤其在評價對象較多，評價對象之間區分度相對較低的情況下。本文的實證研究結果表明，即使對于那些評價分值較高的評價對象，無量綱方法不同也會使得評價排序發生較大的變化。

4.5?對文獻計量指標采用極大值無量綱值得商榷

盡管學術界公認文獻計量指標的數據分布是有偏的，但是從評價的角度，如果評價值的偏態很嚴重，就要認真考慮無量綱方法以及評價方法。本文研究發現，采用極大值無量綱評價時，期刊及格率在高估的情況下只有2.80%，遠遠低于采用Sigmoid函數無量綱后評價值的22.67%的水平。如果基于前者的評價結果，難道經濟學期刊的質量差距真有那么大嗎？此時應該對極大值無量綱進行反思，因為與客觀事實嚴重不符。

4.6?在科技評價中建議推廣Sigmoid函數無量綱

基于Sigmoid函數無量綱，不僅解決了評價值的優劣直接判斷問題，使得多屬性評價值有可能具備優劣判斷功能，而且提高了評價均值，降低了離散系數，使得數據分布更加均勻，同時評價值更加接近正態分布，這對學術評價而言是非常重要的，建議對于非評價型評價指標，可以采用Sigmoid函數進行無量綱，進而進一步進行多屬性評價。

由于本文基于JCR經濟學期刊和CSSCI評價方法分析評價型無量綱法、自然權重的相關問題，從而得出以上結論，至于其他學科的學術期刊是否會得出類似的結論，有待進一步研究。

參考文獻

[1]俞立平.線性科技評價中自然權重問題及修正研究——動態最大均值逼近標準化方法[J].統計與信息論壇，2018，33（10）：27-33.

[2]Lama N，Boracchi P，Biganzoli E.Exploration of Distributional Models for a Novel Intensity-Dependent Normalization Procedure in Censored Gene Expression Data[J].Computational Statistics and Data Analysis，2009，53（5）：1906-1922.

[3]王常凱，鞏在武.“縱橫向”拉開檔次法中指標規范化方法的修正[J].統計與決策，2016，（2）：77-79.

[4]蔣維楊，趙嵩正，劉丹，等.大樣本評價的定量指標無量綱化方法[J].統計與決策，2012，（17）：4-9.

[5]郭亞軍，易平濤.線性無量綱化方法的性質分析[J].統計研究，2008，（2）：93-100

[6]廖志高，詹敏，徐玖平.非線性無量綱化插值分類的一種新方法[J].統計與決策，2015，（19）：72-76

[7]郭亞軍，宮誠舉，李偉偉，等.基于反三角函數的非線性預處理方法[J].系統工程，2017，35（7）：53-57.

[8]慈鐵軍，劉曉瑜.基于決策者偏好的區間數多屬性決策屬性值規范化方法[J].統計與決策，2015，（3）：36-38.

[9]高瑞忠，李和平，格日樂，等.基于復合Sigmoid函數的國內生產總值預測方法[J].工業技術經濟，2010，29（10）：101-104.

[10]Chakraborty S，Yeh C H.[IEEE Industrial Engineering（CIE39）-Troyes，France （2009.07.06-2009.07.09）]2009 International Conference on Computers & Industrial Engineering-A simulation comparison of normalization procedures for TOPSIS[C].2009：1815-1820.

[11]宮誠舉，郭亞軍，李玲玉，等.群體信息集結過程中無量綱化方法的選擇[J].運籌與管理，2017，26（5）：151-157.

[12]詹敏，廖志高，徐玖平.線性無量綱化方法比較研究[J].統計與信息論壇，2016，31（12）：17-22.

[13]李玲玉，郭亞軍，易平濤.無量綱化方法的選取原則[J].系統管理學報，2016，25（6）：1040-1045.

[14]Zhang L J，Tao L.A Research on Methods of Robust Measurement of Multi-index Comprehensive Evaluation Model[J].Statistics & Information Forum，2011，26（5）：16-20.

[15]糜萬俊.無量綱化對屬性權重影響的傳導機制及調權研究[J].統計與決策，2013，（4）：11-14.

[16]王會，郭超藝.線性無量綱化方法對熵值法指標權重的影響研究[J].中國人口·資源與環境，2017，27（S2）：95-98.

[17]江文奇.無量剛化方法對屬性權重影響的敏感性和方案保序性[J].系統工程與電子技術，2012，34（12）：2520-2523.

[18]蘇術鋒.客觀評價法中的數據差異賦權有效性及實證[J].統計與決策，2015，（21）：74-76.

[19]俞立平，宋夏云，王作功.自然權重對非線性科技評價的影響及糾正研究——以TOPSIS方法評價為例[J].數據分析與知識發現，2018，2（6）：48-57.

[20]Pearl R，Reed L J.On the Rate of Growth of the Population of the United States Since 1790 and Its Mathematical Representation[J].Proceedings of the National Academy of Sciences，1920，6（6）：275-288.

[21]Vinkler P.Introducing the Current Contribution Index for Characterizing the Recent，Relevant Impact of Journals，Scientometrics，2008，79（2）：409-420.

[22]Seglen P O.The Skewness of Science[J].Journal of the American Society for Information Science，1992，43（9）：628-638.

（責任編輯：郭沫含）