淺淺深深：數學教學之道

李潔 李柱俊

[摘要]“教什么”和“怎么教”一直是課堂教學的核心，對這兩個方面的把握應該遵循“深淺之道”：教學內容的深淺選擇應遵循教學目標和知識內容的本質;教學路徑應遵循學生認知基礎和認知規律的由淺入深。以“加法交換律和結合律”的教學為例，闡述如何在“深”“淺”之間進行轉化，尋找適合學生的教學，呈現由“淺”而及于“深”，又因“深”而歸于“淺”的教學。

[關鍵詞]教什么;怎么教;深淺之道

[中圖分類號]G623.5 [文獻標識碼]A [文章編號]1007-9068（2020）08-0017-02

數學課堂教學的核心離不開“教什么”和“怎么教”，而這兩方面都應該遵循“深淺之道”。因為無論選擇什么教學內容，其深淺都應遵循課程標準、基于教學目標和知識的發展軌跡與本質;無論選擇什么樣的教學路徑，亦應遵循學生由淺入深的認知基礎和認知規律。深深淺淺教數學，是數學的教學之道。下面以蘇教版教材四年級下冊“加法交換律和結合律”為例，進行“深”和“淺”之間轉化的教學。

一、教什么——理法淺入。本質深“扎”

教材中，給出“跳繩有多少人”這一問題，然后在得到等式28+17=17+28后，通過舉例歸納得出加法交換律是成立的。加法結合律的教學用的是同一幅主題圖，探索、發現的流程與加法交換律如出一轍。

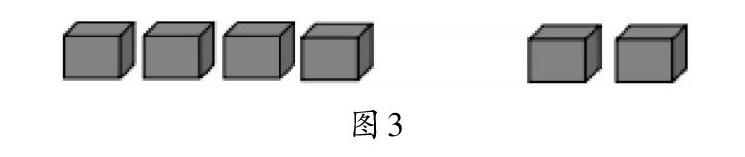
其實學生對加法交換律和結合律是有一定認知基礎的。如對于一年級“澆花的一共有多少個小朋友”（如圖1），因為還沒有正式學過用一個加法算式來表示，故大部分學生是用“數數”累加的方法，并且發現先數左邊3人再接著數右邊2人，與先數右邊2人再接著數左邊3人，其結果是一樣的，這樣的學習經歷就是加法交換律的“雛形”。之后，學生又在多位數加法驗算中多次經歷加數位置的交換（如圖2）。隨著學習經驗的不斷積累，學生會漸漸將“規律”內化成自己的認知經驗。

對于加數的結合，學生在學習一位數加一位數及整十數加兩位數的口算中也早已有了接觸。如9+7=9+（1+6）=（9+1）+6=10+6=16;48+37=48+（30+7）=（48+30）+7=78+7=85。基于以上對學生已有知識基礎的分析，如果教學該內容時還是按照教材編寫的流程——通過不完全歸納的方法總結出加法這兩個運算律，那對學生而言就沒有趣味性和挑戰性可言了，自然不利于學生學習力的提升，這樣的課堂教學顯然是低效的。那么，課堂教學應該如何定位？這節課應該教什么？課程標準指出，要關注“過程與方法的教學目標”，但凡是學生能夠明白的道理，課堂教學就要讓他們學會說理。因此，這節課應正本清源，需結合運算的意義，使學生深刻理解運算律的本質。

二、怎么教——意義淺入。數形深“刻”

加法運算中如何才能讓學生明白“為什么可以交換兩個加數”的道理呢？筆者以為，還得從加法的意義入手。自然數的加法，其本源意義在于對兩個具有有限基數且不相交的集合A和B作并集AUB之后，AUB的基數是A的基數與B的基數之和。誠然，這種抽象的說法是沒法讓四年級學生明白的，但是可以通過“數數”的形式，讓學生直觀感受到交換律的成立道理。

1.結合加法意義說理

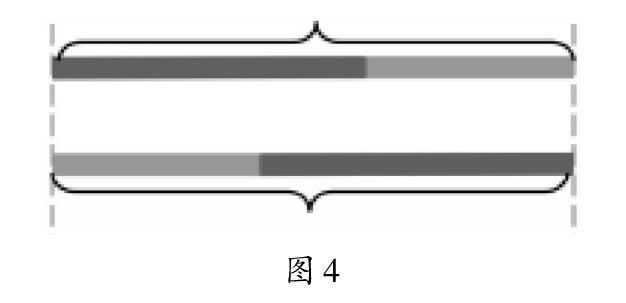
引入：你們想過在加法中為什么會存在把兩個加數的位置進行交換，和不變嗎？今天的學習就要弄清這其中的道理。（出示圖3）

提問：左邊有4個方塊，右邊有2個方塊。能數一數這里一共有幾個方塊嗎？

交流：他是按怎樣的順序數的？可以用算式表示出他數的過程嗎？（板書：4+2 2+4）

說明：兩次數的順序不同，但都是把兩部分合起來了，小方塊的總數沒有變，所以這兩道算式的和一定是不變的。（板書：4+2=2+4）

（數方塊活動說清楚了“交換兩個加數的位置，和不變”是合理的）

提問：可以再舉一個這樣的例子來解釋嗎？

交流：這樣的例子能舉得完嗎？老師這里有一幅圖可以把所有的例子都包含在內。（出示圖4）

提問：能試著說說這幅圖想表達的意思嗎？

交流：這里的兩條線段可以分別看成兩個加數，它們可以是怎樣的數呢？

2.描述加法交換律

引導：我們通過說理解釋了“交換兩個加數的位置，和不變”的道理，這其實是加法運算中的一條規律，你能給它起個名字嗎？

提問：加法交換律的等式可以寫出無數個，但也可以只用一個等式就能把所有這樣的等式都表示出來，你能創造出這樣的等式嗎？

說明：一般情況下，人們習慣用字母a和b來表示加法交換律，即a+b=b+a（這樣的一道字母式子就表示出了所有的例子，數學語言真是簡約啊！）

提問：在這一規律中，變化的是什么？不變的是什么？

交流：你們現在知道以前在驗算加法計算時為什么可以交換兩個加數的位置了吧？其實就是應用了加法交換律。

“數數”的過程淺顯易操作，直條圖直觀明了，教學時就是通過這樣淺顯直觀的形式使學生深入認識加法交換律的本質。這樣的數形結合思想對于學生理解加法運算律具有淺入深出的價值。

3.拓展加法交換律

交流：兩個加數交換位置，和不變。由此，你們還能想到什么？

引導（發給每個學生三種規格的方格紙各1張。如圖5）：你能用這三張方格紙拼成一個大長方形嗎？

學生可能出現的拼法：

提問：a+b+c是什么圖形？是怎么拼成的？b+c+a、c+a+b呢？

啟發：也可以把每種拼法反過來，就又會出現三種拼法。

提問：這6道算式都相等嗎？為什么？

引導：可以把任意兩道算式用等號連接起來，如

a+b+c=b+c+a。

啟發：看來，三個數相加也有交換律，那四個數、五個數呢？

說明：只要是連加，無論幾個加數，交換它們的位置，和不變。看來，加法交換律的內容可以改成——幾個數相加，交換加數的位置，和不變。

4.認識加法結合律

交流：在a+b+c=b+c+a這個等式中，前一個算式a+b+c中，我們先算的是哪兩個數的和？后一個算式b+c+a中，我們又先算哪兩個數的和？

引導：計算時就要先算括號里的，這是我們已經掌握的數學知識。a+（b+c）其實跟b+c+a相同，這種不改變加數的位置，通過添加括號改變計算順序保持結果不變的規律就是加法的結合律，用字母公式表示就是a+b+c=a+（b+c）。

提問：仔細觀察，在a+b+c=a+（b+c）中，什么變了？什么沒變？

5.驗證加法結合律

交流：假如這里的a表示16，b表示12，c表示4，我們把結合律這個等式中的a、b、c換成具體的數來算一算，看看是否真的相等。

說明：從剛才的學習中我們發現，幾個數連加的交換律、結合律其實是用不同的方法來改變計算的順序，本質上是相同的，只是方法不同。

a+b+c=b+c+a：交換加數位置，改變計算順序

a+b+c=a+（b+c）：添加括號，改變計算順序

不管怎樣拼，拼出的長方形的大小都是一樣的，這樣“淺”的操作使學生深刻明白了加法交換律在三個及以上數相加時是同樣適用的。同時，讓學生根據給定的算式說出具體拼的過程，使學生能直觀理解結合的意義，即先做什么，后做什么，讓學生深入明白“一起計算三個數，是有一定順序的，不像兩個數相加，只存在位置上的變化，不存在順序上的改變”。在這樣的教學中，學生容易感知結合律就是交換律的拓展和延伸，從而真正體會到結合律產生的必要性和價值，更加突出了加法交換律和結合律之間的聯系和區別。

遵循深淺之道的教學是基于課程標準、貼近學生、高于教材、淺入深出的教學，是由“淺”而及于“深”，又因“深”而歸于“淺”的精彩呈現。這樣的課堂回歸了數學教學的本真，回到了“對數學本質深刻理解”的最根本的數學使命上來。