一道競賽試題的解法探究及其應用

廣東省中山市濠頭中學 (528437) 閆 偉

1.試題呈現

例1 (2019年全國高中數學聯賽四川預賽試題)設點A的坐標為(0,3)，點B,C為圓O:x2+y2=25上的兩動點，滿足∠BAC=90°，求ΔABC面積的最大值．

分析：本賽題以圓為背景，考查了圓的標準方程、幾何性質、不等式等知識以及轉化、數形結合等數學思想，突出考查學生對數量關系進行轉化與運算能力以及推理論證能力，對考生的思維水平和數學素養有較高的要求；試題平中見奇，內涵豐富，解法多樣，是一道值得探究的好題.

2.解法探究

解法1：如圖1所示，設B(x1,y1),C(x2,y2),P(x,y)為線段BC的中點，則有

圖1

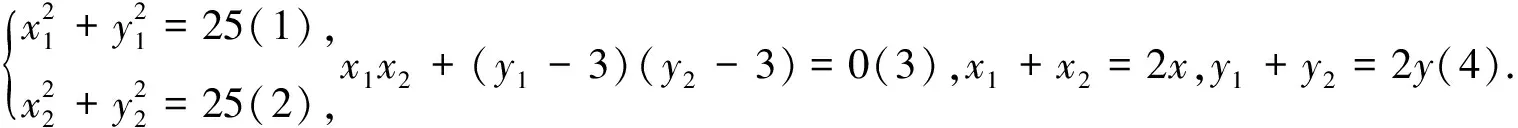
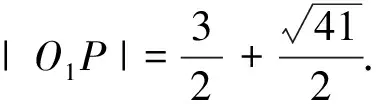
評注：本解法是參考答案提供的，在解決過程中先利用B,C點坐標確定線段BC中點P的軌跡，再根據點P的軌跡計算中線長AP的范圍，然后利用均值不等式將直角三角形的面積轉化成關于三角形斜邊中線的表達式，體現了轉化的思想及坐標法的運用.

圖2

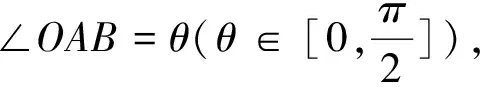
評注：解法2從三角函數的視角解題，引入角∠OAB作為參變量，根據定長OA計算點O到兩直角邊的距離，然后根據勾股定理用角∠OAB表示兩直角邊AB,AC從而得出面積關于參變量的表達式，再利用柯西不等式和三角恒等變換解決面積最大值；相比較解法1，雖然運算量不少，但利用函數和不等式的思想方法是解決幾何中最值的常用方法，這種通性通法在數學解題中起著至關重要的作用，在平時的解題教學中要注重這種通性通法，重視知識的生成過程，培養學生分析、解決問題的能力.

圖3

先給出矩形的一個性質：如圖3，已知P為矩形ABCD內一點，則|PA|2+|PC|2=|PB|2+|PD|2.

證明：以AB,AD所在直線為x,y軸建立平面直角坐標系，設A(0,0),B(a,0),C(a,b),D(0,b)，另設P(x,y)，則有|PA|2+|PC|2=x2+y2+(x-a)2+(y-b)2,|PB|2+|PD|2=(x-a)2+y2+x2+(y-b)2,顯然有|PA|2+|PC|2=|PB|2+|PD|2.下面用此結論解決上面的賽題.

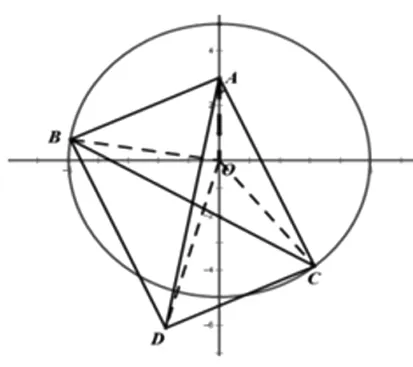
圖4

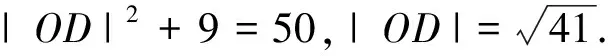
評注：解法3借助了平面幾何中矩形的一個優美結論，先通過直角構造矩形，利用矩形結論確定OD長度和矩形對角線AD，再引入∠CAD作為參變量表示三角形的面積，結合三角形的邊與邊關系建立面積的不等式，從而計算面積最大值；本解法相比較前2種解法，純粹從平面幾何的角度思考，巧借矩形結論，簡化了推理和運算過程，具有直觀、簡潔的特點，方法新穎獨到.在各類試題中具有隱性矩形的問題可以參考此法.

3.拓展應用

上述解法是借助矩形的性質巧妙解決了與面積相關的線段長度問題，進而達到解決面積最值這一目標；解析幾何通常用代數的工具解決幾何問題，平常解題中我們注重解幾的代數運算，輕視了幾何推理；實質上解析幾何問題的本質是幾何問題，它們本身包含一些重要的幾何性質，若能挖掘出題目中蘊含的平面幾何元素，充分利用平面幾何知識，則可以避開繁瑣的運算，使解題過程簡化，方法簡潔優美，更好的揭示這類問題的幾何性質.因此，解析幾何問題應該將解析法與平面幾何方法相結合，通過深思引領運算，從而得到解題的最優方法，這不僅是解決幾何問題減少運算的法寶，還可以更好的提高解題能力 .下面就這一性質的應用做些拓展研究，能快速有效的解決這一類問題，可謂是“小結論，大用途”.

圖5

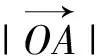
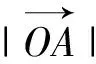
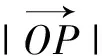
圖6

例3 如圖6，在平面坐標系xOy中，已知B,C為圓x2+y2=4上兩點，點A(1,1)，且AB⊥AC,則線段BC的長度的取值范圍是.

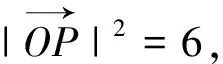
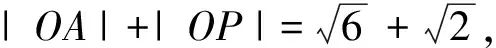
評注：通過直角關系構造矩形,結合矩形性質確定動點P的軌跡方程，再將線段BC的長度轉化成動點P與兩定點O、A的距離的關系從而得出結果，解題過程直觀、簡潔.

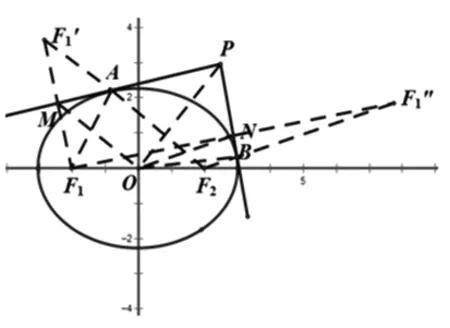
圖7

解：如圖7,設橢圓的左右焦點為F1,F2,設PA,PB與橢圓相切(切點為A,B)，且PA⊥PB.作F1關于PA,PB的對稱點分別為F1′,F1″，連接F1F1′,F1F1″分別于PA,PB交于M,N兩點.由橢圓的光學性質可知：F1,A,F2三點共線，F1″,B,F2三點共線.因為|F2F1′|=|AF1|+|AF2|=2a,所以得|OM|=a；同理|F2F1″|=

|BF1|+|BF2|=2a,得|ON|=a，由于F1MPN為矩形，于是有|OF1|2+|OP|2=|OM|2+|ON|2,所以|OP|2+c2=2a2，又c2=a2-b2，故|OP|2=a2+b2,從而點P的軌跡方程為x2+y2=a2+b2.

評注：上述結論中的點P的軌跡就是著名的蒙日圓,借助矩形的性質和橢圓的光學性質可以快速的得到結論，相比較傳統的方法利用切線的斜率作為參量，聯立直線與橢圓計算而言，極大的減少運算和推理論證過程，充分體現了妙用平面幾何性質巧解解析幾何問題的思想方法.

5.結語

數學家波利亞曾說過：“掌握數學就意味著善于解題” .引導學生學會解題是數學新課標教學的重要組成部分；數學問題的解決僅僅是一個開端，更重要的是解題后的反思與回顧；遇到一道經典題目，需要從多角度、深層次探求其解法，從不同的思維角度分析同一道試題，可以得到不同的解法，從數學知識本身的角度看，可以發現知識之間的相互聯系，體會轉化的過程，還可以構建知識網絡體系，從而學生在學習過程中不僅掌握了基本的解題技能，還培養了思維的廣闊性、深刻性、靈活性以及創新性，讓學生對學習內容有一個整體認識，并將知識融會貫通，舉一反三，開闊視野，活躍思維，才能實現解題研究價值的最大化.