快速收斂參考獨立分量分析方法
賈雁飛,杜艷麗,趙立權
1.北華大學 電氣與信息工程學院,吉林 吉林132013
2.東北電力大學 電氣工程學院,吉林 吉林132012
1 引言
獨立分量分析方法是一種解決混合信號分離的新穎方法,它僅僅只利用原始信源信號之間的非高斯,而且相互統計獨立的特性,從觀測到的原始信號的混合信號中分離出所有的原始信號,相對現有的信號分離方法結構更簡單,效果更好。參考獨立分量分析是為了解決獨立分量分析中不能單獨分離出某個或者多個感興趣的信源信號而提出來的。相對獨立分量分析,參考獨立分量分析在某些應用環境中,更適合實際應用。例如語音信號提取中,可能對其中部分語音信號感興趣,如果采用獨立分量分析方法,則必須提取出所有的語音信號,然后后期再從提取的語音信號中找出感興趣的語音信號,整個過程比較繁瑣,計算量較大。采用參考獨立分量分析,僅需要將擬提取的感興趣的語音信號的特征融入到參考獨立分析中,則可以直接提取出感興趣的語音信號,尤其是當原始信號數量較多的時候,采用參考獨立分量分析方法提取信號相對基于獨立分量分析方法具有明顯的優勢。
目前參考獨立分量分析方法已經被應用于圖像處理、語音信號提取、通信信號提取等多個領域[1-5]。現有的參考獨立分量分析主要從降低誤差、提高抗噪聲能力、提高信號分離的成功率以及收斂速度等角度進行了研究[5-11]。雖然可以利用收斂階數更高的牛頓迭代方法的對其代價函數進行優化[12-13],有效降低了算法的迭代次數,但是算法的復雜度也增加很大,因此收斂速度提高的程度受限。
為此,本文對現有牛頓迭代方法進行了研究和分析,提出采用結構簡單,且具有階收斂速度的牛頓迭代方法[14]對預處理后的參考獨立分量分析代價函數進行優化,推導出收斂速度更快的參考獨立分量分析方法。
2 參考獨立分量分析
參考獨立分量分析從獨立分量分析演進得到的,其代價函數類似獨立分量分析的代價函數,其代表函數表達式如下[15]:

式中,G 是一個非線性函數,其表達式與獨立分量分析中給出的非線性函數表達式一樣,y 是估計出的信源信號,v 是與估計出的信源信號y 具有相同均值和方差的高斯隨機信號,ρ 僅僅是一個值為正的常數,J(y)即為獨立分量分析的代價函數;g(y)是參考獨立分量分析算法融入到獨立分量分析算法中的一個約束函數,用來度量估計出的信源信號與參考信號之間的相似度,h(y)是用來約束估計出的信號方差,使得估計出的信源信號方差為1,避免每次估計出的信源信號具有不相同的方差。
參考獨立分量分析算法在代價函數中引入松弛因子,將式(1)中的不等式約束條件轉變成等式約束條件,其表達式如下:
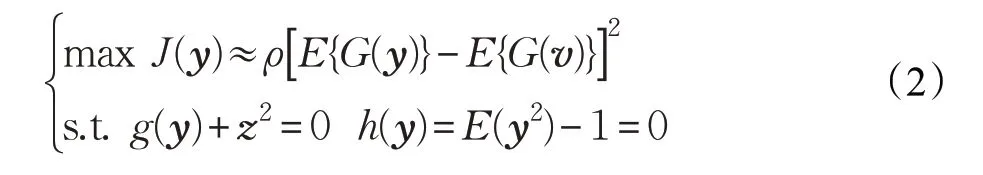
采用拉格朗日乘法方法將上式約束條件轉化成如下表達式:
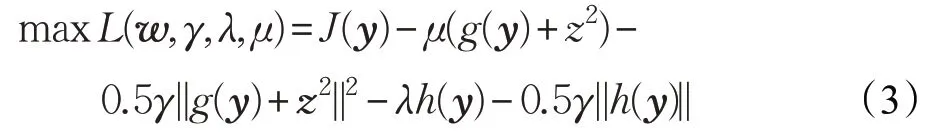
式中,y=wTx 是分離信號,w 是分離向量,x 是是觀測觀測信號,γ 是懲罰因子,μ 和λ 為拉格朗日乘子。對其上各變量進行優化,可以將(3)式轉換成如下表達式:
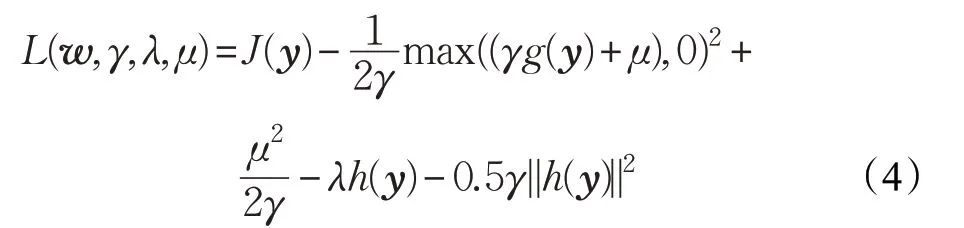
參考獨立分量分析采用傳統的牛頓迭代方法對(4)式進行求解,求解過程中的分離矩陣迭代表達式如下式所示:

式中,η 是固定的步長參數,Rxx是觀測信號的自相關矩陣,k 是迭代過程的當前迭代次數,和分別是L(w,γ,λ,μ)對當前迭代分離向量wk的一階和二階導數。其具體表達式如下:
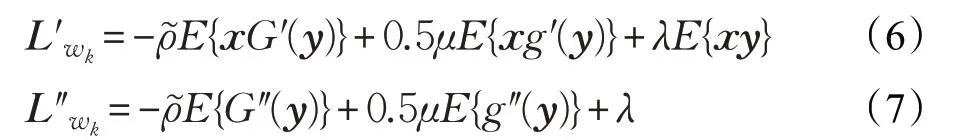
式中,G′(y)是非線性函數G(y)的一階導數,G″(y)是非線性函數G(y)的二階導數。g′(y)是非線性函數g(y)的一階導數,g′(y)是非線性函數g(y)的二階導數。參數μ 和λ 的迭代更新公式表示如下:
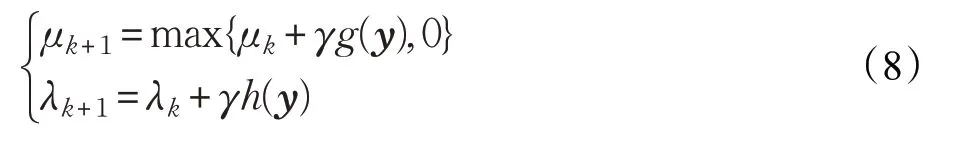
3 改進的參考獨立分量分析
根據式(5)可知,參考獨立分量分析在分離向量迭代過程中需要計算觀測信號的相關矩陣的逆矩陣,并且每次迭代需要計算該逆矩陣與其他矩陣的乘積,增加了算法的計算量。為此,本文借鑒文獻[7]的思想,采用白化的方法對觀測到的混合信號進行預先處理,假設觀測信號為z,則經過白化處理后的信號可以表示為:

式中,B=Σ-1/2U,Σ 為觀測信號的協方差矩陣的逆矩陣進行特征值分解得到的特征值矩陣,U 為特征向量矩陣。通過白化預處理方法使得處理后的信號均值為零,方差矩陣為單位矩陣,因此只要限制白化后信號的分離向量為正交矩陣,即可實現原算法約束分離信號的信號方差為1的限制。因此經過白化處理后,參考獨立分量分析的代價函數數學表達式可以表示成如下的形式:式中,各參數的表達含義與式(2)相同。同樣采樣拉格朗日方法對上式進行處理可得:
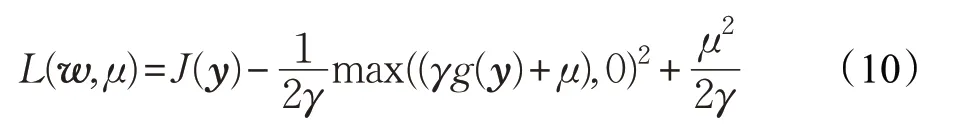
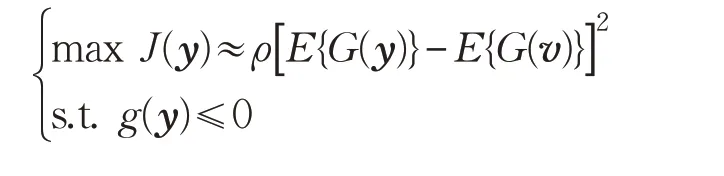

式中,w0是初始化的分離向量,w1是在初始化值的基礎上得到的對分量向量的初始估計向量:
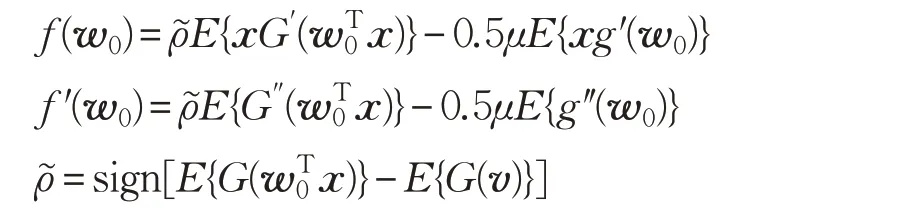
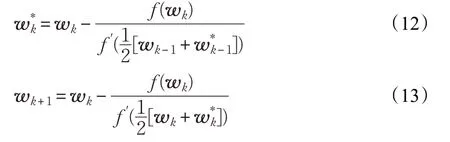
式中,f()和f′()分別是式(10)對分離向量w 的一階和二階導數。
本文提出改進方法中式(11)與文獻[7]的分離向量迭代更新公式相同,但是本文僅僅將其作為初始化分離向量的重新初始化,分離向量迭代更新公式采用式(12)和(13)進行。公式(11)也就是文獻[7]算法需要分別計算法一次代價函數一階導數和二階導數,假設導數的計算量相同,在忽略其他除法和加法的計算量的基礎上(導數的計算量遠大于其他計算量),文獻[7]一次迭代的計算量為2n。本文提出的方法初始化時的計算量為2n,第一次迭代的計算量為3n,第二次迭代過程中由于已經存儲前一次,則其計算量為2n,以此類推,本文算法m 迭代的計算量同樣為2n。也就是說本文算法的每次迭代的計算量與文獻[7]算法的計算量相同(除了第一次迭代),隨著迭代次數的增多,總的計算量二者基本相同。但是,本文算法采用階收斂的牛頓迭代方法,相同條件下,收斂時需要的迭代次數更少,因此在每次迭代計算量相同的條件下,本文算法從理論分析上來看需要的運算時間更短。
4 實驗結果與分析
為驗證本文所提出的算法有效性,采用概率密度分別為亞高斯分布、高斯分布、超高斯分布的信號作為信源信號,信源信號均值為0,方差為1。混合矩陣隨機產生。
圖1是5個信源信號,信號所有的采樣點均為5 000個點,但是由于采樣較多時隨機信號難以分辨,所以隨機信號僅畫出前500個采樣點。圖2是信源信號的混合信號。
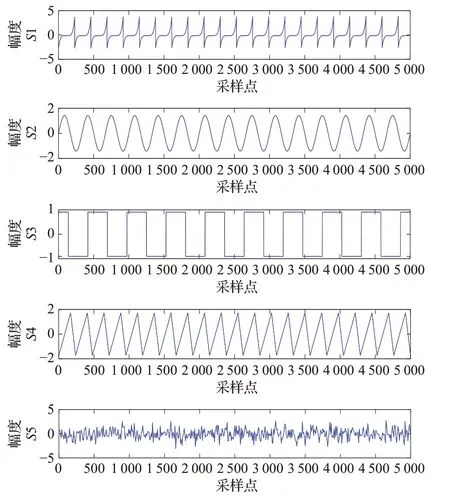
圖1 信源信號
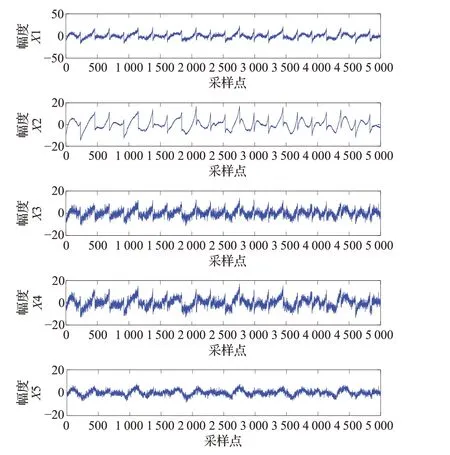
圖2 混合信號
圖3 是對圖1 信源信號S1 和S2 的估計;圖4 是對圖1信源信號S3、S4 和S5 的估計。
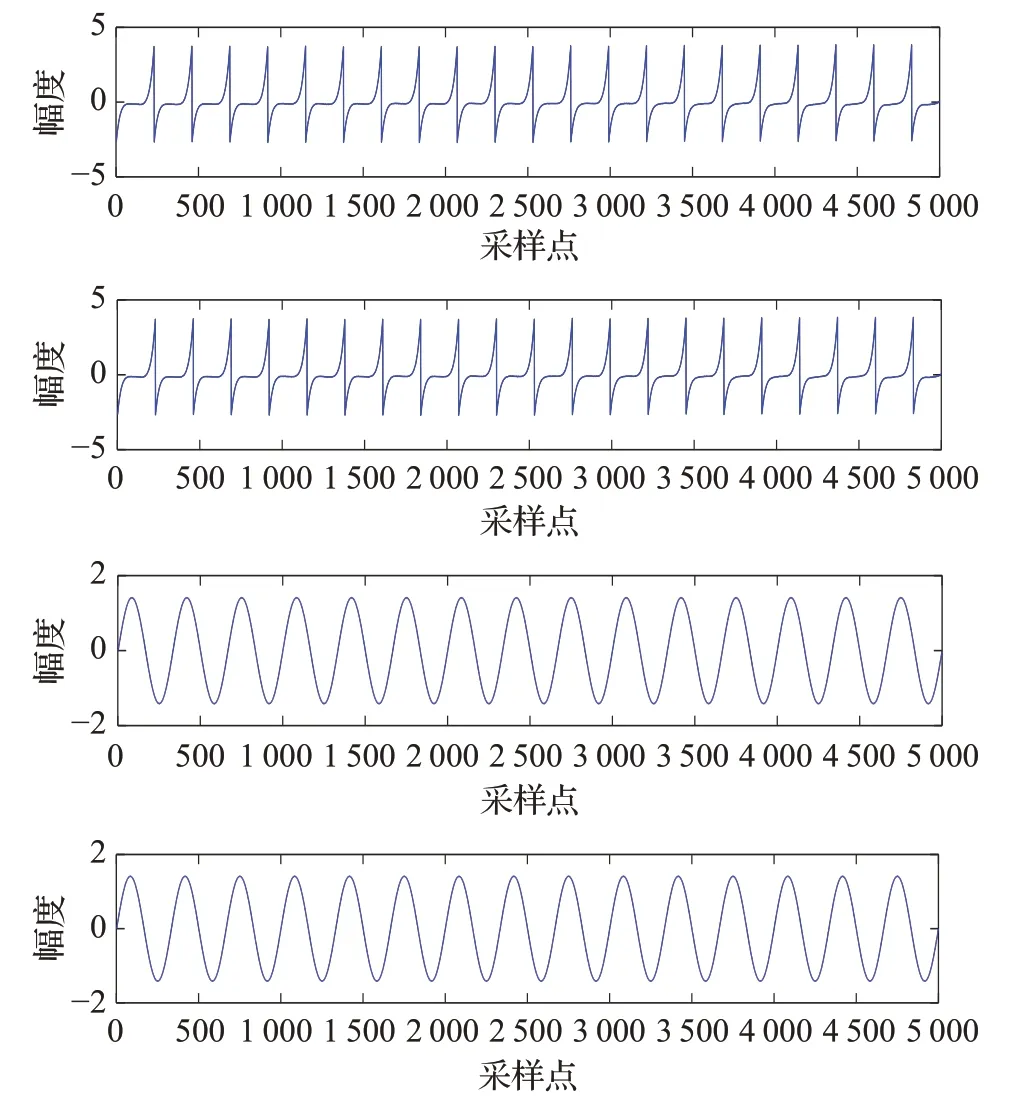
圖3 分離信號1
對比圖3、圖4 和圖1 可以看出,兩種算法都是有效的,都實現了對信源信號的估計。表1 給出了兩種算法的定量分析。誤差采用獨立分量分析中最為常用的性能指標函數進行度量,其具體表達式如(14)所示:
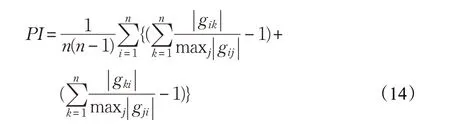
式中,g 代表的是分離矩陣與混合矩陣乘積得到的全局矩陣中的元素,n 時是全局矩陣的維度,理想條件下,性能指標為零,該指標的值越小,表示算法的誤差越小。從表1 可以看出,本文算法與文獻[7]算法性能指標一致,但是平均運行時間遠遠小于文獻[7]算法。
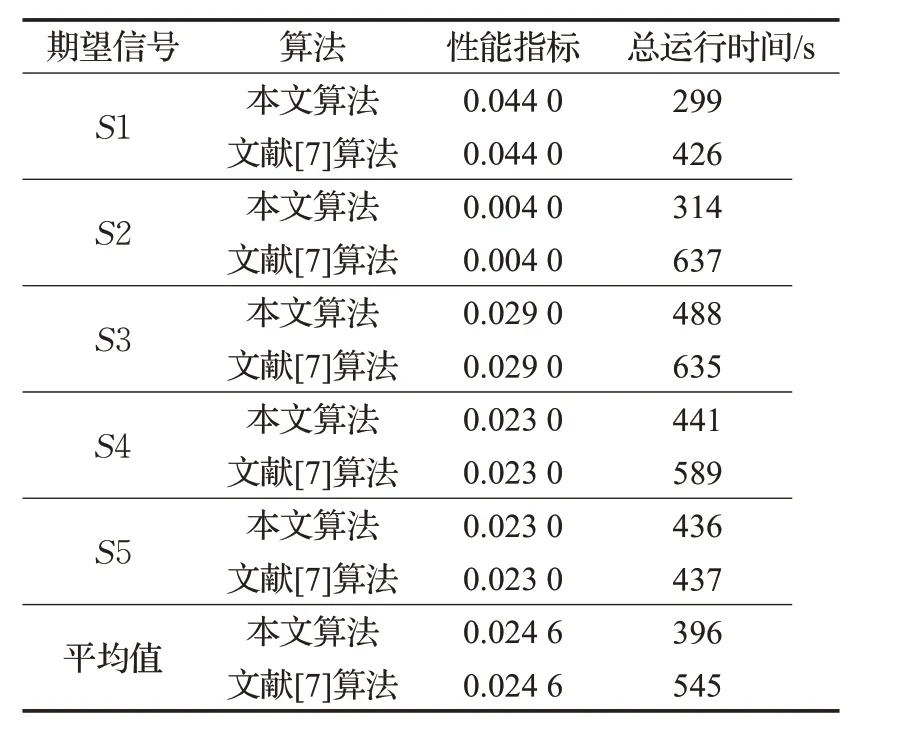
表1 算法平均性能分析
5 結束語
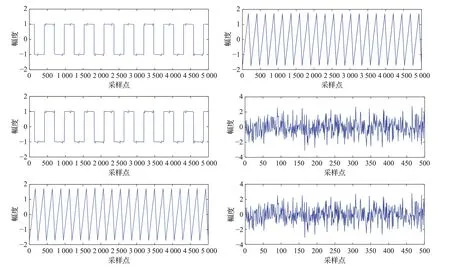
圖4 分離信號2
本文從參考獨立分量分析收斂速度角度出發,提出采用計算復雜度低、收斂階數較高的牛頓迭代方法對預處理后的混合信號的代價函數進行優化,推導出收斂速度更快的參考獨立分量分析方法。本文改進后的算法無論是提取亞高斯、高斯和超高斯信源信號都是有效的,而且相對已有方法的性能指標是相同的,但其收斂速度明顯快于已有方法。

