辨析題型結構 滲透轉化思想
——以一道初三數學試題為例

江蘇省蘇州市陽山實驗初級中學校 (215151) 尹國益

本文系蘇州市教育科學“十三五”規劃2019年度課題“發展初中生數學建模素養的教學實踐研究”(課題編號：192010343)的階段性成果.

一、選題背景

筆者作為初三的一線教師，一直著力研究如何提高學生中考的復習效率，思考如何從無限的題海中提煉出有限的題型，找到解題的策略與方法，從而減輕學生復習壓力，培養學生分析問題、解決問題的能力，提高他們的綜合素養.有一次，本人遇到了所在地區的一次期末考試題第28題，在閱卷和試卷講評中，發現學生存在以下問題：試題難度較高，很多學生不知道如何處理線段和的最值問題，找不到解題切入點；系數不為1的線段不會轉化，不能抓住一些細節，找不到解題的關鍵點；計算能力比較薄弱，很難抓住解題的得分點,等等諸如此類的很多.探究根源,其實質還是學生未能抓住題目的本質，未能把掌握試題的結構特征，未能找到與之相關的基本知識點.現將這類題型提煉出來，探索其解題思路，總結解決策略方法.

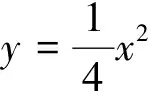
(1)求這條直線的函數表達式;

(2)在x軸上是否存在點C，使得ΔABC是直角三角形?若存在，求出點C的坐標，若不存在，請說明理由;

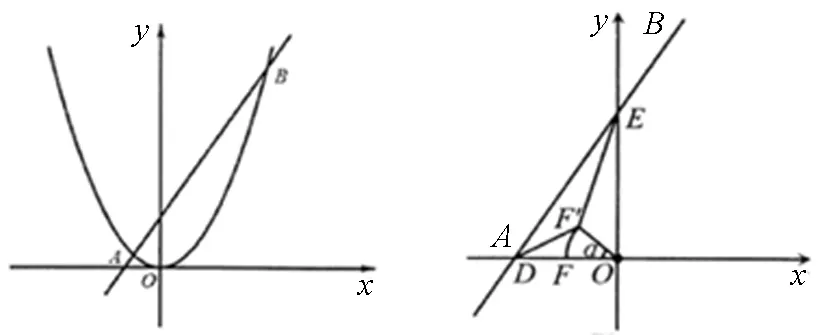
圖1 圖2

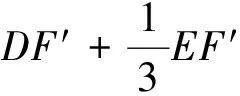
分析思考：第(1)問是輔助性試題，第二問是存在性問題都比較容易解決.筆者重點研究問題(3)的解決策略.問題(3)是線段和的最值問題，但又不是單純線段的和，(并不是所有線段的系數為1)簡稱″kAB+CD″型的最值問題，這類題型是中考常考查的題型，題型難度系數較高，題目閱讀量也比較大，里面牽涉的知識點也比較多.學生往往無從下手.如何處理這類問題?需要我們教師在平時教學中，一定要多帶領學生讀題審題，抓住試題的關鍵信息，把握題型特征，進行適當轉化，提煉出這類題型的解決策略.[2]這個過程不但可以探究這類題型的解法，更滲透了一些數學思想，從而進一步培養學生分析問題、解決問題的能力，提高他們的數學素養.

二、追根溯源

線段最值問題是平面幾何中比較經典的問題，要讓學生明白：從幾何角度處理線段最值問題，在初中階段有兩個基本知識點：一是兩點之間線段最短；二是直線外一點與直線上所有點的連線中，垂線段最短.兩個線段和的最值問題就可以優先利用上述知識點解決.

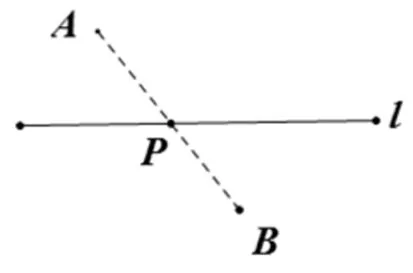
圖3

模型1(如圖3)在線段l上找點P，使得PA+PB最小.即當A、B、P三點共線時最小.(將軍飲馬問題)

模型2(如圖4)平面內一定點A，在線段m上找點P，過點P作PB⊥l于點B,使得PA+PB最小，即當A、B、P三點共線時最小.(胡不歸問題)

圖4

注：模型1是經典的將軍飲馬問題，兩個定點一動點，若A、B在l同側，還要利用對稱性，將同側轉化為異側，再借助兩點之間線段最短.模型2是胡不歸問題,雖然有兩個動點一個定點，但依據題目本身的特征，PB始終與l垂直，自然要利用垂線段最短原理.上述基本模型都是從兩個最短問題提煉出來的，共性都是求兩個有公共端點的線段和的最值問題，所求的都是“單純”兩個線段的和，(即每個線段系數都為1)，但遇到系數為k(k≠1)的線段，我們該如何轉化?這就是我們研究的主要內容.

三、解法探究

圖5

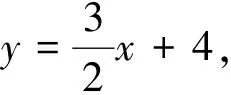
注：本題主要抓住對數據的處理與整合，構造了一個“反A字型”相似.將系數不為1的線段進行轉化，轉化成兩個有公共端點的單獨線段(系數為1)和的最值問題，再利用基本模型解決.在轉化時，一定要透徹地分析已知量，辨析題型的結構，把握其特征，找到轉化的路徑.但有時轉化不一定要用到相似形，還有一些其他方法，故找了一些對應的題型進行深度探究，提煉出解題方法與策略.

變式訓練：如何求3DF′+EF′的最小值？

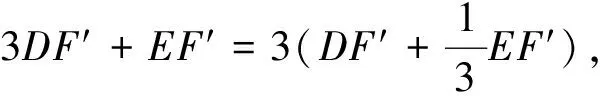
四、方法提煉

1.構造相似三角形

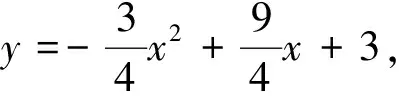
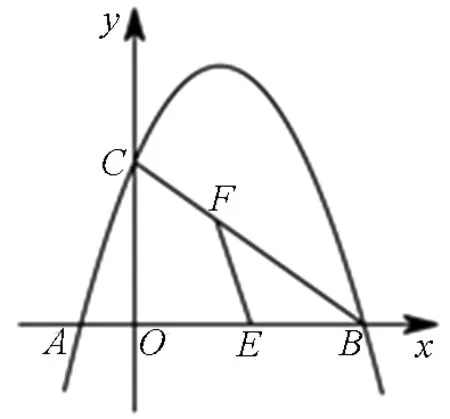
圖6

圖7

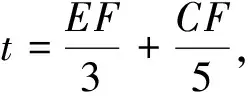
2.構造特殊角的三角函數值

圖8

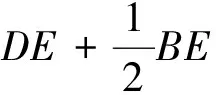
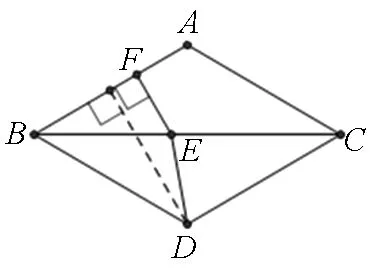
圖9

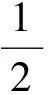
3.構造函數關系式

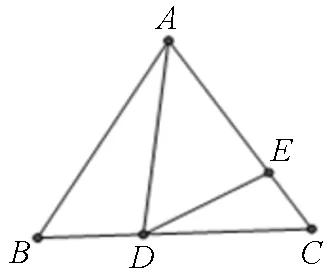
圖10

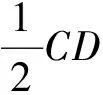
五、解題反思

本文主要探究了“kAB+CD”型的最值問題，雖然問題的背景在變，但解題的思想方法不變，重點是把握題型結構特征，將系數k進行轉化，通過構造相似形、特殊角的三角函數值，函數關系式等方法進行處理.因此，在平時解題教學中，教師一定要引導學生學會審題，結合已知條件辨析題型的特征，從宏觀上把握已知量和未知量內在的聯系，從而更容易探究解題方法.這正如波利亞曾說過，假如你想要從解題中得到最大的收獲，你就應當在所做的題目中去找出它的特征，那些特征在你以后求解其他問題時，能引起指引的作用.這要求我們教師在解題教學時要重過程、講方法，最好能提煉出一類題型的通解.

解題教學不光要教“解法”，更要教“想法”，因此在解題過程中，教師要回歸基礎，從學生掌握的基本圖形，基本技能出發，讓學生不斷地進行知識的遷移與建構，用他們已有的知識去解決新的問題，從而擴展他們的知識體系.在學生新知的建構過程中，教師要把握學生的思維方式，注重啟發學生的創造性思維，不斷地滲透題中所蘊含的數學思想,如轉化思想、模型思想、數形結合思想等.只有這樣，才能真正提高學生的解題能力和策略水平，才能達到“會一道”到“通一類”的突破，從而進一步提升學生的數學素養.