矩形小翼不同排列方式換熱特性研究

(華北理工大學 冶金與能源學院，河北 唐山 063210)

隨著時代的進步與發展,當今社會各種樣式的熱交換設備在建筑、能源、化學、金屬提煉、航天等工業方面大量使用。但傳統的換熱設備存在換熱效率較低，造成一定的資源浪費現象,只有逐步加強熱交換設備的使用效率,才能提高能源轉換效率，減輕能源浪費和材料短缺現象。因此，需要不斷開發出各種新的換熱方法實現熱交換效率的提高。

研究過程通過對湍流流動下流體在加裝矩形小翼的通道的流動的換熱特性開展模型設計及數值研究,比較矩形小翼在不同排列布置方式下不同的換熱特性,并提出換熱特性良好的攻角和排列方式,為矩形小翼在不同方式下的換熱特性的研究與技術的改良提供了一定量的數據參考。

1 物理模型的建立與數據處理

通過Gambit進行物理模型的建立，采用Fluent數值模擬進行計算，從而得到攻角對換熱性能的影響。研究過程中選擇順排、錯排、V形排列三種排列方式，截取通道的不同截面來研究相應的速度、溫度、壓力等云圖和流動軌跡圖，得出不同攻角下數據并作Nu-Re、f-Re、JF-Re折線圖研究討論，得到攻角對換熱性能的影響，并優化攻角的換熱。在不同的攻角中，選取換熱效果較好的角度，對其進行排列方式的優化，找出相同攻角下最佳的排列方式，選出較優秀的方案。

1.1 物理模型的建立

根據曾卓雄[2-5]等學者的研究發現，確定在60°時順排的換熱情況最佳，因此，研究過程首先進行大量研究在順排情況下，矩形小翼不同的角度排列的換熱情況，大致角度范圍定在30°～75°，每15°為一個單位量，如何進行驗證，并研究出在60°的情況下錯排、順排、V型排列那個更佳。大致確定的數據如表1所示。V形通道尺寸大致數據如表2所示，L、W、H為矩形通道的長、寬、高,m、n為橫、縱向間距，為攻角，l、w、h為矩形小翼的長、寬、高(其中a為兩對小翼之間的間距)。

表1 通道1基本數據

表2 通道2基本數據

1.2 數學模型

1.2.1 控制方程及邊界條件

(1)

動量方程：

(2)

能量方程：

(3)

方程的求解模型采用RNGk-ε湍流模型，用于確定湍動能k和湍動能耗散率ε的控制方程為[6]

(4)

(5)

式中：C1ε、C2ε、σε及σk為常數項；Gk表示平均速度梯度產生的湍流動能。此外，RNGk-ε模型中還引入了不同于標準k-ε模型的湍流黏度計算公式：

(6)

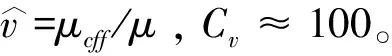
流經通道的干空氣密度ρ=946.2 kg/m3，黏度μ=2.19×10-5Pa·s，導熱系數λ=0.321 W/(m·K)，等壓比熱容cp=1 022 J/(kg·K)，水在圓管進口處的速度范圍定為3～10 m/s，有公式

(7)

式中：ρ為水的密度，g/m3；v為水在圓管進口處的速度,m/s；Dv為通道進口截面的當量直徑；μ為水的黏度[7]。

通過式(7)可得，不同速度下的雷諾數和湍流強度結果如表3所示。

表3 不同速度下的雷諾數和湍流強度

1.2.2 數據處理

雷諾數Re的定義為

(8)

式中：v為通道進口截面的平均速度；Dv為通道進口截面的當量直徑；μ為通道空氣的運動黏度。

通道壁面的局部表面傳熱系數定義如下

(9)

式中：qw為壁面局部熱流密度,kg/m3；Tw為壁面的溫度，K；Tf為冷卻氣體的平均溫度，K。

局部努賽爾特數Nux:

(10)

平均努賽爾特數Num:

(11)

換熱因子j定義為

(12)

阻力因子f定義為

(13)

式中：Δp為進出口壓差，Pa；L為通道長度，m；ρ為流體的密度，kg/m3。

綜合性能評價標準為

(14)

2 計算結果對比分析

2.1 攻角對流動換熱性能的影響

為了驗證所采用的數據模型可靠，分別從攻角、排列方式、兩個方面進行研究，研究各自對通道換熱性能的影響。首先，對攻角展開進一步的討論和流動傳熱的細節分析。由于物理模型在結構上的周期性重復，為了能夠展現局部并且節省計算空間只給出了兩排的小翼分布情況。

2.1.1 角度的優化

如圖1所示，由光滑通道與加裝矩形小翼的通道相比，加裝矩形小翼的通道的傳熱能力明顯提高，冷卻速度增加的區域主要為小翼周圍，可見矩形小翼區域的傳熱增強是由于小翼的阻擋帶來的特殊流動所改變的。因此分別選取加裝攻角為30°、45°、60°、65°、75°和90°的矩形小翼在通道內的計算結果進行對比分析。

圖1 矩形通道內的溫度變化

圖2為在順排的工況下，攻角為變化值，在攻角為30°、45°、60°、65°、75°、90°的通道的換熱面努塞爾數分布。由于攻角的度數不同使得換熱面積及傳熱系數發生了變化。6種通道在相同工況下的小翼表面的努塞爾數Nu/Nu0，如圖2所示。從圖2中可看出：30°、45°、60°、75°努塞爾數非常接近，攻角為60°、75°的通道努塞爾數大于其他2種，在雷諾數小于5 000時，攻角為60°時換熱效果最佳，當雷諾數大于5 000時，攻角為75° 的努塞爾數略大于攻角為60°，差值不超過2%。

圖2 相同工況下不同攻角下的通道換熱面Nu/Nu0分布

為了研究出矩形小翼綜合對流換熱流動性能相對較佳的攻角，進一步對矩形小翼攻角為90°時通道的換熱面努塞爾數進行求解，可以看出攻角為90°時換熱情況遠低于攻角為75°時，所以矩形小翼綜合對流換熱流動性能與攻角并非線性關系，加裝攻角為75°，在雷諾數大于5 000時矩形小翼綜合對流換熱流動性能相對較佳。

在進一步研究出矩形小翼綜合對流換熱流動性能相對較佳的攻角，進一步對矩形小翼攻角為65°時通道的換熱面努塞爾數進行求解。并對加裝攻角為65°的矩形小翼的矩形通道進行實驗分析。

如圖3所示阻力因子f反映的是矩形通道內的阻力特性，阻力因子的值越大，表面流體在流動過程中所消耗的功就更大。圖3所示為不同攻角的Re-f圖像，對不同攻角進行了比較。通過不同方式f的比較可看出，雖然攻角65°時的換熱性能表征系數Nu大于其他攻角度數，但其阻力因子并不是最小的，f的大小隨著攻角度數增大而增加明顯程度約為1%～5%。

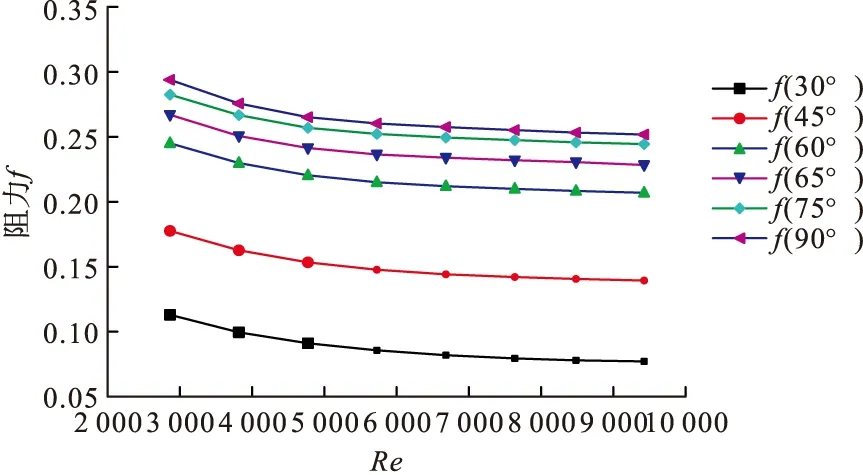
圖3 不同雷諾數下的阻力比較

當具有相同雷諾數時，換熱因子j和阻力因子f均隨著攻角的增大而增大，隨著雷諾數的增加而減小，最終都趨于穩定。不能判定哪種角度換熱效果最好，只能通過綜合性能來判斷，從圖4可以看出：綜合性能JF最好時對應的矩形小翼的攻角為65°。

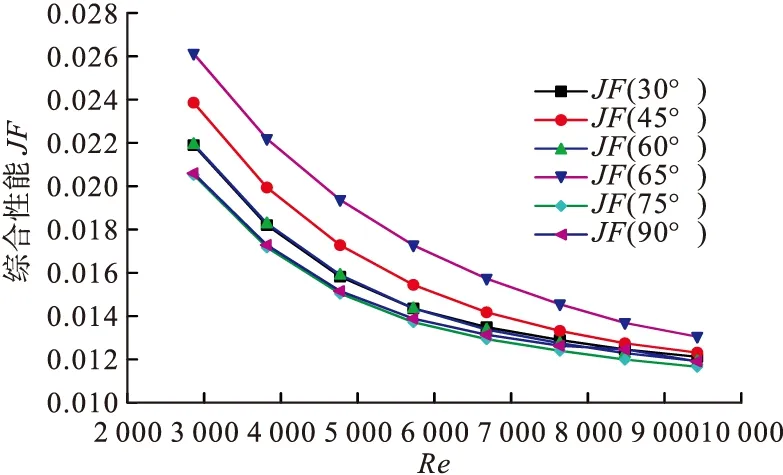
圖4 不同雷諾數下的綜合性能

得出如圖2所示結果，無論雷諾數為何值換熱,情況均好于60°和75°。且本身在不同雷諾數下呈線性增長趨勢，因此在相同工況下矩形小翼的攻角為65°時，換熱效果最佳。

2.1.2 速度場分析

圖5為速度在6 m/s時不同攻角下矩形小翼周圍的速度變化，由不同攻角的縱向截面速度矢量圖可以看出，隨著矩形小翼攻角的增大，小翼周圍的速度減小的面積區域越來越大，觀察圖5中的變化，小翼周圍的速度減小，說明流體流經通道受到了阻力的影響，且隨著攻角的變大，通道的阻力也增大。因此，加裝矩形小翼是阻力因子產生的原因。

圖5 不同攻角下的速度矢量圖

2.1.3 壓力場的分析

流體的入口速度為6 m/s的工況下，不同攻角下的壓力分布如圖6所示，圖中矩形截面左側為流體入口，右側為流體出口，觀察6種不同攻角下的壓力分布對比圖，根據整體的壓力分布圖可以看出：壓力的大小隨著流動方向而逐漸減小，進出口壓力的存在，是流體克服摩擦阻力進行流動的主要原因。不同攻角的壓力損失相比，攻角的增大會引起壓力損失的變大，也就是說都是由于流動阻力的增加而引起的。這說明傳熱性能的增強都是以流動阻力的增加而變化的。

圖6 不同攻角下的壓力云圖

2.2 排列方式對流動換熱性能的影響

2.2.1 排列方式的比較

圖7～圖9是不同攻角的矩形小翼在不同排列方式下的換熱情況，主要針對攻角為45°、60°、75°時的順排及錯排的流動換熱，得到的努塞爾數比Nu/Nu0(Nu0為光滑通道靜止時的努塞爾數)，通過折線圖可以得出：

(1)無論是何種攻角、何種排列方式下，當雷諾數不同時，努塞爾數比均大于1，說明不論在什么情況下，矩形小翼結構的引入使得通道換熱面Nu/Nu0明顯提高，小翼的強化傳熱效果明顯增強。隨著Re的增加,各種方案Nu/Nu0均近似線性增加。

(2)無論何種攻角，矩形小翼結構的引入使得通道換熱面Nu/Nu0明顯提高，小翼的強化傳熱效果明顯增強。隨著Re的增加,各種方案Nu/Nu0均近似線性增加；在Re相同時,順排小翼的Nu/Nu0相比于對應的錯排小翼傳熱效果明顯，差值不超過2%。

(3)兩種不同排列方式的換熱器綜合性能JF隨雷諾數的變化情況與基本結構相比有所降低，且隨著雷諾數的增加而減小，由于阻力的產生使加裝小翼的矩形通道換熱綜合性能比光滑通道要低。

圖7 相同工況下不同排列方式及不同攻角小翼通道換熱Nu/Nu0面分布

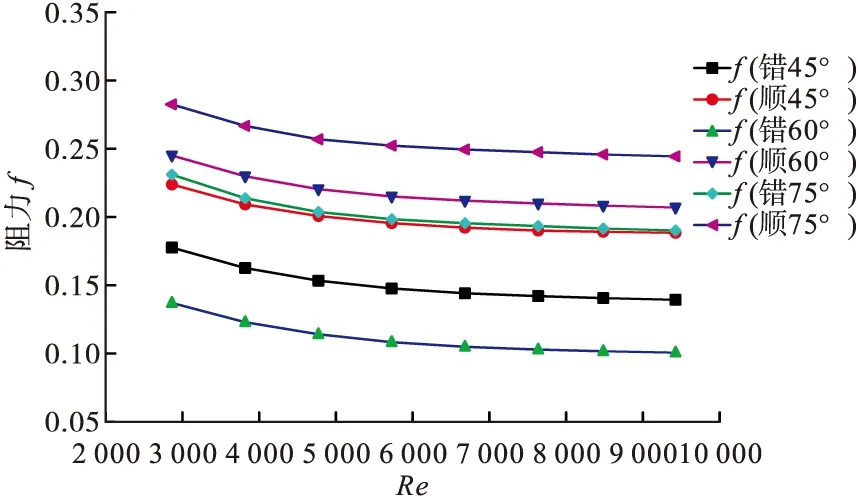
圖8 不同排列方式不同攻角的阻力比較

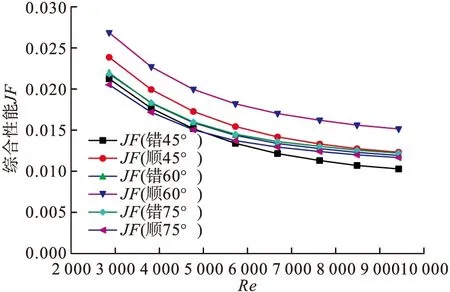
圖9 綜合換熱性能的比較

因此接下來在順排60°的相同條件下，采用不等間距(間距分別為25、35、45、55)的排列方式，來比較相同工況下的不同排列方式的換熱情況。得到數據如圖10所示。明顯不等間距排列方式的換熱情況優于錯排及順排。

其綜合性能同樣由換熱因子j及阻力f所決定，錯排、順排、不等間距排列的換熱因子基本相同，不等排列的在數值上稍微大一些，圖11表明三者的阻力系數卻是順排>不等間距>錯排，充分說明交錯排列所產生的阻力小，但換熱因子不如順排及不等排列，因此導致結果如圖12所示，不等間距排列的綜合換熱性能更好，雷諾數更高，換熱效果更優異。

圖10 相同工況下不同排列方式小翼通道換熱面Nu/Nu0分布

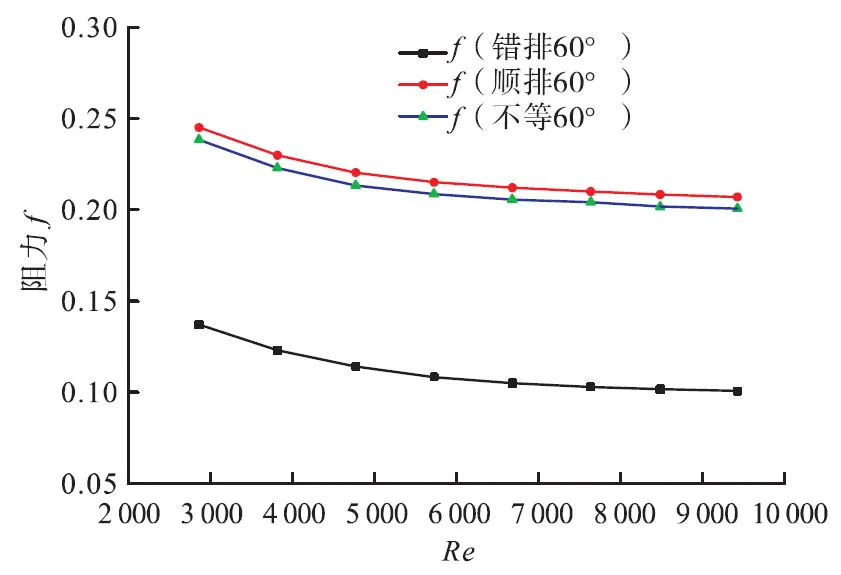
圖11 相同工況下不同排列方式的阻力

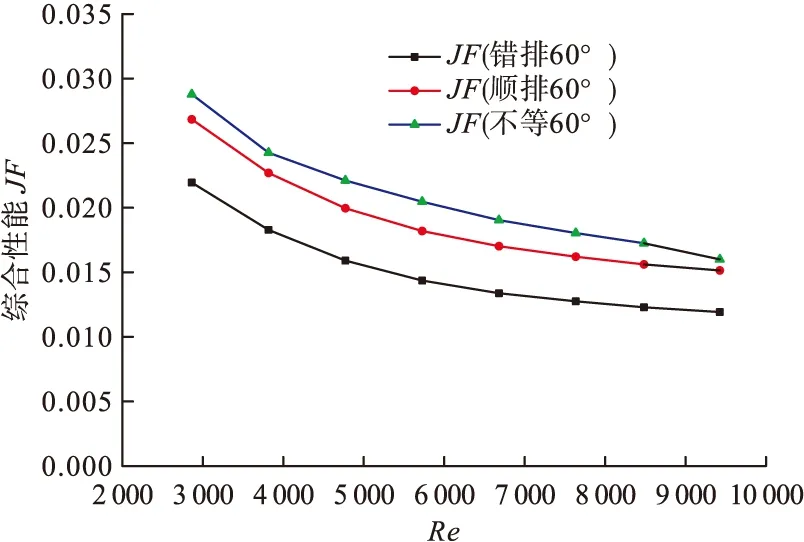
圖12 相同工況下不同排列方式的綜合換熱性能

為了比較V型排列與“一”字型排列的優越性，采用不同的模型，選取比較寬敞的通道進行V型排列，采用同樣介質流過通道，進行同樣的Fluent計算，得到圖13的結果。

圖13 相同工況下不同排列方式的阻力

如圖13所示，由于通道比較寬敞V型排列阻力相比于“一”字型排列阻力較低，如圖14所示，因此“一”字型排列的換熱情況要比V排列方式的換熱效果要好。“一”字形排列的努賽爾數高于V型1%。而圖15中綜合換熱性能兩種排列方式基本相同，差距很小。

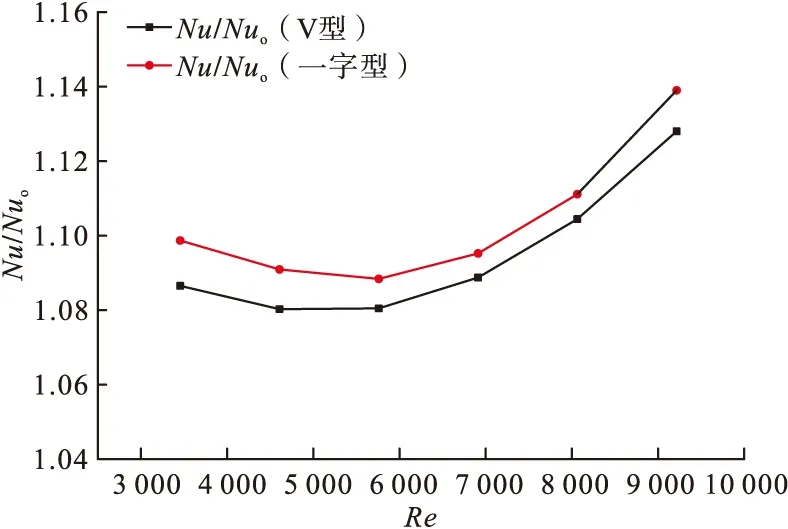
圖14 相同工況下不同排列方式小翼通道換熱面Nu/Nu0分布

圖15 相同工況下不同排列方式的綜合換熱性能

2.2.2 沿程分析

圖16給出了Re=5 727.3 ，矩形小翼個數為5對時，垂直于X軸方向截取210個截面(坐標分別為X1=-105、X2=-104、X3=-103……X108=103、X209=104、X210=105等截面)的努賽爾分布圖。由于進出口截面比較特殊，不放在計算結果內。

圖16 矩形通道的沿程Nu分布

由圖16可得，隨著流動的進行，橫截面上的溫度逐漸降低，而努賽爾數逐漸升高，但在升高的過程中流體被溫度較低的壁面小翼冷卻。在安裝矩形小翼的地方，由于矩形小翼的存在，產生一定的阻力而導致在小翼處的努賽爾增長緩慢，在小翼周圍努賽爾數先增加在減小，且增加的幅度越來越大，與光滑通道相比，加裝矩形小翼的通道沿程的換熱效果均比光滑通道高，結果如圖17所示。

圖17 沿程局部努賽爾數的對比

順排方式排列在坐標為0處是小翼的尾部，從圖17中可以看出，在流體通過效益的阻力后，努賽爾數迅速增加，一定距離后，努賽爾數開始逐漸降低，因此再來觀察錯排與順排相比。經過截面以及計算，得到結果如圖18所示。

順排時在0處有一對小翼，而錯排在0處只有單個小翼，經過小翼后順排的努賽爾數超過錯排的努賽爾數，其換熱情況反而超過了錯排方式，說明一對小翼所影響的換熱效果要比單個小翼的換熱效果好。

圖18 不同排列方式沿程的局部比較

2.2.3 溫度分析

在寬敞通道中，“一”字型排列的溫度變化與V型排列溫度變化相比溫差較明顯，出口溫度更低一些，因此換熱情況的比較中，“一”字型排列的努賽爾數更高(見圖19)。

3 結 論

研究應用Gambit及Fluent軟件對加裝矩形小翼的矩形通道內的流動換熱性能的影響進行了數值模擬分析，分別計算矩形小翼不同攻角和排列方式下矩形通道內的速度場、壓力場和溫度場。得到不同雷諾數下加裝矩形小翼矩形通道的阻力、換熱因子和換熱曲線，并比較分析了模擬和實驗的結果，驗證了模擬的可靠性主要從努塞爾數Nu、阻力因子f、換熱因子j及綜合換熱性能JF等性能系數進行換熱性能的分析，主要結論如下：

(1)具有矩形小翼的矩形通道流動和傳熱性是周期性波動的，在加裝矩形小翼的部分換熱能力最強，光滑部分換熱能力較弱，所以具有矩形小翼的矩形通道的換熱比光滑通道得換熱能力強。

(2)通過加裝不同攻角的矩形小翼的通道換熱情況對比，可發現：隨著矩形小翼攻角的增大，換熱通道的回流區面積逐漸減小。攻角為65° 的矩形通道，在不同的雷諾數下，努塞爾數呈線性增長，大于其它攻角下的努塞爾數，通道內的阻力隨著攻角的增大而增大，綜合換熱性能在攻角為65° 時呈現最佳狀態。

(3)在不同排列方式下，從數值模擬結果的觀察分析可得出，順排的換熱性能優于錯排，不等間距排列方式優于順排、錯排。

(4)寬敞的通道情況下，可以采用V 型排列與“一”字型排列方式的比較，研究表明，“一”字型排列的換熱情況優于V型排列。

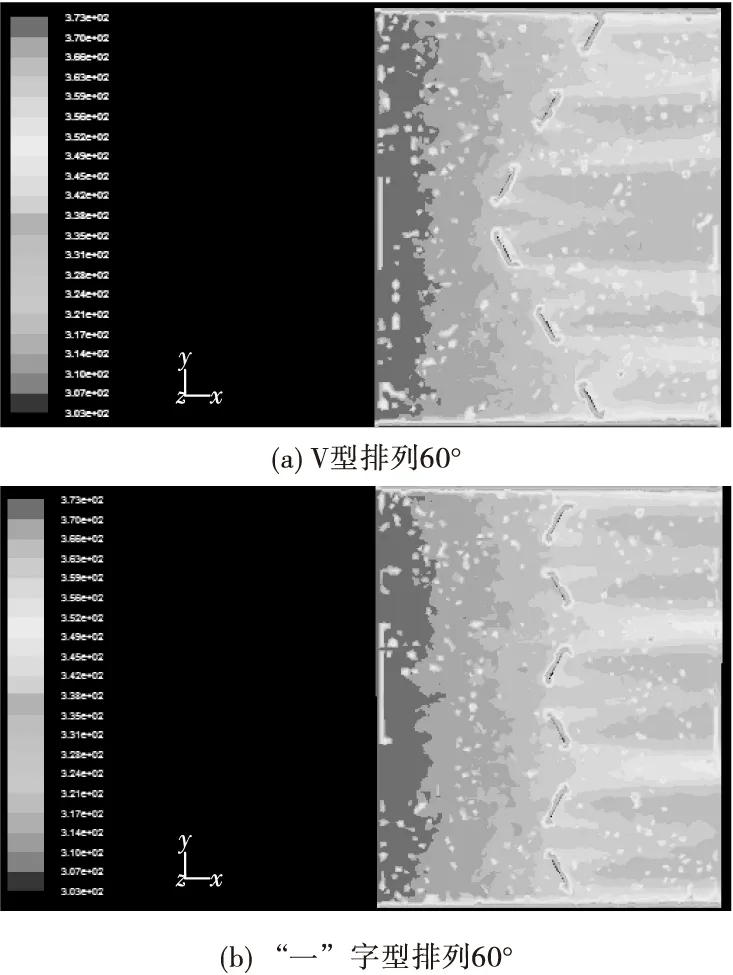
圖19 不同排列方式下的溫度變化