基于三方演化博弈模型的精準扶貧主體行為研究

□

[1. 三明學院 三明 365004；2. 電子科技大學 成都 611731；3. 廣西財經學院 南寧 530003]

引言

自2013年習近平總書記在湘西提出“精準扶貧”的概念以來，精準扶貧成為中國式扶貧的基本方略。國內外學者紛紛對此開展了大量的研究。2017年10月18日，黨的十九大報告強調指出，要動員全黨全國全社會的力量，堅持精準扶貧、精準脫貧。恰如阿瑪蒂亞·森指出的那樣，造成貧困的原因各異，但是，外部扶持力量對于貧困者逐步形成可行能力作用顯著[1]。他認為，能力的完備性取決于權力的可擴展性和可實現性。某種能力的缺乏導致了全面能力形成的障礙，突破障礙需要外在群體在權力分配和物質分配過程中的平等化救濟[2]。現有研究認為，貧困主體的解貧脫困離不開政府的主導扶助，作為準公共經濟活動，扶貧工作的開展更偏重于實現公平條件下，不同群體獲得共同發展的普惠福祉[3]。作為公共職能實施的主體，政府在政策制定、行動執行安排等協調性活動中作用顯著，但是，政府在資源創造、資金增值等經濟活動中作用不大，需要倚重企業的力量實現扶貧目標，增強減貧成效[4]。目前的文獻大體分為政府主導扶貧、社會力量參與扶貧、混合式扶貧等思路[5]。從研究者業已取得的成果分析，政府在調動社會力量積極參與扶貧的優勢無可比擬，但是扶貧工作既需要宏觀控制，又存在微觀行動支持和效果評價等具體實施過程[6]。增強貧困戶自我造血能力，需要社會力量在市場理念形成、產品風險規避、經營商品經驗方面加以引導[7]。科斯在論述企業的性質時，提出了企業在成長過程中，更重視成本降低帶來的效益提升，企業自利行為成為他們參與社會活動的重要動機[8]。因此，在準公共經濟活動中，保障企業在經濟活動中獲得穩定的直接收益和良好的社會聲譽產生的間接擴展性效益是促使企業投入到扶貧工作的基礎[9]。羅斯在肯定了阿瑪蒂亞·森的可行能力的公共特征后，進一步指出，政府在設定一定標準后，形成了社會群體認可的標準和可以達成共識的理念，是政治公正和正義得以量化的基礎[10]。政府扶貧政策實施、企業參與扶貧活動的最終效果都對貧困戶采取有限認知下的利益策略有重要的影響。羅斯試圖從打破個人差異性的視角說明公正性多數原則的合理性，但是，事實上，個體之間的差異會形成多方群體復制性共識，從而影響最終的政策效果。為此，降低不同個體差異性產生的效率損害的摩擦成本，減少目標偏離的可能性是實現政府、企業和貧困戶共同利益的基礎。和當前研究不同，本文將政府利益對策、企業自利行為對策和貧困戶個體差異對策進行了動態的演化分析，采用現場調查的數據和實際訪談的結果，模擬了現實狀況下不同利益相關者形成利益均衡的路徑。和現有的文獻研究相比，本文的貢獻在于更加客觀地從政府公共政策利益、企業在經濟發展和社會選擇均衡利益追求的平衡，以及個體差異性造成的決策變化這三方利益均衡的可實現性進行了模型的設定和模擬現實的效果展示，更加充分地展示了現有的扶貧工作中不同群體在目標達成中的演化過程，為打贏扶貧攻堅戰提供有益的參考。

為了減少現實因素的不確定性，設定三方群體的總目標保持一致，政府實施以提高人民生活水平為出發點的惠民政策，企業能夠在經濟利益和社會利益方面保持均衡策略，不會出現冒進等小概率事件，貧困戶以經濟利益為基礎考慮自身的決策。據上述的條件和相關的理論，提出以下模型，并做出了相應的假設。

一、基于政府、企業和貧困戶三方的演化博弈分析

（一）模型假設

精準扶貧過程涉及政府，企業和貧困戶三大利益相關者，三者之間存在相互博弈關系[11]。為進一步分析三個博弈主體之間的利益關系，尋求各方的利益均衡點，探索精準扶貧的有效途徑，需要構建精準扶貧三方利益主體演化博弈模型。

假設1：政府、企業和貧困戶是博弈的三大主體。三者在策略的選擇上均為有限理性，政府以社會福利最大化為目標，企業和貧困戶均以自身利益最大化為前提。本文僅從成本收益的角度出發，考慮政府如何用最少的成本達到最好的扶貧效果。三大主體中任何一方的決策取決于另外兩方的行為選擇。因此，研究三方之間的演化博弈有助于脫貧路徑的選擇。

假設2：參與策略。政府在精準扶貧過程中采取激勵與不激勵兩種行為，記為S1、S2；企業選擇介入和不介入兩種行為，記為E1、E2；貧困戶選擇積極脫貧和消極脫貧兩種行為，記為P1、P2。

假設3：當貧困戶的收入無法達到脫貧標準時，政府將采取兜底扶貧措施幫助貧困戶脫貧。

假設4：政府收益從其支付的扶貧資金的機會成本角度考慮。

假設5：根據三方主體選擇的策略，共可分為8種情形。

情境1：當政府不激勵、企業不介入、貧困戶消極脫貧時，即(S2，E2，P2)。企業的收益為E1；地方政府需要拿出扶貧資金資助貧困戶，收益為-K；貧困戶得到扶貧資金，最終收益為K（假定政府扶貧資金足以兜底所有的貧困戶）。

情境2：當政府不激勵、企業不介入、貧困戶積極脫貧時，即 (S2，E2，P1)。企業的收益為E1；地方政府需要拿出部分扶貧資金資助貧困戶，最終收益為W1-K；假定貧困戶積極脫貧的收入W1不能達到國定貧困線標準，政府會對貧困戶發放扶貧資金K-W1，此時，貧困戶的收入包括兩部分：貧困戶積極脫貧獲得的收入W1和政府的扶貧補貼K-W1，故貧困戶的最終收益為K。

情境3：當政府不激勵、企業介入、貧困戶消極脫貧時，即(S2，E1，P2)。企業要從總收益中拿出一部分扶持貧困戶，實際收益為E2-W2；由于貧困戶消極脫貧，企業扶持基金W2不足以脫貧，地方政府需要拿出扶貧資金資助貧困戶，地方政府的收益為W2-K；此時，貧困戶的收益包括政府扶貧資金K-W2和企業扶持資金W2，因此，最終收益為K。

情境4：當政府不激勵、企業介入、貧困戶積極脫貧時，即 (S2，E1，P1)。企業要拿出一部分的收益扶持貧困戶，收益為E2-W3；由于貧困戶積極脫貧，假定企業扶持基金W3足以使貧困戶脫貧（W3＞K），地方政府不需要拿出扶貧資金資助貧困戶，地方政府的收益為0 ；貧困戶得到扶貧資金，最終收益為W3。

情境5：當政府激勵、企業不介入、貧困戶消極脫貧時，即(S1，E2，P2)。企業的收益為E1；地方政府激勵貧困戶個體的成本為C1，同時需要拿出扶貧資金資助貧困戶，因此收益為-C1-K；貧困戶得到扶貧資金，最終收益為K。

情境6：當政府激勵、企業不介入、貧困戶積極脫貧時，即 (S1，E2，P1)。企業的收益為E1；地方政府需要拿出部分扶貧資金資助貧困戶，最終收益為W1′-K-C1；假定貧困戶積極脫貧的收入W1′不能達到國定貧困線標準，貧困戶的收益包含政府扶貧資金K-W1′和這種情境下貧困戶積極脫貧獲得的收入W1′兩部分，故此時貧困戶的最終收益為K。

情境7：當政府激勵、企業介入、貧困戶消極脫貧時，即 (S1，E1，P2)。企業的收益要拿出一部分扶持貧困戶，實際收益為C2+E2-W2′；由于貧困戶消極脫貧，企業扶持基金W2′不足以脫貧（W2′＜K），地方政府需要拿出扶貧資金資助貧困戶，地方政府的收益為W2′-K-C1-C2；貧困戶的收益包括獲得的政府扶貧資金K-W2′和從企業得到的扶持收入W2′兩部分，因此，貧困戶最終收益為K。

情境8：當政府激勵、企業介入、貧困戶積極脫貧時，即 (S1，E1，P1)。企業的收益要拿出一部分扶持貧困戶，實際獲得收益為C2+E2-W3′；由于貧困戶積極脫貧，假定企業扶持基金W3′足以使貧困戶脫貧（W3′＞K），地方政府不需要拿出扶貧資金資助貧困戶，地方政府的收益為-C1-C2；貧困戶得到扶貧資金，最終收益為W3′。

參數設置及含義如表1所列。

（二）模型構建

根據上述假設，可得到支付矩陣如表2所列。

假設政府選擇“激勵”策略的概率為x，選擇“不激勵”策略的概率為1-x；企業選擇“介入”策略的概率為y，選擇“不介入”策略的概率為1-y；貧困戶選擇“積極脫貧”策略的概率為z，選擇“消極脫貧”策略的概率為1-z。

表1 參數設置及含義

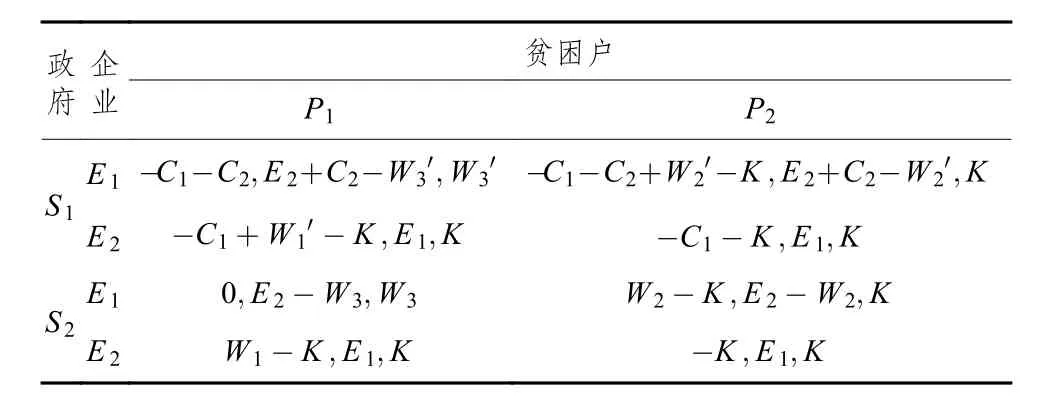
表2 支付矩陣

設US1表示政府采取激勵行為時的期望收益，US2表示政府采取不激勵行為時的期望收益，表示政府采取兩種策略時的平均收益，則：

同理，可得到博弈方企業采取合作行為的期望收益UE1和企業的平均收益分別為：

貧困戶采取積極脫貧行為的期望收益UP1和企業的平均收益分別為：

（三）結果討論

根據Malthusian動態方程，得出政府、企業和貧困戶之間的長期利益博弈行為和策略選擇隨時間演化的動力學方程。

考慮政府采取激勵行為的復制動態方程為

其中

考慮企業采取介入行為的復制動態方程為

其中

考慮脫貧戶采取積極脫貧行為的復制動態方程為

其中

設上述動力學方程的海瑟（Hessian）矩陣為：

（四）模型的漸進穩定性分析

二、案例分析與數值計算

通過查閱某個國家扶貧改革試驗區資料匯編和2016年某市精準扶貧第三方評估問卷調查數據統計資料，對各項參數測算結果如表3所示。

表3 某省某市某縣的扶貧數據 （單位：萬元）

（一）初始分布對演化路徑的影響

根據理論分析，政府、企業和貧困戶的初始狀態會影響演化路徑。將調查數據帶入復制子動態方程組中發現，對于固定的z，不論x和y取何值，復制動態方程F(x)和H(z)的符號不變，故政府和企業的初始狀態對演化路徑幾乎無影響。因此，本部分僅討論貧困戶的初始狀態z對演化路徑的影響。取x=0.5，y=0.5，演化結果如圖1和圖2所示。

由圖1可知，不論z取何值，系統演化到(0，0，1)的均衡狀態，即政府不激勵、企業不參與、貧困戶積極脫貧。顯然，該均衡狀態不是帕累托最優的。由圖2可知，z的不同取值對x演化到0的速度沒有太大的影響，不論貧困戶中積極脫貧的比例占多少，政府都采取不激勵策略。z較小時，y先增加后演化到0，并且z越小y增加的速度越大；z很大時（位于圖1中的陰影面以上），y呈減小趨勢，最終企業選擇不進入策略。初始z越大，其演化到1狀態也就越快，最終貧困戶都積極脫貧。

（二）政府兜底扶貧金額對演化路徑的影響

根據理論分析，政府兜底扶貧金額K會影響復制動態方程，從而影響演化均衡。本部分研究K對演化路徑和演化均衡策略的影響。為了便于研究，這里取x=0.5，y=0.5，z=0.5，K的不同取值為：K=200，300，400，500，600，700，800。演化結果如圖3和圖4所示。

由圖3可知，政府兜底扶貧金額K的不同取值會影響演化均衡結果，均衡結果包括三個(0，1，1)，(0，0，1)，(0，1，0)。具體演化結果可從圖4看出：1. 無論K取何值，x均演化到0狀態，即政府采取不激勵策略。2. 隨著K值變大，y從演化到0變化為演化到1狀態，即政府兜底扶貧金額變大時，企業介入扶貧可以降低扶貧成本因而選擇進入策略。3. 隨著K值變大，z從演化到1（當滿足本文假定的K＜W3時）變化為演化到0狀態（當K＞W3時），這是由于政府兜底扶貧金額過大導致貧困戶產生依賴政府脫貧的心理而選擇消極脫貧。因此，為了達到三個均衡點中的帕累托最優狀態(0，1，1)，K值不應過小，也不應過大，圖4中可知K=700左右可以達到該均衡。

（三）企業介入扶貧情況下企業的收益總額對演化路徑的影響

根據理論分析，企業介入扶貧情況下企業的收益總額E2會影響復制動態方程，從而影響演化均衡。本部分研究E2對演化路徑和演化均衡策略的影響。為了便于研究，這里取x=0.5，y=0.5，z=0.5，E2的不同取值為：200，400，600，800，1000，1200，1400。演化結果如圖5和圖6所示：

由圖5可知，企業介入扶貧情況下企業的收益總額E2的不同取值會影響演化均衡結果，最終導致均衡狀態下選擇積極脫貧的貧困戶比例不同。具體演化結果可從圖6看出：1. 無論E2取何值，x均演化到0狀態，即政府采取不激勵策略，隨著E2的增加，演化到0的速度也增加。2. 隨著E2值變大，y從演化到0變化為演化到1狀態，即企業介入扶貧情況下企業的收益總額E2較大時，企業因介入扶貧可以獲得收益而選擇進入策略。3. 隨著E2值變大，z從演化到非1狀態變化為演化到1狀態，這是由于企業介入扶貧給予貧困戶一定的就業機會和補貼。因此，為了達到帕累托最優狀態 (0，1，1)，企業介入扶貧情況下企業的收益總額E2要足夠大，由圖6中可知E2≥1000可以達到該均衡。

（四）W3對演化路徑的影響

根據理論分析，政府不激勵、企業介入、貧困戶積極脫貧情況下，貧困戶的收益W3會影響復制動態方程，從而影響演化均衡。本部分研究W3對演化路徑和演化均衡策略的影響。為了便于研究，這里取x=0.5，y=0.5，z=0.5，W3的不同取值300，400，500，600，700，800，900，1000。演化結果如圖7和圖8所示：

由圖7可知，政府不激勵、企業介入、貧困戶積極脫貧情況下，貧困戶的收益W3的不同取值會影響演化均衡結果，均衡結果包括三個(0，1，1)，(0，0，1)，(0，1，0)。具體演化結果可從圖8看出：1. 無論W3取何值，x均演化到0狀態，即政府采取不激勵策略，隨著W3的增加，演化到0的速度反而變慢，這是由于當企業介入時需要賦予貧困戶的收益W3較大，企業不愿意介入，導致政府考慮是否要采取激勵策略。2. 隨著W3值變大，y從演化到1變化為演化到0的狀態，即貧困戶的收益W3較大時，企業因介入扶貧需要付出較多的成本而選擇不進入策略。3. 隨著W3值變大，z從演化到0（當W3＜K時）變化為演化到1狀態（當滿足本文假定的W3＞K時），這時W3越大表明貧困戶可以獲得更多的收益。因此，為了達到上述三種均衡結果中的帕累托最優狀態 (0，1，1)，政府不激勵、企業介入、貧困戶積極脫貧情況下，貧困戶的收益W3不應過大，也不應過小，由圖8中可知400＜W3＜700可以達到該均衡。

三、結論

本文構建了精準扶貧過程中政府、企業和貧困戶三個利益相關者之間的演化博弈模型，分析了不同利益群體行為決策的演化趨勢，并通過數值仿真分析得到如下結果：1. 從實際調查數據可得，目前系統處于政府采取了大量激勵措施，企業參與扶貧程度參差不齊，貧困戶積極脫貧態度不夠明確的狀態。但通過模型分析，在現行政策引導下，經過長時間的演化，系統將最終達到(0，0，1)狀態，即政府不激勵、企業不進入、貧困戶積極脫貧。該狀態沒有實現帕累托最優。2. 導致系統無法達到帕累托最優的原因是多方面的，其中包括政府政策制定因素和市場因素。政策制定因素指的是政府兜底扶貧資金的設定，政府下撥和分配的扶貧資金規模應該適度，才能使系統達到帕累托最優。市場因素包括企業介入扶貧時所能夠獲得的收益以及貧困戶的人工成本。企業介入扶貧時所能夠獲得的收益回報越高越可能演化至帕累托最優。貧困戶本身積極脫貧時獲得的勞動報酬（即人工成本）適中合理時，有助于系統達到帕累托最優。

精準扶貧工作是一項范圍廣泛、投入巨大、情況復雜的系統工程，具有動態性、多維性、相對性和多樣性等特征，涉及眾多的相關利益群體[12]。而在本文的模型構建中只考慮了政府、企業和農戶三者之間的演化博弈關系，沒有考慮村集體等其他精準扶貧利益相關群體，因此，進一步探求精準扶貧過程不同主體的行為決策對扶貧成效的影響將是下一步研究的方向。