集成隨機配置網絡在養殖水質監測中的應用

李 康，王 魏，王奕鵬

集成隨機配置網絡在養殖水質監測中的應用

李 康，王 魏※，王奕鵬

（大連海洋大學信息工程學院，大連 116023）

為解決集約化水產養殖過程水體氨氮濃度無法實時檢測的問題，提出基于Bagging集成隨機配置網絡（stochastic configuration network，SCN）的建模方法，利用養殖過程采集的相關水質參數對養殖水體氨氮濃度進行軟測量。該方法首先采用Bootstrap方式生成多個不同的訓練子集，然后并行訓練多個SCN模型，最后將各個SCN模型的輸出結果取均值作為Bagging-SCN模型的輸出。為驗證方法的有效性，分別通過UCI標準數據庫中的機翼自噪聲數據集和集約化海水養殖過程數據集進行了仿真試驗，將該研究提出的Bagging-SCN模型與單一SCN模型、以及目前應用最廣泛的隨機權向量函數連接網絡（random vector functional-link net，RVFL）模型、Bagging-RVFL模型的測量效果進行了比較。試驗結果表明：該文所提模型對機翼自噪聲數據集中縮放聲壓級測量的均方根誤差、平均絕對百分比誤差和最大絕對誤差分別為4.225 dB、2.599 %和17.500 dB；在對集約化海水養殖過程中水體氨氮濃度測量的均方根誤差、平均絕對百分比誤差和最大絕對誤差分別為0.062 8 mg/L、27.851 mg/L和0.189 mg/L均優于其他測量模型；進一步說明該模型具有較高的測量精度和穩定性，更適合應用于集約化水產養殖水質監測過程。

軟測量；集成學習；隨機配置網絡；氨氮濃度；水質監測

0 引 言

在水產養殖過程中，氨氮濃度是衡量養殖水體水質的重要指標[1-3]。養殖水體氨氮濃度過高，不僅對水生生物的生存狀態造成巨大影響，還可能會對周邊的生態環境造成嚴重破壞[4-5]。近年來，隨著工業化、信息化技術的不斷進步，水產養殖模式也朝著集約化、精細化的方向發展[6-9]。良好的水質環境，是保證水產養殖收益的基礎，但高密度的養殖模式會加快養殖水質的惡化[10-11]，因此在集約化養殖過程中實現對養殖水體氨氮濃度的實時有效測量顯得尤為重要。

國內外學者利用數據驅動的軟測量建模方法，對水體氨氮濃度的測量進行了大量的研究。如高艷萍等[12]基于BP神經網絡對養殖水體氨氮濃度進行預測。Deng等[13]提出基于RBF的軟測量方法在線測量水體氨氮濃度。于輝輝[14]采用極限學習機對養殖水體氨氮濃度進行軟測量。喬俊飛等[15-16]分別基于RBF和遞歸RBF神經網絡對污水處理過程出水氨氮進行預測。這些方法很好的解決了傳統測量氨氮濃度（如納氏試劑法）存在的測量過程復雜、測量周期長、成本高等問題。然而，這些軟測量模型由于算法本身的局限性，很難實現快速高效的逼近性能，在處理大規模數據時具有一定的局限性。

近年來，隨著隨機權神經網絡的不斷發展，Wang等[17]提出的隨機配置網絡（stochastic con?guration network，SCN）由于其特有的學習機制，在快速學習的情況下，很好的保證了網絡較高的逼近性能，并因此得到了廣泛應用[18-22]。王魏等[23]采用SCN模型對養殖水體氨氮濃度進行預測，并得到較好的效果。然而，在SCN模型建立的過程中，網絡權重的隨機初始化以及網絡結構的不確定性會導致網絡輸出結果的不穩定。考慮到Bagging集成方法可以通過集成多個不同的子模型，在保證模型偏差不變的條件下，有效降低集成后模型的方差，進一步提高模型的泛化性能。因此，本研究提出基于Bagging集成的SCN建模方法，該方法首先利用Bootstrap的采樣方式生成多個不同的訓練集，然后基于不同的訓練集訓練生成不同的SCN模型，并將多個網絡模型進行集成，通過UCI標準數據庫中的機翼自噪聲數據集驗證了方法的有效性。最后，將所提模型應用于集約化養殖水體氨氮濃度的軟測量。試驗結果表明，該模型在測量水產養殖過程水體氨氮濃度時，不僅能夠提高氨氮濃度的測量精度，還具有較高的穩定性。

1 隨機配置網絡（SCN）算法概述

隨著工業信息化技術的不斷發展，數據規模的不斷增加，隨機權神經網絡在處理大規模數據時的有效性以及快速學習等優勢逐漸顯現[24]。與傳統梯度類神經網絡相比，隨機權神經網絡由于本身特有的學習方式，在保證模型逼近能力的情況下，很好的避免了網絡參數迭代調整的過程，大幅度提高了模型的學習效率，而且很好的克服傳統梯度類算法本身所固有的收斂速度慢，易陷入局部極小等問題，是近年來神經網絡領域一個重要的研究熱點[25]。然而，隨機權神經網絡在數據建模方面存在著一些問題。Tyukin等[26]通過實驗表明，當隨機參數的設置不合適時，隨機權向量函數連接網絡（random vector functional-link net，RVFL）不能以極高的概率逼近目標函數。Li等[27]揭示了增量式RVFL網絡的不可行性，并且Wang和Li[17]提出了一種基于監督機制的SCN模型，保證了隨機權神經網絡在數據建模時的通用逼近能力，其基本的網絡結構如圖1所示。

圖1 SCN基本網絡結構圖

SCN是一個典型的單隱含層前饋神經網絡，與傳統的單隱含層前饋神經網絡相比，SCN可在人為很少干預的情況下，從一個小型網絡開始，隨機的選取輸入權值和閾值，逐漸增加隱含層神經元節點的數量并利用最小二乘法求出輸出權值和偏置，直到網絡的訓練精度滿足終止條件。此外，SCN還針對隨機參數增加了不等式約束條件，根據隨機參數的大小，自適應的選擇隨機參數的取值范圍，進一步確保隨機化學習模型的通用逼近性[17]。

圖2 SCN算法基本流程圖

2 Bagging-SCN算法研究

集成學習是多種模型融合方法的統稱，通過構建并結合多個學習器來完成任務[28]。雖然集成學習的具體算法和策略各不相同，但都具有相同的基本步驟。首先生成一組相互獨立的基學習器，然后對基學習器進行訓練并按照某種結合策略將多個基學習器進行集成[29]。本研究采用集成學習方法中常見的Bagging并行集成方法，該方法由Breiman[30]于1996年提出，從一個給定的數據集中采用Bootstrap的方式采樣生成個樣本集，然后基于每一個樣本集訓練出一種基學習器，最后將這些基學習器進行集成。這種方式能夠降低模型輸出的方差，提高模型的泛化性能，且并行訓練的方式能節省大量的時間成本。

對于Bagging而言，基學習器的穩定性是能否有效提高模型性能的主要因素。要使模型通過Bagging集成后能夠大幅提高模型的測量精度和泛化性能，最重要的一點是要保證Bagging算法中基學習器之間具有一定的獨立性和差異性。由于SCN網絡對于訓練數據具有較強的逼近能力，其獨特的訓練方式給模型添加了不少的隨機性。采用Bootstrap方式進行采樣，使得不同的基學習器選用的訓練集樣本各不相同，進一步增加了SCN模型訓練時的差異性，從而提高了模型的泛化性能。因此，綜合2種算法的特點，提出基于Bagging-SCN的方法，流程如圖3所示。

圖3 Bagging-SCN基本流程圖

訓練集采用Bootstrap的方式進行采樣，生成個訓練子集，利用不同的訓練子集訓練生成不同的SCN模型，并將該子集中未被采集到的樣本作為各基學習器的驗證集，用于驗證各個模型性能。最后將所有基學習器的輸出取平均作為最終模型的輸出，利用測試集來對最終模型進行評估。算法步驟描述如下：

輸入：訓練樣本集、基學習器個數、基本SCN算法

輸出：集成學習器()

方法：

1）For=1 to

2）利用Bootstrap的方式從訓練集中有放回的抽取出與相同大小的訓練子集

3）基于不相同的訓練子集訓練對應的SCN算法，得到基學習器r()

4）End for

5）組合個SCN模型，輸出集成學習

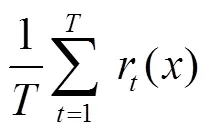
3 仿真試驗與結果分析

本部分主要對2個不同背景的數據集進行試驗。采用SCN、Bagging-SCN、RVFL以及Bagging-RVFL方法進行仿真，并通過均方根誤差（root mean square error，RMSE），平均絕對百分比誤差（mean absolute percentage error，MAPE），最大絕對誤差（maximum absolute error，MAE）3種不同的評價指標對上述不同模型的測量性能進行比較。

3.1 機翼自噪聲數據集仿真

3.1.1 數據描述

選用University of California Irvine（UCI）數據庫提供的機翼自噪聲[31]數據集。該數據集通過在消聲風洞中對二維和三維翼型葉片截面進行一系列空氣動力學和聲學測試獲得，共包含1 503個數據樣本，其中前5列作為網絡的輸入，分別是頻率、迎角、弦長、自由流速度、吸入側位移厚度，第6列為輸出，即縮放聲壓級，單位dB。本研究隨機取1 200個樣本作為訓練集，剩余303個樣本作為測試集，部分歷史數據如表1所示。

表1 機翼自噪聲部分歷史數據

3.1.2 仿真試驗

利用本研究所提方法建立Bagging-SCN模型來對縮放聲壓級進行測量，該模型每個基學習器SCN模型的訓練誤差與隱含層神經元的個數關系如圖4所示。

圖4 SCN節點個數與訓練誤差下降關系曲線

基學習器個數與模型輸出誤差下降的關系曲線圖，如圖5所示。隨著基學習器個數的增加，模型的輸出RMSE逐漸下降并趨于平緩。為了避免網絡模型過于復雜，本研究選取50個基學習器，其中每個基學習器的最大隱含層神經元個數為15，最大預選隱含層神經元個數為100，網絡每次遞增1個隱含層節點。Bagging-SCN模型對于機翼自噪聲數據的縮放聲壓級的測量效果如圖6所示。模型測量值與真實值關系的散點圖如圖7所示。

圖5 基學習器個數與誤差下降關系曲線

為驗證所提方法的有效性，在輸入特征數據與網絡最大隱含層神經元節點個數完全相同的條件下，將其測量效果與SCN、RVFL、Bagging-RVFL的測量效果進行對比，其中Bagging-RVFL模型中基學習器的個數也為50個。

圖6 Bagging-SCN模型測試結果曲線圖

圖7 Bagging-SCN測量值與真實值關系散點圖

為方便對比不同模型對機翼自噪聲數據的縮放聲壓級的測量效果，分別將Bagging-SCN模型，單一SCN模型，Bagging-RVFL模型以及單一RVFL模型對縮放聲壓級進行連續測量20次，統計各模型訓練和測試結果如表 2所示。

3.1.3 試驗結果分析

由表2可知，SCN模型的測量性能優于RVFL模型，Bagging-SCN和Bagging-RVFL 模型的訓練和測試效果在精度和穩定性方面優于單一模型，說明集成后的模型具有更好的性能。

3.2 養殖水質氨氮濃度軟測量仿真試驗

3.2.1 數據采集預處理

利用實驗室集約化循環養殖系統，以大菱鲆為養殖對象，通過養殖水箱安裝的不同水質參數傳感器采集數據，實現集約化養殖過程水質監測。基于王魏和郭戈[23]分析的結果，本研究將傳感器采集到的溶解氧、水溫、pH、電導率作為輔助變量，對氨氮濃度進行軟測量建模，它們與氨氮濃度之間的相關性大小分別為0.681、0.306、0.274、0.132。試驗采集到227組試驗數據，其中氨氮濃度由化學測試方式獲得。部分歷史數據如表3所示。由于采集到的不同特征對應的數據值差別較大，因此首先將數據進行歸一化處理，消除不同量綱對模型擬合效果的影響。

表2 縮放聲壓級測量結果比較

表3 所選水質參數的部分歷史數據

3.2.2 仿真試驗與結果分析

將采集到的數據進行預處理，隨機選取前150組數據作為訓練集，采用本研究提出的Bagging-SCN方法建立氨氮軟測量模型，并將剩余的77組數據作為測試集評估模型的測量性能。如圖8所示，為Bagging-SCN模型的水體氨氮濃度測量結果圖。為了驗證所提方法的有效性，將結果與單個SCN，Bagging-RVFL與單個RVFL網絡對養殖水體氨氮濃度的測量效果進行對比。各模型的參數設置與3.1節模型參數設置完全相同。

圖8 Bagging-SCN模型的氨氮濃度測量結果

同樣將各種算法進行連續20次測量，統計各模型的測量結果，如表4所示。

表4 氨氮濃度測量結果比較

觀察表4結果可知，單一的SCN比RVFL有較好的泛化性能，Bagging-RVFL比單一RVFL模型具有較高的測量精度和穩定性。與其他模型相比，Bagging-SCN模型的在測量集約化海水養殖水體氨氮濃度中具有最優的測量效果。

4 結 論

本研究利用Bagging集成算法能夠有效降低模型方差的優點，將其與SCN模型結合，提出基于Bagging-SCN的集成模型。該模型解決了SCN模型在建立過程中因網絡參數和結構的隨機化，致使模型測量性能不穩定的問題。通過UCI平臺的機翼自噪聲數據集驗證了所提模型的有效性。最后將該模型應用于集約化養殖水體氨氮濃度軟測量。通過對比單一SCN、RVFL和Bagging-RVFL、Bagging-SCN模型的測量效果，可知Bagging-SCN模型在測量養殖水體氨氮濃度時的均方根誤差和最大絕對誤差都較小，表明本研究所提Bagging-SCN模型進一步提高了集約化養殖水體氨氮濃度模型的泛化性和穩定性，對養殖水體監測具有一定的指導意義。

[1]陳英義，成艷君，楊玲，等. 基于改進深度信念網絡的池塘養殖水體氨氮預測模型研究[J]. 農業工程學報，2019，35(7)：195－202. Chen Yingyi, Cheng Yanjun, Yang Ling, et al. Prediction model of ammonia-nitrogen in pond aquaculture water based on improved multi-variable deep belief network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(7): 195－202. (in Chinese with English abstract)

[2]劉雙印. 基于計算智能的水產養殖水質預測預警方法研究[D]. 北京：中國農業大學，2014. Liu Shuangyin. Prediction and Early-Warning of Water Quality in Aquaculture Based on Computational Intelligence[D]. Beijing: China Agricultural University, 2014. (in Chinese with English abstract)

[3]李康，王魏，林少涵. 基于GA-SVR的海水養殖過程軟測量建模[J]. 控制工程，2019，26(11)：2047－2051. Li Kang, Wang Wei, Lin Shaohan. Soft sensor for intensive aquaculture process based on GA-SVR[J]. Control Engineering of China, 2019, 26(11): 2047－2051. (in Chinese with English abstract)

[4]蔡繼晗，沈奇宇，鄭向勇，等. 氨氮污染對水產養殖的危害及處理技術研究進展[J]. 浙江海洋學院學報：自然科學版，2010，29(2)：167－172，195. Cai Jihan, Shen Qiyu, Zheng Xiangyong, et al. Advancement in researches of ammonia pollution hazards on aquaculture and its treatment technology[J]. Journal of Zhejiang Ocean University (Natural Science), 2010, 29(2): 167－172, 195. (in Chinese with English abstract)

[5]張衛強，朱英. 養殖水體中氨氮的危害及其檢測方法研究進展[J] 環境衛生學雜志，2012，2(6)：324－327. Zhang Weiqiang, Zhu Ying. Advances on the research of the hazard of ammonia nitrogen in aquaculture water and its determination method[J]. Journal of Environmental Hygiene, 2012, 2(6): 324－327. (in Chinese with English abstract)

[6]Martins C I M, Eding E H, Verdegem, M C J, et al. New developments in recirculating aquaculture systems in Europe: A perspective on environmental sustainability[J]. Aquacultural Engineering, 2010, 43(3): 83－93.

[7]董雙林. 論我國水產養殖業生態集約化發展[J]. 中國漁業經濟，2015，33(5)：4－9. Dong Shuanglin. On the ecological intensification of aquaculture industry in China[J]. China Fisheries Economics. 2015, 33(5): 4－9. (in Chinese with English abstract)

[8]段青玲，劉怡然，張璐，等. 水產養殖大數據技術研究進展與發展趨勢分析[J]. 農業機械學報，2018，49(6)：1－16. Duan Qingling, Liu Yiran, Zhang Lu, et al. Analysis of research progress and development trend of big data technology in aquaculture[J]. Transactions of the Chinese Society for Agricultural Machinery. 2018, 49(6): 1－16. (in Chinese with English abstract)

[9]劉鷹. 海水工業化循環水養殖技術研究進展[J]. 中國農業科技導報，2011，13(5)：50－53. Liu Ying. Research progress on marine industrial recirculating aquaculture technology[J]. Journal of Agricultural Science and Technology, 2011, 13(5): 50－53. (in Chinese with English abstract)

[10]McKenzie D J, H?glund E, Dupont-Prinet A, et al. Effects of stocking density and sustained aerobic exercise on growth, energetics and welfare of rainbow trout[J]. Aquaculture, 2012, 216－222.

[11]高霄龍，劉鷹，李賢，等. 鮑放養密度對循環水養殖水質的影響及生物濾器凈化效果[J]. 農業工程學報，2017，33(21)：244－252. Gao Xiaolong, Liu Ying, Li Xian, et al. Effects of stocking density on water quality of Haliotis discus hannai Ino in recirculating aquaculture and purification effect of biofilter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 244－252. (in Chinese with English abstract)

[12]高艷萍，周敏，姜鳳嬌. 基于 BP 網絡養殖水體氨氮預測模型及實現[J]. 農機化研究，2008(7)：48－50. Gao Yanping, Zhou Min, Jiang Fengjiao. Prediction model and implementation of ammonia nitrogen in aquaculture water based on BP network[J]. Journal of Agricultural Mechanization Research, 2008(7): 48－50. (in Chinese with English abstract)

[13]Deng Changhui, Kong Deyan, Song Yanhong, et al. A soft-sensing approach to on-line predicting ammonia nitrogen based on RBF neural networks[C]. International Conferences on Embedded Software and Systems, 2009, 454－458.

[14]于輝輝. 基于機器學習的池塘養殖水質關鍵因子預測方法研究[D]. 北京：中國農業大學，2018. Yu Huihui. Prediction Research of Water Quality in Aquaculture Based on Machine Learning Method[D]. Beijing: China Agricultural University, 2018. (in Chinese with English abstract)

[15]喬俊飛，安茹，韓紅桂. 基于RBF神經網絡的出水氨氮預測研究[J]. 控制工程，2016，23(9)：1301－1305. Qiao Junfei, An Ru, Han Honggui. Water ammonia nitrogen prediction research based on RBF neural network[J]. Control Engineering of China, 2016, 23(9): 1301－1305. (in Chinese with English abstract)

[16]喬俊飛，馬士杰，許進超. 基于遞歸RBF神經網絡的出水氨氮預測研究[J]. 計算機與應用化學，2017，34(2)：145－151. Qiao Junfei, Ma Shijie, Xu Jinchao. Prediction of ammonia nitrogen based on recurrent RBF neural network[J]. Computers and Applied Chemistry, 2017, 34(2): 145－151. (in Chinese with English abstract)

[17]Wang Dianhui, Li Ming. Stochastic configuration networks: Fundamentals and algorithms[J]. IEEE Transactions On Cybernetics, 2017, 47(10): 3466－3479.

[18]王前進，楊春雨，馬小平，等. 基于隨機配置網絡的井下供給風量建模[J/OL]. 自動化學報，2019，1－12. Wang Qianjin, Yang Chunyu, Ma Xiaoping, et al. Underground airflow quantity modeling based on SCN[J/OL]. Acta Automatica Sinica, 2019, 1－12. https://doi.org/ 10.16383/j.aas.c190602. (in Chinese with English abstract)

[19]盛智勇，曾志強，曲洪權，等. 基于隨機配置網絡的光纖入侵信號識別算法[J]. 激光與光電子學進展，2019，56(14)：47－54. Sheng Zhiyong, Zeng Zhiqiang, Qu Hongquan, et al. Fiber intrusion signal recognition algorithm based on stochastic configuration network[J]. Laser and Optoelectronics Progress, 2019, 56(14): 47－54. (in Chinese with English abstract)

[20]Dai Wei, Li Depeng, Chen Qixin, et al. Data driven particle size estimation of hematite grinding process using stochastic configuration network with robust technique[J]. Journal of Central South University, 2019, 26(1): 43－62.

[21]代偉，李德鵬，楊春雨，等. 一種隨機配置網絡的模型與數據混合并行學習方法[J/OL]. 自動化學報，2019，1－12. Dai Wei, Li Depeng, Yang Chunyu, et al. A model and data hybrid parallel learning method for stochastic configuration networks[J/OL]. Acta Automatica Sinica, 2019, 1－12. https://doi.org/10.16383/j.aas.c190411. (in Chinese with English abstract)

[22]Li Ming, Wang Dianhui. 2-D stochastic configuration networks for image data analytics[J]. IEEE Transactions on Cybernetics, 2018, 1－14. https://arxiv.org/pdf/1809.02066v1.pdf

[23]王魏，郭戈. 基于隨機配置網絡的海水養殖氨氮濃度軟測量模型[J/OL]. 農業機械學報，2020，51(1)：214－220. Wang Wei, Guo Ge. Soft measurement model for ammonia nitrogen concentration in marine aquaculture based on stochastic configuration networks[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(1): 214－220. http://kns.cnki.net/kcms/detail/11.1964. S.20191112.0944.006.html. (in Chinese with English abstract)

[24]Scardapane S, Wang Dianhui. Randomness in neural networks: An overview[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2017, 7(2): e1200.

[25]喬俊飛，李凡軍，楊翠麗. 隨機權神經網絡研究現狀與展望[J]. 智能系統學報，2016，11(6)：758－767. Qiao Junfei, Li Fanjun, Yang Cuili. Review and prospect on neural networks with random weights[J]. CAAI Transactions on Intelligent Systems, 2016, 11(6): 758－767. (in Chinese with English abstract)

[26]Tyukin I Y, Prokhorov D V. Feasibility of random basis function approximators for modeling and control[C]. IEEE Control Applications (CCA) & Intelligent Control (ISIC), 2009, 1391－1396.

[27]Li Ming, Wang Dianhui. Insights into randomized algorithms for neural networks: Practical issues and common pitfalls[J]. Information Sciences, 2017, 382: 170－178.

[28]周志華. 機器學習[M]. 北京：清華大學出版社. 2016.

[29]諸葛越. 百面機器學習[M]. 北京：人民郵電出版社. 2018.

[30]Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123－140.

[31]Dua D, Graff C. UCI machine learning repository[J]. Irvine, CA: University of California, School of Information and Computer Science. 2019.

Application of ensemble stochastic configuration network in aquaculture water quality monitoring

Li Kang, Wang Wei※, Wang Yipeng

(,,116023,)

Ammonia nitrogen concentration is an important parameter to evaluate the quality of aquaculture water, and it determines the yield and benefits of intensive aquaculture production. In order to solve the problems of high cost, high consumption and difficulty in real-time and effective detection of ammonia nitrogen concentration, a method combining bagging ensemble algorithm and stochastic configuration network (SCN) which called Bagging-SCN were proposed. In this method, according to the current development of ammonia nitrogen measurement methods and random neural networks technology, SCN was chosen as the base learner due to its advantages of fast learning speed and strong ability to approach training data. The bagging ensemble method was used to integrate multiple networks, which effectively reduced the variance of the integrated model under the condition of keeping the model deviation unchanged. Specifically, the bootstrap method was used to generate multiple different training subsets for parallel training of multiple SCN models, and then different SCN models were generated by training with different subsets, and the uncollected samples in this subset were used as the verification set of each base SCN model to verify the performance of each model. Finally, the outputs of all base SCN models were averaged as the output of the final model, and the test set was used to evaluate the final model. In the modeling process of base learners, the SCN model started from a small network with little human intervention and randomly selected input weights and thresholds based on inequality constraints. It adaptively selected the value range of the random parameters according to the size of the random parameters to further ensure the universal approximation of the randomized learning model. The bagging method solved the problem that the randomization of network parameters and the uncertainty of network structure lead to the instability of measurement effect in the process of SCN modeling, and improved the measurement accuracy and stability of the model. To verify the validity of the proposed method, the experiments were mainly performed using two data sets with different backgrounds. The first experiment was based on the airfoil self-noise data set in the UCI standard database, and the frequency, angle of attack, chord length, free-stream velocity, and suction side displacement thickness was chosen as the auxiliary variables for modeling of scaled sound pressure level. The soft sensing modeling method of Bagging-SCN, SCN, random vector functional link net (RVFL) and Bagging-RVFL were carried out respectively based on the data set, for 20 consecutive times, and the output results of each model were statistically analyzed. These algorithms were verified by comparing the mean of the root mean square error (RMSE), the mean of the maximum absolute error (MAE) and the mean of the average absolute percentage error (MAPE) of the output predicted by different models, and the experimental results showed that the proposed Bagging-SCN model had a certain improvement in measurement accuracy and stability and had the best measurement performance compared with other models. The data set in the second experiment was collected by our laboratory intensive aquaculture system, and the proposed method was applied to the soft-sensing of ammonia-nitrogen concentration in intensive aquaculture. The relevant water quality parameters such as water temperature, pH, dissolved oxygen, conductivity which collected by sensors in the laboratory system were used as auxiliary variables for modeling of ammonia nitrogen concentration. Experiments with comparisons on the prediction effect of Bagging-SCN, SCN, Bagging-RVFL and RVFL models were carried out as the first experiment. Results indicated that the proposed algorithm had higher prediction accuracy and better generalization performance when measuring the ammonia nitrogen concentration in intensive aquaculture water. It had certain guiding significance for the monitoring of aquaculture water bodies.

soft sensing; ensemble learning; stochastic configuration network; ammonia nitrogen concentration;water quality monitoring

李 康，王 魏，王奕鵬. 集成隨機配置網絡在養殖水質監測中的應用[J]. 農業工程學報，2020，36(4)：220－226. doi：10.11975/j.issn.1002-6819.2020.04.026 http://www.tcsae.org

Li Kang, Wang Wei, Wang Yipeng. Application of ensemble stochastic configuration network in aquaculture water quality monitoring[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(4): 220－226. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.04.026 http://www.tcsae.org

2019-11-26

2020-01-15

國家自然科學基金（61503054）；大連市科技之星項目（2017RQ143）；遼寧省教育廳青年科技人才“育苗”項目（QL201912）

李 康，從事水質參數軟測量的研究。Email：1564028632@qq.com

王 魏，副教授，博士，從事復雜工業過程建模的研究。Email：ww_wangwei@dlou.edu.cn

10.11975/j.issn.1002-6819.2020.04.026

TP18

A

1002-6819(2020)-04-0220-07