基于ZEMAX二氧化硫熒光采集光路的設計仿真

劉杰輝，李 鑫

(河北工程大學 機械與裝備工程學院，邯鄲 056038)

引 言

迄今為止，空氣中二氧化硫的污染相對較為嚴重。人們在關注經濟快速發展的同時也開始注重環境的保護。為了更加準確地了解到我國現在環境的污染狀況,研制出能夠實時在線檢測的二氧化硫儀器勢在必行。二氧化硫檢測儀的原理是紫外熒光法，這是國家標準GB3095-2012中所規定的檢測方法。紫外熒光法可以突破傳統化學檢測方法的種種缺陷，能夠更準確地檢測二氧化硫[1]。其原理是：SO2氣體被波長范圍為220nm附近的紫外光照射時，SO2分子就從基態轉化為激發態，激發態的SO2是不穩定的，在其轉化為基態的時候產生熒光，對其產生的熒光進行收集利用就可以得出空氣中二氧化硫的含量[2]。熒光強度和光電倍增管輸出的電信號除去一些干擾以后是呈線性關系的。所以，對光電倍增管輸出的電信號進行一系列的放大、濾波等處理后，就可以得出二氧化硫的具體含量。紫外熒光法與傳統方法相比存在許多優勢，不僅能夠在線實時檢測，并且可以降低誤差，提高檢測的準確性。利用熒光光譜法對SO2含量進行檢測的過程中，最小的檢測范圍已經達到了10-9數量級[3]。

目前研發的二氧化硫檢測儀器采用的熒光采集光路是利用雙凸透鏡對熒光點光源進行了匯聚。該系統存在很多不足，不僅光線的匯聚效果不理想、存在較大像差,而且由于透鏡的焦距長導致增大了熒光采集光路的長度[4]。基于上述光路的種種缺陷，本文中提出了一種新型對稱式平凸結構，可以有效解決上述光路存在的問題，并通過ZEMAX仿真驗證了對稱式平凸結構的合理性。

1 理論依據

在實際運用中幾乎不可能達到完美的成像質量。由球差效果圖可知，光線并不在光軸上聚于同一個焦點，而在鏡頭邊緣入射的光線與光軸的交點要比接近光軸入射的光線與光軸的交點離鏡頭的距離近，如圖1所示。這是很常見的像差之一，稱之為球差[5]。球差的大小取決于光線在入瞳上的高度。消除球差可以采用非球面，非球面雖然不能完全消除像差，但可以使像差達到最小[6]。減小球差的另外一個方法是將光焦度進行分解[7]。

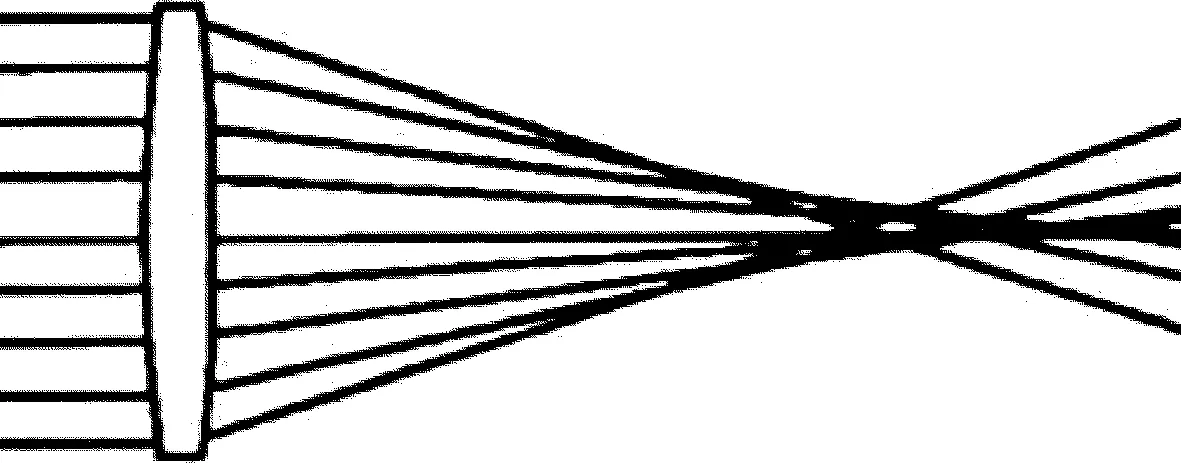
Fig.1 Effect of spherical aberration

1.1 非球面消球差

在光學系統中，想要將球差減小到最小，首先應該明白球差產生的原因是什么。從理論上來說，如果一個系統中不存在球差，那么系統中任意光線的光程是永遠相等的。

在建模過程中首先需要建立一個適當的坐標系。在光學系統中，取其中一條單面子午截線的對稱中心作為原點建立直角坐標系。所以，無限遠處的點光源發出的平行光照經過該系統后，選取經過單面子午截線上點P(x，y)的遠軸光線和近軸光線作為研究對象，如圖2所示。按照上述理論可知，近軸光線和遠軸光線的光程應該相等。遠軸光線經過點P(x，y)交x軸于點b，交y軸于點a，近軸光線是與x軸重合的光線，與遠軸光線共同交于點b；n和n′分別代表的是空氣的折射率和光學系統的折射率；xP和yP也就是P點的坐標值；f′是近軸光線經過的路程。對于任意一個給定的光學系統，如果這個系統不存在球差，那么一切經過這個特定光學系統的光線都應該在光軸上交于同一個點。也就是說，這兩條光線的光程是恒等的。遠軸光線光程的具體公式是：

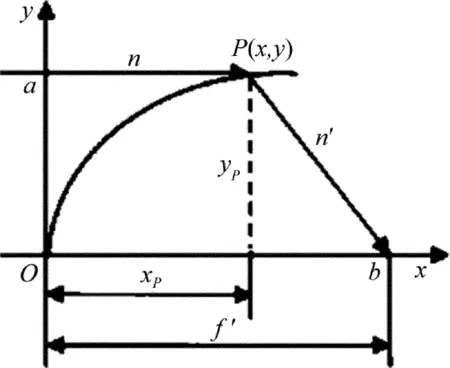
Fig.2 Imaging of infinite object point due to single refractive surface

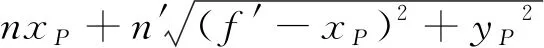
(1)

近軸光線光程則為n′f′，因此對于任意子午截線上的點，光程恒等的曲面是：

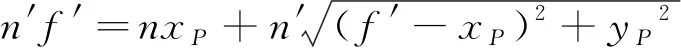
(2)

化簡得:

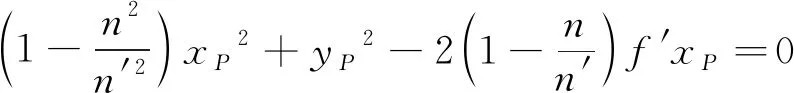
(3)

由(3)式可得：當f′一定時,n′>n為橢圓；n′/n=-1為拋物面；n′/n=1為平面(yP=0)。

除去n′/n=-1的情況后，該方程仍然是二次的，所研究的光路系統n和n′分別代表空氣和石英的折射率，所以不符合上述條件。即將球面透鏡非球面化以后可以達到消球差的目的。

非球面上各個點的曲率半徑均不相同，其面形由高次多項式決定。從光學角度而言，非球面指折射面為球面以外的所有面。設計者可以通過改變其曲率來獲得理想的成像質量。

1.2 雙球面折射系統光焦度

圖3為雙球面折射系統圖。圖中,u1表示入射張角，u2表示出射張角，h為光學系統入射點到主軸的距離，n1，n2和n3分別表示不同介質的折射率。由圖3可知，雙球面系統光焦度F的表達式為：

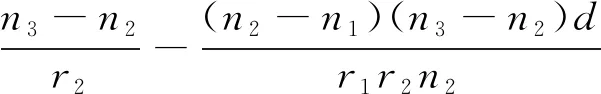
(4)

式中,O1折射面的光焦度為F1,O2折射面的光焦度為F2；d為兩個折射面之間的距離；r為曲率半徑，光從左向右傳播，以球面和主光軸的交點為準，球面的球心在該點以左，則曲率半徑為負，反之，球心在在該點以右，則曲率半徑為正。r1為第1個折射面的曲率半徑，r2為第2個折射面的曲率半徑。

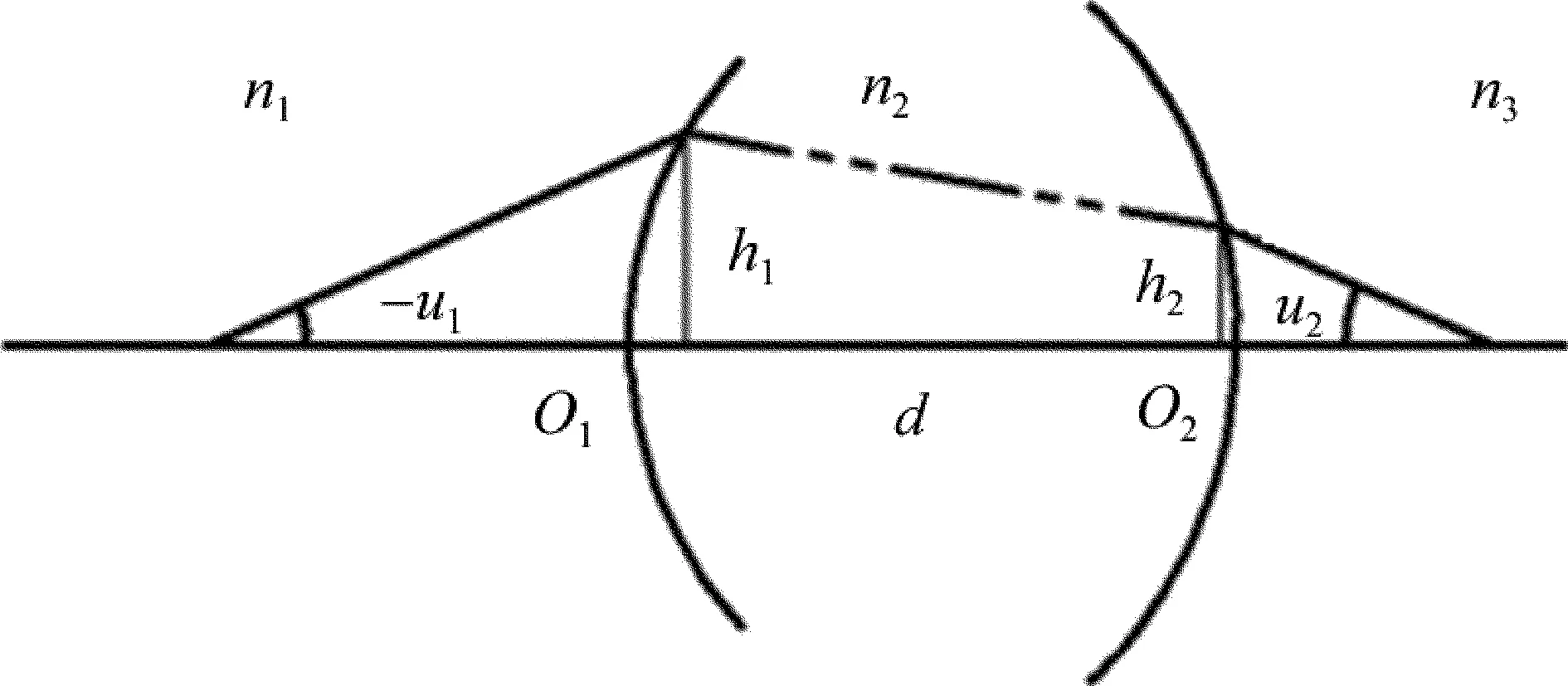
Fig.3 Bispherical refraction system

如果是雙凸透鏡系統，石英透鏡的折射率要大于空氣折射率，則n1=n3代表空氣中的折射率；n2表示石英透鏡的折射率；曲率半徑r1=-r2，且r1>0,那么化簡可得：

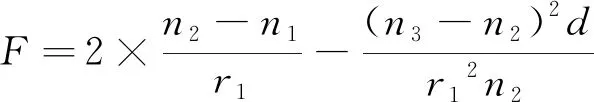
(5)

同理,如果是對稱式平凸透鏡，則n1=n3代表石英透鏡的折射率；n2表示空氣的折射率；曲率半徑r1=-r2，且r2>0,化簡得：

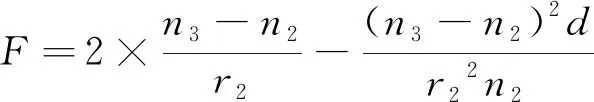
(6)

由于兩個光路都對光線進行了匯聚，所以光焦度F的值應該大于0。在本次設計過程中，對稱式平凸透鏡和雙凸透鏡的曲率半徑相同；材料和波長相同，所以空氣和石英透鏡的折射率是相同的；雙凸透鏡的d值明顯大于對稱式平凸透鏡的d值，所以F對稱式平凸>F雙凸。由理論可知，在光焦度大于0的情況下，F的值越大，匯聚效果越好。

因為非球面價格昂貴、沒有足夠的精度以及隨溫度變化的不穩定性，故其在實際領域里難以普及。所以減少像差可以在光學系統中增加光學元件，光焦度可以在幾個元件間進行分解，這樣可以降低每個表面上的入射角度，從而達到的目的。

2 ZEMAX優化仿真分析對比

2.1 光路對比

目前的二氧化硫監測儀器采用一個雙凸透鏡和一個濾光片組成熒光采集光路，如圖4所示。由熒光發出的點光源經過雙凸透鏡進行匯聚，在通過濾光片濾光后入射到探測器上。為了減少像差而采用的對稱式平凸結構，在兩個透鏡中設有可以限制較大入射角光線的隔鏡環，在探測器前面設有濾光片，如圖5 所示。將以上兩種光路運用ZEMAX仿真進行對比。

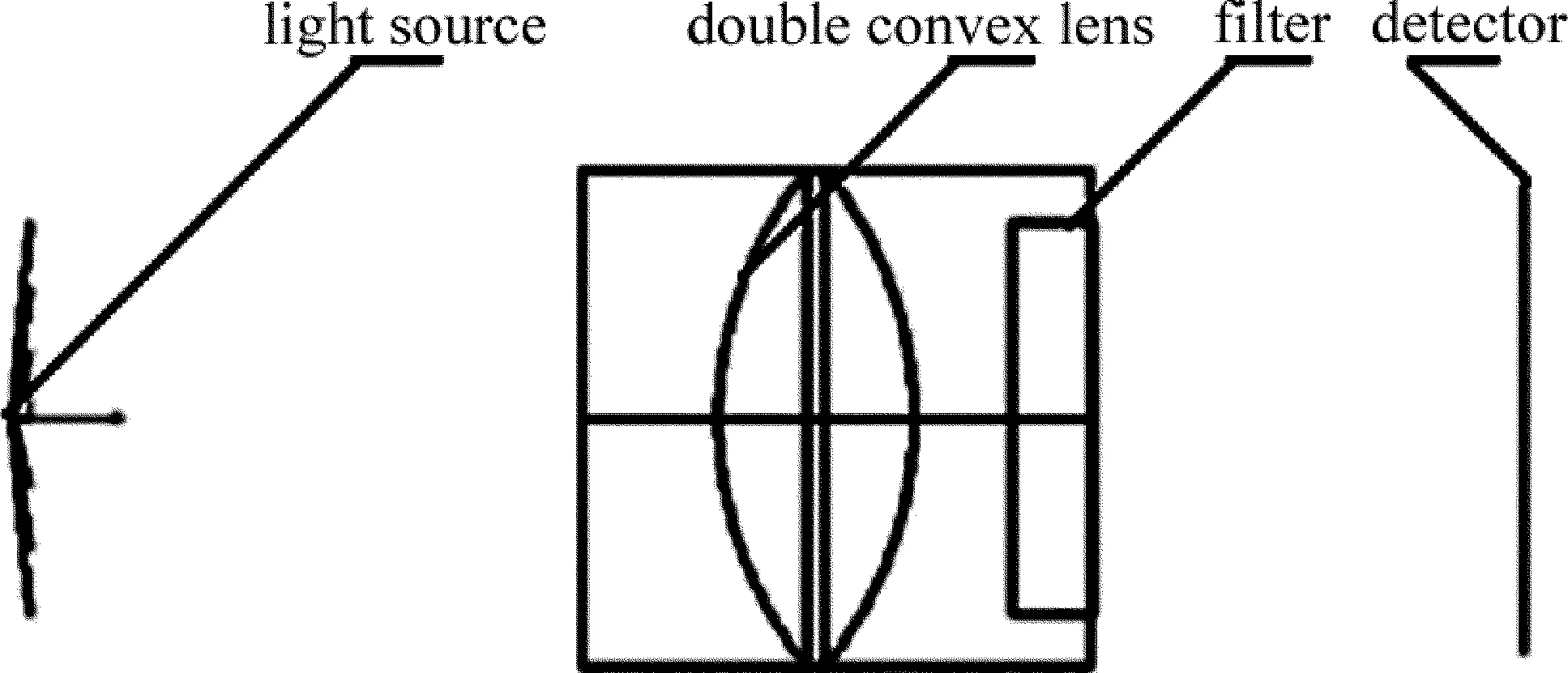
Fig.4 Fluorescence acquisition system with dual convex lens

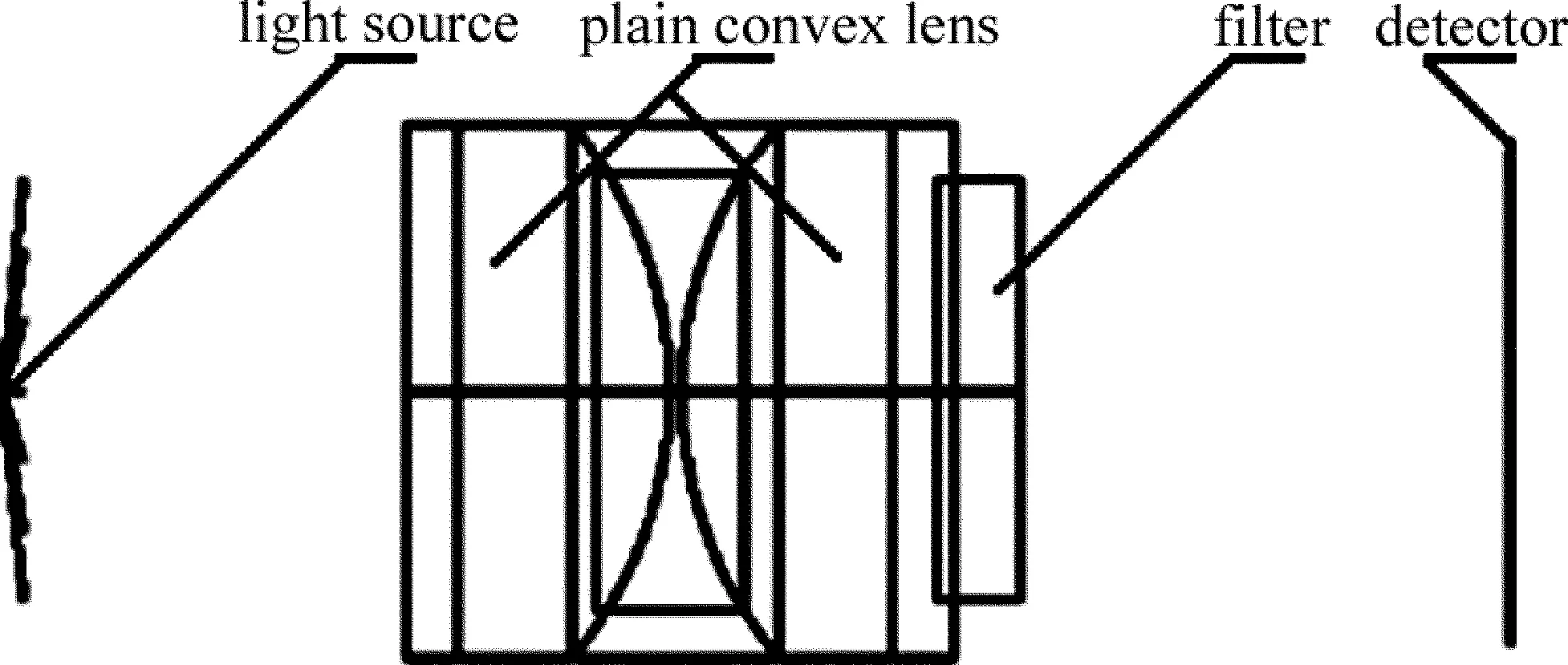
Fig.5 Acquisition system with symmetrical plano-convex lens

2.2 仿真及優化

設計或者優化任何一個光路結構，都有特定的要求，例如焦距、入瞳直徑、視場、波長、材料、分辨率、漸暈和調制傳遞函數(modulation transfer function,MTF)等，根據不同系統的簡易程度要求也各不相同[8]。由于熒光波段在330nm強度最高，所以設定的波長是330nm；在240nm～420nm的波長范圍內，石英透鏡對二氧化硫發射出熒光的透過率比普通玻璃透鏡大很多，所以材料選用石英玻璃；其中視場為1，入瞳直徑為20mm，分辨率為2048×2048。

在確定光路的具體路徑后對兩個光路進行局部優化，得到最小的光斑半徑。ZEMAX中局部優化算法有阻尼最小二乘法(damped least squares,DLS)和正交法(orthogonal descent,OD)，在純非序列系統中由于探測結果是在被像素化的探測器上獲得，其評價函數是不連續的，使用阻尼最小二乘法的運用效果并不理想，故采用正交法更為合適。

正交法對變量進行標準化，并對解空間進行離散化抽樣來降低評價函數，并不計算評價函數的數值導數。相比較于阻尼最小二乘法，正交法對含有噪聲評價系統的函數(比如非系列系統)更有優勢。正交法能夠很好的完成照度最大化、亮度增強以及均勻化的優化問題。圖6即為采用正交法后的優化結果。可以看到，將光斑半徑明顯減少達到了預期的優化效果。

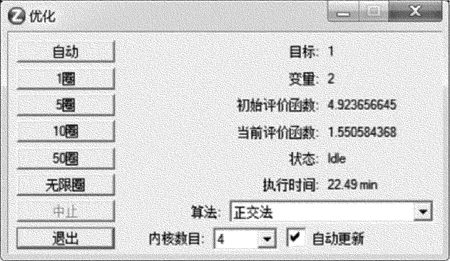
Fig.6 Orthogonal optimization diagram

2.3 仿真結果分析對比

以下是運用ZEMAX對兩種光學系統進行仿真優化后的具體對比。

(1)首先進行兩種系統的光路仿真，光線從光源發出經過透鏡后匯聚于探測器上，如圖7和圖8所示。對比兩種光路的非序列結構(non-sequential compoonent,NSC)陰影模型圖，觀察到圖7中經過對稱式雙凸透鏡入射到探測器上的光線較圖8中雙凸透鏡的匯聚效果更加集中，光線散射程度更小。對稱式雙凸透鏡光路設計更加合理。

Fig.7 NSC shadow model diagram of double convex lens

Fig.8 NSC shadow model diagram of symmetrical plano-convex lens

(2)為了更好地比較兩種光路匯聚效果，設置光線條數為1000，跟蹤分析光線探測器，得到探測器視圖，如圖9和圖10所示。對比兩種光路的峰輻強度、總功率以及撞擊次數(見表1)[9]，發現優化后的峰輻強度達到了219.41W/cm2,是之前的3倍，總功率達到了0.35410W。由此可見，對稱式平凸透鏡的匯聚效果要比雙凸透鏡的匯聚效果好,即在相同的熒光強度下，對稱式平凸透鏡可以更好地進行匯聚，以便于接收器接收到更多的信號[10]。

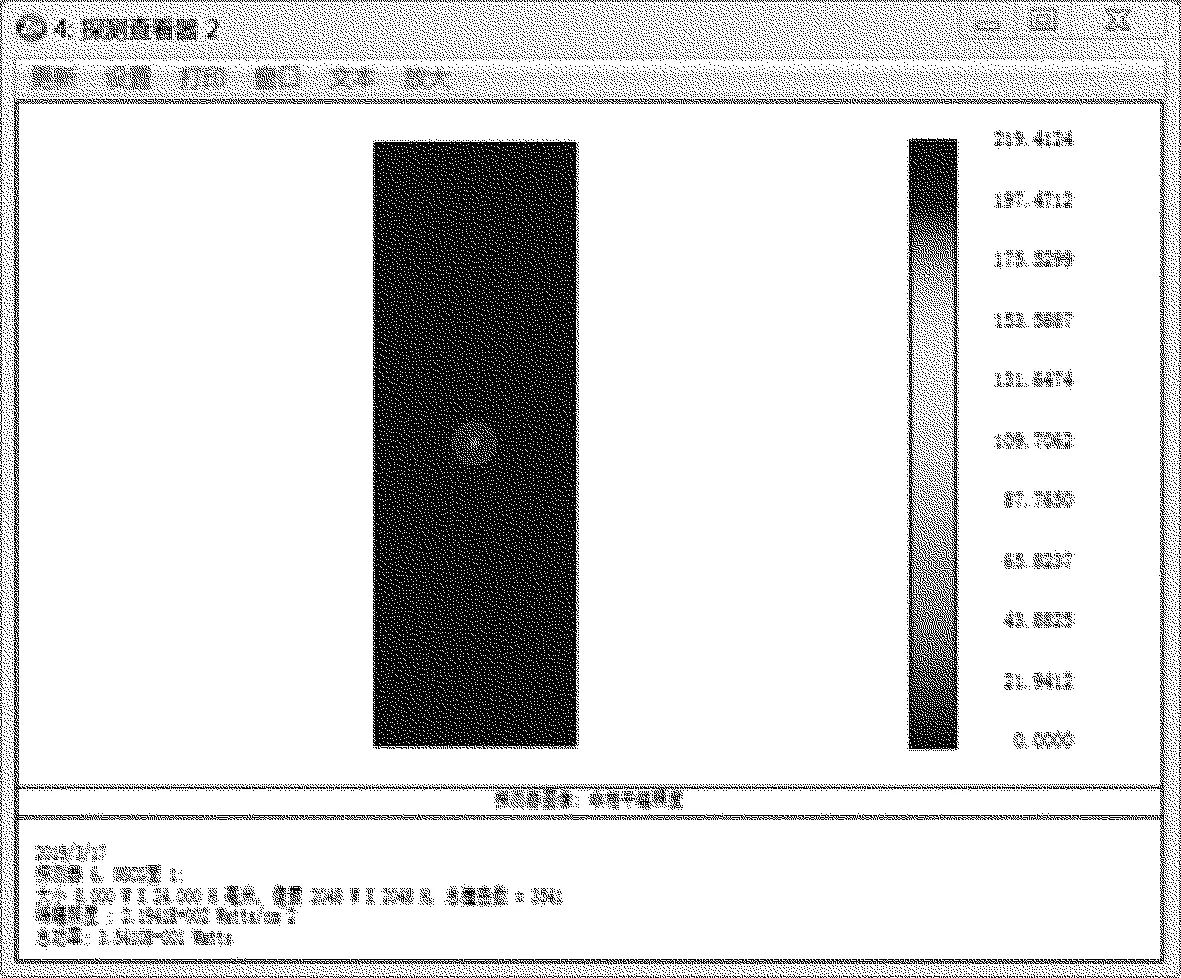
Fig.9 View of double convex lens detector

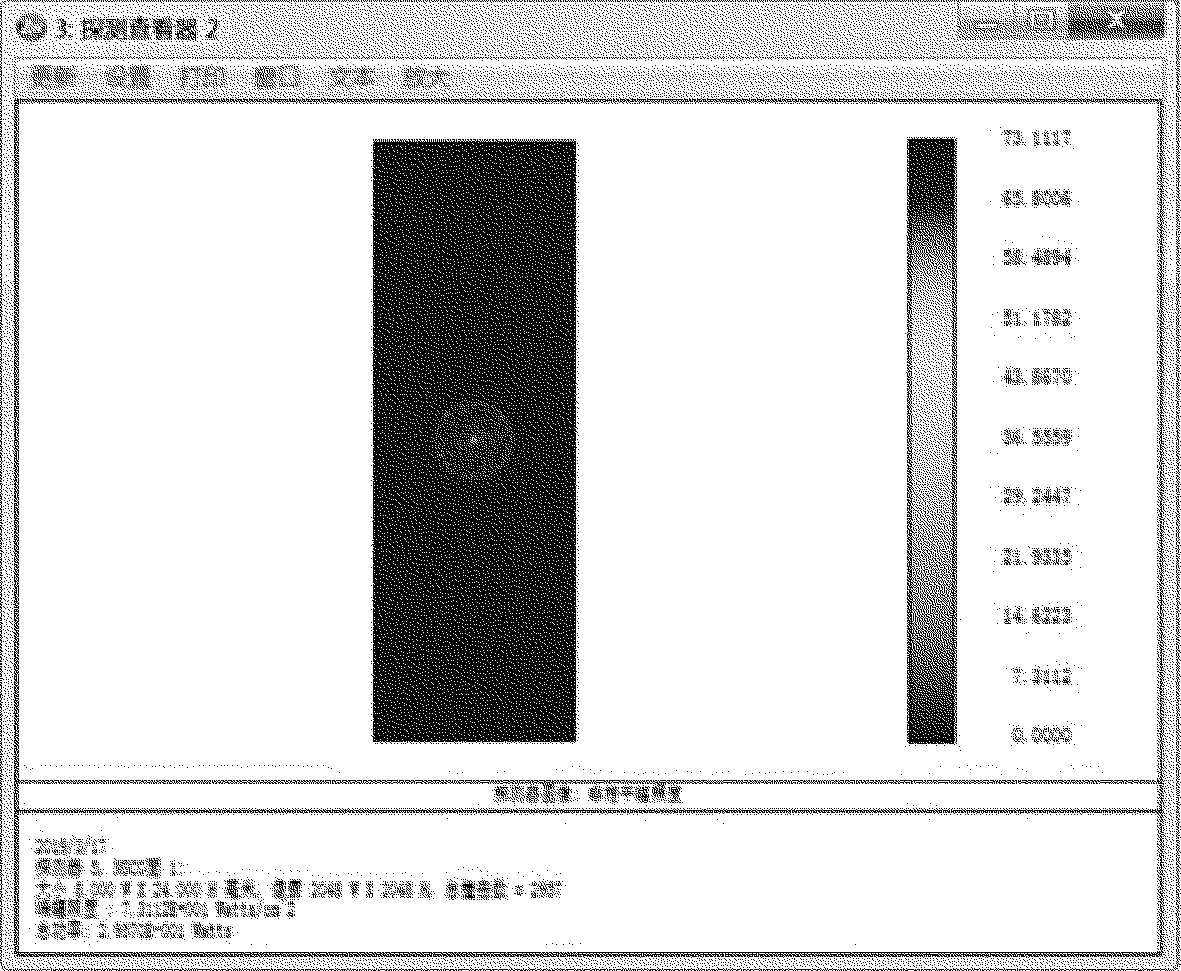
Fig.10 View of symmetrical plano-convex lens detector

Table 1 Comparison diagram of probe view data

(3)進行點列圖仿真分析。在理想狀態下，由一個點光源發出的所有光線在通過一個比較理想的光學系統之后，會匯聚到一個點，這就是這個物點的像點。[11]但是在實際光學系統的應用過程中，因為不可能不存在像差，所以經過光學系統用探測器查看后會形成一個光斑，稱其為彌散斑。探測器上的視圖稱為點列圖。

點列圖實際代表的是光斑分布的密集狀況，越密集說明成像質量越好。衡量點列圖光斑分布情況可以用幾何最大半徑值(geometric maximum radius,GEO)和均方根(root mean square,RMS)半徑值來進行表示[12]。幾何最大半徑值就是以參考光線點為中心，包含所有光線的最大圓的半徑，而均方根半徑則是每條光線交點與參考光線點的距離的平方，除以光線條數后再開方[13]。也就是說均方根半徑值反映了光能的集中程度，幾何最大半徑反映了像差的最大值。這兩個的值越小，說明成像質量越好[14]。

圖11和圖12是兩種系統光學仿真后得到的點列圖。由圖11可知,對稱式平凸透鏡點列圖的GEO為1182.71μm，RMS為671.872μm。圖12中雙凸透鏡點列圖的GEO為6798.75μm，RMS為2501.57μm。比較兩種系統數據，對稱式平凸透鏡的幾何最大半徑值和均方根半徑值遠小于雙凸透鏡點列圖的值，兩個系統的幾何最大半徑之比為：1182.71μm/6798.75μm=17%。所以對稱式平凸透鏡的彌散斑直徑更小，成像質量更佳[15]。

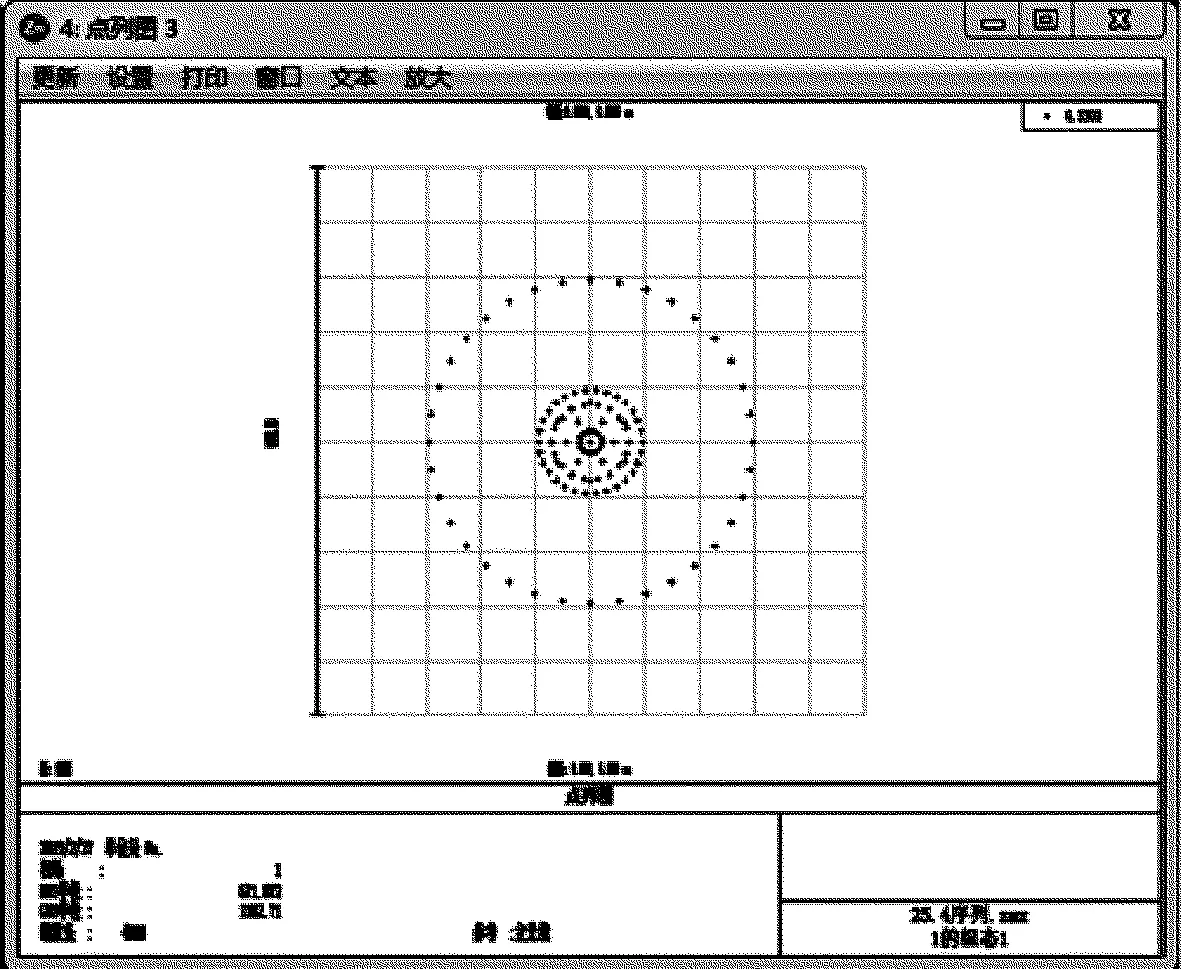
Fig.11 Point series diagram of double convex lens detector

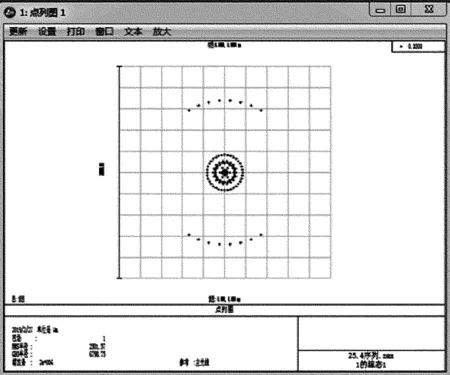
Fig.12 Point series diagram of symmetrical plano-convex lens detector

經過上述對比不難發現,從NSC陰影模型圖中光線的匯聚、探測器探測視圖以及點列圖中彌散斑半徑大小均可得到對稱式平凸透鏡的成像質量要優于一個雙凸透鏡的結果。

3 結 論

運用光學仿真軟件ZEMAX，在目前監測儀器的熒光采集光路基礎上對其進行了優化設計。對比探測視圖和點列圖后發現優化后的峰輻強度是之前的3倍，總功率達到了0.35410W，有效半徑和均方根半徑都大幅度減小，達到了優化的目的。在與光源距離相同的條件下，對稱式平凸透鏡相較于雙凸透鏡不僅結構簡單、安裝方便、光能損失較小而且成像質量相對較好。因此，對稱式平凸透鏡結構能夠很好地應用于熒光的檢測。