等高線模式下的一類幾何最值問題的再探究①

鄧 清 夏小剛

(1.貴陽(yáng)市烏當(dāng)中學(xué) 550018;2.貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院 550025)

數(shù)學(xué)是模式的科學(xué)，數(shù)學(xué)的本質(zhì)特征就是在模式化的個(gè)體抽象中對(duì)模式進(jìn)行研究.[1]波利亞認(rèn)為，在解決一個(gè)自己感興趣的問題后，要善于去總結(jié)一個(gè)模式，并把他儲(chǔ)存起來，以后才可以隨時(shí)用它去解決類似的問題，進(jìn)而提高自己的解題能力.波利亞在他的著作中概括了幾個(gè)數(shù)學(xué)模式，其中，“相切的等高線模式”是探究極值點(diǎn)的一種方法.筆者閱讀思考后發(fā)現(xiàn)，運(yùn)用該方法探究幾何中的一類最值問題時(shí)，會(huì)有一種全新的體驗(yàn)，特與大家分享.

1 “相切的等高線模式”解讀

如果問題中能找到一系列等高線，穿過給定路徑(或與給定路徑有多于一個(gè)交點(diǎn))的等高線上不可能達(dá)到極值點(diǎn)，只有與給定路徑相切的等高線，其切點(diǎn)處才有可能達(dá)到極值點(diǎn).[2]這就是“相切的等高線模式”.該模式中，“等高線”原本指的是地形圖上高程相等的相鄰各點(diǎn)所連成的閉合曲線，在這里指的是使得問題中所求變量f的值相等的所有點(diǎn)組成的曲線，因此也可以稱作“等值線”.為了弄清楚該模式的意義，我們先來看這樣一個(gè)例子：

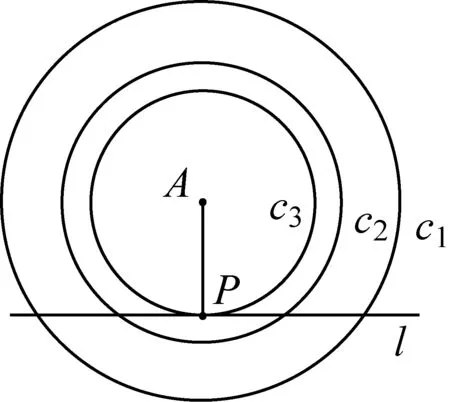
圖1

如圖1，在已知直線l上求一點(diǎn)P，使得它與已知點(diǎn)A有最小距離.問題中要求的變量f是到點(diǎn)A距離問題，那么等高線就是到點(diǎn)A距離相等的點(diǎn)的集合，也就是以A為圓心的一組同心圓.點(diǎn)P既要在等高線上，又要在給定路徑——直線l上，根據(jù)“相切的等高線模式”的概念，當(dāng)且僅當(dāng)?shù)雀呔€與直線……