單軸旋轉慣導緯度誤差和航向誤差關聯性分析

王 超，郭正東，高大遠，朱海榮

（海軍潛艇學院，山東青島266199）

慣導航向信息是艦船導彈發射的重要基準信息，慣導航向精度直接決定了艦船導彈武器系統的作戰效能。目前，單軸旋轉激光陀螺慣導系統已廣泛應用于國外水面作戰艦船，以保障艦船自主導航和為艦船武器系統發射提供信息基準[1-4]。此外，慣導姿態精度也直接影響航天測量船測控設備的外測精度[5]。在海上動態條件下，受海況、艦船運動等因素的影響，艦船姿態不斷變化。海上長時間工作的艦船慣導系統，受各種誤差因素的影響，其航向精度不斷變化，一般可通過天文導航或GPS姿態測量方式，獲取高精度航向參考信息，實現對艦船慣導航向誤差進行測量和補償[6-8]。而對于長時間海上航行的艦船而言，當受到氣候或其他因素影響，無法適時進行星體測量時，即便能夠獲取準確的位置參考信息，也無法對艦船慣導航向誤差進行實時動態評估。

考慮單軸旋轉慣導緯度誤差和航向誤差都是在相同誤差源的作用下，由慣性導航解算輸出的結果，通過研究引起單軸旋轉慣導航向誤差和緯度誤差的機理，并進行比較分析，確定二者之間的關聯性，在無外界參考航向信息情況下，為實現海上艦船單軸旋轉激光陀螺慣導航向誤差實時動態評估與補償，提供一種新的思路和方法。

1 引起單軸旋轉慣導緯度誤差機理分析

單軸旋轉慣導系統誤差因素主要包括初始誤差、陀螺漂移、加速度計偏差、安裝誤差、標度因數誤差和隨機誤差等。

單軸旋轉可以自動補償與轉軸垂直方向的加速度計零位偏差、陀螺常值漂移、安裝誤差和對稱性標度因數誤差等。等效方位陀螺常值漂移和初始姿態誤差是影響單軸旋轉慣導系統導航誤差最主要的因素[9-13]。

根據旋轉慣導系統誤差方程[14]，主要考慮等效方位陀螺常值漂移和初始姿態誤差的影響，解算出靜基條件下的單軸旋轉慣導緯度誤差的表達式為：

式（1）中，a1、a2、a3、a4分別為誤差系數，各誤差系數表達式為：

式（2）中：δφ(t)為慣導緯度誤差；εU為慣導等效方位陀螺常值漂移；φE0、φN0、φU0分別為慣導姿態角初始誤差；φ 為艦船緯度；ωie為地球自轉角頻率；ωs為舒拉周期振蕩角頻率。

根據式（1）和式（2），緯度誤差在等效方位陀螺漂移的作用下，引起緯度舒拉周期振蕩誤差、地球周期振蕩誤差和誤差分量kεU等。

在動基座條件下，艦船緯度不斷變化，在一段時間內，當緯度變化不大時，誤差分量kεU可近似為緯度常值誤差分量，可通過計算該時間段內的緯度誤差均值獲得。如當緯度為36°時，等效方位陀螺常值漂移為0.001(°)/h 時，引起的誤差分量kεU約為0.184 9′，當緯度為76°時，引起的誤差分量kεU約為0.055 3′；在初始姿態誤差的影響下，主要引起緯度舒拉周期振蕩誤差和地球周期振蕩誤差。通過將慣導系統工作在水平阻尼狀態[15-16]，可消除慣導誤差中受傅科周期調制的舒拉周期振蕩誤差分量，在水平阻尼工作狀態，式（1）中的系數表達式為：

利用式（4）對式（3）進一步化簡，得：

根據式（5），在水平阻尼工作狀態下，當載體緯度變化較小時，在等效方位陀螺漂移的作用下，引起單軸旋轉慣導緯度地球周期振蕩誤差和近似緯度常值誤差分量；在初始姿態誤差等誤差源的作用下，主要引起緯度地球周期振蕩誤差。

2 引起單軸旋轉慣導航向誤差機理分析

根據單軸旋轉慣導系統誤差方程，主要考慮等效方位陀螺常值漂移和初始姿態誤差的影響，解算出靜基條件下的單軸旋轉慣導航向誤差的表達式為：

式（6）中，b1、b2、b3、b4分別為上式中的誤差系數。

由于在水平阻尼工作狀態下，受傅科周期振蕩調制的舒拉周期振蕩誤差分量受到抑制，慣導航向誤差主要呈現地球周期振蕩特點，則在水平阻尼工作狀態下，式（6）中的系數表達式為：

利用式（4）對式（7）進一步化簡，得：

根據式（8），各誤差源對應系數均呈現地球周期振蕩，即在等效方位陀螺常值漂移和初始姿態誤差等誤差源的作用下，慣導航向誤差呈現地球周期振蕩特點。

3 單軸旋轉慣導緯度誤差和航向誤差關聯性分析

對比式（5）和式（8），則由等效方位陀螺漂移引起的緯度誤差和航向誤差系數表達式為：

由初始姿態誤差引起的緯度誤差和航向誤差系數表達式為：

根據式（9）（10）可知，當補償緯度誤差分量kεU后，在水平阻尼狀態下，等效方位陀螺常值漂移和各初始姿態誤差分別引起慣導緯度和慣導航向地球周期振蕩誤差。引起的地球周期振蕩誤差的幅值和相位關系如表1所示。

表1 單軸旋轉慣導緯度誤差和航向誤差比較Tab.1 Comparison of latitude error and heading error of SRSINS

表1中：AbiAai為式（9）和式（10）中不同誤差源對應單軸旋轉慣導緯度誤差和航向誤差系數地球周期振蕩幅值比，i=1,2,3；θbi-θai為式（9）和式（10）中不同誤差源對應緯度誤差和航向誤差系數地球周期振蕩相位差，i=1,2,3。根據表1可知，在等效方位陀螺常值漂移和初始姿態誤差等誤差源的作用下，單軸旋轉慣導航向誤差地球周期振蕩幅值為緯度誤差地球周期振蕩幅值的sec φ 倍，航向誤差地球周期振蕩相位比緯度誤差地球周期振蕩相位提前π2。因此，在等效方位陀螺常值漂移和各初始姿態誤差作用下，當補償緯度誤差分量kεU后，水平阻尼狀態下單軸旋轉慣導緯度誤差和航向誤差關聯性模型如下：

式（11）中：Aδφ為緯度誤差中地球周期振蕩誤差分量的幅值；AφU為航向誤差中地球周期振蕩誤差分量的幅值；θδφ為緯度誤差中地球周期振蕩誤差分量的相位；θφU為航向誤差中地球周期振蕩誤差分量的相位。

根據式（11），航向誤差中地球周期振蕩誤差分量的幅值是緯度誤差中地球周期振蕩誤差分量幅值的sec φ 倍，緯度誤差中地球周期振蕩誤差分量的相位與航向誤差中地球周期振蕩誤差分量的相位相比，延遲π2。

以上主要考慮等效方位陀螺常值漂移和初始姿態角誤差等主要誤差源的影響。實際上，影響慣導航向誤差和緯度誤差的誤差源還包括隨機誤差、安裝誤差、標度因數誤差等。由于這些誤差源影響相對較小，式（11）同樣適用于單軸旋轉慣導多種誤差源共同作用下緯度誤差和航向誤差之間的關聯性。在水平阻尼工作狀態下，確定單軸旋轉慣導緯度誤差和航向誤差存在如下關聯性：①緯度誤差主要包括地球周期振蕩誤差和誤差分量kεU，航向誤差主要為地球周期振蕩誤差；②航向誤差地球周期振蕩幅值為緯度誤差地球周期振蕩幅值的sec φ 倍；③航向誤差地球周期振蕩相位比緯度誤差地球周期振蕩相位提前π2。通過以上分析，利用水平阻尼狀態下的單軸旋轉慣導緯度誤差和航向誤差的關聯性，為實現慣導航向誤差實時動態評估提供一種新的思路和方法。

4 仿真實驗驗證

1）仿真實驗設計。為驗證利用緯度誤差與航向誤差關聯性，在仿真實驗設計中，結合當前文獻中高精度旋轉激光慣導中激光陀螺和加速度計的主要技術參數以及安裝誤差、標度因數誤差、初始誤差等誤差參數[17-18]，設置仿真實驗條件。根據單軸旋轉激光陀螺慣導運動學方程，建立水平阻尼單軸旋轉激光慣導仿真模型，將慣性導航解算輸出的導航參數與參考基準進行比較，獲得水平阻尼工作狀態下的單軸旋轉激光陀螺慣導緯度誤差和航向誤差仿真數據，單軸旋轉慣導誤差仿真過程見圖1。以仿真輸出的緯度誤差和航向誤差數據為對象，利用仿真輸出的緯度誤差，通過計算和補償緯度誤差常值分量，根據式（11）對航向誤差進行實時動態估計，比較實時動態估計的航向誤差與仿真輸出的實際航向誤差之間的變化特點，驗證單軸旋轉慣導緯度誤差與航向誤差關聯性分析的正確性。

圖1 單軸旋轉慣導誤差仿真示意圖Fig.1 Simulation diagram of error of SRSINS

結合文獻中激光慣導中激光陀螺和加速度計的主要技術參數以及安裝誤差、標度因數誤差、初始誤差、單軸旋轉方案等參數[1，12]，設置仿真條件如下：3個激光陀螺的常值漂移均為0.001(°)/h，隨機漂移標準差均為0.000 5(°)/h；3 個加速度計的零偏均為0.01 mg，隨機白噪聲標準差為0.005 mg；陀螺和加速度計的對稱性標度因數誤差均為2 ppm ；安裝誤差陣為[0,4″,-4″;-4″,0,4″;4″,-4″,0] ；初 始 姿 態 誤 差 為[1 .0′,1.0′,2.0′] ；初始航向為90°，初始經度、緯度分別為122 °E 和76° N，慣導一直工作在水平阻尼狀態，仿真時間為30 d。

2）仿真結果與分析。在水平阻尼狀態下，單軸旋轉慣導緯度誤差和航向誤差如圖2所示。

圖2 緯度誤差與航向誤差仿真曲線Fig.2 Simulation curve of latitude error and heading error

實線表示單軸旋轉慣導仿真輸出的緯度誤差;虛線表示單軸旋轉慣導仿真輸出的航向誤差。由圖2可知，在水平阻尼工作狀態下，慣導緯度誤差和航向誤差均主要呈現地球周期振蕩性特點，且地球周期振蕩幅值隨時間發生變化。如在0～10 d時間段內，緯度誤差 變 化 范 圍 為( - 1.6′,1.8′) ；航 向 誤 差 變 化 范 圍 為( - 6.7′,7.1′) ，在11～20 d 時間段內，緯度誤差變化范圍為(- 1.7′,1.8′) ，航向誤差變化范圍為( - 7.5′,7.2′) ；在21～30 d 時間段內，緯度誤差變化范圍為(- 1.6′,1.7′) ，航向誤差變化范圍為( - 7.3′,7.0′) 。在不同時間段內，慣導緯度誤差和航向誤差的標準差和誤差均值如表2所示。

表2 不同時間段內的緯度誤差和航向誤差Tab.2 Latitude error and heading errorin different periods

由表2可知，在不同時間段內，單軸旋轉慣導航向誤差標準差與緯度誤差*sec φ 基本保持一致，慣導航向誤差的標準差值約為緯度誤差標準差值的sec φ倍；緯度誤差均值主要與等效方位陀螺常值漂移引起的誤差分量有關。結合仿真條件參數，在相應時間段內，艦船緯度為76 °N，表2 中緯度誤差均值與誤差分量kεU計算值相近，與前面單軸旋轉慣導緯度誤差和航向誤差關聯性分析結果一致。

為進一步驗證單軸旋轉慣導緯度誤差和航向誤差地球周期振蕩相位之間的關系，根據單軸旋轉慣導緯度誤差和航向誤差關聯性模型，在補償緯度誤差均值的基礎上，對緯度誤差地球周期振蕩幅值和相位進行相應調整，可獲得慣導航向誤差實時動態估計值。取圖2 中10～25 d 時間段內的緯度誤差和航向誤差數據，在計算并補償緯度誤差常值分量的基礎上，根據式（11），利用慣導緯度誤差對慣導航向誤差進行動態估計，如圖3所示。

圖3 中，點虛線為利用慣導緯度誤差估計出的航向誤差曲線，實線為單軸旋轉慣導仿真輸出的實際航向誤差曲線。從圖中可以看出，估計的航向誤差曲線與實際航向誤差曲線在振蕩周期、振幅和相位等方面都較好地保持了一致性，從而驗證了單軸旋轉慣導緯度誤差和航向誤差之間關聯性分析的正確性。同時，驗證了利用慣導緯度誤差實現對航向誤差進行實時動態估計可行性。利用估計的慣導航向誤差對慣導實際航向誤差進行補償，如圖4所示。

圖3 單軸旋轉慣導航向誤差曲線Fig.3 Curve of heading error of SRSINS

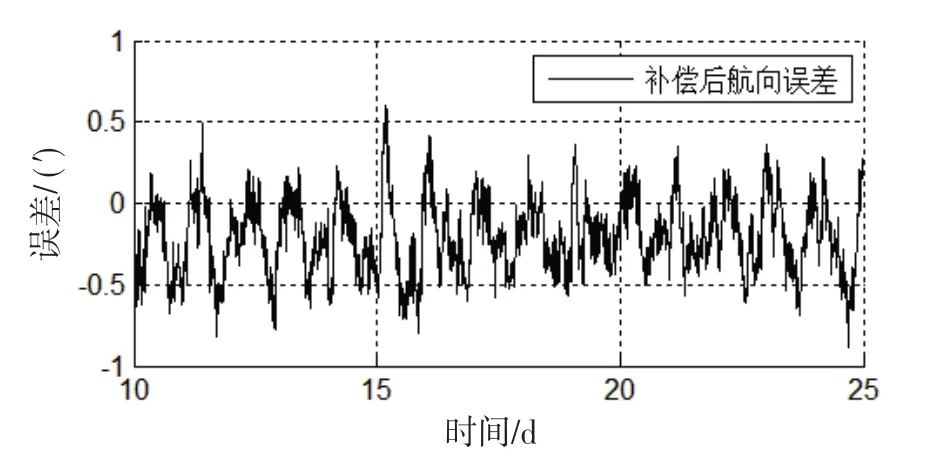
圖4 補償后航向誤差曲線Fig.4 Curve of heading error after compensation

根據圖4，利用估計的慣導航向誤差對慣導航向誤差補償后，慣導航向誤差明顯降低，振蕩范圍約為( - 0.89′,0.61′) ，標準差約為0.23′，與補償前單軸旋轉慣導實際航向誤差相比，航向誤差振蕩范圍減小了89.8%，航向誤差標準差減小1個數量級以上，大大提升了單軸旋轉慣導航向精度。

5 結論

為分析在相同誤差源作用下的單軸旋轉慣導緯度誤差和航向誤差間的關聯性，通過研究引起單軸旋轉慣導航向誤差和緯度誤差的機理，并進行比較分析，建立了單軸旋轉慣導緯度誤差與航向誤差間的關聯性模型，為實現無外界參考航向信息情況下的艦船單軸旋轉慣導航向誤差動態評估與補償，提供了一種新思路，對提高艦船慣導航向精度，保障艦船航行安全和提升艦船武器系統作戰效能具有重要實用價值。