土星環形成機理探究

張重陽

（上海市張堰中學，上海 201514）

1.緒論

1.1 研究背景及意義

太陽系中有八大行星，按距離太陽由近到遠的順序分別是：水星、金星、地球、火星、木星、土星、天王星、海王星，但其中只有土星和天王星具有圍繞其自身中心天體旋轉的環狀結構。隨著對土星環幾百年來的不斷觀測研究，人類已經對土星環有了較為全面的認識：土星環寬度從30km ～30 萬km 不等，距離土星從近到遠按被發現的順序分別命名為D、C、B、A、F、G 和E 環。其中，B 環最寬、最亮，總質量也最大。A、B、C 三個較為明亮密集的環被稱為主環。其他環相比之下則暗淡并且分散得多，基本都是被飛掠土星的人造探測器所發現。對比太陽系內的其他行星，僅土星與天王星具有類似的環狀結構，故而推測土星環的形成并非偶然，其背后必定蘊含著豐富的物理學原理。本文將通過物理建模，對土星環的形成機理進行了初步探究，通過理論計算驗證了土星具備形成環狀結構的必要條件，從而為土星環的形成提供了科學支撐。

1.2 國內外研究現狀

對天體力學理論及其觀測研究已有很多相關研究工作，周濟林、孫義燧通過計算行星引力勢[1]，并考慮土星環內部小天體之間的碰撞對土星環動力學進行了研究，并歸納了行星環的分析方法。陳健,夏芳等對雙星觀測計算方法進行了改進[2]，以牛頓二體模型作為理論基礎，通過立體幾何改進了雙星的觀測方法，從而解決了傳統方法對透鏡效應的忽略，文章將理論結果與實際觀測數據進行了擬合對比，結果表明所提出的方法極大地改良了原有模型，具有一定的使用價值。劉林，湯靖師等對地球與月球系統平動點軌道的特征問題進行了研究[3]，對軌道由于不穩定特性引起的誤差傳播問題進行了詳細的理論研究，并給出了高精度軌道預報方法，并利用實際測量資料對定軌結果進行了檢驗。夏睿奇對地球特洛伊天體穩定性進行了研究[4]，指出共振對地球特洛伊天體的穩定區域的分布情況存在重要作用。何加川對天體力學的發展歷史以及近代以來的關鍵性成果進行了綜述[5]，并將天體力學的研究范疇劃分為：自轉理論、天體形狀、多體問題、天文動力學、數值方法以及攝動理論6 個方向，在對天體力學的成果進行歸納總結的基礎上提出了相應的展望，為未來研究指明方向。

本文對土星環的形成機理進行了研究，經過簡單的建模并通過引力計算，得出了兩個重要的崩解臨界，并進一步指出土星環可能由大質量的天體落入崩解半徑后分解成小碎塊兒，從而繞土星旋轉形成土星環。

2.土星環運動方程

2.1 土星與土星環的基本概況

土星主要是由氫氣構成的氣態行星，其赤道半徑達到6 萬多km，在太陽系行星中并非質量最大的一顆，其質量僅在太陽系行星中位列第二。但除了常見的衛星以外，土星還具有奇特的環狀結構稱為土星環。據天文觀測數據，土星環主要由水、冰、石塊兒等小顆粒組成。有研究表明與形成于45 億年前的土星相比，土星環的形成歷史相對短暫，它形成于約1000 萬年～1 億年前。在天文望遠鏡下，土星環分布在土星周圍具有非常明亮的光澤，環中有不計其數的小顆粒，其大小橫跨微米級到米級，在土星引力的作用下圍繞土星運轉。

2.2 土星與土星環的相互作用力

土星環作為有質量的物體，在土星周圍將受到土星的引力作用，其大小與土星和土星環質量的乘積成正比，而與它們之間距離的平方成反比。

其中，G 為萬有引力常數，由卡文迪許使用扭秤裝置測出，其值約為6.67×10-11N·m2/kg2。M 和m 分別表示土星與土星環的質量，r 表示土星與組成土星環的天體間的距離，則F 即為土星與土星環之間相互作用的引力。

考慮到土星環與太陽和其他天體的距離很遠，而引力與距離呈平方反比衰減，故而在研究過程中可忽略其他天體對土星環引力作用，而僅考慮土星與土星環之間的相互作用力。

2.3 土星環運動的軌道參數

土星環以土星為中心天體，在土星引力的作用下圍繞土星運動。由開普勒行星運動定律可知，土星環繞土星運動的軌跡為橢圓，且土星位于橢圓的焦點。但考慮到土星環繞土星運動的偏心率很小，可將土星環軌道簡化為正圓軌道。根據圓周運動的基本規律，由萬有引力提供向心力得：

其中：M 和m 分別表示土星與土星環的質量；r 表示土星環與土星之間的距離，ω 為土星環繞土星運動的角速度，v 為土星環繞土星運動的線速度，T 為土星環的運動周期。

由式(2)可得：

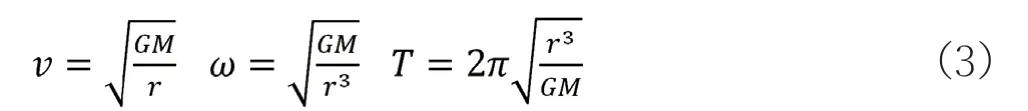
可見土星環的運動情況與其距土星的距離相關，離土星距離越近的環其運動的線速度、角速度越大，周期越短。

由式(3)可知，土星環內側與外側運動角速度之差：

其中：M 表示土星的質量；r1與r2分別表示土星環內側與外側與土星之間的距離，Δω 為土星環內側與外側的角速度差，d 為土星環寬度。

可見，土星環寬度越大，土星環內側與外側的角速度差越大。若土星環為一個整體圓盤，則其內外側角速度應當相同，但根據實際觀測可知，土星環內側與外側繞土星運動的角速度具有明顯差異，從而說明土星環并非是一個整體圓盤模型，而是由眾多小質點構成的相互離散的系統。

3.土星環形成機理建模

3.1 土星環起源假說

在太陽8 大行星中，僅土星和天王星存在環狀結構，可見類似的環狀結構在太陽系天體中不是普遍現象，其形成應當具備一定的條件。土星在太陽系中質量與體積均位列木星之后，但木星以及其他行星卻未形成環狀結構，故而猜測土星的環狀結構來源有：

（1）土星眾多的衛星中，曾經有一顆含水量豐富的小衛星。它在運行過程中受到內側的土星和外側其它衛星的多方向引力作用，最終崩解碎裂。

（2）土星系統中衛星眾多，引力環境復雜，這使土星的衛星們始終處于不規則的引力拉扯中。它們的內部不斷因形變摩擦而升溫，最終形成劇烈的間歇泉噴發（噴發物以水為主）形成了土星環。

3.2 土星環形成的機理建模

為簡化問題分析，本文對土星環形成的崩解假說建立了兩類理論模型，所建立的模型從外來天體的構成區分，分別為由引力結合的雙體模型以及由質點群結合的單體模型。并研究了在土星引力的作用下，外來天體模型受到土星引力而崩解的情況，進而推導出各自的崩解臨界。

3.2.1 由引力結合的雙體模型

由引力結合的雙體模型考慮外來天體是由兩個質量均為m 半徑為r 的規則球體組成，其自身僅依靠彼此的引力相互結合。如圖1 所示。

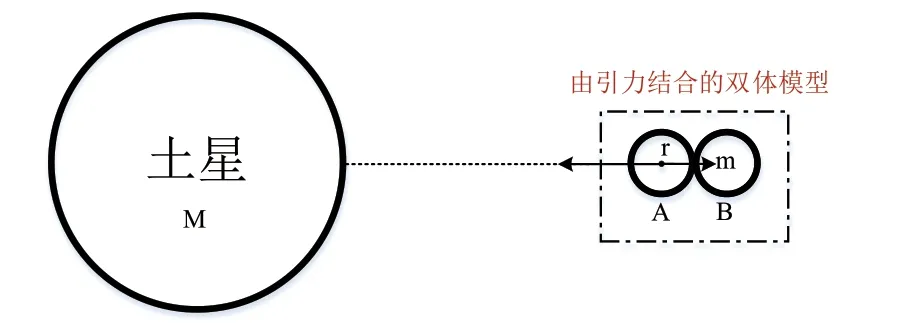
圖1 由引力結合的雙體模型示意圖

由圖1 可知，對于由引力結合的雙體模型中的任一天體A、B 而言，其均受到兩個引力的作用，即土星的引力以及自身另一天體的結合引力。其中，土星引力的作用是將雙體模型分離，而A 與B 自身的引力將其牢牢結合。隨著雙體模型逐漸靠近土星，土星對雙體模型中天體A 的引力逐漸增強，而A 與B 的結合引力由于它們的距離不變，該結合引力為常數：

其中，FAB即為A 與B 的結合引力，G 為萬有引力常數，m，r 分別為雙體模型內部兩個天體的質量與半徑。

隨著雙體模型逐漸靠近土星，土星對雙體模型的引力逐漸增大，式(6)當土星對雙體模型中天體A 的引力大于A 與B 的結合引力時，雙體模型將會發生崩解，從而使得雙體模型的每一部分成為繞土星運動的土星環。

其中，F土表示土星對天體A 的引力，G 為萬有引力常數，M 和m 分別表示土星的質量與雙體模型中天體A的質量，R 與r 分別為土星到天體A、B 切點之間的距離以及天體A 的半徑。當F土大于FAB時，雙體模型中天體A、B 發生崩解，聯立式(5)與式(6)可知：

求解上式可得：

其中：M 和m 分別表示土星的質量與雙體模型中天體A 的質量，R 與r 分別為土星到天體A、B 切點之間的距離以及天體A 的半徑。

當雙體模型離土星足夠近時，由于土星對天體A 的引力大于雙體模型AB 之間的結合引力，故而導致天體A 受到土星引力而與天體B 分離，即雙體模型崩解形成土星環的一部分。

由式(8)可以看出，雙體模型崩解極限半徑R 與雙體模型內天體A、B 的半徑成正比，體積越大的天體越容易受天體引力作用而發生崩解。同樣的，雙體模型崩解極限半徑R 與雙體模型內天體A、B 的質量成負相關，雙體模型內天體的質量越大，其結合引力越強，越不容易受到行星引力作用發生崩解。另外，崩解極限半徑還與行星質量相關，行星質量越大，其對雙體模型內天體的“撕扯”作用越強，越容易使雙體模型發生崩解。

若雙體模型內天體密度均勻，考慮到雙體模型內天體A、B 半徑遠小于行星半徑，則式(8)可進一步近似為：

可見，雙體模型的崩解半徑與其平均密度及尺寸呈負相關，而與行星質量呈正相關。質量越大的行星越具備形成行星環的可能。

3.2.2 由質點群結合的單體模型

雙體模型較為簡單，便于進行理論分析，但雙體模型與實際天體的崩解方式可能存在差異。為此，本文建立了由質點群結合的單體模型，用來模擬外來天體受行星引力發生崩解的物理過程，如圖2 所示。

圖2 由質點群結合的單體模型示意圖

在質點群模型中，各質點分別受到來自土星的引力以及自身其他質點產生的結合引力。當質點群離行星較遠時，其自身結合引力大于行星引力，從而使質點群保持穩定結合。然而，隨著質點群模型逐漸靠近土星，土星對模型內各質點的引力逐漸增大，當土星對質點群內質點的引力大于其自身的結合引力時，質點群模型將會發生崩解，成為繞土星運動的土星環。

在質點群模型內部眾多質點中，P 點離行星最近受行星引力影響最大，因而也發生崩解，計算P 點的加速度：

其中，ap為P 點加速度，G 為萬有引力常數，m，r分別為質點群構成的球體總質量與半徑，R 為土星到質點群質心的距離。

可見，質點P 的加速度決定于質點群質心到行星的距離。在行星引力的作用下，質點群質心的加速度為：

隨著質點群模型逐漸靠近土星，ap逐漸增大，當ap＞ao時，質點P 脫離質點群模型內其他質點的引力束縛發生崩解，即：

化解可得：

考慮到R 遠大于r，上式可進一步寫成：

可見，對于質點群模型而言，其崩解極限半徑與質點群所組成的球體尺寸成正比，而與質點群總質量成反比，這是因為質點群尺寸越大結合就越松散，土星引力更容易將其“撕碎”。式(14)所得崩解半徑與行星質量呈正相關，這與雙體模型得出的結論是一致的，即質量越大的行星越容易形成行星環。

3.3 模型的局限性

本文3.2 節通過引力理論對土星環的成因進行了分析，建立了由引力結合的雙體模型以及由質點群結合的單體模型兩個簡易機理模型，并推導了相應模型的崩解極限。本文假設條件較為理想，模型在幾何形狀上為規則的球體，且模型內在的結合力為天體自身的引力。實際上的外來天體形狀多樣，諸如啞鈴型、橢球形等，其內在的結合力也不單純為引力，還存在物質之間的化學鍵作用，從而使其結合力更強，實際的崩解半徑比本文理論模型計算所得更小。

4.結論

土星作為太陽系最獨特的行星之一，其周圍具有一圈繞行星本體運動的行星環。本文利用萬有引力理論對土星環的形成機理進行了初步探究，通過研究土星環圍繞土星的運動情況，提出土星環可能由大質量外來天體在土星引力作用下崩解而形成，進而建立了相應的崩解模型，推導了兩個理論崩解極限半徑。理論計算結果表明，平均密度越小、體積越大的外來天體更易發生崩解，而中心天體質量越大則其形成行星環的概率也就越大，通過建立簡易物理模型對土星環形成的機理從理論上作出了科學解釋。