尾部特征參數對氣動阻力交互影響與全局優化研究

張勇　石佳琦　谷正氣　劉水長　米承繼

摘? ?要：汽車尾部結構氣動減阻優化時，各幾何特征參數間往往存在此消彼長的現象，使得優化變得盲目而復雜. 對此，為探明關鍵幾何參數的交互影響規律，以Ahmed類車體為研究對象，在HD-2風洞試驗對標驗證基礎上，對后背3個主要特征參數進行了CFD仿真研究，并在此基礎上，為克服盲目性，應用集成優化平臺對尾部特征參數進行優化設計. 結果表明，后背傾角角度對減阻的貢獻量最大，背部兩側圓角半徑次之，后背頂部圓角半徑最小;三者的改變對氣動阻力的影響都具有非單調性;當后背傾角角度、后背頂部圓角半徑和背部兩側圓角半徑分別為13°、283 mm、58 mm時，能有效減小氣動阻力，減阻率達到11.76%，為具體車型減阻優化研究提供借鑒.

關鍵詞：尾部特征;交互影響;Ahmed模型;減阻

中圖分類號：U461.1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Abstract：In the aerodynamic drag reduction optimization of automobile tail structure，there is a phenomenon between geometrical characteristic parameters，which makes optimization become blind and complex. In order to ascertain the interaction law of the key geometrical parameters，this paper carried the CFD simulation research of the three main characteristic parameters on the back of the Ahmed model on the basis of the HD-2 wind tunnel experiment. In order to overcome the blindness of optimization，the integrated optimization platform was applied to optimize the tail characteristic parameters. The results show that the angle of the back inclination has the greatest contribution to drag reduction，the two sides rounded corners on the back has the smaller contribution，the contribution of the top corner of the back is the smallest. The influence of the change of three variables on the aerodynamic resistance is non-monotonic. When the values of the angle of the back inclination，the top corner of the back and the two sides rounded corners on the back are 13°，283 mm and 58 mm respectively，the drag reduction rate reaches 11.76%. This paper provides a reference for the study of the optimization of drag reduction in specific models.

Key words：tail characteristic;interaction effect;Ahmed model;drag reduction

通過汽車車身三維曲面造型優化，降低氣動阻力以提高燃油經濟性，是汽車車身設計師的慣用方法. 然而汽車車身是由三維復雜曲面組成的片體結構，尤其是作為湍動能的主要耗散區的汽車尾部，包含了諸多曲面，每個曲面又包含諸多特征參數，改變造型特征某一參數，均會引起周圍流場結構的改變，進而對氣動特性產生不同影響，即存在著不同幾何特征參數氣動減阻優化的此消彼長的交互影響，而這種影響具有不確定性，即優化變量的盲目和未知性[1-2]，這使得車身減阻成為復雜的優化問題. 目前常用的做法只能依賴于工程師經驗，開展大量重復性仿真計算基礎上的部分特征參數的優化，不能保證該部位的全局最優.

對此，在不改變汽車車身造型固有風格條件下，對經典的汽車模型尾部特征參數交互影響機理進行分析，開展全局優化研究，以指導具體車型開發，就顯得尤為必要.

Ahmed車型作為經典的斜背車體，常用于汽車空氣動力學對標研究[3-6]. Thacker等[7]對其車頂與后背連接處圓角優化，減阻達到10%;Grandemange等[8]對后背傾角角度進行結構優化，使得尾部產生了4個縱向漩渦，實現整體減阻5.8%;Evrard等[9]使用基腔讓尾部產生非對稱湍流，減阻達9%;賀銀芝等[10]指出不同后背傾角模型中氣流分離特征差異較大，且阻力值隨后背傾角增大而提高;倪捷等[11]在背部設置溝槽型棱紋仿生結構進行優化，使阻力值降低5%. 這些研究表明，優化尾部特征參數對減阻具有積極意義，但車體結構具有三維特征，以上研究未涉多個參數交互影響作用，因而無法保證優化參數為最優，即未獲得全局最優.

對此，本文以Ahmed模型為研究對象，應用數值仿真模擬，對影響尾部造型的3個主要特征參數進行氣動減阻交互影響研究，并在此基礎上開展全局優化.

1? ?研究方案

1.1? ?原始模型與風洞試驗

本文采用原始斜背角為25°的Ahmed 1 ∶ 1模型開展研究，其基本尺寸如圖1所示（單位：mm）.

為驗證數值仿真方案的精度，對該模型進行HD-2風洞試驗對標驗證，其試驗現場如圖2所示.

1.2? ?原始模型數值仿真與風洞試驗驗證

網格劃分采用四六混合網格（網格縱對稱剖面如圖3所示），網格數量和節點分別達到500萬和200萬. 仿真以ANASYS 14.0為求解器，采用隱式求解、標準壁面函數、二階中心差分法;速度項、紊動能項和紊黏系數項采用二階迎風差分格式. 其外流場仿真邊界條件如表1所示.

按圖3所示的網格模型、表1所示的邊界條件和K-E湍流模型進行數值仿真求解，得到該模型氣動阻力系數Cd為0.305 3;按圖2所示的HD-2風洞試驗所測得的風阻系數為0.298 5，兩者的相對誤差為2.3%，表明了仿真方案的可靠性.

2? ?交互影響研究

Ahmed車型是斜背兩廂車的基本模型，在保證該模型固有主體尺寸不變條件下，后背傾角角度、后背頂部圓角半徑和背部兩側圓角半徑3個參數影響著其流場結構. 為此本文對這3個參數的氣動減阻交互效應進行研究.

2.1? ?影響參數約束條件

1）設后背傾角角度α為特征參數A. 為保持整車造型不發生太大改變，Dumas[12]給出了一個參考范圍，為5°≤α≤40°.

2）設后背頂部圓角半徑為特征參數B. 當α角為40°且圓角倒至后背邊界處時，圓角半徑為812 mm，取整后變量B為50 mm ≤ B ≤ 800 mm.

3）設背部兩側圓角半徑為特征參數C. 根據Cheng[13]的研究，兩側邊緣由棱角變為圓角時，對車輛尾部流場影響最大，為觀察此影響，又考慮到車輛尺寸，變量取值范圍不宜太大，定為10 mm≤C≤100 mm.

3個特征參數示意圖如圖4所示.

2.2? ?試驗設計

為辨識3個特征參數的交互影響規律，采用優化拉丁超立方法生成樣本點來進行試驗設計. 該方法改變了隨機拉丁超立方設計的均勻性，使因子和響應擬合更為精確，且具有非常好的填充空間均衡性. 根據3個變量因子，為減小仿真過程的誤差，提高模擬仿真的準確度，試驗研究中取50組樣本點，依據樣本點生成相應的數字幾何模型，分別對其進行網格劃分和數值仿真計算以獲得氣動阻力系數Cd（數值仿真方案與1.2節相同）.

在整個試驗仿真研究過程中，必須經過參數化幾何建模、網格劃分、CFD流場計算、優化設計等過程，費時費力. 對此，基于UG二次開發實現幾何模型數據交換，以腳本文件對ICEM建立自動網格劃分命令，建立的操作日志文件可實現CFD邊界條件、控制方程和參數調用等功能. 然后在Isight軟件中[14]，采用批處理文件實現幾何模型修改、網格劃分、流體分析計算3個環節的數據調用、啟動、關閉等操作，從而建立高效的集成優化技術. 詳細過程見文獻[15].

2.3? ?交互影響分析

2.3.1? ?阻力的交互影響分析

研究特征參數對氣動阻力影響，轉化為對Cd的貢獻量分析. 分析應分3個層次，即：獨立特征參數變化對Cd的貢獻量、相鄰兩個特征參數變化對Cd的貢獻量交互效應、3個特征參數變化對Cd的貢獻量交互效應.

根據試驗設計樣本進行數值仿真，計算獲得如圖5所示的汽車尾部3個特征參數獨立變化對氣動阻力的一維貢獻百分比Pareto圖. 該圖反映了各變量對響應Cd的貢獻程度百分比，橫坐標為貢獻量百分比，依照不同特征參數的貢獻量絕對值大小，從上至下依次排列. 由圖5可見，特征參數A對氣動阻力的影響為正效應，而特征參數B和C的變化對氣動阻力的影響為負效應. 進一步分析為隨著特征參數A的增大，引起Cd相對增大，正向影響率最大可達51%;特征參數C增大，引起Cd相對減小，最大產生負向影響可達42%;特征參數B產生的負向影響僅為7%.

然而特征參數的獨立變化對Cd的貢獻量分析，僅表征了3種特征參數理想條件下的主次因素，而實際上3個特征參數一旦變化，必然導致造型結構的變化. 因此，應進一步分析3個特征參數之間對氣動阻力Cd的交互效應.

圖6為A、B、C 3個特征參數兩兩之間的交互效應圖. 其中縱坐標為模型的Cd值，橫坐標為各特征參數從低到高的取值，由于3個特征參數間的取值和單位不統一，歸一化后橫坐標無單位量綱. 交互效應圖反映了兩個特征參數交互性對響應Cd的關聯程度，它是在第2個特征參數取不同水平的情況下，分別繪制第1個特征參數對響應的主效應圖，然后疊加而成. 如果交互效應圖中的2條線相互平行，則表示這2個特征參數無交互作用;如果2條線不平行，則表示有交互作用，不平行的程度反映了交互效應的強弱. 由圖6（a）（b）可見，兩條線交叉，且圖6（a）中2條線的不平行性更加明顯，說明A與B、A與C間均存在交互效應，且A與B的交互效應更加強烈，即后背傾角與后背頂部圓角、后背傾角與背部兩側圓角均存在交互效應，且前者的交互效應更加強烈，即后風窗玻璃與上頂部夾角參數引起的Cd變化存在被其余2個特征參數分別引起的Cd變化抵消的交互效應. 圖6（c）為B與C的交互效應圖，圖中2條線沒有出現交叉，說明后背頂部圓角半徑與背部兩側圓角半徑的交互效應較弱.

為進一步分析3個特征參數變化引起的Cd響應，圖7給出了A、B、C 3個特征參數間的交互效應圖，由于是3個特征參數間的交互影響，因此是主效應圖. 由圖7可見，3個特征參數間存在明顯的相互交叉，且縱坐標值隨3個特征參數的變化均為非單調函數，進一步證明了不同特征參數改變時，對風阻系數存在著顯著的此消彼長的交互影響，即說明單一特征參數優化后，并不能獲得氣動阻力全局最優.

2.3.2? ?流場結構影響分析

為了分析3個特征參數變化引起的流場結構變化，圖8為改變單一特征參數而其余兩項保持不變情況下的車身渦流結構（采用Q準則）. 圖8（a）為后背傾角A變化時的尾部流場結構. 由圖8（a）可見，隨著A角度的增大，渦核（深色區域）越來越靠近車輛尾部，縱向渦強度增大，湍流渦結逐漸覆蓋整個背部. 渦核靠近尾部使得壓差阻力增大，縱向渦強度增大又使得阻力減小，在渦核與縱向渦的交互作用下，后背流場結構變得復雜.

圖8（b）為后背傾角為25°，特征參數B變化時的尾部流場結構. 由圖8（b）可見，增大頂部圓角半徑對尾部渦結影響不大，渦核位置及渦結強度無明顯改變. 但圓角抑制了后背氣流分離現象，圓角越大，氣流依附性愈加明顯（如圖8（b）中圈內后背氣流附著面積）.

圖8（c）為后背傾角角度為25°，特征參數C變化時的尾部流場結構.? 由圖8（c）可見，隨著背部兩側圓角半徑增大，氣流順著倒角附著于后背現象明顯，呈現“V”型結構，導致后背壓強增大，“V”字型氣流流至尾部形成兩個旋轉方向相反的縱向渦.

3? ?全局氣動減阻尋優

由上述分析可見，對汽車尾部進行減值優化時，3個特征參數對氣動阻力Cd值有顯著的交互效應. 因此單一參數的優化并不能獲得在保證車身原有造型風格條件下的全局最優值，需要進行尾部的全局尋優.

3.1? ?全局氣動低阻尋優

在進行尾部全局優化時，由于3個特征參數對氣動阻力的影響存在交互效應，因而構建低阻目標函數可能存在多峰性、非線性和不可微性. 梯度優化算法和直接搜索法無法得到全局最優解，因而采用多島遺傳算法尋優，約束條件仍以2.1節中影響參數約束條件為準.

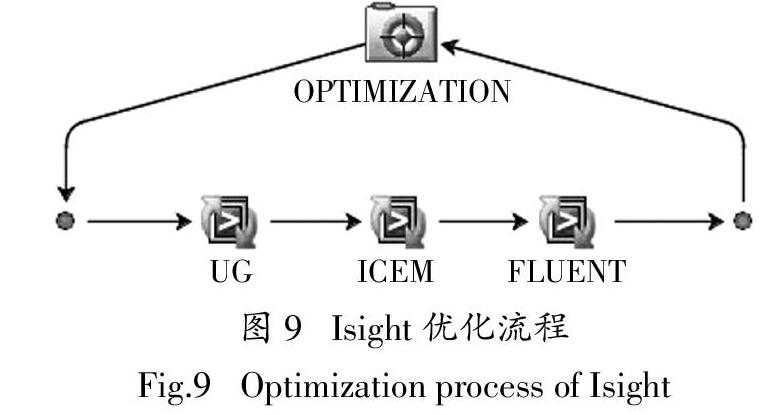
尾部全局氣動低阻尋優以Isight為集成優化平臺，搭建優化流程如圖9所示，優化目標為參數約束條件下的氣動阻力系數Cd最小值，設定種群個數為10，代數為10. 最終尋優結果為：A值為13°，B值為283 mm，C值為58 mm時，氣動阻力系數Cdmin為0.269 4. 此時，對比原始模型，采用全局氣動低阻優化，在尾部關鍵參數最優解集{A，B，C|13，283，58}時，實現減阻11.76%.

3.2? ?優化結果分析

根據在尾部關鍵參數最優解集{A，B，C|13，283，58}重新修改模型，可得尾部全局優化后的模型如圖10所示.

由圖10可見，尾部造型結構相對圓潤，且背部兩側圓角半徑為漸變型. 對尾部全局最優模型與原始模型進行對比，對比的尾渦跡線圖、湍流強度圖、壓力云圖分別如圖11、圖12、圖13所示.

圖11中，原始模型在背部頂角位置處發生氣流分離，而優化后模型氣流流動順暢;從尾部渦結來看，原始模型尾渦渦核位置靠近模型尾部，而優化后模型渦核位置遠離車身尾部，有利于推遲氣流分離以降低氣動阻力.

由圖12可知，圖12（a）中尾部的湍流場強度明顯大于圖12（b）中尾部的湍流場強度，這就意味著優化后的模型湍動能耗散減弱，有利于氣動減阻.

對比圖13原始模型與優化后模型背部車身表面壓力云圖可見，優化后模型的整體表面正壓較原始模型明顯減小，表明壓差阻力減小使得整體阻力降低.

4? ?結? ?論

本文針對汽車尾部結構進行氣動減阻優化時，各幾何特征參數間往往存在此消彼長的現象，使得優化變量盲目而復雜，以Ahmed類車體為研究對象，研究了模型尾部的3個特征參數對氣動阻力交互影響的規律，并應用尾部全局優化計算進行低阻尋優，得到以下結論：

1）后背傾角角度、后背頂部圓角半徑和背部兩側圓角半徑3個特征參數對氣動阻力影響值不同，其中后背傾角角度的減阻貢獻量最大，影響率可達51%;背部兩側圓角半徑影響次之;后背頂部圓角半徑影響最小.

2）后背傾角角度與后背頂部圓角半徑、后背傾角角度與背部兩側圓角半徑特征參數之間，對氣動阻力的影響均具有明顯的交互效應，其中前者的交互效應更加明顯;后背頂部圓角半徑與背部兩側圓角半徑的交互效應較弱. 三者改變對氣動阻力的影響均具有非單調性.

3）在保證原有整體造型風格不變條件下，采用尾部全局優化技術，獲得較佳的后背傾角角度、后背頂部圓角半徑和背部兩側圓角半徑3個參數，可有效抑制背部、推遲尾部的氣流分離，減小壓差阻力，實現最大減阻11.76%.

以上結論為汽車車身造型優化以實現氣動減阻尋優提供了方法與參考.

參考文獻

[1]? ? 谷正氣. 汽車空氣動力學[M]. 北京：人民交通出版社，2005：58-151.

GU Z Q. Automobile aerodynamics[M]. Beijing：China Commu-nications Press，2005：58—151.（In Chinese）

[2]? ? 梁敏，谷正氣，張勇，等. 基于硬點-骨架約束的汽車低阻曲面優化研究[J]. 武漢理工大學學報（交通科學與工程版），2015，39（4）：852—856.

LIANG M，GU Z Q，ZHANG Y，et al. Study of automobile low resistance surface optimization based on hard points-skeleton constraint[J]. Journal of Wuhan University of Technology（Transportation Science and Engineering），2015，39（4）：852—856.（In Chinese）

[3]? ? JOSEPH P，AMANDOL?SE X，AIDER J L. Drag reduction on the 25 slant angle Ahmed reference body using pulsed jets[J]. Experiments in Fluids，2012，52（5）：1169—1185.

[4]? ? WANG X W，ZHOU Y，PIN Y F，et al. Turbulent near wake of an? Ahmed vehicle model[J]. Experiments in Fluids，2013，54（4）：1—19.

[5]? ?WANG H，ZHOU Y，ZOU C. Aerodynamic drag reduction of an Ahmed body based on deflectors[J]. Journal of Wind Engineering & Industrial Aerodynamics，2016，148：34—44.

[6]? ? 張英朝，杜冠茂，朱會，等. 25°Ahmed模型射流主動控制氣動減阻策略[J]. 同濟大學學報（自然科學版），2018，46（1）：100—108.

ZHANG Y C，DU G M，ZHU H，et al. Strategy of active flow control to reduce aerodynamic drag with steady jet for 25° Ahmed model[J]. Journal of Tongji University（Nature? Science Edition），2018，46（1）：100—108.（In Chinese）

[7]? ?THACKER A，AUBRUN S，LEROY A，et al. Effects of suppressing the 3D separation on the rear slant on the flow structures around an Ahmed body[J]. Journal of Wind Engineering and Industrial? Aerodynamics，2012，107/108（6）：237—243.

[8]? ? GRANDEMANGE M，CADOT O，COURBOIS A.A study of wake effects? on the drag of Ahmed's squareback model at the industrial scale[J]. Journal of Wind Engineering and Industrial Aerodynamics，2015，145：282—291.

[9]? ? EVRARD A，CADOT O，HERBERT V，et al. Fluid force and symmetry breaking modes of a 3D bluff body with a base cavity[J]. Journal of Fluids and Structures，2016，61：99—114.

[10]? 賀銀芝，呂越，龍良活，等. Ahmed模型不同后背傾角下的流場及氣動噪聲研究[J]. 同濟大學學報（自然科學版），2017，45（7）：1022—1029.

HE Y Z，L? Y，LONG L H，et al. Investigati-on of flow characteristics and aerodynamic noise for an Ahmed body with different rear slant angles[J]. Journal of Tongji University（Nature Science Edition），2017，45（7）：1022—1029.（In Chinese）

[11]? 倪捷，劉志強，秦洪懋，等. 車輛仿生結構氣動特性分析與優化[J]. 機械設計與制造，2018，3（3）：244—247.

NI J，LIU Z Q，QIN H M，et al. Analysis and optimization on aerodynamic characteristics for a vehicle with biomimetic structure[J]. Machinery Design & Manufacture，2018，3（3）：244—247.（In Chinese）

[12]? DUMAS L. CFD-based optimization for automotive aerodynamics[M]. Berlin：Springer，2008：4—7.

[13]? CHENG S Y. Aerodynamic stability of road vehicles in dynamic pit-ching motion[J]. Journal of Wind Engineering and Industrial Aerodynamics，2013，122：146—156.

[14]? 賴宇陽. Isight參數優化理論與實例詳解[M]. 北京：北京航空航天大學出版社，2012：96—149.

LAI Y Y. Parameter optimization theory and detailed examples[M]. Beijing：Beihang University Press，2012：96—149. （In Chinese）

[15]? 潘正宇，谷正氣，張勇，等. 汽車CFD流場仿真集成高效優化技術研究[J]. 湖南工業大學學報，2018，32（2）：31—37.

PAN Z Y，GU Z Q，ZHANG Y，et al. Research on the simulation integration and efficient optimizati-on of CFD flow field in automobiles[J]. Journal of Hunan University of Technology，2018，32（2）：31—37.（In Chinese）