變上限積分求導定理課堂教學構思設計及實踐效果
楊莉 朱立軍
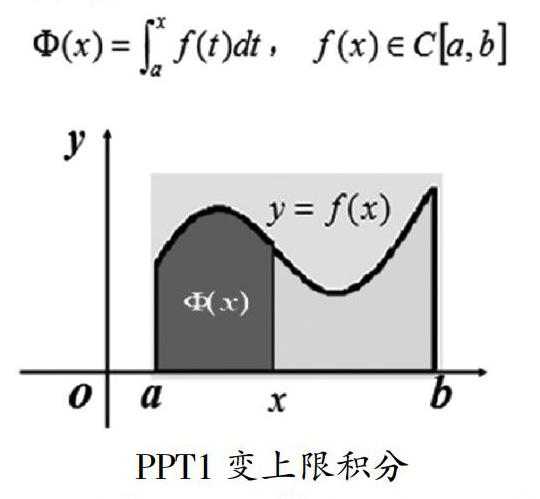

摘? 要:變上限積分求導定理是高等數學教學中的難點,如何使本節課有效的進行,授課教師對其進行了精心的構思:提出問題→解決問題→問題總結→拓展探究,在此過程中融入啟發式、探究式及團隊式教學模式,教學課件豐富,教學語言詼諧,教學互動靈活,教學效果明顯。
關鍵詞:變上限積分;求導定理;課堂教學;構思設計
中圖分類號:G642? ? ? ? ?文獻標志碼:A? ? ? ? ?文章編號:2096-000X(2020)01-0122-03
Abstract: Variable Upper Bound Integrals Derivative Theoremis the difficulty inCalculusteaching.To make this lesson effective, the teacher carefully designed it by following steps: ask questions,answer questions,summarize questions and expand inquiry. Heuristic, inquiry and team-based teaching modes are adopted in the process, which obtain rich teaching courses, humorous teaching languages, flexible teaching interaction and obvious teaching effects.
Keywords: Variable Upper Bound Integrals; derivative theorem; classroom teaching; conceptual design
《高等數學》是我校理工類和經管類的專業基礎課,既能展現基礎學科的理論特色又能兼顧專業課程的實踐特色,同時也是學生學習其他后繼課程的基礎,在人才培育中占有重要地位。通過該課程的學習,能很好的培養學生的抽象思維能力、邏輯推理能力、空間想象能力、運算能力以及綜合運用所學知識去分析和解決實際問題的能力。
如何提高高等數學的教學質量,已經成為《高等數學》教學活動中亟待解決的課題。對于民族院校經濟類專業《高等數學》教學,需考慮學生的生源及個體差異性,對教學過程的設計需精心構思,目的激發學生對高等數學課程的積極性和熱愛程度,使其一環緊扣一環的繼續學習高等數學后續知識,并且更重要的是在數學課程中培養學生積極正能量的人格品質,從而為少數民族地區培育有用的服務型人才。
變上限積分是高等數學中聯系不定積分與定積分的一個重要概念,其教學設計構思關系著整個教學效果的整體呈現。以下為變上限積分教學構思設計過程與實踐效果。
一、承前啟后,有效導入
全體同學請將你的美麗目光集中在這里(手勢右手大展繞一圈指向左手手心,提示大家注意),同學們,早上好!
今天我們一起來探討學習第6章定積分6.4節微積分基本定理之變上限積分求導定理。
上節課,我們提出了兩個問題。
問題1:我們已經系統的學習了一元函數的微分學、初步的學習了積分學,我們要問:這兩者之間是否有一定的聯系呢?如果有,能說明什么問題?
問題2:截至目前,求定積分只能通過定義,然而定義中的和式極限給計算帶來了一定的繁雜性,那么要問:是否有一種更巧妙簡便的辦法來計算定積分?
為此,我們引入了變上限積分。
通過拉窗簾活動,由已知(定積分)到未知(變上限積分),自然過渡到變上限積分的定義。
進入PPT:
一、變上限積分
觀察這個式子'(x)=f(x),認識一下?椎(x)和f(x)的關系。f(x)是?椎(x)的導函數,?椎(x)是f(x)的原函數。那也就是說在[a,b]上連續的函數f(x)必然存在原函數,下面以定理的形式給出。
PPT4變上限積分求導定理
變上限積分求導定理回答了上節課我們提出的第1個問題微分學與積分學的聯系,它是溝通微分學與積分學的橋梁。同時說明了變上限積分的導數等于被積函數在上限處的函數值,也表明了閉區間上的連續函數必然存在原函數,而且這個原函數是由其本身生成的變上限積分函數。
趁熱打鐵,我們利用定理1求幾個變上限積分的導數。
定理1是我們這節課的終極目標,目的達到,課程到此結束。
四、梳理總結,拓展探究
下面我們來簡單梳理總結一下本節課。
由上節課提出的兩個問題我們引入變上限積分,本節課比較嚴謹的分析推導變上限積分求導定理。在分析過程中遇到兩個有趣的疑難點:
(1)? ? ? ? ? ? ? ? ? 復雜問題簡單化;
(2)? ? ? ? ? ? ?,將變量為?駐x→0時的極限轉化為變量為?孜→x時的極限,問題簡易化。
這也就是說我們在遇到困難時,一種辦法行不通,我們得大膽嘗試、探索尋求另一種方法來解決,那么我們想要的那個美麗的答案馬上會得到。正所謂宋代詩人陸游《游山西村》中的一句詩所說“山重水復疑無路,柳暗花明又一村”。
下面布置作業,課下同學們可以試著完成兩個任務。注:課下作業任務2同學們在“學習通”主題討論中互相討論;任務3的WORD編輯上傳到“學習通”作業(在線課程任務)中。
PPT5課下作業
五、實踐效果,問卷呈現
本節課于管理學院選修《高等數學》班級進行,通過對39名學生進行問卷調查(參見文獻[5]),整體教學效果良好,抽選問卷(共12個問題)中的4個問題如下。
參考文獻:
[1]同濟大學數學系.高等數學(第六版):上冊[M].北京:高等教育出版社,2006.
[2]趙樹嫄.微積分(第四版)[M].北京:中國人民大學出版社,2016.
[3]肖俊.關于變上限函數求導的教學實例[J].高等數學研究,2013,16(06):49-51.
[4]變上限積分函數動態圖[EB/OL].http://img.bimg.126.net/photo/KEf5qTFJDxB_ovLzLHL7mQ==/4224376450474286368.jpg.
[5]6.4節微積分基本定理之“變上限的定積分”求導定理教學效果測評問卷調查[EB/OL].http://mooc1.chaoxing.com/course/202227494.html

