貴州省學生肺結核流行趨勢分析及預警系統建立

貴州省疾病預防控制中心結核病防治研究所（貴陽550004）

結核病是由結核分枝桿菌感染引起的慢性傳染病，是一種古老而常見且嚴重危害人類健康的慢性傳染性疾病之一，結核菌可能侵入人體全身各種器官，但主要侵犯肺臟，是我國重要的公共衛生問題之一，結核病患者數居全球第二位，2018年WHO 估算[1]，我國2017年結核病新發患者數為88.9萬，發病率為63/10萬，結核病死亡數為3.7萬例，死亡率為2.6/10萬，是全球第二大結核病高負擔、高疫情國家。貴州省是我國結核病疫情較高的省份之一，我省每年報告的肺結核患者中排在第二位的是學生，提示，學生是易感人群，應作為我省結核病防控工作的重點人群[2]。求和自回歸移動平均（autoregres-sive integrated moving average，ARIMA）模型常用于預測傳染病的短期發病趨勢，預測對象可隨時間變化而形成數據序列，隨機變量是一組依賴于時間t的，這組隨機變量所具有的自相關性被相應的數學模型描述出來，表征了預測對象發展的延續性，就可以從時間序列的過去值及現在值預測未來的值，ARIMA 模型對于我國開展肺結核發病率預測預警工作具有重要指導意義[3]。本研究采用ARIMA時間序列預測模型，分析貴州省2013年1月至2017年12月學生肺結核發病數據，預測2018年學生肺結核發病的變化趨勢，并與2018 數據進行對比，從而探索我省學校結核病報告發病預測的新方法，探索學生肺結核發病的預測模型，這對早期采取精準有效的防控措施，在節約人力、物力、財力的基礎上同時為今后學校結核病防控工作中提供科學理論參考依據均具有重要意義。

1 資料與方法

1.1 資料來源2013年1月1日至2017年12月31日肺結核報告發病數的資料來源于“結核病管理信息系統”，人口資料來源于《貴州年鑒》。

1.2 方法

1.2.1 數據整理根據“結核病管理信息系統”和《貴州年鑒》收集相關數據，并按照年、月份歸類整理。

1.2.2 建立ARIMA 模型

1.2.2.1 繪制時間序列圖 根據2013-2017年貴州省學生肺結核月發病數據繪制時間序列圖，初步確定p，d，q和P，D，Q的值是通過計算自相關系數（Autocorrelation Function，ACF）和偏自相關系數（Partial Autocorrelation Function，PACF），從而分析序列平穩性。

1.2.2.2 模型擬合 采用SPSS 19.0 軟件中的“專家建模器”中選擇“ARIMA 模型”對模型反復擬合分析、比較；通過分析擬合篩選出最優模型，比較的主要指標有平穩的R2（該統計量用于比較模型中的固定成分與簡單均值模型的差別，該值越高則擬合越好）、R2（該統計量表示模型所能解釋的數據變異占變異的比例）、正態化BIC（該統計量基于均方誤差統計量，并考慮了模型的參數個數和序列數據個數）。

1.2.2.3 預測預警分析 通過模型的反復修正和改進后篩選出擬合度最優模型，并應用此模型對貴州省學校結核病發病率進行預測和預警分析。1.3 統計學方法 學生肺結核病例資料用WPS Office 建立數據庫，采用SPSS 19.0 統計學分析，計算2013-2017年各年度學生肺結核報告發病率，進行趨勢分析，檢驗水準α=0.05。

2 結果

2.1 總體情況2013-2017年貴州省共報告學生肺結核20 620例，年均報告發病數為4 124例，年均報告發病率為46.01/10萬，學生肺結核報告發病率差異有統計學意義（χ2= 345.677，P＜0.001）。見表1。

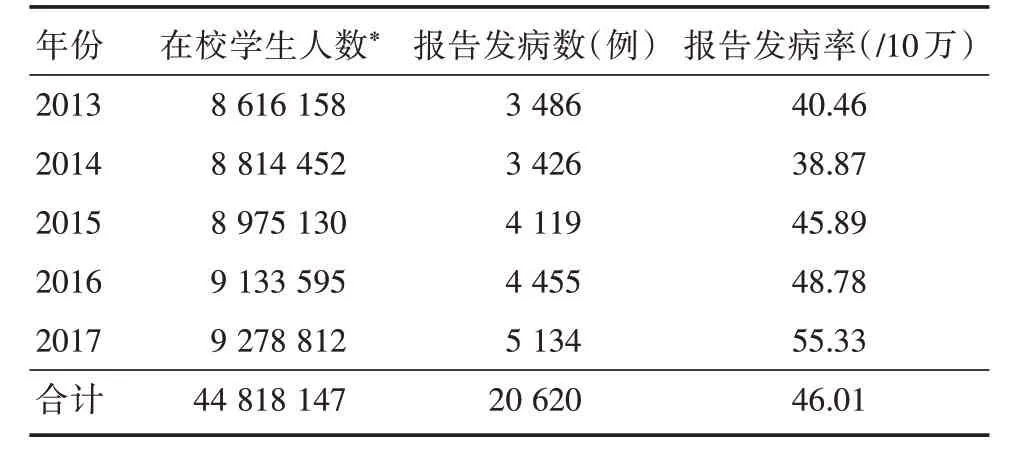
表1 貴州省2013-2017年學生肺結核報告發病情況Tab.1 Reported incidence of tuberculosis among students in Guizhou Province from 2013 to 2017

2.2 模型識別

2.2.1 繪制時間序列圖繪制2013-2017年全省學生肺結核報告發病數的時間序列圖（圖1），總體無上升和下降趨勢，月發病數主要集中在187～688例，平均343.7例，顯示發病數是隨時間變化而變化的，呈季節變化的趨勢關系，以年為周期，每年發生相似的變化，表現為冬春季升高，夏秋季下降，序列的平均水平波動較大，說明該序列為非平穩的時間序列。

2.2.2 初步確定模型參數通過對序列進行12 步差分處理可能達到有效控制序列的長期趨勢和季節周期性，原序列經1 階差分后為平穩序列（圖2），初步確定模型ARIMA（p，d，q）（P，D，Q）s中參數d=1，D=1。該序列具有連續相關性和季節性，季節以12個月為周期，在“專家建模器”的條件設置中選擇的兩種模型均考慮復合季節模型。2.3 參數估計 模型參數估計運用最大似然估計（maximum likelihood estimation，MLE）或者最小二乘法估計（least squares estimation，LSE），本研究采用最大似然估計，獲得模型ARIMA（p，d，q）（P，D，Q）s 中的p、q、P、Q 參數，經差分后，繪制序列的自相關系數圖（ACF）和偏自相關系數圖（PACF）（圖3）。在SPSS19.0 軟件中，依次給參數p、q、P、Q分別賦值，根據每次賦值后的參數差異有無統計學意義來判斷模型擬合情況，從而確定模型參數。

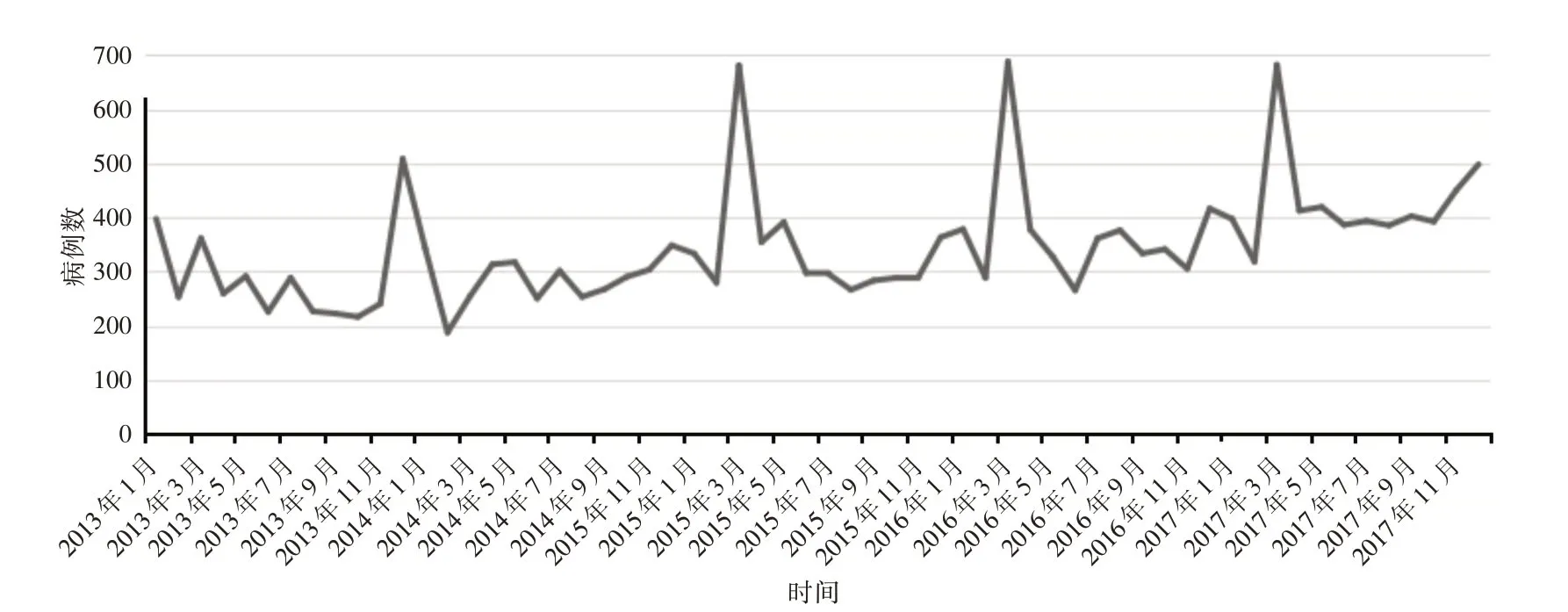
圖1 2013-2017年貴州省學生肺結核按月發病數時間序列圖Fig.1 Time series of monthly incidence of tuberculosis among students in Guizhou Province from 2013 to 2017

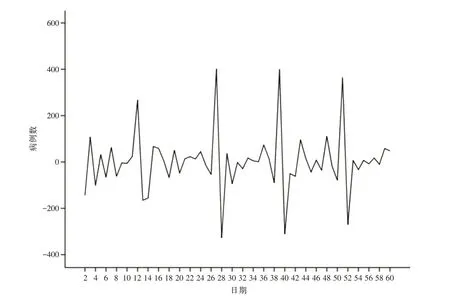
圖2 2013-2017年貴州省學生肺結核原序列經差分后時間序列圖Fig.2 Time series after differential analysis of the original sequence of tuberculosis in Guizhou students in 2013-2017

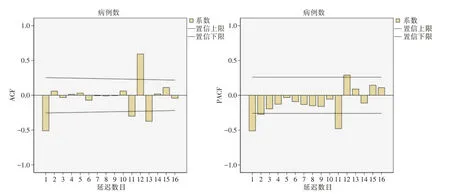
圖3 原序列經差分后ACF和PACF 圖Fig.3 ACF and PACF of the original sequence after difference

圖4 殘差ACF和PACF 圖Fig.4 Residual ACF and PACF

2.4 模型診斷經過不斷篩選反復擬合，篩選出擬合度較好的2個模型是ARIMA（0，1，0）（0，1，0）12和ARIMA（0，1，1）（1，1，0）12，從ARIMA（0，1，0）（0，1，0）12模型的擬合值和實際值較接近，因此是擬合度最好的模型（圖5-6）。從擬合度檢驗結果看，雖然2個模型的固定R2均大于0，但ARIMA（0，1，0）（0，1，0）12模型的平穩R2和R2更接近1，分別是0.842、0.842，統計量、模型參數差異具有統計學意義，擬合度較好。見表2。

2.5 預測與檢驗經過擬合度檢驗，選擇ARIMA（0，1，0）（0，1，0）12模型作為預測模型，預測我省2018年學生肺結核報告發病絕對數。通過預測結果提示，報告發病高峰在3、10和9月，以95%CI的上限作為預警指標，本研究年度預警值為5 417例。見表3。

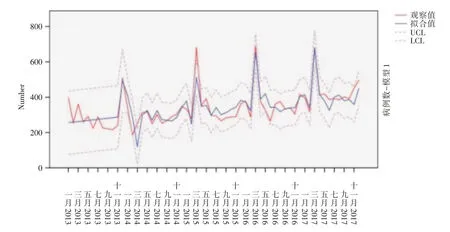
圖5 2013-2017年學生肺結核發病數ARIMA（0，1，1）（1，1，0）12模型擬合圖Fig.5 ARIMA（0，1，1）（1，1，0）12 model fitting chart of tuberculosis incidence in 2013-2017

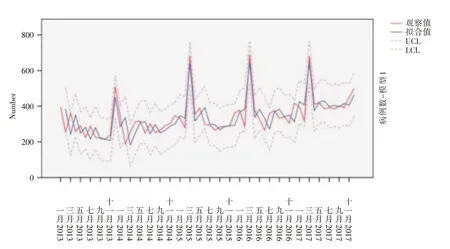
圖6 2013-2017年學生肺結核發病數ARIMA（0，1，0）（0，1，0）12模型擬合圖Fig.6 ARIMA（0，1，0）（0，1，0）12 model fitting chart of tuberculosis incidence in 2013-2017

表2 學生肺結核發病入選模型擬合度檢驗結果Tab.2 Test results of fitting degree of selected model of tuberculosis incidence in students

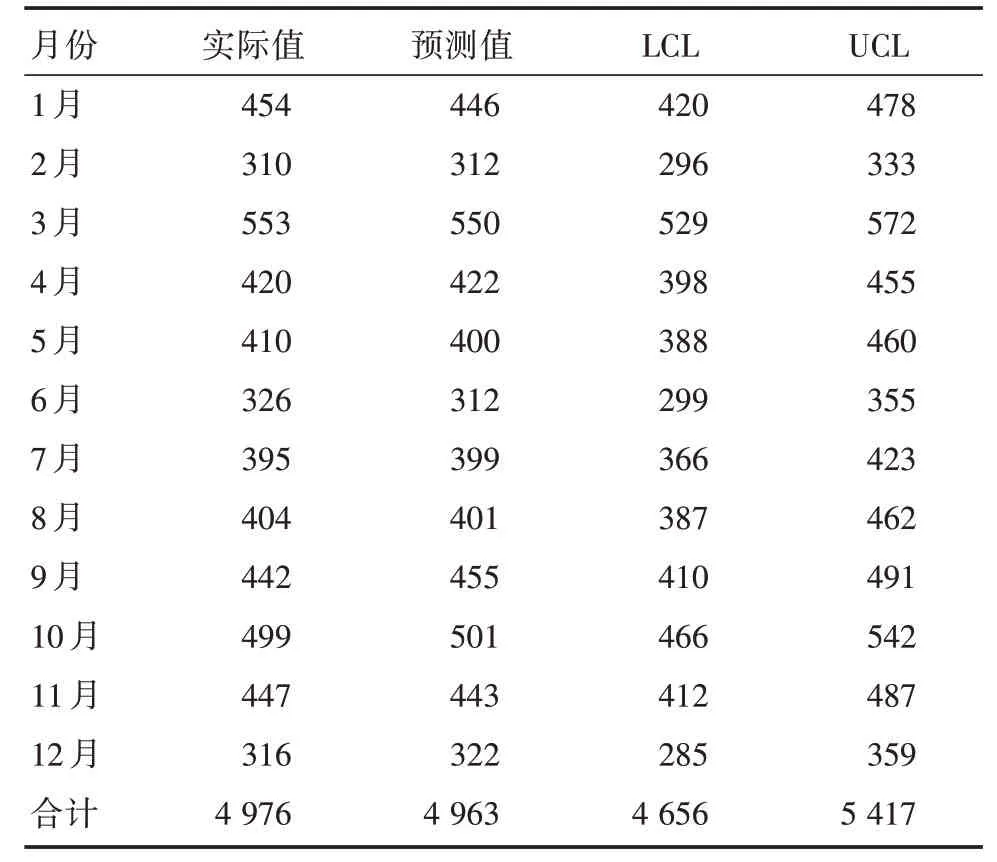
表3 ARIMA 模型預測2018年貴州省學生肺結核發病數Tab.3 ARIMA model predicts the incidence of tuberculosis among students in Guizhou Province in 2018

3 討論

學生肺結核預測在學校結核病防治工作中具有重要意義，因此選擇精確的預測方法至關重要[4]。ARIMA是一種靈敏度較高的序列分析預測模型，在傳染病發病率的預測中應用較廣泛[4-7]。本研究采用2013-2017年貴州省學生肺結核報告發病數建立ARIMA 預測模型，通過反復篩選后確定適合的模型為ARIMA（0，1，0）（0，1，0）12，初步建立我省學生肺結核較敏感的發病預測模型，以期早期發現疫情并及時采取處置措施，防止疫情擴散，對學校結核病防控工作達到預警作用。結果顯示，2013-2017年的實際數與模型擬合數基本一致，實際數均在95%置信區間內，模型對2018年每月學生肺結核發病數的預測值與實際報告發病數進行比較，提示本研究建立的模型基本合理。

學生是我省結核病防控的重點人群之一[8]。本研究學生肺結核的年均報告發病率為46/10萬，高于廣西[9]13.06/10萬、浦江[10]17.56/10萬，低于西藏[11]84.56/10萬，年度發病率差異有統計學意義，2017年的發病率比往年有明顯增高，提示我省學生肺結核總體疫情仍不容忽視，提高學校結核病聚集性疫情可能發生的警惕性，應加強我省學校結核病防控工作。

學校的特點主要是人口密度較大、學生接觸密切，而且學習氛圍較緊張、學生抵抗力降低等可能發生流行。肺結核不僅影響學生的身心健康和學業造成影響，也可能給家庭宿舍、校園健康和社會穩定帶來不良影響[12]。研究顯示，肺結核報告發病數隨時間變化的趨勢關系，波動有一定的季節變化，冬春季升高，夏秋季下降，與全國發病和報告高峰基本一致[13]。從時間序列圖看，3-5月是發病高峰，其次是12-2月，可能春季多是畢業生體檢高峰，冬春季天氣較濕冷，教室、宿舍等人口密集的公共場所通風不良等因素有關。同時，可能由于學習負擔重，尤其是畢業生，作息時間不規律、飲食營養攝入不足、體育鍛煉減少等原因使學生身體抵抗力降低[12]；也可能與每年全省開展“3·24世界結核病防治日”的宣傳活動有關。因此，不斷完善結核病患者的發現機制，統籌合理配置醫療資源，不斷提高醫療機構服務能力是重要策略，也是降低結核病疫情的必要措施[14]。

本研究采用的是肺結核學生病例建立、分析并篩選出最優預測模型，從而對2018年發病絕對數進行預測，95%CI的預測上限可作為學生肺結核可能出現異常、聚集性、暴發等預警指標，提示，報告發病數出現異常值可能造成暴發或流行，但也可能與防控策略、患者發現、診療和服務模式、診斷標準和數據填報等有關，或者是其他社會事件的影響[9]。KUANG 等[15]也認為，與潛伏期長的傳染病相比，潛伏期短的傳染病靈敏度低，但更能及時發現暴發。因此，應充分理解時下與防控措施相關的政策性文件、新出臺的肺結核診斷標準和可能的社會事件等綜合對異常值進行判定，排除非疾病本身的因素后，結合現場流行病學調查和分子流行病學分析[16-18]，在對疫情性質和傳播模式進行定性時應采取相應的防控干預策略。ARIMA 模型隨著時間的延長，預測誤差會增大，但總體來說預測準確性較高[14]，但預測值與實際值仍存在一定的偏差[19]，本研究的預測值和實際值存在一定的差異，ARIMA 模型更廣泛應用于短期預測，相關研究也顯示[20-21]，隨著時間的延長，觀察對象不斷增加，在實際工作中需要提高監測工作質量，持續更新修正模型，才能獲得更加準確而實用的預測結果。

本研究的模型是針對全省監測數據，數據質量可靠程度直接關系預警系統的有效性，這對縣級定點醫院結核門診醫師在詢問、錄入信息時確保學生信息的準確性具有較高要求，嚴格按照健康檢查、轉診、追蹤等正確信息錄入。今后可以考慮各縣區根據當地數據建立模型，不斷提高模型預警的敏感性、及時性和準確性。