任意地基系數下閉合框架結構變形計算探討

摘 要 結構設計中常采用荷載結構法和地層結構法，本文主要采用后者，選取多種不同的地基系數，進而探討任意地基系數結構的內力以及變形特點，從而優化結構設計。

關鍵詞 結構荷載法;任意地基系數;變形計算

引言

城市地下空間的開發和利用是造福后代的新型資源儲備和手段。地下空間的使用在某些方面上緩解了城市土地資源壓力，在一定程度上解決了資源紛爭，是城市未來重要發展方向之一。

目前地下結構設計中，常采用荷載結構法和地層結構法[1-2]，前者的基本理論體系為結構力學原理，計算快捷，應用廣泛;后者依托于計算機的各種有限元軟件進行數值模擬計算，可以模擬地下結構的開挖過程，但對于參數的要求嚴格且計算復雜。本文主要兼顧以上兩種設計方法，采用控制變量法，簡要分析任意地基系數結構的內力以及變形特點。

1工程實例

本文以某一地下結構工程為例，依據其工程概況和地質條件獲取計算條件如下：該結構凈寬 12m，凈高9m，底板厚度500mm，側板厚度500mm，結構頂板厚度500mm，埋深為5m。采用鋼筋混凝土結構，其平面形狀為矩形，淤泥質黏土為主，混凝土彈性模量E=2.95Gpa，開挖面以上無活荷載。荷載主要考慮結構自重及圍巖壓力。

2參數選取

2.1 物理力學參數

其材料物理、力學指標如下：鋼筋混凝土容重25KN/m3彈模29.5Gpa，泊松比0.2。土體重度17.3KN/m3，黏聚力9.6Gpa，內摩擦角9.1°，荷載考慮結構自重及圍巖壓力。

2.2 荷載計算

（1）作用在結構上的荷載

①頂板永久荷載：

考慮結構自重

②地層豎向土壓力：

由于埋深15m

（2）底板上永久荷載

①底板自重：

（3）結構剛度：

（4）結構截面彎矩：

（5）彈性模量：

3計算分析

3.1 模型建立

運用Feon有限元法去求解，在程序起始條件中輸入混凝土彈性模量E1=2.95GPa、寬度為單元1的情況下截面面積A=0.5m2、截面設計厚度為500mm，則計算出支撐慣性矩為I=0.0104m4、結構剛度EI=3.068×106N/mm。參數輸入完畢后，將建立的模型輸入其中，假設結構側面區域為彈性抗力每隔0.5m設置彈簧則包括坐標點（0，-i*0.5），i∈[0，18]。結構底部考慮彈性抗力為常數每隔一米設置一個彈簧包括坐標點（0，-9.5）至（12，-9.5）共12點，考慮彈簧長度為0.5m，故考慮以上坐標點及參數并進行模板化可以得到如下圖3.1的結構計算模型。

在計算常數模型變形及內力的時候，假設地下結構的底部彈性抗力為固定值15000KN/m2，且依次考慮結構側面的彈性抗力為（a）沿深度呈常數分布、（b）沿深度呈梯形分布、（c）沿深度呈拋物線（上小下大）分布三種形式，分別進行計算。

3.2 相關計算分析

（a）情形：假設地基系數為常數，K1=15000KN/m，K2=10000KN/m，其內力和變形計算結果如下圖3.2所示。（Mz為彎矩、Ty為軸力、N為剪力下同）。

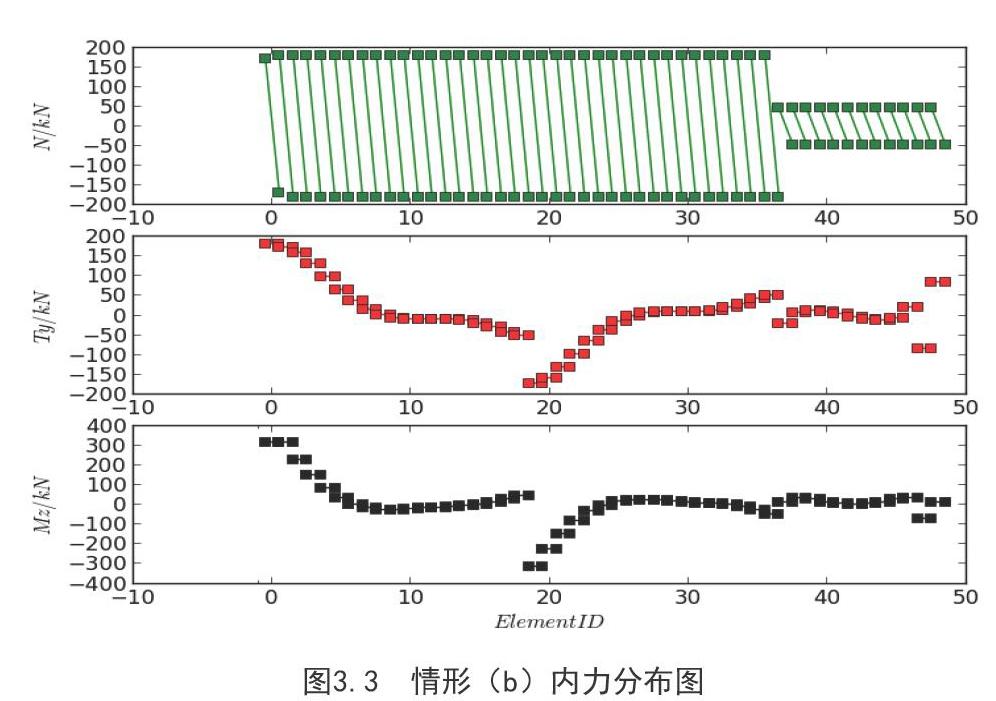
（b）情形：假設地基系數為線行分布在結構區域內最小值Kmin=5000KN/m，最大值Kmax=15000KN/m，地基系數函數表達式為Y=10000/9*X+5000，其內力和變形計算結果如下圖3.3所示。

（c）情形：假設地基系數為二次分布在結構區域內存在最大值Kmax=15000KN/m，拋物線方程為Y=43.2x2+500x+7000，其內力和變形計算結果如下圖3.4所示。

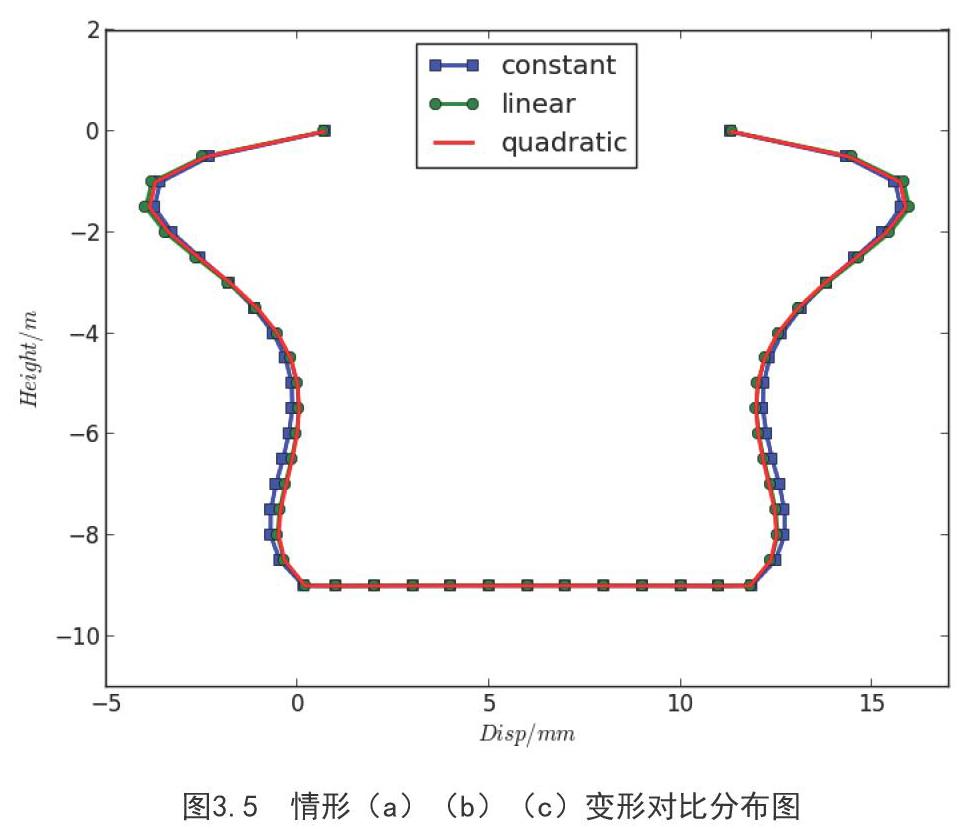
若采用將三個變形分布圖置于一個程序中，即可獲取不同情形下的變形對比分析圖，如圖3.5所示。

3.3 結果與分析

由以上計算結果分析可知：

（1）地基系數常數型分部下結構的變形

在常數型地基系數下，墻體變形情況在頂部是變形最小的，僅在4.0mm-4.5mm之間。結合圖3.2.7得知：在地基系數為常數的情況下，其彎矩是三者之間最大的。由于結構頂端的約束，導致了位移在三者之間最小。在區域y∈[0，-2]之間達到最大變形，即使在結構的約束下，但是變形仍在增大。在y∈[-2，-5]時發生變化，變形逐漸收縮;在基坑底部y=-5之后，變形又開始變化且在y=-8時達到最值，并隨后發生收縮。因此在設計該結構的時候，應該考慮到此問題，對變形較大位置重點支護，保證基坑開挖的過程中，能盡量控制好結構的變形且不影響施工的進程以及周邊環境。

（2）地基系數線性分部下結構的變形

在線性地基系數，墻體變形在y=-1.5時達到最值，約5mm;結構整體變形在y<-1.5時呈為遞減趨勢。表明在該地基系數的情況下，變形會隨著土層的加深而變小，且在此之后的變形接近于常數分布，但總體上要小于常數分布變形。

（3）地基系數二次函數分布下結構的變形

拋物線型地基系數的變形情況介于（a）（b）情形之間，其頂部變形趨勢與常數型地基系數變化一致，但結構變形都小于常數型地基系數下結構的變形。其變形最大值與整體變形差距較小，且在結構底部達到最小值，與直線型的差距不明顯，也就是說這種假設情況的計算，可能處于常數型和直線型之間，與兩者都有一定的相似度。

3.4 其他模型

（1）具體計算方法。①相對剛度較大，視地基反力為線性分布，并作為荷載作用于底板，用變形法求解。②相對剛度較小，視為的彈性地基上閉合。結構：先用力法進行結構分離，然后分別用變形法和彈性地基梁求解。

（2）地基反力分布假設。①反力按直線分布;中間大兩側小和兩側大中間小。②反力強度與各點地基沉降量成正比分布。③地基為半無限彈性體，按彈性理論計算反力。

在本文所采用的荷載結構法中影響結構變形的因素不僅僅是地基系數，同樣還有基地彈性反力、彈簧剛度、彈簧長度、彈簧的分布等其他相關因素都可以改變結構的變形。由于論文篇幅的原因再次不加以詳細描述。

4結論與展望

4.1 結論

（1）荷載結構法就是將圍巖和結構分開考慮。在荷載結構法中，周邊巖土體向結構施加各種主動荷載，且巖土體對結構有一定的彈性抗力以約束結構變形，彈性抗力在計算中模擬為彈簧。由于荷載結構法相對來講設計思路清晰，計算簡潔，甚至有些計算可以不運用計算軟件，所以它是目前設計人員常用的設計方法。

（2）通過計算發現在地基系數中，“常數”值法在結構變形的情況中，如果從安全的角度，確保結構的變形不足以影響施工進程與周圍環境的情況的時候，可以假設地基系數為“常數”的計算方法進行計算。

（3）整個計算的過程和三個計算結果與多個實際工程結構變形的情況對比，發現二次元系數值法的計算結果與實際變形情況相似度更高，表明二次元系數值法靈活的適用于地層地基系數多變的情況下，也就因此二次元系數值法具有廣泛的適應性。

（4）通過計算結果在圖中的對比，發現線性函數系數值法的變化趨勢，以及最值處于常數值系數法和二次元系數值法之間，與兩者的變化趨勢都有一定的相似度，所以在設計結構的時候，假設地基系數這樣分布可以進行更經濟的結構設計。

4.2 展望

荷載結構法由于計算簡便，受地層參數浮動變化的影響不是很大，結構設計常采用。本文重點研究了在不同地基系數下的結構變形以及內力，并得到了一些結論，但仍有問題有待解決和改進：

（1）以更科學和更具有代表性的經驗來完善經驗類比法的內容，切忌按照傳統經驗閉門造車。未來的研究方向可以在如何盡情地利用圍巖的承載能力上發展，從而使施工設計更加環保經濟安全。

（2）根據實際情況以最科學的方法選用合理恰當的計算方法，而不是單純的以計算簡便為主。這樣可以把計算結果更精確化穩定化。

參考文獻

[1] TB 10003-2005.鐵路隧道設計規范[S].北京：中國鐵道出版社，2006年.

[2] 施仲衡.地下鐵路設計與施工[M].西安：陜西科學技術出版社，2006：39.

作者簡介

梅新（1987-），男，湖北安陸人;學歷：碩士研究生，工程師，現就職單位：中鐵第四勘察設計院集團有限公司，研究方向：從事地鐵監測工作。