廣義矩陣代數上的一類局部非線性三重可導映射

費秀海，戴磊，朱國衛(wèi)

（1.滇西科技師范學院 數理學院，云南 臨滄677099； 2.渭南師范學院 數學與統計學院，陜西 渭南714099）

1 預備知識

設Α 是含有單位元的交換環(huán)R 上的一個代數,P 為Α 中 的 一 固 定 元,是Α上的一個可加(或無可加性假設)的映射。若對任意的X ∈Α 且2X =0, 有X =0, 則稱Α 是2-無撓的。若對任意的X,Y ∈Α 且XY =P, 有

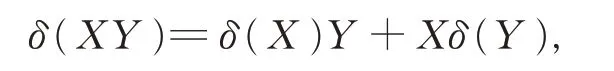
則稱δ 是一個P 點可導映射(或P 點非線性可導映射)；若對任意的X,Y ∈Α 且XY =P, 有

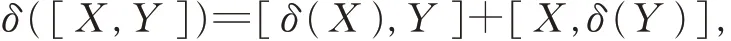
則稱δ 是一個P 點Lie 可導映射(或P 點非線性Lie可導映射)；若對任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

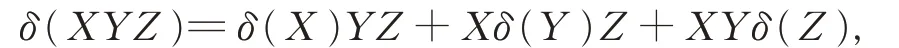
則稱δ 是一個局部三重可導(或局部非線性三重可導)映射。

近年來,算子代數上各種類型的映射吸引了研究者的興趣,并成為了算子代數研究領域的熱點問題。文獻[1-3]分別研究了套代數、三角代數、廣義矩陣代數上的全可導點、Jordan 高階全可導點及交換零點Jordan 可導映射；文獻[4-5]刻畫了素環(huán)和B(Χ)上的非線性Lie 可導映射；文獻[6-10]主要研究了三角代數上的Lie 導子、非線性Lie (高階Lie)可導映射、非線性廣義Lie 可導映射；文獻[11-12]將非線性和局部非線性結合起來研究了上三角矩陣代數和全矩陣代數上的非線性零點可導映射。特別地, 孟利花等[13]研究了三角代數上的局部非線性三重可導映射。本文主要研究廣義矩陣代數上的局部非線性三重可導映射。

下文中將用到的關于廣義矩陣代數的基本概念及性質介紹如下：

設Α 和Β 是含有單位元的交換環(huán)R 上的代數,Μ 是 忠 實(Α,Β)-雙 邊 模, Ν 是 忠 實(Β,Α)-雙 邊模, 則

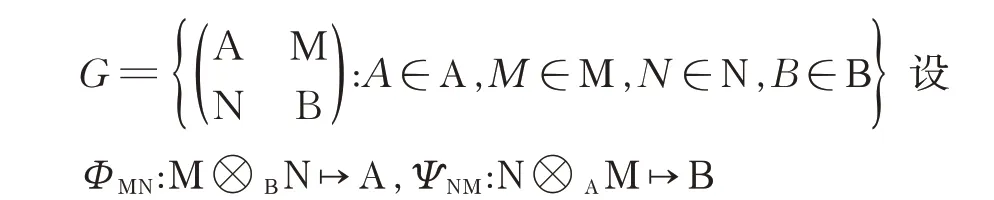
是雙邊模同態(tài),且滿足交換圖:

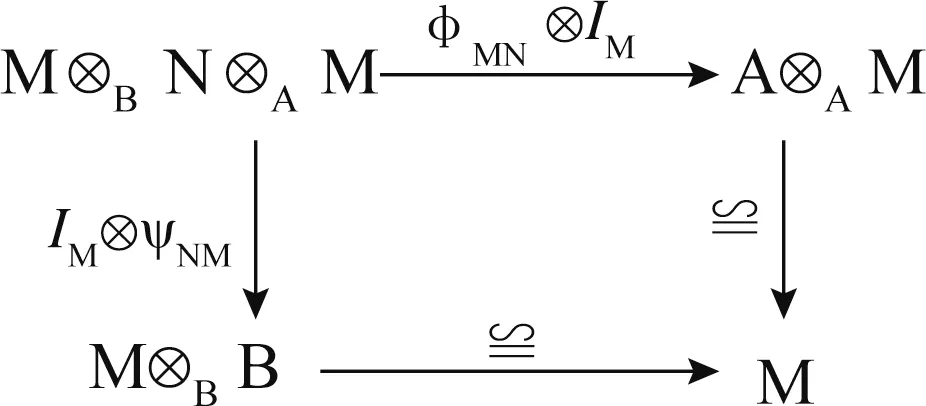
和

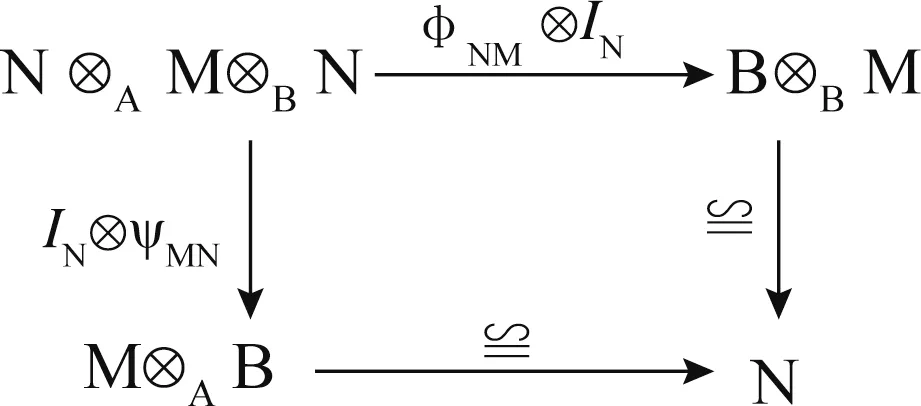
則按矩陣通常的加法和乘法運算構成結合代數，稱G 是一個廣義矩陣代數。當Ν=0 時,稱G 是一個三角代數。

設1Α和1Β分別為代數Α 和Β 中的單位元, 1 是廣義矩陣代數G 中的單位元。

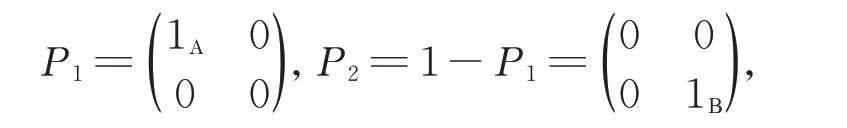
由 于 G11=P1GP1, G12=P1GP2，G21=P2GP1，G22=P2GP2是G 的子代數且分別同構于Α, Μ,Ν和Β, 從而廣義矩陣代數G 在雙模同構意義下可被分解為

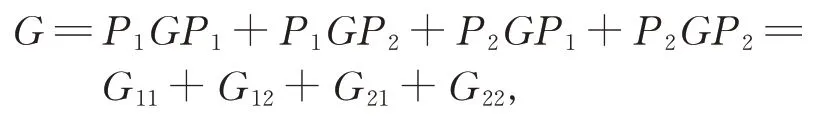
進而對任意的矩陣X ∈G, 可將X 分解成

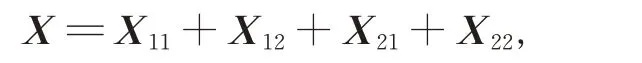
其中，Xij∈Gij, 1≤i,j ≤2 。

2 主要結論及證明

定理1設G 是一個2-無撓的廣義矩陣代數,Ω={T ∈G:T2=0}，且φ 是G 上 的 一 個 映 射(無 可加性假設), 若對任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

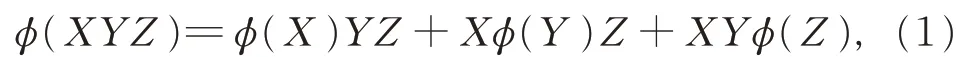
則φ 是一個可加的導子。

為證定理1, 需要以下引理。

引理1對任意的1≤i ≠j ≤2,有

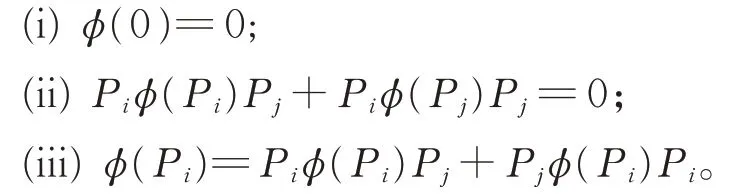
證 明在 式(1) 中, 令X =Y =Z=0, 有φ(0)=0。在 式(1)中,令X =Y =Pi，Z=Pj(1≤i ≠j ≤2), 則有

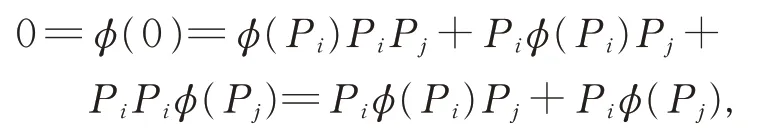
進而可得

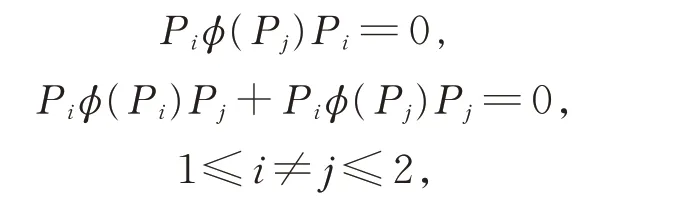
在式(1)中，令X =Y =Pi，Z=Xij∈Gij，則有

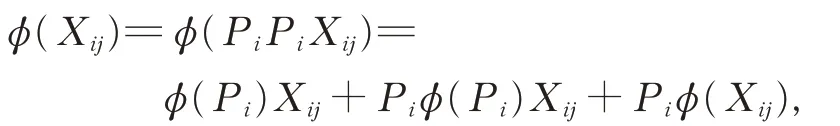
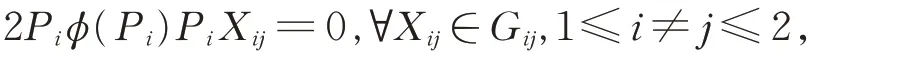
可得從而由Gij（1≤i ≠j ≤2）的忠實性,有

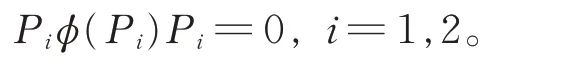
證畢。

注1令X0=P1φ(P1)P2-P2φ(P1)P1，對任意的X ∈G，定義映射δ:G ?G 為

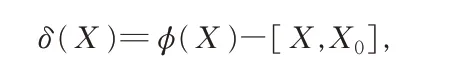
則δ 也是一個局部非線性三重可導映射，即對任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

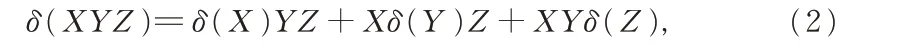
且由引理1 容易驗證δ(P1)=δ(P2)=0。

引 理2對 任 意 的Xij∈Gij（1≤i,j ≤2）,有δ(Xij)∈Gij。

證明對任意的Xii∈Gii，一方面在式(2)中，令X =Xii， Y =Z=Pj（1≤i ≠j ≤2） ， 由 于δ(Pj)=0，從而有δ(Xii)Pj=0，進而有

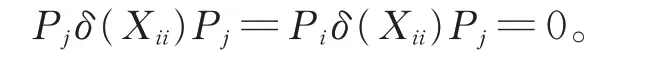
另一方面在式(2)中，令X =Pj,Y =Xii,Z=Pi（1≤i ≠j ≤2），可得Pjδ(Xii)Pi=0,從而δ(Xii)∈Gii。

對任意的Xij∈Gij（1≤i ≠j ≤2），在式(2)中，令X =Pi,Y =Xij，Z=Pj，可得

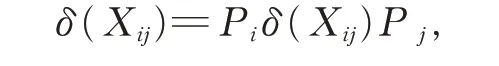
從而δ(Xij)∈Gij。

證畢。

引 理3對 任 意 的Xii∈Gii,Xjj∈Gjj,Xij∈Gij（1≤i ≠j ≤2）,有

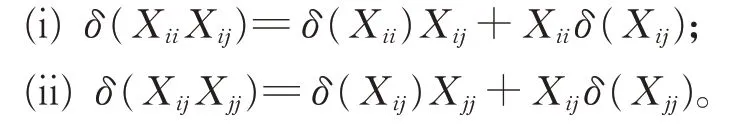
證 明（i）對 任 意 的Xii∈Gii, Xij∈Gij（1≤i ≠j ≤2）,在 式(2)中，令X =Xii,Y =Xij,Z=Pj，由引理2，有

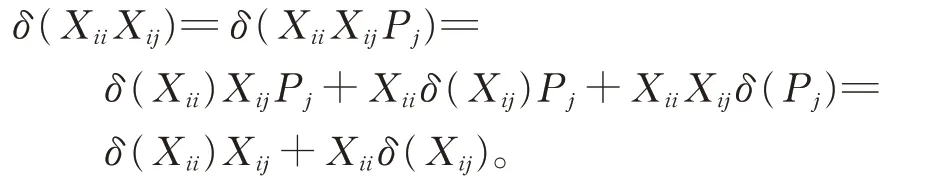
類似地，可以證明（ii）亦成立。

證畢。

引 理4對 任 意 的Xii∈Gii,Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,有

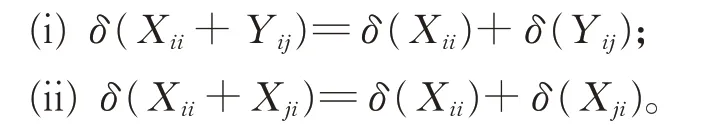
證明（i）對任意的Xii∈Gii,Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,在式(2)中，令

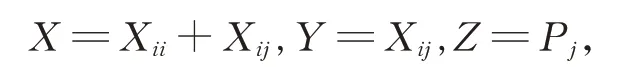
由引理2，有

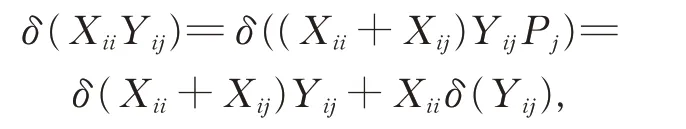
從而由引理3(i)，可得

進而由Gij（1≤i ≠j ≤2）的忠實性，有

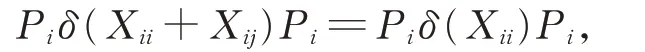
在 式(2)中，令X =Pi，Y =Xii+Xij，Z=Pj（1≤i ≠j ≤2），有

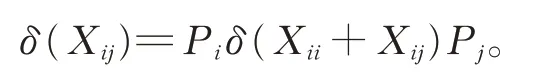
在式(2)中，令X =Xii+Xij，Y =Z=Pj（1≤i ≠j ≤2），有

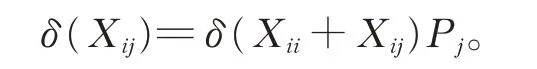
從而由引理2，有

類似地，可以證明Pjδ(Xii+Xij)Pi=0。所以有

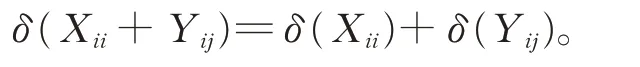
類似地，可以證明（ii）亦成立。

證畢。

引理5對任意的Xii,Yii∈Gii,Xij,Yij∈Gij（1≤i ≠j ≤2）,有

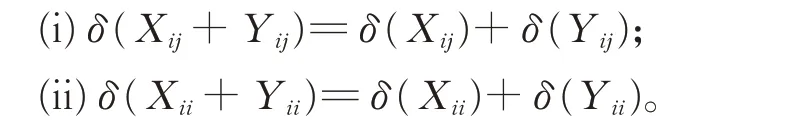
證明(i)對任意的Xij,Yij∈Gij（1≤i ≠j ≤2）,在式(2)中，令X =Pi+Xij,Y =Pj+Yij,Z=Pj,由引理2 和引理4，有

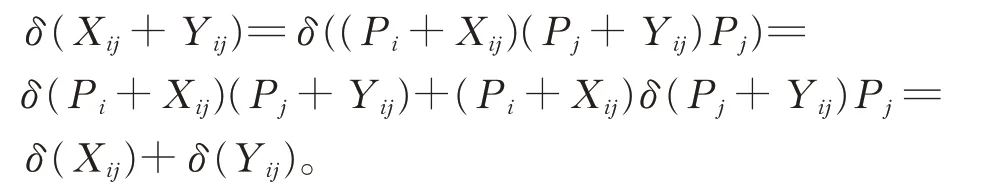
（ii）對 任 意 的 Xii,Yii∈Gii和 Cij∈Gij（1≤i ≠j ≤2）,在 式(2)中，令X =Xii+Yii,Y =Cij,Z=Pj,有

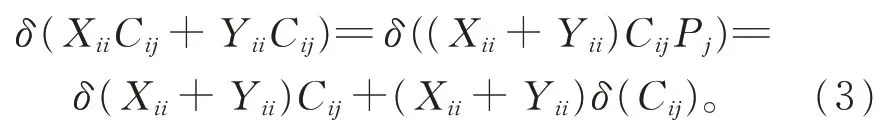
又由引理3(i)和引理5(i)，有

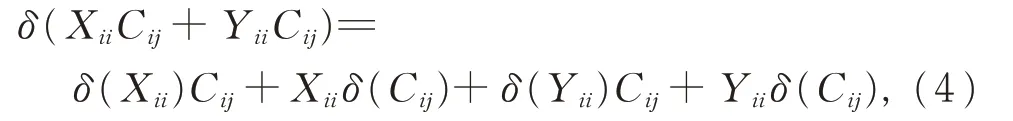
比較式(3)和式(4)，得

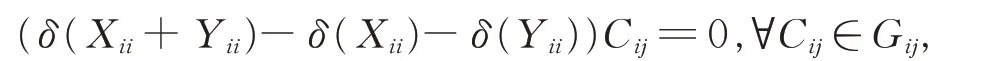
進而由Gij（1≤i ≠j ≤2）的忠實性及引理2，有

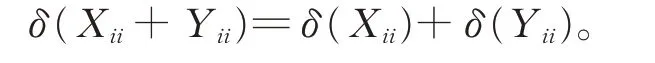
證畢。

引理6對任意的Xij∈Gij（1≤i,j ≤2）,有

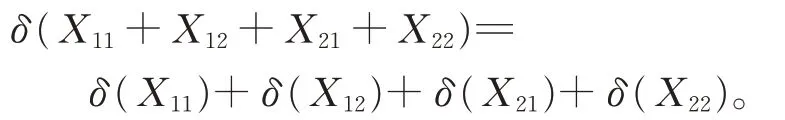
證明對任意的Xij∈Gij(1≤i,j ≤2）,在式（2）中 ， 令 Y =X11+X12+X21+X22, X =P1,Z=P2,有

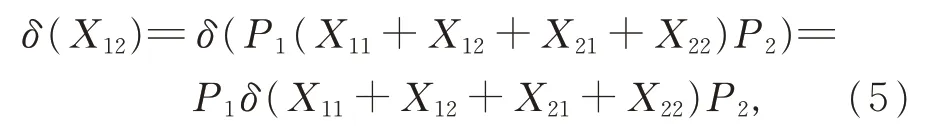
在式（2）中，令Y =X11+X12+X21+X22,X =P2,Z=P1,有

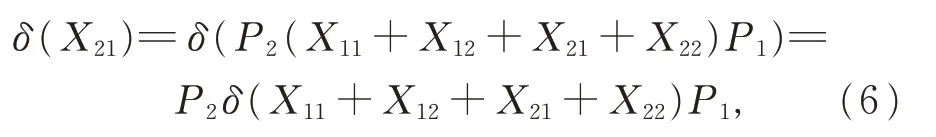
對任意的C12∈G12,在式（2）中，令Y =X11+X12+X21+X22,X =P1,Z=C12,由引理2，有

另一方面，由引理3，有

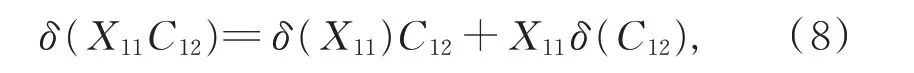
比較式（7）和式（8），得到

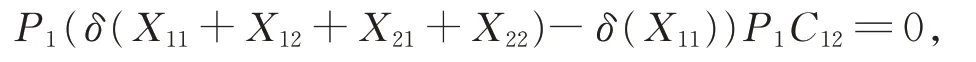
進而由G12的忠實性及引理2，有

類似地，可以得到

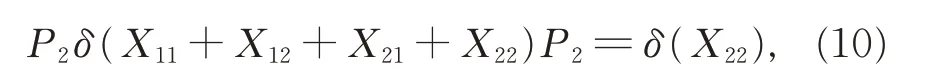
從而由式(5)、(6)、(9)、(10)，有

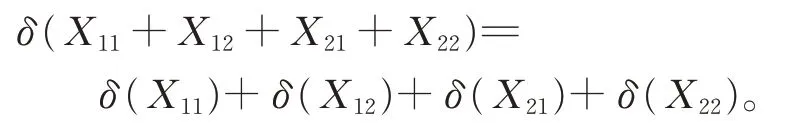
證畢。

引 理 7對 任 意 的 Xii,Yii∈Gii, Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,有

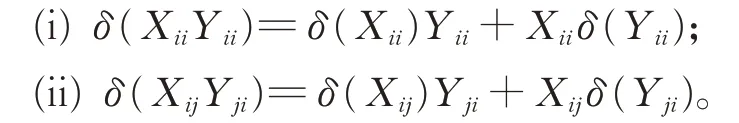
證 明(i)對 任 意 的Xii,Yii∈Gii,Cij∈Gij（1≤i ≠j ≤2）,由引理3，一方面有

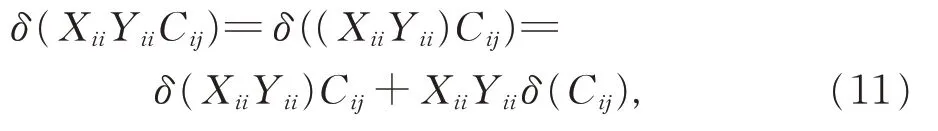
另一方面，有

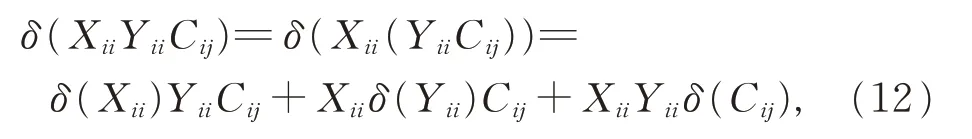
比較式(11)和式(12)，得

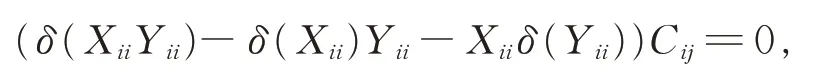
進而由Gij（1≤i ≠j ≤2）的忠實性及引理2，有

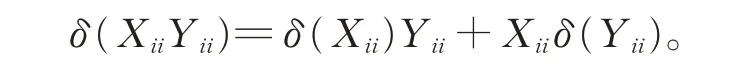
（ii）對 任 意 的Xij∈Gij,Xji∈Gji（i ≠j）,由 于(Xij-XijYji)(Yji+Pi)Pi=0，在 式(2)中,令X =Xij-XijYji,Y =Yji+Pi,Z=Pi，從而由引理2 和引理6，有

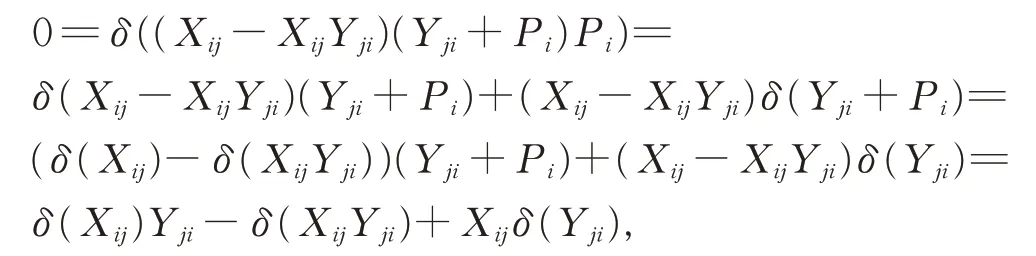
從而有

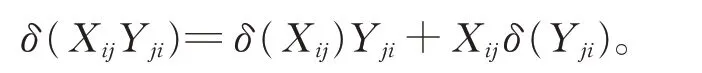
證畢。

定理1 的證明對任意的X,Y,Z ∈G，設

其中，Xij,Yij∈Gij，1≤i,j ≤2，由引理5 和引理6，有

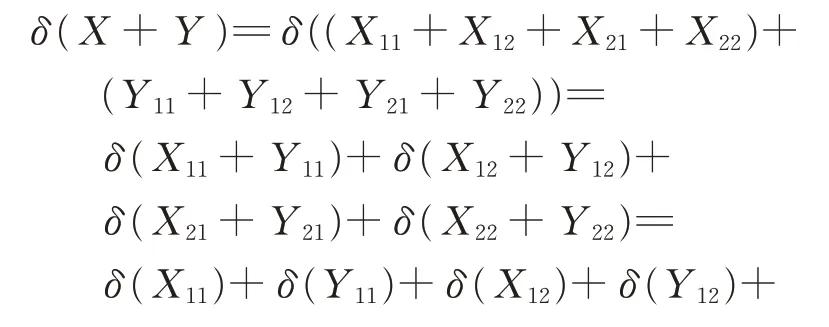
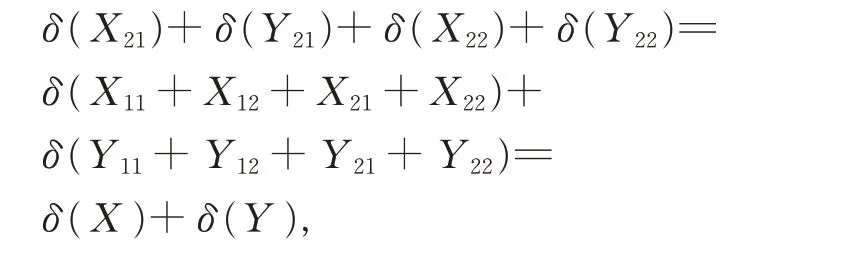
即δ 是G 上的一個可加映射, 從而由δ 的定義知，φ是G 上的一個可加映射。又由引理2、引理3 和引理7, 有

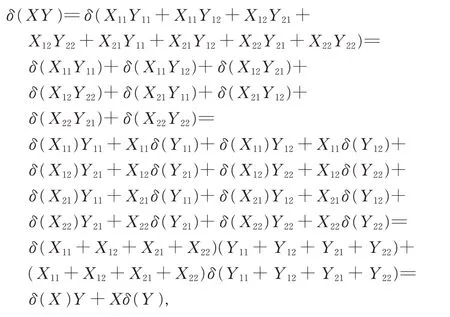
即δ 是一個導子, 所以φ 是廣義矩陣代數G 上的一個導子。

證畢。

作為定理的應用, 有以下推論。

設Α 和Β 是含有單位元的交換環(huán)R 上的代數,若Μ 是忠實(Α,Β)-雙邊模，即Μ 既是忠實左Α 模又是忠實右Β 模, 則稱R-代數

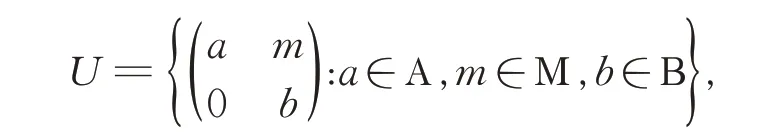
在矩陣通常的加法與乘法運算中是一個三角代數。

推論1設U 是一個2-無撓素三角代數，Ω={T ∈U:T2=0}，且φ 是U 上的一個映射(無可加性假設), 若對任意的X,Y,Z ∈U 且XYZ ∈Ω,有

φ(XYZ )=φ(X )YZ+Xφ(Y )Z+XYφ(Z )，則φ 是一個導子。

推論2設R 是一個有單位元I 且存在非平凡冪等元P 的2-無撓素環(huán)，Ω={r ∈R:r2=0}且φ 是R 上的一個映射(無可加性假設), 若對任意的x,y,z ∈R 且xyz ∈Ω, 有

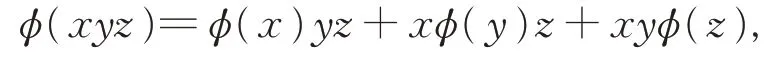
則φ 是一個導子。

證明設Q=I-P，則由于R 是素的，從而PRQ 是忠實的(PRP,PRQ)-雙邊模，所以R 同構于廣義矩陣代數環(huán)：

因此，由定理1 知，φ 是一個導子。

設Χ 是數域C 上的Banach 空間,B(Χ)是Χ 上的全體有界線性算子,A(Χ)是B(Χ) 的一個子代數,F(Χ)是B(Χ)中包含全體有限秩算子的一個理想。若F(Χ)?A(X ),則稱A(Χ)是一個標準算子代數。

設Η 是數域C 上的Hilbert 空間,B(Η)是Η 上的全體有界線性算子,V 是作用在Η 上的一個von Neumann 代數，I 是B(Η)里面的單位算子,Ζ 是V的中心，V′={T ∈B(Η):TB=BT,?B ∈V}是V 的一次換位。若Z=V′∩V=CI, 則稱V 是一個因子von Neumann 代數。

由于標準算子代數和因子von Neumann 代數都是存在非平凡冪等元的素代數，因此，由推論2 ，有

推論3設Χ 是數域C 上的Banach 空間, A(Χ)是Χ 上有單位元的標準算子代數,Ω={T ∈A(Χ):T2=0}，且φ 是A(Χ)上的一個映射(無可加性假設), 若 對 任 意 的 算 子 A,B,C ∈A(Χ) 且ABC ∈Ω, 有

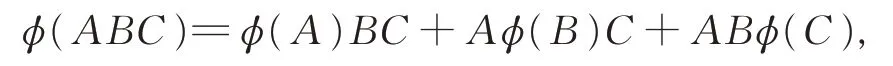
則φ 是一個導子。

推 論4設Η 是 數 域C 上 的Hilbert 空 間, V 是作用在Η 上的一個因子von Neumann 代數，Ω={T ∈V:T2=0}，且φ 是V 上的一個映射(無可加性假設), 若對任意的算子A,B,C ∈V 且ABC ∈Ω, 有

φ(ABC)=φ(A)BC+Aφ(B)C+ABφ(C),則φ 是一個導子。