基于問題解決的科學思維培育策略

趙 瑩

(江蘇省無錫市輔仁高級中學，江蘇 無錫 214123)

1 真實問題與常見問題

目前對問題的定義比較認可的是美國學者厄爾和西蒙所總結的定義,他們認為問題是這樣一種情境:個體想做某件事,但不能馬上知道完成這件事所需采取的一系列行動．[1]無論問題簡單或復雜、抽象或具體、持續的時間長或短,每一個問題都包含3種成分(如圖1所示)．

圖1 問題的3種成分

按照問題的組織程度可以把問題分為結構不良問題(具有不明確的目標、條件和解答,又稱為開放性問題)和結構良好問題(具有明確的目標、條件和解答,又稱為封閉性問題)．真實問題則是指與生產生活實際直接相關聯,往往屬于結構不良問題．例如,“采取哪些措施,可以增加高速行駛汽車在緊急制動情形下的安全性”．單學科和跨學科結構良好的問題常被合稱為常規問題,它也是學生在學習過程中最常遇到的問題．例如,“一輛以30 m/s勻速行駛的汽車,以2 m/s2加速度剎車,車能運動多遠”．本文主要探討,如何在解決真實問題和常規問題的過程中,提升學生的模型建構、科學推理、科學論證、質疑創新等科學思維能力．

結構不良問題的解決可分為7個階段(如圖2所示),結構良好問題的解決可分為4個階段(如圖3所示)．[1]

圖2 結構不良問題的解決步驟

圖3 結構良好問題的解決步驟

2 借助問題解決提升學生科學思維能力的策略

2.1 借助真實問題解決,提升學生科學思維能力

2.1.1 借助真實問題解決,提升學生科學思維能力的案例

下面是筆者在課堂上的一個教學案例．原文為近500字的新聞報道,限于篇幅,筆者已剔除案例中部分與物理無關的信息．因為剔除信息的過程就是信息進行甄別、提取、局部表征的過程,而這些都是整體表征問題的前提,所以老師在實際課堂呈現給學生的應是案例的全文．

例1. ……發生一起惡性交通事故．一輛卡車急剎車,車上的水泥管卻因慣性沖破擋板壓扁了車頭,司機被壓在駕駛室中,當場斃命……據目擊者介紹……車速并不快,行至滬閔公園門口的斑馬線時,有幾個行人從馬路對面走來,卡車為避讓而緊急剎車……大卡車上滿載著6根長達十幾米的水泥管子,卻沒有任何捆綁措施．其中的兩根管子向前移動了近一米,整個車頭已被完全壓扁……為避免事故發生,請給駕駛員一個合理化的建議．

圖4 真實問題解決實例

這是一個典型的真實問題,其結果有一定的開放性,筆者按照圖4所示思路引導學生．學生經過一段時間的問題表征(局部、整體)、科學推理、科學論證后,形成了不少論證結論,典型的結論可小結為:降低車速,避免緊急剎車;將水泥管捆扎牢,增大水泥管與駕駛室間的距離;提高駕駛室后側擋板的強度;注意觀察路上情況,及時發現險情;生命至上的安全意識．學生還有很多創意,比如設計防滑墊、為駕駛室后側擋板增加防撞緩沖裝置、開發報警系統等等,這些都體現了他們一定的創新能力潛質．

2.1.2 借助真實問題解決,培育科學思維能力的范式

每一個真實問題解決的過程幾乎都包含了模型建構、科學推理、科學論證、質疑創新等科學思維的各個方面．怎樣借助真實問題的解決,更有效的培育學生的科學思維,筆者概括出了一個教學的范式(如圖5所示)．這只是范式,并非一個嚴格的固定模式．

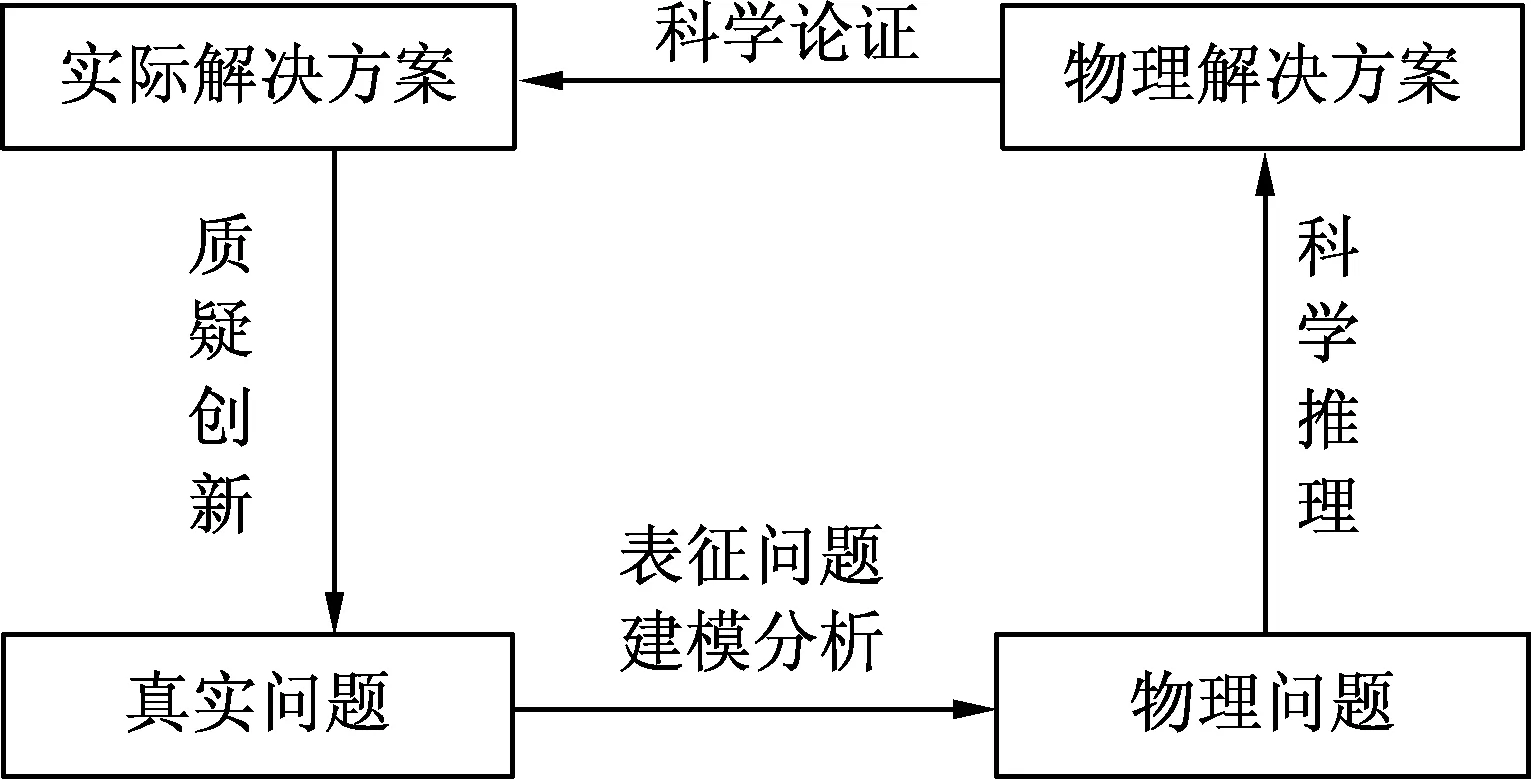
圖5 借助真實問題培育科學思維能力的范式

2.2 借助常規問題解決培育科學思維的幾點建議

常規問題是教學中最常見的問題,其在培育科學思維能力方面的作用不言而喻．關于此類的研究和文獻也不少,筆者在此不再全面展開,僅提幾點建議,供參考．

2.2.1 問題呈現適度“情境化”,提高學生表征問題的能力

學生今后的學習與生活中將會面對很多前所未有的、復雜的、不確定的問題場景,創造力是21世紀的必備品格．近年的高考考題與生產、生活緊密聯系的趨勢非常明顯,考題也經常以情境化的方式呈現．情景化的問題里面蘊含著大量潛在的信息,什么有用,什么沒用,都是不明確的,學生能夠進行甄別,并把它提煉出來、組織起來,也是素養的表現．問題的答案可以存在一定的開放性,長期封閉性問題的練習,易使學生的思維形成一定的局限性,會影響對他們質疑創新能力的培養．

2.2.2 循序漸進建構模型,鋪設解決問題的底層支架

模型建構是根據研究問題和情境,在對客觀事物進行抽象和概括的基礎上,構建易于研究的、能反映事物本質特征和共同屬性的理想模型、理想過程、理想實驗和物理概念的過程．在面對問題時,學生要能從復雜的情境中正確的表征問題,學會用聯系的眼光看待事物,學會正確歸因,選用合適的物理模型解決問題．建構模型有助于學生學會抓住事物的關鍵要素,加深他們對概念、過程和系統的理解,形成系統思維．

例2.斜面—滑塊模型是高中物理中最常見的模型之一．通過此類問題的解決,可以提高學生靈活應用隔離法、整體法解決問題的能力．圖6甲所示,當斜面靜止時,滑塊分別處于:靜止→勻速下滑→勻加速下滑等三種狀態,討論斜面和地面之間的摩擦力問題．在此基礎上,再討論圖6乙所示,當小球與車廂相對靜止時,按照斜面光滑和不光滑兩種情況,分別討論繩子與豎直方向夾角α和斜面傾角θ之間的關系．解析從略．

學生在解決新場景問題時,總會自覺或不自覺的應用已有的認知去表征問題、歸類問題、尋找解決問題的圖式,而模型建構教學則為此做好了最基礎的思維準備．模型是轉變、遷移的前提,是萬變不離其宗的思維錨點,教師應該為轉變而教、為遷移而教．經過梳理,筆者列出高中物理關于模型建構教學的部分實例,供參考．

2.2.3 借助函數思維的培育,提高學生科學論證的能力

以函數思維來審視物理中變量之間的關系,往往能夠化難為易、化繁為簡,起到事半功倍的作用,不但能提高學生的知識遷移能力,而且可以開闊學生的視野,加強學生對物理學習的深度,激發學生的興趣．若在函數思維培養過程中常用一些函數術語進行教學,對教學過程進行的“顯性化”處理,則學生遇到類似問題應用函數思維的“敏感度”會提高．常用的術語如:“自變量”、“應變量”、“表達式”、“定義域”、“值域”、“分段函數”及“函數的單調性”等．[3]

例3.人造衛星繞地球做勻速圓周運動,其軌道半徑為r,線速度為v,周期為T,要使衛星的周期變為2T,可以采取的辦法是

(B)v不變,使軌道半徑變為2r.

(C) 使衛星的高度增加r.

答案選(D),詳解從略．解決該問題的關鍵是,關系式中分子上的物理量與分母上的物理量是獨立量(一個物理量的變化不會引起其他量的連鎖反應),還是關聯量(與獨立量相對)．在說一個物理量(應變量)與其他物理量(自變量)間是什么關系時,要保證一個自變量變化時,其他自變量能保持不變,即符合控制變量法的要求．由于知識水平和看問題的角度所限,學生容易犯上述錯誤,教師在教學中時常指導學生檢驗表達式中各自變量的獨立性．

2.2.4 指導學生學會估算,提高學生科學推理的能力

圖7

在討論定量問題時,未必所有問題都是越精確越好,有時是沒有必要,有時是不可能,也有時是既沒必要也不可能．在研究某些問題時,甚至我們只要知道數量級即可以,如用油膜法估測分子的大小,應用萬有引力定律估算天體間的距離等．矛盾論的哲學原理告訴我們,只有忽略次要矛盾,突出主要矛盾,抓住矛盾的主要方面,才能利于對問題的整體把握．

例4.一個小石子從離地某一高度處由靜止自由落下,某攝影愛好者恰好拍到了它下落的一段軌跡AB.該愛好者用直尺量出軌跡的長度,如圖7所示.已知曝光時間為10-3s,則小石子出發點離A點約為

(A) 6.5 m. (B) 10 m.

(C) 20 m. (D) 45 m.

雖然絕大部分學生選擇了正確答案(C),但筆者在講評的過程中,仍組織學生對這個問題進行了深入的探討．首先,筆者在黑板上呈現了學生中幾種常見的解法(略),其共同缺點是步驟較繁、運算量大;然后,筆者直接用AB段的平均速度代替A的速度,去求OA的間距;最后,筆者再問學生這種解法“靠譜”嗎?不少學生第一感覺這樣的做法有“瑕疵”,但就結果而言,好像還是可以接受的．[4]

2.2.5 借助物理學史中重大的“破與立”實例,培育學生質疑創新的精神

物理學不少規律的發現都經歷了漫長而曲折的過程．通過此類問題的討論,可以幫助學生豎立敢于質疑、勇于創新、不迷信權威的科學精神．

例5.人類在天體運動規律方面的認識,經歷了“地心說→日心說→第谷的天文觀測→開普勒三定律→萬有引力定律”等階段,其中布魯諾為了日心說甚至付出了生命的代價;人類對電與磁關系的認識,經歷了“電和磁各自獨立發展階段→奧斯特對電流磁效應的研究→安培對安培力的研究→法拉第發現電磁感應現象→麥克斯韋方程組的建立”等階段;人們關于光的本性認識,經歷了“光的粒子說→光的波動說→粒子說與波動說的爭論階段→光子說→光的波粒二象性”等階段,其過程也是一波三折．[5]

3 結語

學生是社會主義事業的建設者和接班人,今后會面對各式各樣的“問題”,而科學思維則是順利解決這些“問題”的核心素養之一,其中的質疑創新精神對民族復興更是至關重要,值得大家共同努力!