耦合相振子系統同步的序參量理論*

鄭志剛 翟云 王學彬 陳宏斌 徐燦?

1)(華僑大學系統科學研究所,廈門 361021)

2)(華僑大學信息科學與工程學院,廈門 361021)

3)(北京郵電大學理學院,北京 100876)

節律行為,即系統行為呈現隨時間的周期變化,在我們的周圍隨處可見.不同節律之間可以通過相互影響、相互作用產生自組織,其中同步是最典型、最直接的有序行為,它也是非線性波、斑圖、集群行為等的物理內在機制.不同的節律可以用具有不同頻率的振子(極限環)來刻畫,它們之間的同步可以用耦合極限環系統的動力學來加以研究.微觀動力學表明,隨著耦合強度增強,振子同步伴隨著動力學狀態空間降維到一個低維子空間,該空間由序參量來描述.序參量的涌現及其所描述的宏觀動力學行為可借助于協同學與流形理論等降維思想來進行.本文從統計物理學的角度討論了耦合振子系統序參量涌現的幾種降維方案,并對它們進行了對比分析.序參量理論可有效應用于耦合振子系統的同步自組織與相變現象的分析,通過進一步研究序參量的動力學及其分岔行為,可以對復雜系統的涌現動力學有更為深刻的理解.

1 引 言

節律,即系統呈現的隨時間周期變化,廣泛存在于我們生活的世界,從鐘擺、星體運動到生物鐘,都是不同系統典型的動力學行為.復雜與非線性系統會表現出多種多樣的自組織與群體性行為[1-3],而不同的節律之間也可以通過相互作用涌現出各種集體的自組織現象,其中同步是最典型、最直接的有序行為,它也是諸如非線性波、時空斑圖乃至各種生物集群行為(例如鳥群、魚群、蜂群、蟻群、人類社會等)的內在物理機制[4,5].

作為一種最基本的協同現象,同步研究可以追溯到1673年Huygens發現的關于兩個相鄰鐘擺同步的討論.在后來的很多不同物理問題中,人們都發現了同步現象.電子與無線電工程的發展很大程度上促進了關于同步的研究.相比于現象觀察及實驗研究,同步的理論研究相對要滯后得多,直到20世紀初關于極限環的研究才得到了突破.極限環是非線性耗散系統的一類典型時間振蕩解和吸引子,不同時間振蕩之間可以通過相互作用產生新的協同.由于大量看似不同的系統都具有可以用極限環描述的時間振蕩,人們逐漸認識到,在各種不同同步行為的背后應該具有共同的物理機理[5].Wiener[6]在其專著中關于“腦電波與自組織系統”一章指出,腦電波的出現是來自于不同頻率的鎖定(pulling together of frequencies),而且這種行為與其他諸如螢火蟲同步閃光、蟋蟀同聲鳴唱等現象有著共同的機制.而如何在極限環基礎上來研究驅動或相互作用的振子間的同步在理論上就成為重要課題.

Winfree[7]于1967年提出了全局耦合振子模型.他認識到,在同步問題上,極限環之間相互作用起作用的關鍵自由度是其相位,因此只需要考慮耦合的相位振子模型即可揭示同步的動力學實質.Winfree模型的動力學方程可寫為

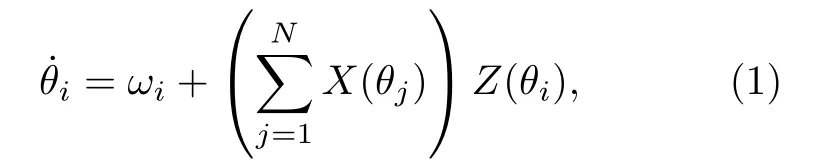
這里用 i =1,2,··,N 來標記不同振子,{θi}代表振子的相位,{ωi}為振子的自然頻率,它們各不相同,設符合某個統計分布函數g(ω).Winfree發現,自然頻率分布較窄時振子之間會相互同步[7].這樣,在眾多不同物理背景下出現于不同體系中的很多現象就都可以利用耦合相振子系統的同步動力學來得到非常好的解釋.大量相互作用振子出現的整體同步行為是一種典型的集體涌現,如何解析刻畫同步涌現是一個挑戰性課題.

Kuramoto[8-10]考慮振子數目 N → ∞(熱力學極限),自然頻率 { ωi} 為單峰分布g(ω),振子間相互作用是耦合強度為K的全局性平均場形式,并取最簡單的相位差的正弦函數sin(Δθ)來描述相互作用.平均場耦合相振子模型可寫為

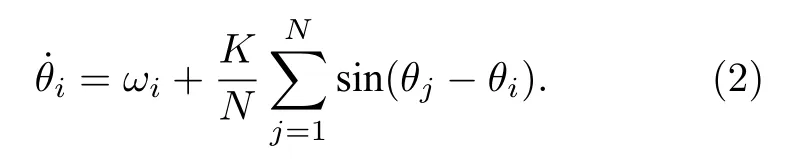
該模型被后來研究者稱為Kuramoto模型[11].我們還引入振子的集體自然頻率一般情況下自然頻率分布函數設為關于的對稱分布.為討論方便,通常設分布對稱性滿足

盡管振子的自然頻率各不相同,有相互作用時(K≠0)各振子的實際振動頻率都會相應地從K=0時的自然頻率{ωi}處發生偏離,并隨耦合強度變化而變化.可定義振子的平均頻率Ωi為

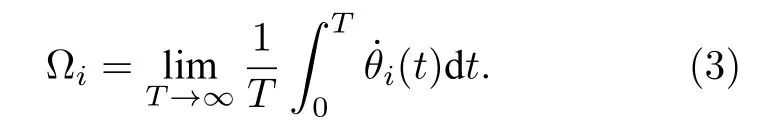
為描述振子的整體同步情況(相干程度),Kuramoto引入如下的序參量,將其定義為所有振子相位復函數的平均場:

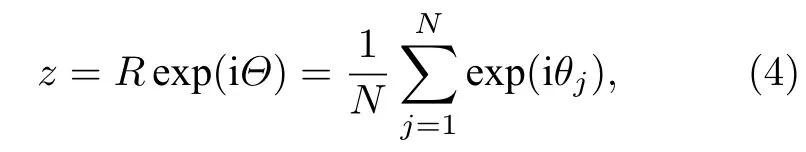
其中復序參量的模R=|z|描述振子的相干性強弱,Θ為一任意相位.

在耦合強度很弱時,只有自然頻率極其靠近的振子才會同步,但它們所占的比例幾乎可以忽略,大量振子的Ωi都不等,它們在任一時刻的相位都均勻分布于0— 2π之間,如圖1(a)所示,此時R=0.隨著耦合強度的增加,越來越多的振子會同步,平均頻率Ωi相等,這些同步的振子相位之間會靠近并保持固定相位關系,振子不再均勻分布,如圖1(b)所示.當所有Ωi都相等時,R就不為零,表明此時振子之間可保持固定的相位關系.存在一個臨界的耦合強度 Kc,當 K ≤ Kc時 R=0;當 K ≥ Kc時,R≠0.在很強的耦合下,振子相位會靠得很近,形成整體的同步大集團,如圖1(c)所示.大量耦合振子可以通過相互作用克服自然頻率不同帶來的無序而涌現出同步態實質上就是一種典型的非平衡相變.在臨界Kc處發生的相變在理論上可以處理.Kuramoto利用統計物理學方法和自洽方程成功求解[9,10],理論上得到了臨界耦合強度Kc,并得到在Kc附近序參量R的臨界行為.

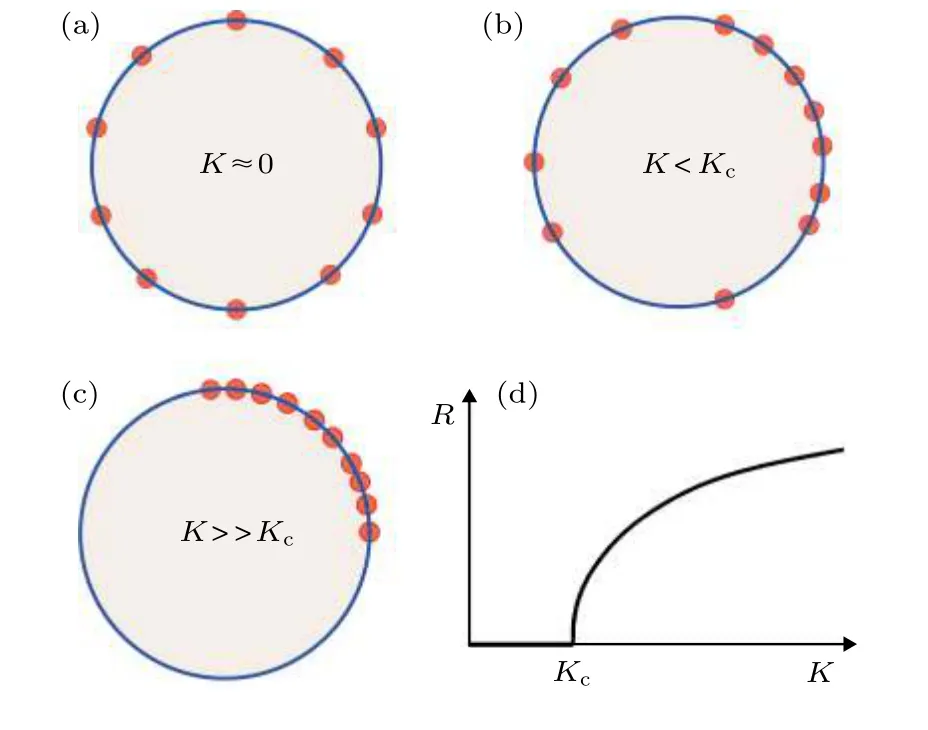
圖1 耦合振子同步示意圖(a)在耦合強度-很弱時,大量振子不同步,任一時刻相位均勻分布于02π之間;(b)隨著耦合強度的增加,越來越多的振子會同步,振子不再均勻分布;(c)在很強的耦合下,振子相位會靠得很近,形成整體的同步大集團;(d)序參量隨耦合強度的變化Fig.1.A schematic diagram of synchronization of coupled oscillators:(a)Most of the oscillators are asynchronous and evenly distributed along the circle;(b)with increasing the coupling,more and more oscillators are synchronized and are no longer evenly distributed;(c)under a strong coupling,oscillators form a single synchronous cluster,and the phases of oscillators are close to each other;(d)dependence of the order parameter on the coupling strength.

結合具體的物理背景,Kuramoto模型的應用范圍和領域大大拓展[11-17].人們研究了不同耦合函數[18,19]、不同耦合網絡拓撲結構[14,15,20-25]、脈沖耦合[26]等情況下的同步,探討了同步涌現的玻璃態[27]、非對稱耦合及其行波和駐波波態[28,29]、慣性效應[30,31]、阻挫效應[32-35]、時間延遲效應[36]、外場驅動效應[37]、時變耦合[38]等與實際物理背景密切相關的問題.以Kuramoto模型為代表的耦合振子系統集體動力學問題時至今日一直是重要的研究熱點.

對于大量振子同步的研究有幾種不同層次和方法.利用非線性動力學[39-41]和同步分岔樹方法[42-44]可以對耦合振子的微觀動力學進行研究.當振子數目 N ?1 時,微觀動力學分析會變得很繁雜,可以利用統計物理和宏觀方法開展研究.早期Kuramoto基于統計物理學方法和自洽方程理論成功地對同步相變進行了解析研究[9].但自洽方程方法建立在同步態為定態的前提下,近年來人們發現了大量非定態集體動力學行為,因此有必要建立一套反映集體動態行為的統計與宏觀理論[45].20世紀90年代初,Watanabe與Strogatz發現[46],一類具有對稱性的耦合振子系統的高維動力學可以通過引入M?bius變換(后稱為Watanabe-Strogatz變換,簡稱WS變換)精確降維到三維空間,這意味著系統的部分可積性.Ott與Antonsen[47,48]提出了序參量擬設理論,將高維微觀動力學研究降維到二維序參量空間加以研究.人們隨后意識到,OA擬設下的二維動力學實際上是WS變換下的三維動力學的進一步降維[49,50].

耦合振子系統同步的序參量動力學研究大致包括如下幾個重要和基礎問題.第一,序參量是表征整體行為的特征量,那么對于大自由度的耦合振子系統,序參量是如何涌現的？第二,序參量及其涌現的物理意義是什么？第三,如何用序參量刻畫不同的同步或有序狀態及其轉變？第四,如果有不止一個序參量共存,這些序參量之間如何競爭？第五,對于實際系統,如何引入恰當的表征集體行為的序參量來刻畫有序行為？如何從復雜系統的動態大數據中重構序參量動力學？本文將集中于上述的前三個基本問題,對大量振子組成的系統產生同步作為一種典型的涌現行為開展宏觀和統計層面的研究,總結、回顧并對比幾種不同的序參量理論框架[51].

2 Kuramoto自洽方程理論

首先來看Kuramoto如何通過引入序參量并利用求解自洽方程來解析處理同步問題.自洽方法的基礎是通過假設系統存在一個不隨時間改變的定態,在此狀態下序參量為一個待定的定值,通過序參量的定義和系統定態的運動方程,得到待定的序參量的值,并在分析的過程中得到此序參量與相應定態的存在條件.自洽方法從其方法本身便限定了其適用范圍,雖然只能用于對定態的分析,卻可以不受具體動力學的限制,是振子系統分析中廣泛使用的方法之一.

首先,假定振子數N足夠多情況下,序參量(4)式與N無關且不隨時間變化.考慮到Kuramoto模型(2)式相互作用的平均場形式,很容易可以將方程(2)重新寫為

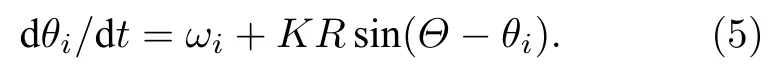
如果能定出R,則方程(5)完全可以求解,但這不是一件簡單的事.一個可行的辦法是帶著未知R繼續討論,建立一個關于R的方程來將其求解.該方程即為自洽方程(self-consistent equation)[8,51].下面的討論即是圍繞這一主題展開.

顯然R=0對應于無相互作用的情形(均勻分布解),這個非相干態總是系統的一個解,但不總是穩定.當 K ＞Kc時均勻分布解失穩.另外一個解是Ωi都相等時的解,此時振子之間可以保持固定的相位,R≠0,所有振子都以集體頻率轉動,此解在 K ≤Kc時不穩定.只要有 Ωi不相等,θi就總是均勻分布于0—2π 之間.

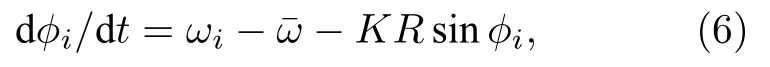
此方程正是過阻尼情形下的單擺方程.它有兩個解.1)同步解.當方程(6)描述的第i個振子滿足時,該振子的相位φ就會保持定值這意味著所有滿足該條件的振子都會以頻率運動,它們處于同步狀態.2)非同步解.當方程(6)描述的振子 i滿足時,則該振子的相位φ就會隨時間變化,且凡是自然頻率滿足該條件的振子都處于非同步狀態.

振子數N→∞時,φi在0—2π之間會形成分布.設分布函數為 P(φ,ω,t),它不僅依賴于 φ,還依賴于振子自然頻率ω.平均場由分布函數可表為

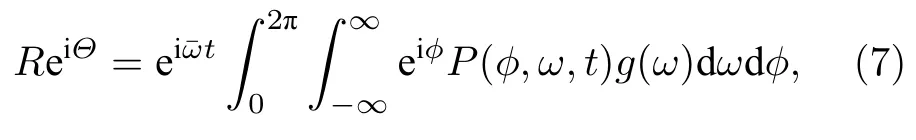
單振子分布函數滿足連續性方程:

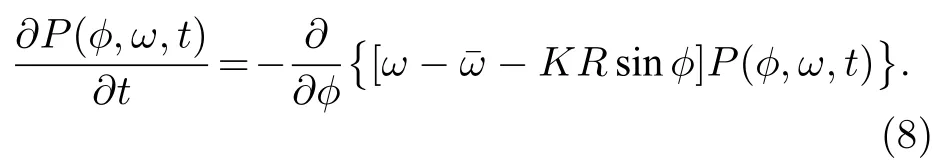
考慮到振子具有自然頻率分布,如果只考察φ的統計分布,則需要進一步對頻率做積分P(φ,t)=這些振子相位的分布直接決定了相關的平均量,例如序參量,因而很重要的一點就是如何確定分布函數.根據上面討論的兩類定態解,可把分布P(φ)分解為同步與非同步兩部分:

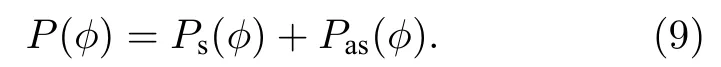
同步振子的相位φ趨于不動點,與時間無關,因此Ps(φ)可由自然頻率分布得到:

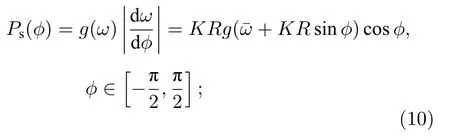
非同步振子的相位φi則隨時間變化,因為φi隨時間變化是非均勻的,單位時間內探測到φ在φ→φ + dφ之間的概率反比于相速度 |把運動方程(6)式代入并歸一化可得到

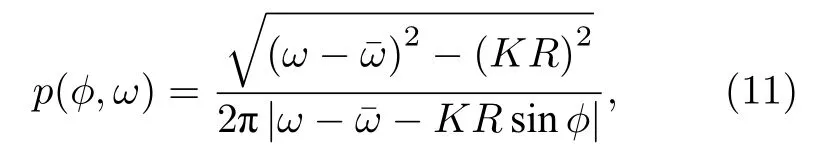
因此

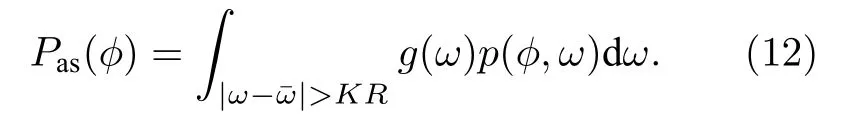
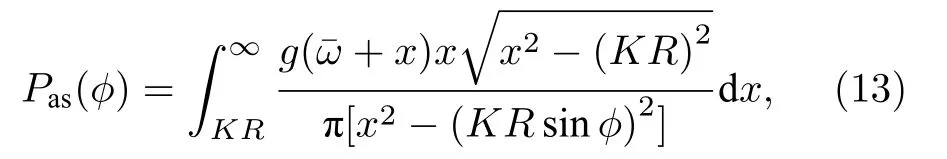
將前面引入的平均場用分布寫出來,并利用(9)式可得

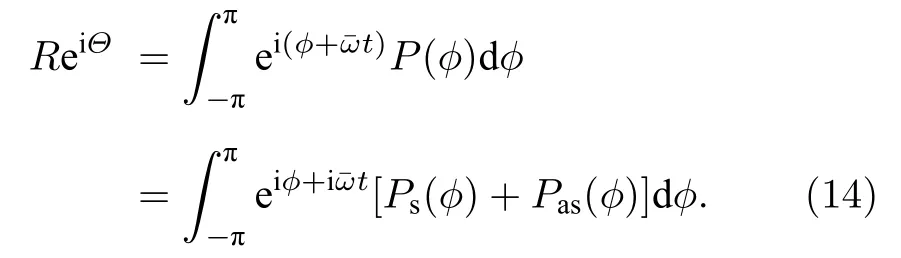
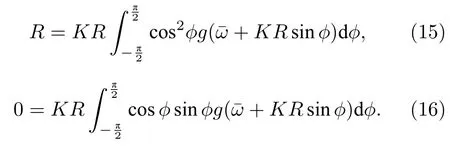
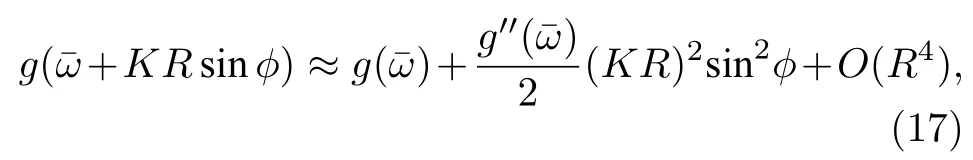
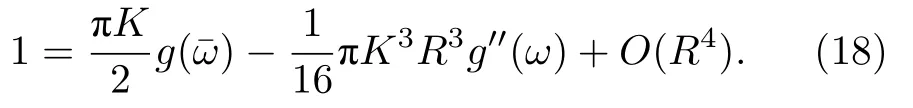
當 K →Kc時,由于R2項為高階小量,R→0,由此得到同步臨界耦合強度為

將(19)式代回(18)式可以確定在臨界點Kc附近R的行為:

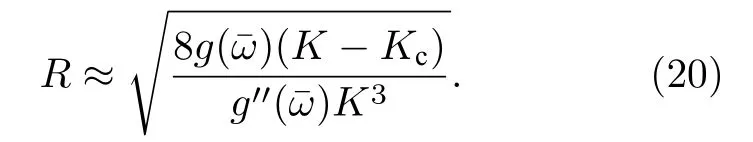
3 序參量及其涌現的自組織原理

耦合振子同步微觀動力學的研究表明,大量耦合振子隨著耦合強度的增加會經歷由部分同步到整體同步的過渡,相空間維數隨同步進程而逐漸降低,整體同步時,系統在相空間的復雜運動會落到一個極低維的空間[42-44].降維意味著系統發生同步的時候,只需要少數變量即可刻畫耦合振子系統的同步.該結果為多振子體系同步的宏觀及序參量描述提供了事實基礎.

統計物理學建立了從微觀到宏觀之間的聯系,進一步通過統計定律來計算微觀量的統計平均來得到宏觀熱力學量[27].熱力學和統計物理學的思想和方法為處理耦合振子同步轉變問題提供了思路.由大量相互作用振子組成的系統通常是非平衡系統,同步是大量振子整體動力學從無序向有序的非平衡相變.非平衡行為研究自20世紀中期發展起來的以耗散結構理論[52,53]、協同學[54,55]以及多學科分支形成的自組織理論等為描述眾多的非平衡相變現象的共同本質提供了重要依據.

耗散結構理論認為,處于非平衡狀態的系統會在一定范圍內維持原有熱力學狀態,一直到遠離平衡到一定臨界值,熱力學分支失穩使系統進入到有序的結構分支.非平衡相變現象在自然界各個領域有形形色色的表現,物理表現十分不同,而內含的數學實質是有明顯的規律,由此形成了以反映擴散方程等為核心的刻畫宏觀自組織過程的耗散結構理論[53].

Haken的協同學則關注于由大量自由度構成的復雜系統在外參量的驅動下和在子系統之間的相互作用下如何以自組織的方式在宏觀尺度上形成空間、時間或功能有序結構的條件、特點及其演化規律[54].協同學的基本原理是支配原理(slaving principle),它認為,協同系統的狀態由一組狀態參量來描述,這些狀態參量弛豫時間尺度是不相同的,慢變的線性不穩定模稱為慢變量(slow variable),而快變的線性穩定模稱為快變量(fast variable).當系統接近于發生顯著質變的臨界點時,慢模數目會減少為只有一個或少數幾個,這些慢變量可以完全確定系統的宏觀行為并表征系統的有序化程度,故而稱為序參量.而為數眾多的快模則由慢模/序參量所支配,并可將其絕熱消去,由此可以建立少自由度的協同學基本方程.在序參量方程基礎上,我們就可來研究協同系統的各種非平衡定態/非定態、穩定性及其非平衡相變[55].

支配原理在數學上即絕熱消去,即可以對快速變化的變量進行平均加以消去,只保留變化慢(絕熱)的變量.該方法在物理上有著深刻含義.下面以如下的n維動力學系統為例來簡單介紹一下支配原理:

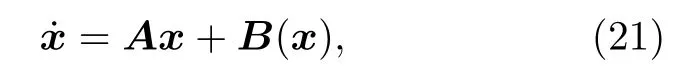
其中x(t)=(x1(t),x2(t),···,xn(t))T為n維狀態矢量,A為 n ×n 常數矩陣,B(x)包含x的二次以上代數式矢量.設x=0為方程的解.設矩陣A的本征值為 { λi,i=1,2,···,n},其中本征值按照其實部由大到小排列.如果所有本征值實部均為負,即 { Reλi＜ 0,i=1,2,···,n},那么x=0為穩定解.改變參數使A的m個模失穩,而其他模仍然保持穩定,即假設該模對應的本征值且通過引入一個T矩陣進行如下的線性變換

將A對角化

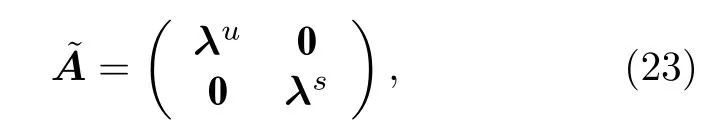
這里 λu,s分別為 m × m與(n — m)×(n — m)對角子矩陣.則(21)式可改寫為

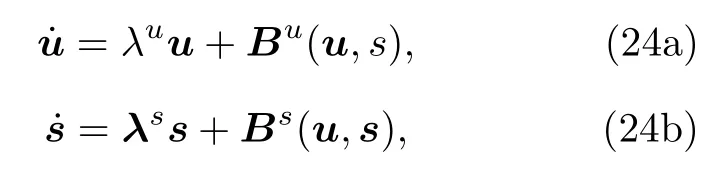
這里x(t)=(u(t),s(t))T,其中u(t)=(u1(t),u2(t),··,um(t))T,s(t)=(s1(t),s2(t),··,sn-m(t))T,s(t)為滿足(24b)式的快變量,而 u(t)為滿足(24a)式的慢變量.按照支配原理絕熱消去,令(24b)式左邊=0,由此n — 1個方程可將n - m維矢量s作為u的函數解出,并代入(24a)式可得到m維的非線性方程

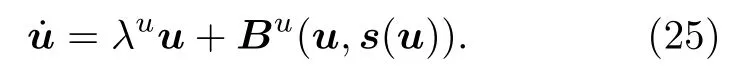
一般實際問題中首先失穩的模往往很少,常常是一兩個,從(24)式到(25)式,在理論上可以看作是從多變量方程到少數序參量方程的約化,在動力學上也產生了極大簡化,這是支配原則在討論相變點附近行為時給出的有益結果.

需要注意的是,變量的快慢不能理解為其他諸如振蕩的快慢,而是弛豫的快慢,因此嚴格來說應該稱為快/慢弛豫變量.慢變模式有時可能本身就是高頻振蕩,該模對于擾動響應的弛豫時間長短才是判斷該模為快或慢的標準.

序參量有著幾何上的意義,支配原理也密切聯系著中心流形定理.中心流形定理是一種常用的幾何降維方法,它利用流形與對應子空間相切的特性,求出系統在中心流形上的約化方程.對于高維動力系統來說,通過傳統的分岔行為很難直接研究其動力系統.為了更好地抓住所要研究問題的本質,一般采取中心流形定理等降維措施將其化為低維方程再進行研究.

4 序參量動力學理論

下面將從耦合振子微觀動力學方程出發,利用統計力學方法建立分布函數方程,并通過統計平均引入各階序參量,建立相應的序參量方程,并進一步討論對方程的降維.

4.1 廣義序參量

從一般形式的全局耦合振子系統運動方程出發:

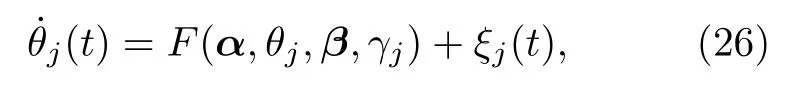
其中 j=1,2,··,N,ξj(t)為作用于第 j個振子上的隨機噪聲,設為振子間無關聯的高斯白噪聲,滿為一組均勻控制參量,這些參量對所有振子均相同,如通常考慮振子間相互作用強度相同.γ ={γ1,γ2,···,γN} 為一組非均勻控制參量,它們對不同振子不一樣.例如振子的自然頻率通常各不相同,此時{γi=ωi}.

定義一組廣義序參量α={αn},其分量為如下的n階序參量:

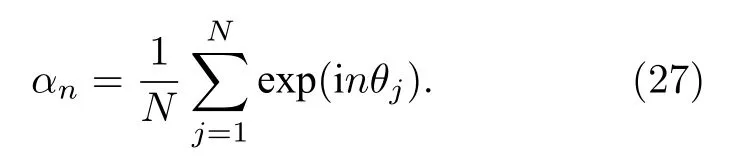
當n=1時,α1即是Kuramoto引入的相干因子.n ＞ 1時 αn為高階序參量[56].在熱力學極限N→∞下,可以引入振子相位的密度分布函數ρ(γ,θ,t),ρ(γ,θ,t)dθ為一個振子在時刻 t相位處于θ→θ + dθ的概率或時刻t相位處于θ→θ + dθ內的振子數密度.它滿足(12)式對應的Fokker-Planck方程:

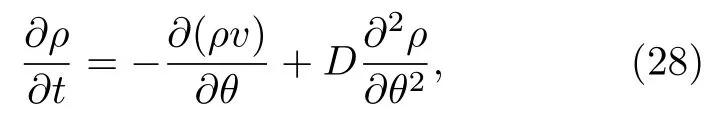
其中速度場 v=F(α,θ,β,γ).在沒有外加噪聲(D=0)時,分布函數方程退化為如下的連續性方程

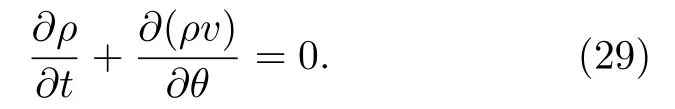
在一般情況下振子是非全同的,即分布函數ρ(γ,θ,t)與γ有關,系統總的分布函數需要對所有非均勻參量求和,例如,如果 { γi=ωi},則分布函數為

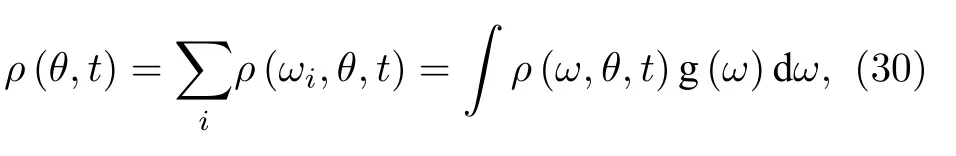
其中 g(ω)為自然頻率分布.ρ(θ,t)包含了振子系統集體行為的所有信息.在同步問題宏觀層面,我們最為關注序參量α={αn}.對于均勻系統即沒有非均勻參量γ,利用分布函數,序參量可表為如下積分:

如果系統有非均勻性,則需要同時對非均勻參量γ求和.例如,如果非均勻參量是振子自然頻率,則有

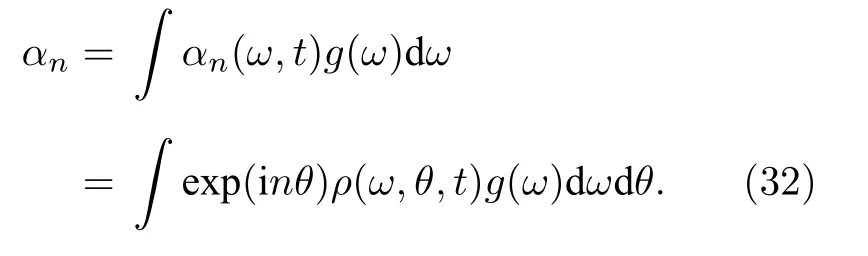
可以看到,n階序參量αn實際上就是exp(inθ)的統計平均,或稱為exp(iθ)的n階矩.由于宏觀量的各階矩描述與分布函數描述等價,可由一方信息推知另外一方的信息.還可以看到,廣義序參量實際上就是分布函數ρ(θ,t)的傅里葉變換系數.

4.2 Ott-Antonsen擬設

下面先考慮全同振子系統的序參量運動方程.利用序參量的定義(27)式,對其進行時間求導,并利用振子運動方程(26)式可以得到

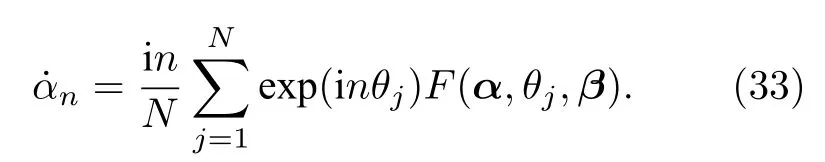
由于函數 F(α,θ,β)是循環變量相位 θ 的 2π 周期函數,因此可做傅里葉展開:

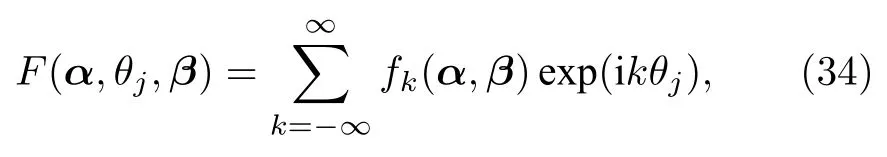
將展開式代入運動方程(33)中可得序參量運動方程為

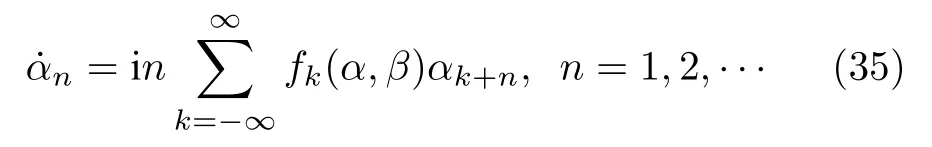
考慮最簡單的耦合形式,即(34)式的傅里葉分解中只需包含最低階項:

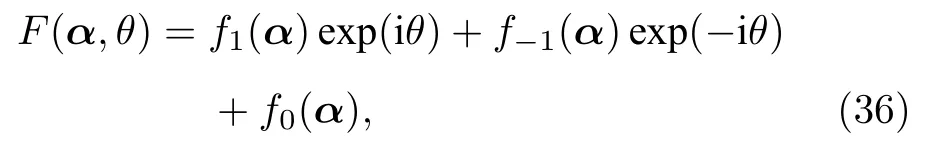
則序參量運動方程(35)簡化為

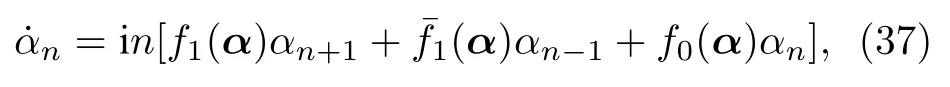
廣義序參量可看成是相位振子的集體坐標變量,這意味著相位運動方程(26)通過上述變換可以化為運動方程(35)和(37),它們都是一組耦合的序參量方程,處理該序參量方程組的難度等價于相位運動方程(26),對其的簡化需要新的條件.

方程(37)顯然存在一個平庸的非相干解αn≡ 0,對應于耦合振子的非同步態.隨著耦合強度的增加,耦合振子會產生同步,整體運動在相空間也會塌縮到一個低維空間中.在廣義序參量空間來看,系統也必然會在低維空間運動.根據協同學原理,這些廣義序參量中可能只有少數為慢變量,其余為快變量,其中慢變的廣義序參量會成為系統狀態的真正序參量.由于快變量的變化都依賴于慢變量,因此在發生同步轉變的區域附近,各階序參量之間應存在一定的關系,它們均依賴于慢變的序參量.一種最簡單的可能情形是所有的各階序參量αn都依賴于α1,不妨設為αn=G(α1,n).將其代入運動方程(37)中并比較每一階函數的傅里葉展開系數可以得到[56]

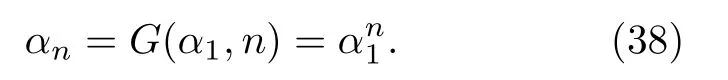
則(37)式的多個運動方程可簡并為單一方程,

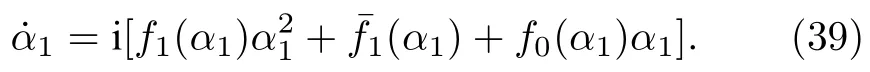
(38)式正是Ott-Antonsen(OA)擬設(ansatz)[47,48].

4.3 Poisson和不變子流形

OA擬設有什么物理意義呢？下面通過討論分布函數來進行分析.

由于分布函數是2π循環變量相位的函數,可將其進行傅里葉展開,而展開系數即為廣義序參量αn:

一般來說,知道了各階傅里葉系數即廣義序參量αn,就可以利用上述求和來得到分布函數,通常這需要無窮階的傅里葉系數.

OA擬設認為相位分布函數ρ的傅里葉展開系數即廣義序參量αn相互之間并不獨立,且滿足冪函數關系:

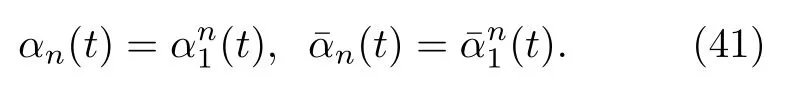
將其代入(40)式可以得到

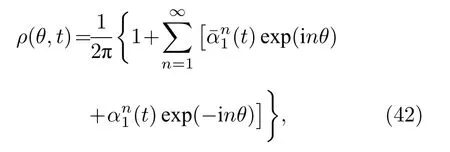
(42)式右邊的求和為冪級數,可以得到振子分布為泊松和形式

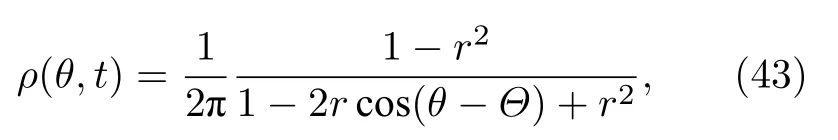
其中r為序參量α1(t)的幅度,Θ為集體相位.因而分布ρ(θ,t)完全由α1(t)決定.

由于具有關系(38)式的解滿足簡并的運動方程(39),則在動力學演化過程中形式(38)一直得到滿足.振子的分布雖然隨著系統的演化而改變,但將始終具有泊松和分布的形式.如果系統的初始相密度分布滿足泊松分布,那么不管在任何時刻系統的相密度分布將始終保持著這一性質.序參量關系式(38)式及簡并運動方程(39)被稱為動力系統的Poisson和不變子流形.這個不變子流形一個很重要的特點是雖然α1(t)可以不含時,也可以含時,但分布形式隨時間演化保持不變.這一結果將Kuramoto自洽理論僅僅討論定態的結果拓展至一般情形.

4.4 非全同振子系統的OA擬設

對于振子非全同的情形,若振子自然頻率各不相同,即{γi=ωi},設它們滿足分布 g(ω).那么當N → ∞時,引入密度分布函數 ρ(ω,θ,t),廣義序參量相應寫為(32)式,其中 αn(ω,t)為 ρ(ω,θ,t)的n階傅里葉展開式,也可以理解為自然頻率在ω → ω + dω之間的局域序參量.利用連續性方程可以得到如下遞歸方程:

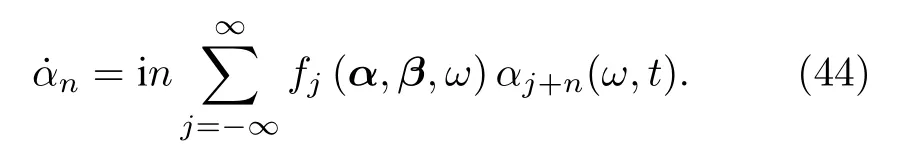
同樣如果耦合函數只包含一階傅里葉系數,則可以引入如下局域序參量的Ott-Antonsen擬設:

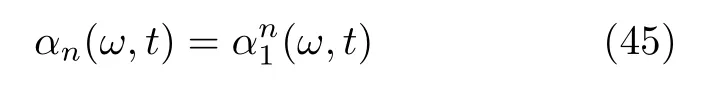
是方程(44)的一組特解.一階序參量為

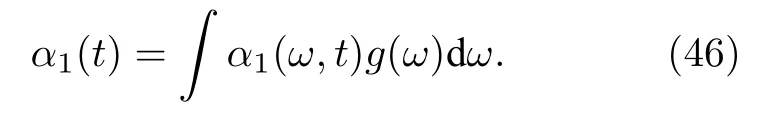
當分布函數g(ω)的形式為ω的有理分式時,可將ω從實軸延拓到復ω平面中去,在不引起發散的情形下(|α1(t)| ≤ 1)直接得到α1(t)的演化方程.

5 微觀動力學對稱性與Watanabe-Strogatz變換

耦合相振子系統在振子數 N ?1 時的微觀動力學研究會變得很困難.OA方法給出了一種有效的將高維耦合振子動力學降維的方案,但高維系統降維到二維的序參量空間來研究是有前提和成立條件的.

OA方法之所以成功,其關鍵在于Kuramoto系統本身的微觀動力學具有部分可積性.這要從1994年Watanabe和Strogatz的工作談起.他們研究了全局耦合約瑟夫森結方程(與Kuramoto模型系統同類).研究發現,N維方程中的每一條軌跡只能局限在一個三維子空間中,這意味著原始的高維微觀態可以通過一定方法降維至低維的宏觀態[46],這就需要他們提出的后來被稱為Watanabe-Strogatz(WS)變換的方法來實現.WS變換的提出在一定程度上為人們尋求高維動力系統的低維解提供了方向,但早期沒有引起人們足夠重視,且數學與物理意義均不明確.2009年,受Ott與Antonsen工作的啟發,Marvel等[49,50]成功將這類問題的解推廣到一般形式,給出了WS變換的數學意義,并清晰地給出OA擬設的數學依據.

5.1 WS變換

WS變換實際上來自于復數M?bius變換[57].定義復分數的M?bius變換 F :C→C 為

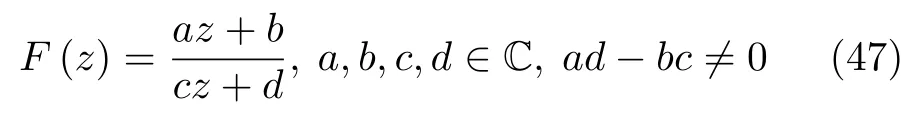
M?bius變換有很多很好的性質,其中之一就是存在且保持從直線到直線、從圓到圓的映射.由所有滿足上述條件的變換函數可以構成一個群,稱為M?bius變換群,

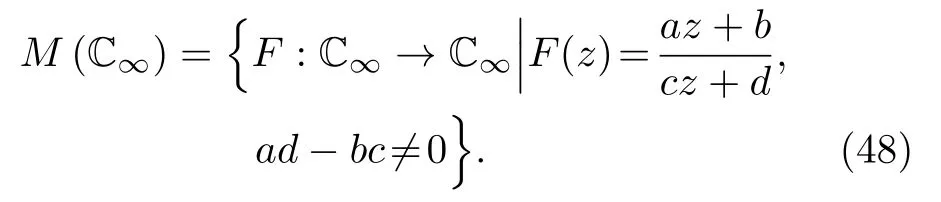
考慮一個子群,該子群包含了那些將單位開圓盤上的復數一對一地映射到自身的所有分數線性變換.

將耦合函數(36)式對應的動力學方程重新寫為如下形式:

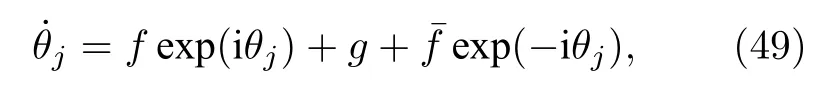
其中 j=1,2,··,N,f=f1(α)為光滑復函數,是其復共軛,g=f0(α)為實函數,它們均不依賴于指標 j.方程(49)定義了一個 N 維動力系統.Marvel和Strogatz[49]指出,方程(49)的解滿足如下 M?bius群在復空間內單位圓上的含時M?bius變換Mt:

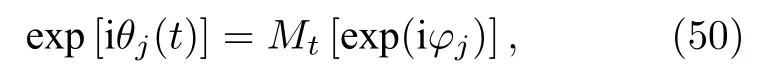
其中含時M?bius變換表達為

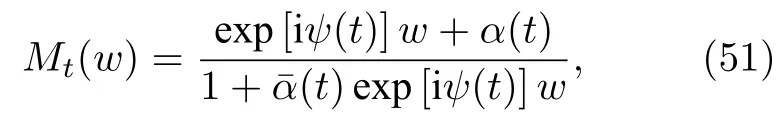
這里{φj,j=1,2,··,N}是系統的一組運動常數,ψ(t)是實參量函數,α(t)是復函數,| α(t)|≤ 1,ā(t)是α(t)的復共軛.(50)式和(51)式的變換就被稱為WS變換.對任意時刻t都對應一個變換Mt,這些變換構成的集合滿足群的性質,全體變換的集合{Mt}構成一個代數系統即M?bius變換群.系統(49)式的演化完全被變換(50)式和(51)式所支配.

5.2 三維動力學

方程(49)滿足變換(50)式和(51)式,說明了系統任一時刻的狀態{θj(t)}可由一組運動不變量{φj}在 WS 變換{α(t),ψ(t)}的作用下完全確定.而運動常數或不變積分{φj}的存在則反映了WS變換下系統的可積性.M?bius群本質上是一個三參量(ψ(t),Reα(t),Imα(t))的李群,相軌跡{θj(t)}被{ψ(t),α(t)}以及{φj}唯一地確定.

下面從代數方程出發去推導ψ(t),α(t)的運動方程.根據方程(50)有

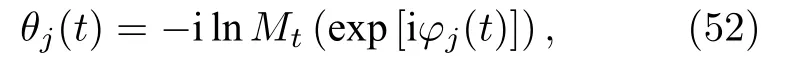
則對時間的導數為

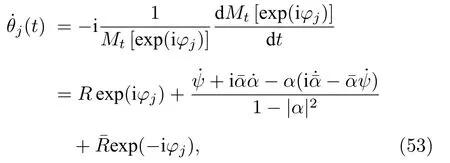
其中

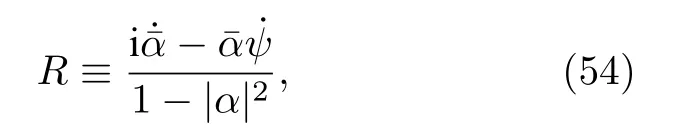
與(49)式對比可得

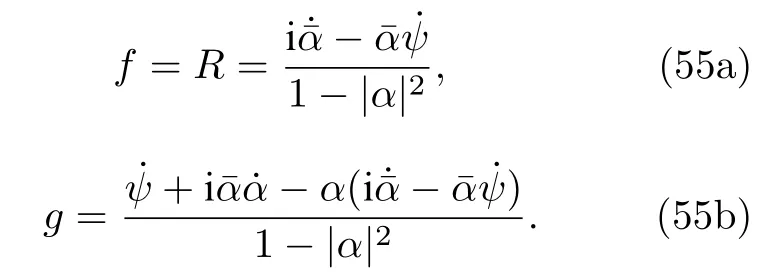
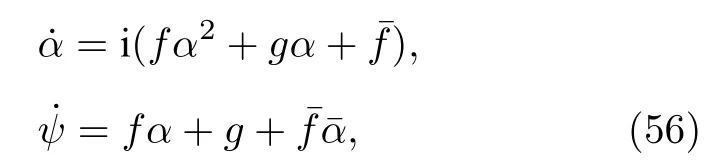
因此通過WS變換,可以將原始的N維相振子方程約化為三維的閉合方程,而振子數目N可以是有限的,也可以是無限大.

5.3 從WS變換到OA擬設

WS變換是一個從N維相空間向三維相空間的嚴格動力學變換.不同于統計方法例如基于序參量的OA擬設,WS方法并不依賴于任何近似條件或者特定狀態,而是將整個系統的動力學完整而嚴格地投影到低維系統中[56].當振子數N → ∞時,OA擬設下單一復序參量α1滿足的方程為(39)式,這是一個二維的閉合實方程.可以看到,WS變換下的三維方程(56)式中第一式即復序參量方程(39),因此一個自然的問題是,這兩者之間是否存在某種聯系？在什么情況下WS變換可以退化到OA擬設？下面來分析一下WS變換和OA擬設這兩種降維方案之間的區別和聯系.

對于N振子系統(49)式,通過WS變換可以將序參量α1(t)重新表示為

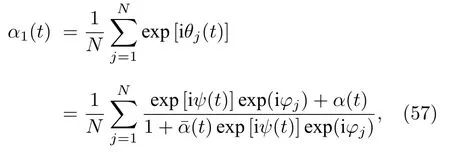
從一組不變量{φj}出發,若初始狀態已知,則系統的動力學情況可以由三維方程(56)描述.取特定均勻分布{φj=2π(j — 1)/N},則序參量(57)式可簡化為

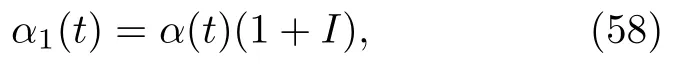
方程中

其中“—”對應于N為偶數的情況,“+”對應于N為奇數的情況.當 N ?1,I ?1,序參量就可以取近似 α1(t)≈ α(t).因而,當運動常數{φj}取均勻測度時,α1(t)與α(t)的方程完全一致,方程(56)中α(t)和ψ(t)的演化解耦,WS變換的三維方程流形退化到二維OA流形(39)式.

需要指出的是,當運動常數{φj}不取均勻測度時,α(t)和ψ(t)的時間演化就會相互耦合而無法簡單解耦,α(t)的動力學行為將會受到ψ(t)的影響,此時系統的動力學在三維空間中進行,α(t)和ψ(t)的運動會變得非常復雜[50,58].采用直角坐標,設α=x+iy,f=Ref+iImf,則三維方程(40)化為

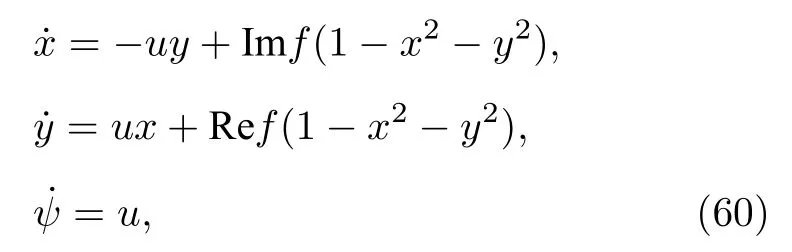
圖2給出了方程(60)的運動軌道在α平面的Poincare截面落點分布.可以很清楚看到在|α|比較小的區域均為環面,α的演化為定態或周期振蕩.但在|α|較大的范圍,運動軌道是不規則、混沌的[58].在環面區域,類似于哈密頓系統,環面對應于低維的運動,OA擬設可以成立.在混沌區域,α(t)和ψ(t)的演化相互耦合,OA擬設不適用.

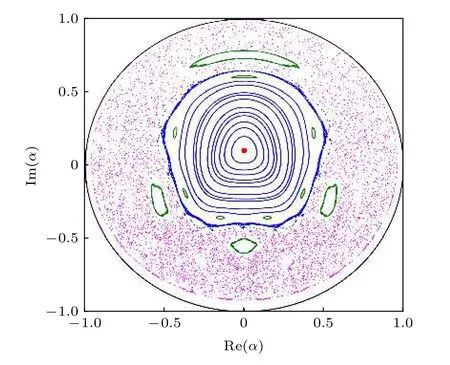
圖2 序參量α相空間的Poincare截面落點分布,可以看到閉合環面和混沌散點Fig.2.The Poincare section of the order parameter α in phase space,where one can find the closed tori and chaotic scattered points.

6 序參量理論在幾個同步問題研究中的應用

6.1 經典Kuramoto模型的同步相變

對于經典Kuramoto模型,即平均場耦合振子系統,Kuramoto已成功地通過自洽方程理論得到了臨界點及其臨界行為.下面利用OA擬設來研究該同步轉變問題.由于自然頻率非均勻,因此需用非均勻參數情況下的擬設.利用序參量

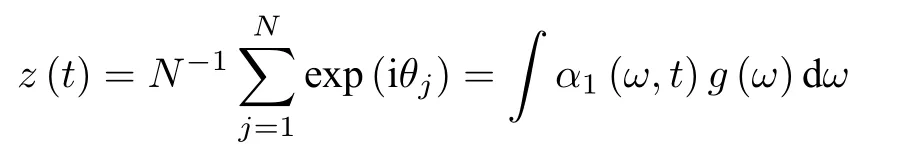
定義式可知,耦合函數中的分量分別為

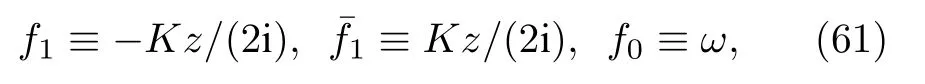
即Kuramoto模型耦合函數只包含到一階傅里葉分量.由(39)式可以得到

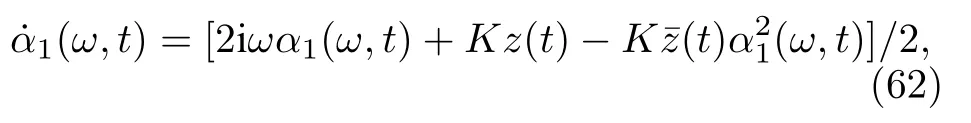
如果 g(ω)為 Lorentz 分布

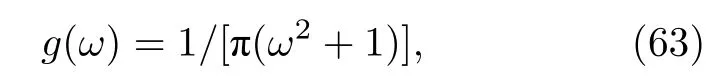
由(63)式有

(64)式的積分可以將ω延拓到復平面的上半平面進行,利用留數定理可以得到 z(t)=α1(ω=i,t),將其代入到(63)式和(64)式中有

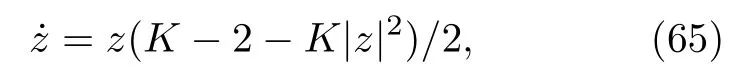
此即序參量滿足的動力學方程.這個復方程可以寫成振幅和幅角兩個實方程.可以看到,該動力系統存在臨界點Kc=2,當K ≤ Kc時,系統有唯一不動點 z ≡ 0,此即非相干態;當 K ≥ Kc時,z ≡ 0解失穩,系統分岔到新解

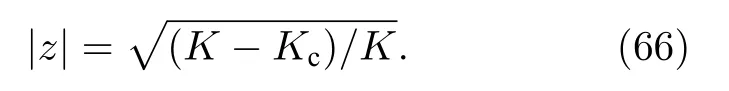
該解即同步解.對比Kuramoto自洽方程得到的結果可見,二者完全一致.

6.2 奇異態研究

奇異態(chimera state)是近年來發現的一類對稱性破缺導致的時空斑圖涌現行為,它描述了結構全同的單元(如相振子,其振子的自然頻率以及耦合方式都相同)在非局域耦合下會產生相干(coherence)和非相干(incoherence)共存的態[59,60].這種對稱性自發破缺的現象在很多生物系統中可以看到,例如海豚與其他海洋哺乳動物、遷徙的候鳥等都具有一類有趣的半腦睡眠現象[61],即它們可以在左(右)腦休息的時候讓右(左)腦保持清醒的狀態.人們在Kuramoto模型以及其他很多振子系統特別是神經系統中均發現了奇異態[62-67],并在光學混沌實驗[68]和化學Belousov-Zhabotinsky(BZ)反應實驗[69]實現.

結合相振子系統,我們考慮如下的空間一維Ginzburg-Landau方程

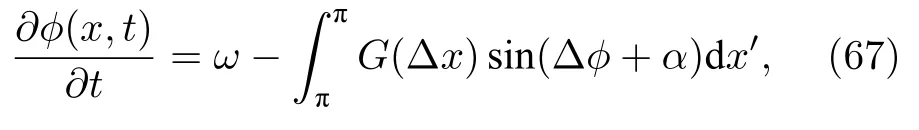
這里φ(x,t)為t時刻位于空間x處振子的相位,ω為振子自然頻率,設為空間均勻且ω=0.積分代 表 空間不 同 位置振 子 間的耦 合,Δ x=x-x′,Δφ=φ(x,t)-φ(x′,t).α為振子間的相移(阻挫),設 0 ＜ α ＜ π/2.非負耦合核函數 G(x)≥ 0 反映空間不同位置振子之間的非局域相互作用,通常設為歸一化且隨|x|增加而衰減的偶函數:

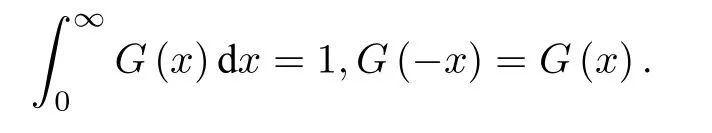
下面用OA擬設方法來研究系統(67)式的奇異態動力學[62,70,71].設振子分布函數為f(x,φ,t),它滿足連續性方程

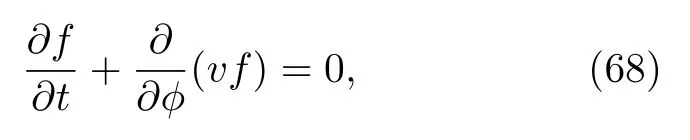
其中相速度為

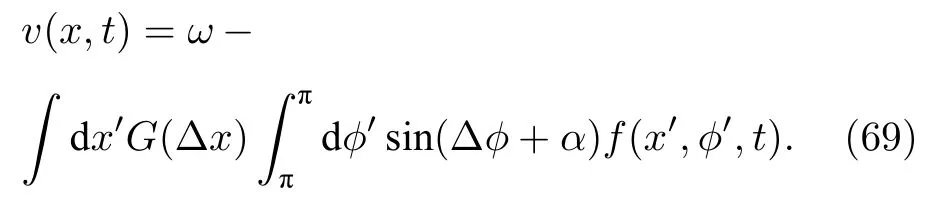
復序參量 Z(x,t)可表示為

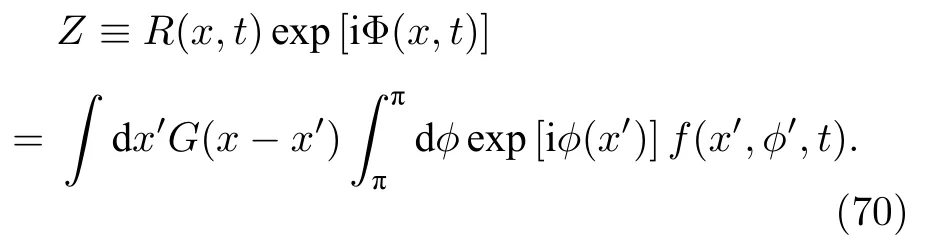
利用序參量表達式(70)式,(69)式的相速度v(x,t)可表示為

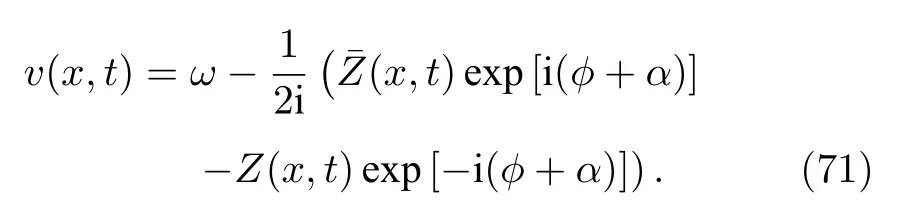
考慮到相位φ的2π周期性,可將分布函數表為相位φ的傅里葉級數形式:

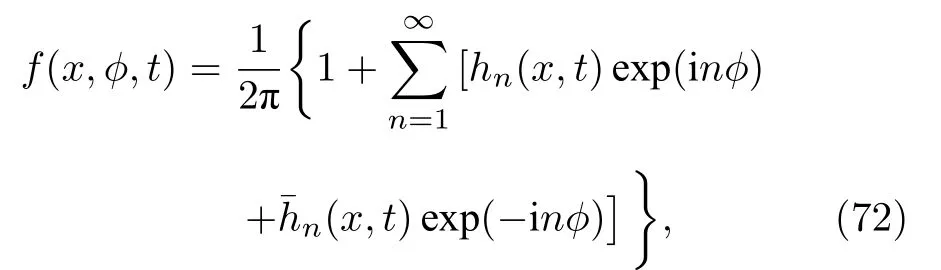
利用OA擬設[47],系數hn相互之間不獨立,它們滿足冪律關系:

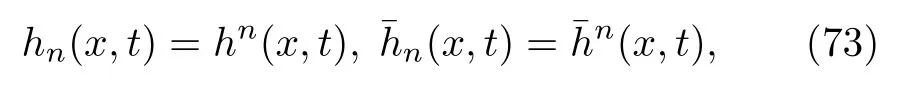
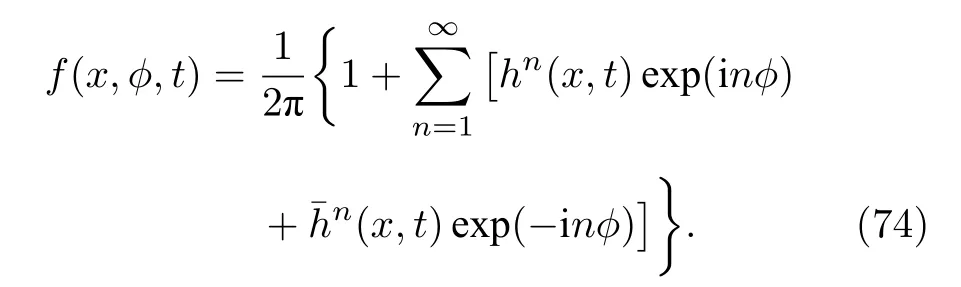
將(74)式代入連續性方程(68)式,并比較兩邊exp(iφ)的不同階系數可得

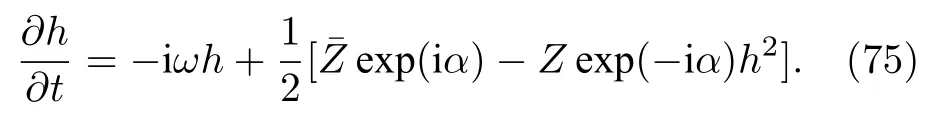
利用(74)式也可將序參量重新表達為

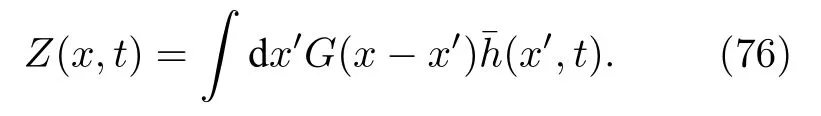
利用(75)式和(76)式可得到序參量的演化動力學行為.位于x處振子的相位長時分布函數為

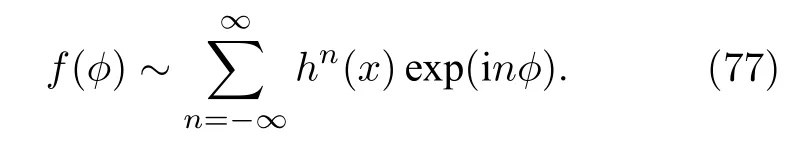
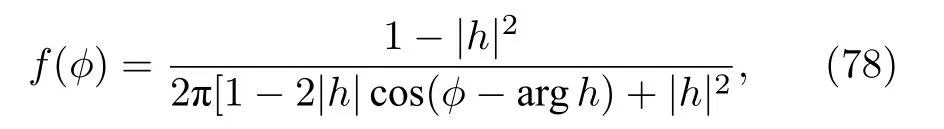
此處arg代表復函數h的幅角.上述分布函數為與(43)式形式相同的Poisson核函數,其中心位于argh處,|h|刻畫分布的非均勻性.當|h|=0時,f(φ)為均勻分布;當0 ＜ |h| ＜ 1 時,f(φ)為單峰分布;當|h|=1時,由于分布(78)式分子分母均趨于零,可求極限得 f(φ)簡并為 δ函數 f(φ)=δ(φ — argh),它代表所有振子的鎖相.

系數h(x,t)也可以看作是在空間x處exp(iφ)的統計平均,即

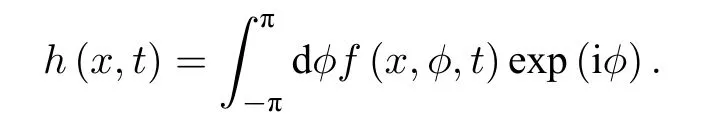
與(70)式定義的序參量Z(x,t)相比較,h(x,t)沒有對空間的積分,即沒有考慮非局域效應.因此h(x,t)量度的是空間x處附近的同步相干性,是一種局域序參量.若對某一x處有|h(x,t)|=1,則在(x- ε,x+ ε)(ε? 1)范圍內的振子會處于鎖相(相干態),而當|h(x,t)| ＜ 1 時,則在(x- ε,x+ ε)范圍內的振子處于非相干態,以此可以給出兩種態共存的奇異態.

在定態情況下,進一步利用(76)式可以得到序參量R(x)的自洽方程,進一步可以確定其空間分布.當然,也可用Kuramoto自洽方程理論來進行討論,可以得到與上述OA方法在定態時一致的結果.進一步的計算需要借助于數值方法,詳細討論可見我們的專著[51]與綜述文章[59,60].

6.3 高階序參量及其動力學

很長時間以來,人們聚焦于Kuramoto模型中的簡單耦合函數情形開展研究.在多數情況下,振子間相互作用并不是簡單的一階正弦耦合函數.對于一般的耦合函數,在第4節中已經看到,不同階序參量之間是復雜的相互依賴關系.Daido[72]早在20世紀90年代初就通過對一般耦合函數的Fourier展開提出了廣義序參量,但沒有進一步討論不同序參量之間的關系,而是使用傳統的Kuramoto自洽方程方法進一步討論.Pikovsky和Rosenblum[73]討論了如下具有相同自然頻率耦合振子的Kuramoto-Daido模型:

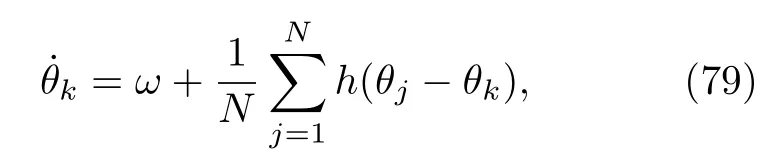
并引入了高階序參量{αn}.Pikovsky在該工作中早于Ott等[47]提出了序參量之間的依賴關系(擬設條件),即高階序參量{αn,|n| ≥ 2}均依賴于α±1.把(79)式中的耦合函數寫為Fourier級數形式,則動力學方程可寫為

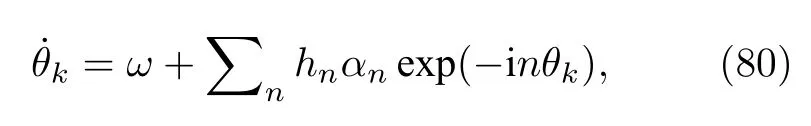
其中{αn}為(27)式定義的廣義序參量.考慮只有其中第l階Fourier分量耦合的情形,則動力學方程可寫為

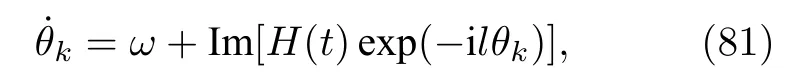
其中H(t)依賴于序參量αl.

下面討論利用WS變換來進行理論分析[74].動力學方程(81)可以重新寫為

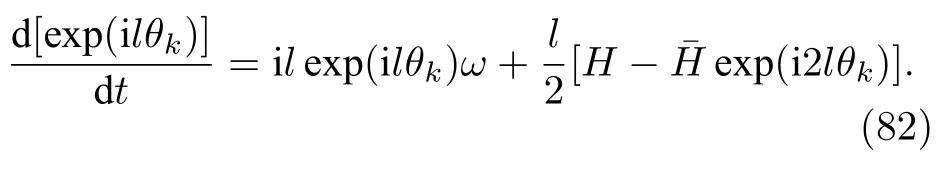
注意到M?bius變換不唯一,而其逆變換唯一,則利用M?bius逆變換

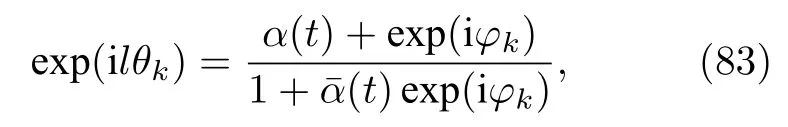
(83)式可變換為{φk},α及其時間導數

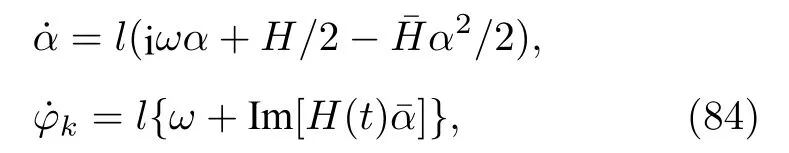
可以看到{φk}的方程右邊不依賴于k,說明變換后的相角{φk}均以相同角速度運動,因此可引入新變量為一組運動常數.顯然說明M?bius變換映射可寫為

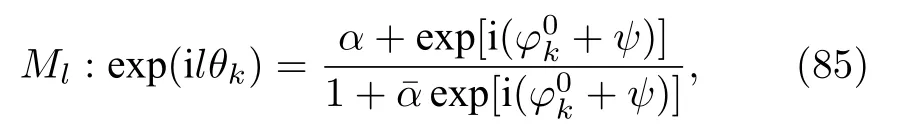
與一階耦合函數相比,這里形式上只是多出了l因子.

很多具體問題可以應用上述結果加以討論.例如近年來得到關注的三體相互作用平均場振子系統[75,76]

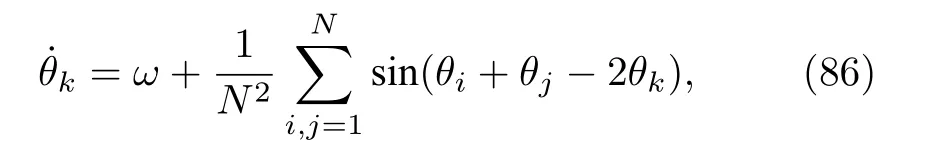
該系統對應于方程(81)中l=2,H(t)=α12的情形,因而可利用序參量方程(84)進行討論.

再例如具有阻挫的二階簡諧耦合振子系統[58]

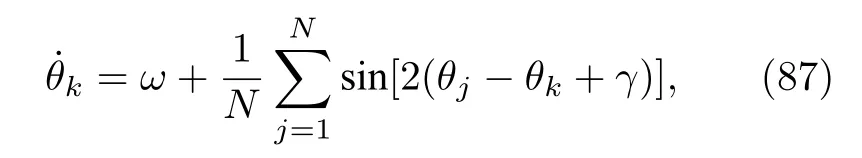
7 結 論

綜上所述,大自由度復雜系統的同步是一類典型、基本的涌現行為.這種涌現行為的出現是大量個體或自由度共同參與、通過相互作用自組織形成的整體有序.有序意味著復雜系統低維宏觀行為的出現,它往往是以序參量的出現作為標志的,可借助于統計物理學思想和方法來加以研究.就序參量的涌現機制來看,協同學的理論與方法揭示了大量自由度的復雜系統如何通過內部自組織與競爭產生出有序,其中非常重要的理論任務就是對復雜系統通過集體變量的分析來甄別快慢變量,并利用支配原理來進行降維,得到序參量的動力學.降維方法的精髓在于尺度的可分離性,特別是時間尺度的快慢可區分性,這種特性可以其他形式體現出來,如拓撲流形中中心流形的出現、變量中守恒律的存在等等.

在復雜系統同步的序參量動力學理論方面,除了Kuramoto的建立和求解序參量滿足的自洽方程方法以外,Ott和Antonsen提出的擬設是近年來應用較為廣泛的方案,該方案首先引入集體坐標即各階廣義序參量,然后通過各階量之間的非獨立性來達到降維的目標.這里面就隱含了絕熱消去快變量的思想.需要指出的是,OA擬設在很多情況下是一種推測,且在很多情況下不只是一階序參量是慢變量,另外的高階序參量也可能是慢變量,這需要從原始的各階序參量方程出發,利用協同學基本原理來進行分析.

下面討論一下對于實際系統同步作為整體動力學的研究分析.利用序參量動力學對同步的研究既可以是理論建立模型的研究,也可以是對實際問題利用的降維方法進行研究.相比于基于模型的理論研究,對于實際復雜系統有序行為的序參量動力學重構和研究顯然有著更為重大的意義和價值.對于很多實際中的復雜動態系統,在宏觀層面構建其序參量動力學是可能的,但也富于挑戰性.序參量動力學對實際問題的研究是通過采集微觀數據,然后在此基礎上進行宏觀動力學重構,因而是一個跨尺度動力學重構問題,迄今為止這仍然是一個開放的領域,與復雜網絡重構研究具有同樣重大的價值,是對復雜系統動力學方面的重要探索范式,值得大力開展研究.就本文討論的相位動力學及其同步而言,其目前在應用方面的主戰場之一是神經與腦科學[84].我們不妨以此為例進行說明.神經元的主體微觀動力學是電信號的積累發放,目前實驗方面已經可以采集大量實時數據并進行分析整合.對于腦電波及其各種動力學協同行為的研究,可以先抽取不同部位采樣的脈沖時間序列,再定義對應的相位,就可以建立相位的時間序列信息,據此計算不同序參量,通過分析序參量的低維行為進行討論.就目前的研究來看,很重要的一個課題是序參量動力學模型的重構,這一問題至今無論在神經科學還是其他領域都還沒有很大的突破,但已有一些具有啟發性的研究思路.例如,Zhang等[85]和Chen等[86]近幾年提出了主超前相位方法、動力學權重因子方法以及網絡動力學重構方法,以此可以分析復雜系統的動力學并結合序參量層次的動力學描述,完全有可能提供一個可行的圖景.這些工作還需要大力推進.