卡西米爾力*

苗兵

(中國科學院大學材料科學與光電技術學院,北京 100049)

量子電動力學中的卡西米爾力是真空零點能的體現.廣義的卡西米爾力則依賴于漲落介質的類型廣泛地出現于物理中,包括量子,臨界,戈德斯通模,以及非平衡卡西米爾力.長程關聯的漲落介質和約束是產生卡西米爾力的兩個條件.本文通過回顧卡西米爾物理的發展,討論了不同類型的卡西米爾力,幾種正規化方法,并對卡西米爾物理的進一步發展做了展望.

1 引 言

在一個具有長程關聯的漲落介質中引入外加約束,由于約束對于介質漲落模式的修改,因而在介質之間產生一種有效的相互作用力,即卡西米爾力(Casimir force)[1].在物理中,存在多種機制可產生長程關聯的漲落介質.例如,在量子場論中,規范對稱性要求零質量波色子,其傳遞的相互作用是長程的,這樣,零質量波色子場是滿足卡西米爾力產生要求的長程關聯漲落介質,典型的例子是量子電動力學中的電磁場(光子場).在統計物理中,調整參數至連續相變的臨界點時,序參量的關聯長度發散,序參量臨界漲落的關聯函數是長程衰減的冪函數,這樣,序參量場提供了產生卡西米爾力的長程關聯漲落介質;另一方面,即使不在臨界點,對于具有連續對稱的統計模型,由戈德斯通定理(Goldstone theorem)可知,破缺連續對稱可以產生零質量的戈德斯通粒子,因此戈德斯通場也提供了卡西米爾力產生的背景介質,典型的例子如鐵磁相變的n-矢量模型、超流相變、液晶、薄膜或界面、聚合物等.在非平衡體系中,動力學滿足的流守恒可以在非平衡體系中產生長程關聯,從而可以產生卡西米爾力.由此可見,卡西米爾物理是一個涵蓋廣泛的研究題目[2].

本文從卡西米爾力最初在量子電動力學中的提出,到廣義的卡西米爾力,對卡西米爾效應進行考察,最后對卡西米爾物理在未來的發展進行展望.

2 量子場論

2.1 發 現

量子場論中的卡西米爾力最早是由荷蘭物理學家Hendrik Casimir在1948年發現的[3].由于量子力學的不確定性原理,真空非空,而是充滿了量子漲落.量子漲落導致非零的真空能量,物理上稱為真空零點能(zero point energy of vacuum).卡西米爾力是真空零點能存在的一個直接結果[4].

Casimir考慮在真空中引入兩個平行的中性理想導電金屬平板,要求平板是無窮大和無窮薄的.金屬板的存在修改了真空中電磁場的漲落模式.Casimir分別計算了自由真空的零點能和加板約束后真空的零點能,發現兩者都有紫外發散,然而通過計算兩者之差,Casimir得到了一個隨著板間距離變化的有限能量,進一步計算該能量對板間距離的變化率,則得到兩板之間的一個吸引力,即著名的卡西米爾力,公式如下:

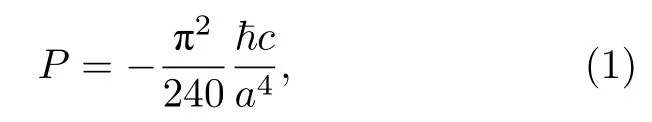
(1)式是兩板之間單位板面積的力,即卡西米爾壓力.式中,a是板間距離,?和c分別是普朗克常數和光速.由(1)式可以發現:(1)式中不出現金屬板的細節性質,而是僅依賴于物理學基本常數 ?,c,以及板間距離 a,因此卡西米爾力具有普適性;對于 ?和c的依賴說明卡西米爾力的產生是由于量子效應和相對論效應;卡西米爾力是隨板間距離以冪率(—4)衰減的長程力;負號表明這里的卡西米爾力是吸引力.

由于卡西米爾力的普適性,可以基于簡單的量綱分析(dimensional analysis)迅速得出(1)式的冪率關系.考慮兩塊平行的金屬板(Casimir平板),由于卡西米爾力P歸因于量子效應和相對論效應,因此P與 ?c成比例.由量綱[?c]=E·L,[P]=E/L3； 本問題里唯一剩下的長度尺度是板間距離a；由量綱分析得出: P ～?c/a4.可是,簡單的量綱分析無法得出卡西米爾力普適常數的大小和符號,確定普適常數需要做具體的計算.在下文中我們將給出卡西米爾力基于真空零點能的計算.

2.2 與范德瓦耳斯力的關系

本節敘述卡西米爾力的研究背景,講述其如何起源于對分子間范德瓦耳斯力(van der Waals force)在長程或者retarded情形下的計算[5],以及卡西米爾力在后來的發展中遠遠超出了范德瓦耳斯力的范疇.

對膠體穩定性問題的研究啟發了Casimir關于卡西米爾力的計算.膠體體系的不穩定性是由分子間相互作用力驅動的.理想氣體的狀態方程由于沒有考慮分子間相互作用而不能描述氣體的凝聚相變(氣-液相變).荷蘭物理學家 van der Waals將理想氣體方程修改為van der Waals方程,可以描述相變.在這個修正中,van der Waals引入了氣體分子的尺寸(排除體積效應)和氣體分子間相互作用力(范德瓦耳斯力).對于中性的氣體分子,范德瓦耳斯力是一種短程的吸引力,它將驅動氣體狀態的失穩而凝聚成液態.兩個中性(可極化)分子間范德瓦耳斯力的量子力學計算是由London完成的,稱為色散力(dispersion force),其原因是計算里需要考慮極化率(polarizability).

London的計算發現: 兩個中性分子間的色散力表現為一個以 r-6衰減的吸引相互作用勢,其中r是分子間距.粗略來理解,指數為—6是由于: 該力是分子的誘導偶極-誘導偶極相互作用,由于量子漲落,分子1產生誘導偶極,誘導偶極產生的誘導電場 E ～1/r3,分子2在電場E作用下產生誘導偶極 p ～αE～1/r3,這里α是分子的極化率,相互作用能 V ～-p·E～-1/r6.

Derjaguin-Landau-Verwey-Overbeek(DLVO)將London的色散力引入了他們的膠體穩定性理論.當膠體間由分子色散力帶來的吸引大于由靜電帶來的排斥時,膠體體系將失去穩定性而發生凝聚.在膠體穩定性的研究中,Verwey和Overbeek發現,實驗中分子之間的吸引力比1/r6衰減的更快,實際上應該是 1 /r7.Verwey和Overbeek 因此評論說,這是因為在London理論里,沒有考慮相對論效應,而膠體的間距(微米尺度)相對于微觀的分子尺度很大,因此需要考慮相對論修正.

Casimir接受了這個建議,與Polder合作,重新研究了London理論,加入了相對論效應帶來的所謂 retardation 效應,推導出了分子間的Casimir-Polder相互作用,是 r—7的色散吸引力.之后,Casimir認為Casimir-Polder分子間力的計算過于復雜,他希望簡化計算.在與玻爾(Bohr)談論時,玻爾評論這個力應該與零點能有關.受到啟發后,Casimir完成了兩宏觀平板之間卡西米爾力的計算,通過計算真空零點能得到了著名的卡西米爾力公式(1)式.

卡西米爾力被提出的時候,并沒有引起很大的關注.這可能是因為當時人們已經知道了兩個中性分子之間的色散吸引力,因此當中性分子變成兩個宏觀中性板時,其間會產生長程吸引力似乎并不值得過于驚訝.然而,我們需要指出,卡西米爾力為什么是吸引力,至今仍然沒有完全令人滿意的解釋.在后來的發展中,人們發現取決于漲落介質的類型,邊界條件,約束的性質和幾何,卡西米爾力可以是排斥力.實際上,對于一個具體的體系,在未做計算前,人們不能判斷卡西米爾力是吸引還是排斥力.因此,在卡西米爾物理的發展中,卡西米爾力雖起源于分子間范德瓦耳斯力的研究,然而其發展已經遠遠超出了分子間力的研究范疇.并且,在討論宏觀或者介觀物體之間的力時,人們通常將卡西米爾力和范德瓦耳斯力進行區分: 范德瓦耳斯力是短距離,近程的作用力,依賴于作用物體的分子細節;卡西米爾力是長程作用力,長程特點將分子細節平均掉,表現出普適性.

下面,我們不做具體的量子力學計算,而是利用標度討論(scaling argument)得出兩個中性分子之間的色散力,包含London的不包含相對論效應的non-retarded情況和Casimir-Polder的考慮相對論修正的retarded情況[1].

考慮兩個體積分別為V1和V2的中性分子,其電子運動的特征頻率是ω0.基于標度分析,間距為r的兩分子間相互作用勢能應采取如下形式:

其中,負號是因為吸引力,r-6是基于兩個體積乘積的量綱,? ω0是體系的特征能量,c/ω0是體系的特征距離,f(x)是一個無量綱標度函數,用于在non-retarded和retarded兩種情形之間進行過渡.

I)在短距離時,即 r ＜(c/ω0),兩分子之間的信號傳遞時間小于特征時間,不需要考慮相對論效應,取 f(x)=(常數,這)樣就得到London的結果:V(r)≈ -?ω0V1V2/r6.

II)在長距離時,即r ＞(c/ω0),兩分子之間的信號傳遞時間大于特征時間,需要考慮相對論效應.此時相互作用勢應不再依賴于表征特征時間的 ω0,為了抵消掉 ω0,取 f(x)=1/x(,這樣就)得到Casimir-Polder的結果: V(r)≈-?cV1V2/r7,其中,光速c的出現體現了相對論效應.

3 計 算

本節給出幾個用零點能計算卡西米爾力的算例,并且對其中處理發散的正規化方法(regularization)進行介紹.

3.1 一維空間標量場

首先考慮一個簡單的情形: 一維空間的零質量標量場,受限于兩點之間,取狄利克雷邊界條件(Dirichlet boundary condition)引入約束,點間距為a.

由量子場論,量子化的標量場可看作為一組振動的諧振子.由量子力學,基態或真空態下,頻率為ω的諧振子具有零點能 ? ω/2 .標量場的零點能為所有頻率諧振子的零點能之和.受限情形下,由邊界條件知道,允許的頻率為: ωn=ckn,這里,kn=(nπ)/a,n=1,2,3,…

計算標量場真空能量:

顯然,該無窮級數求和發散.為了處理發散,需要對(3)式進行正規化.有多種正規化的方法,這里,我們采取以下兩種方法.

3.1.1 衰減函數法

引入衰減函數f(n,x)=exp(-kn/Λ),這里,x=Λ-1＞ 0 .函數滿足:f(n,0)=1;f(n,x ／=0)→0,當 kn? Λ.因此有:

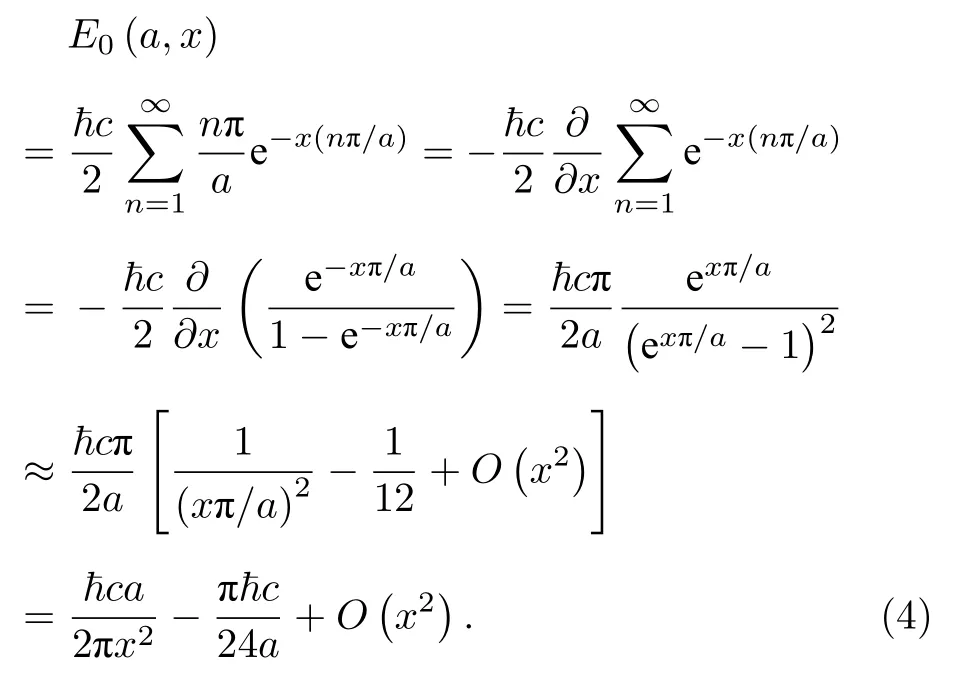
對于x≠0,(4)式給出正規化的有限大小真空能量.在正規化方法里,令x → 0,顯然首項發散,第二項是有限項,而高階 O(x2)→0 .

如何處理發散的首項呢？需要減去標量場的自由真空能,這是重整化操作(renormalization).下面計算自由真空能.

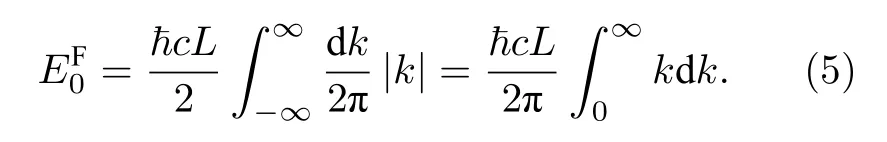
顯然積分發散,現引入衰減函數f(k,x)=exp(-xk)做正規化,這里 x ＞ 0.有

其中,Γ(x)是伽馬函數.因此,在有限區間內的自由真空能為

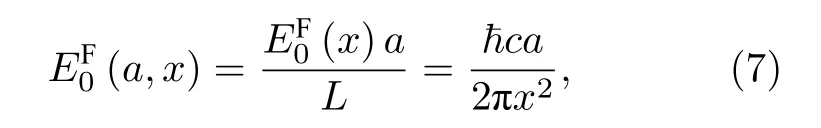
可發現,該結果正等于受限真空能(4)式的首項發散項.現在計算正規化卡西米爾能量:

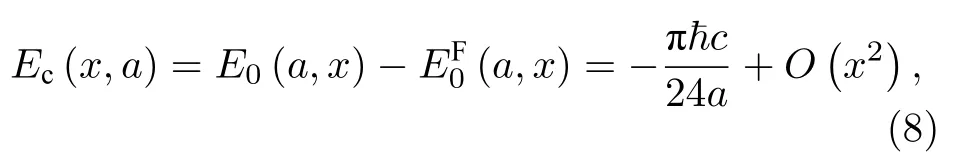
取極限x → 0,得到卡西米爾能量:

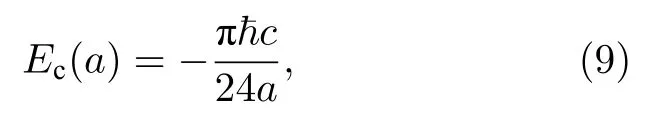
計算卡西米爾力:

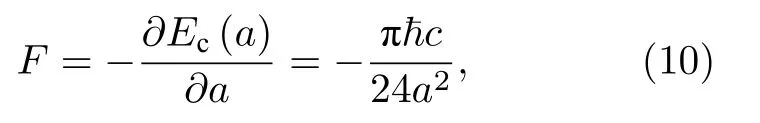
這是一個長程吸引力.由該結果可以看出:

1)結果僅依賴于基本常數 ?和c,以及約束間距a,與微觀細節無關,因此卡西米爾力具有普適性;

2)由于普適性,標度關系a-2可由量綱分析直接得到,因為 [ ? c]=E ·L,[ F ]=E/L,a是本問題的唯一長度尺度,故有 F ≈?c/a2;

3)常數項的大小和符號,需要具體計算,這里的結果是常數項為負,故為吸引力,我們指出,依賴于場的類型、邊界條件、空間維度等,卡西米爾力可為排斥或吸引,需要進行具體的計算.

3.1.2 zeta 函數正規化

做正規化:

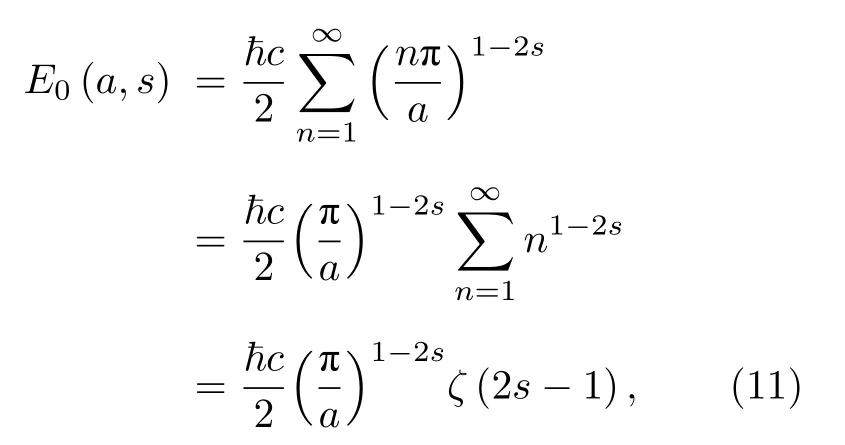
在正規化方法中取s → 0.利用解析延拓后黎曼 zeta函數的性質有ζ(-1)=-1/12,得 到同(9)式通過衰減函數正規化方法得到的結果一致.可以說,zeta 函數(不限于黎曼 zeta 函數)正規化是一種最優雅的正規化方法[6].

3.2 三維空間電磁場

本節研究Casimir對于真空中受限電磁場的計算.不同于Casimir采用的Euler-Maclaurin方法,我們用zeta函數正規化方法迅速得到結果.

在量子場論中,電磁場表現為一組諧振子自由度,真空中充滿了這些漲落模式.在真空中放入兩個Casimir平板,板面積為A,板間距為a.板的存在將漲落模式修改為:其中,n=0,±1,±2,··· .注意,不同于標量場的情況,這里n需要同時取正負整數,這是為了考慮電磁場漲落(光子)的兩個極化自由度,同時,模式(k⊥,0)可以被激發,即允許n=0.

計算受限的真空能:

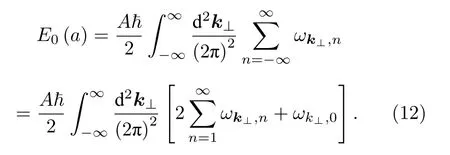
舍去與板間距a無關的項,得到Casimir 能量:

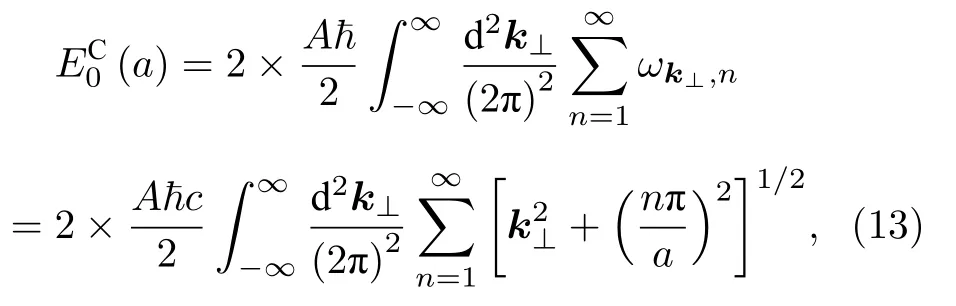
顯然,(13)式發散.現在引入正規化因子s,推導正規化的Casimir能量如下:

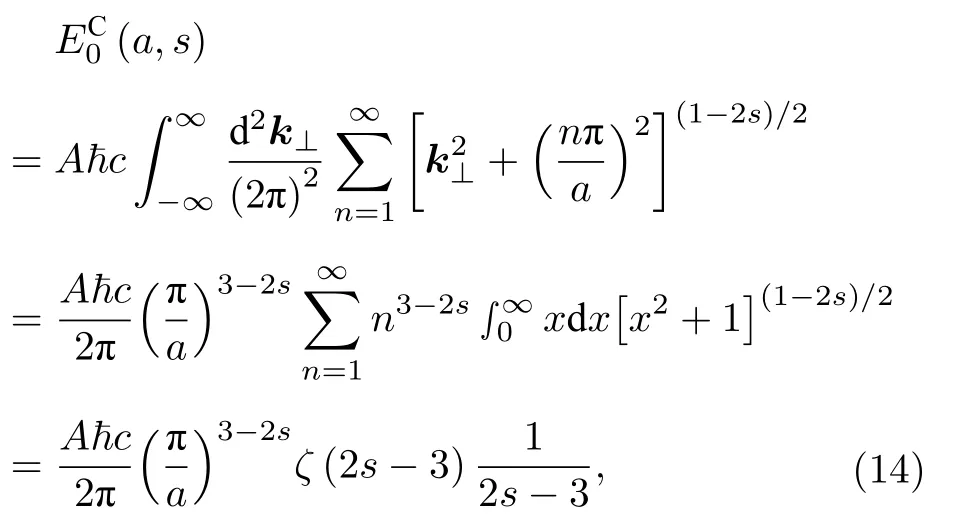
在(14)式的推導中,應用了黎曼zeta函數的級數定義,由級數定義的收斂性要求 R e(s)＞2 .并且在求無窮積分時假定了 R e(s)＞3/2 .

現在在正規化能量(14)式中取極限s→0,利用黎曼zeta函數的解析延拓,可得 ζ(-3)=1/120 .代入(14)式,得到單位面積的Casimir能量:

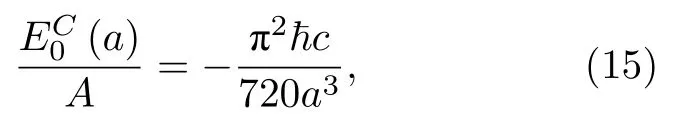
則Casimir力為

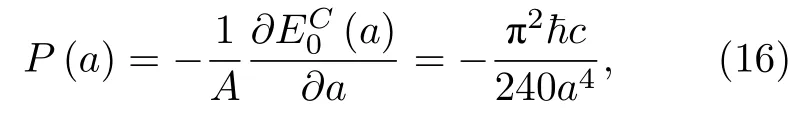
即(1)式.這樣就利用真空零點能推導出卡西米爾力,得到普適常數的數值.

4 臨界卡西米爾力

在連續相變的臨界點,序參量漲落的關聯長度發散,因此序參量場具有長程關聯,引入外加約束可以產生臨界卡西米爾力.1978年,Fisher和de Gennes考慮在兩元混合液體中引入兩個Casimir平板,即兩個平行的宏觀平板,調整參數至混合液體相分離的臨界點,此時序參量(液體濃度)具有長程關聯的臨界漲落,關聯長度ξ → ∞.由于兩板存在,漲落譜被修改,Fisher和de Gennes[7]認為兩板間產生臨界卡西米爾力.

臨界卡西米爾力具有普適性,我們再次用量綱分析研究該問題.由于溫度的存在,取代能量,需要研究體系的自由能F(a).自由能是一個廣延量,因此與板面積A成比例.序參量漲落是熱漲落,因此特征能量是熱能kBT.由于關聯長度在臨界點發散,問題里只剩一個長度尺度,即板間距a.由量綱分析,立即可以寫出:

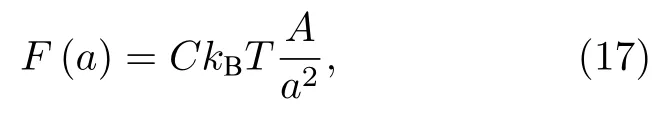
其中C是普適常數.

上述論證還可以按照統計物理中的Blob方法估算得出: 本問題的序參量漲落是熱漲落,因此可定義熱Blob,其能量為特征能量kBT;由于關聯長度發散,所以體系有唯一的特征尺寸a,故熱Blob的體積是a3;體系的Blob數目為g=(Aa)/a3=A/a2;體系的自由能為 F ≈gkBT=kBTA/a2.

和量子場論的情況一樣,普適常數C的數值需要通過具體的計算得出.一般來說,臨界卡西米爾力普適常數的計算比第3節中量子電動力學卡西米爾力的計算要復雜,這是因為電磁理論是一個線性理論,而這里的相變問題則是一個非線性的場論.計算過程需要使用臨界現象理論里發展出的d=4 — ε展開等技術.在兩維體系,由于體系在臨界點不僅具有標度不變性,并且進而有共形不變性,因此可以用共形場論的方法計算普適常數.另外我們指出,依賴于兩板上施加的邊界條件類型,臨界卡西米爾力可以是吸引或排斥力,即普適常數C可正可負[8].

5 戈德斯通模

由戈德斯通定理可知,體系在破缺連續對稱性時,將產生戈德斯通粒子(Goldstone particle)或戈德斯通模(Goldstone mode),這是一種零質量的模式,因此是長程關聯的.擾動戈德斯通模也會產生卡西米爾力.

統計力學里,戈德斯通模通常采用具有O(n)對稱的n-矢量模型進行展示.體系的序參量:ψ=(ψ1,ψ2,···,ψn).體系的哈密爾頓量對于序參量具有連續的旋轉對稱性.經歷相變后,體系發生自發對稱破缺,即序參量破缺哈密爾頓量的連續旋轉對稱,在n-矢量空間中自發選出一個方向排列,體系進入有序態.序參量的漲落模被分成1個平行于有序方向的縱向模式(軟模)和(n-1)個垂直于有序方向的橫向模式(戈德斯通模).由于戈德斯通模不需要耗能,因此是長程關聯的漲落.需要指出,縱向的軟模導致了體系的有序,其只在臨界點質量為零,軟模漲落導致的正是前面討論的臨界卡西米爾力.然而,不限于臨界點,零質量的戈德斯通模存在于整個臨界點以下.

下面以幾個軟物質物理中的例子來說明戈德斯通模誘導產生的卡西米爾力.1)液晶.液晶體系通常由棒狀分子組成,這一分子特點在統計問題中引入了取向自由度,即可以研究體系的連續旋轉對稱性.如上所述,這就為問題提供了戈德斯通模,進而戈德斯通模可以誘導產生卡西米爾力.2)薄膜或界面.由于薄膜或界面平面具有連續平移對稱性,因此破缺該對稱性會導致戈德斯通模,這里就是聲子(phonon),聲子導致薄膜或界面的毛細漲落(capillary fluctuations).在薄膜或界面上引入外界約束物,將修改體系的漲落譜,因而可以誘導產生卡西米爾力.3)聚合物.聚合物統計力學里的一個重要結果是de Gennes認識到聚合物的排除體積問題(對應于自回避無規行走)可以用自旋n-矢量模型的n → 0極限描述[9].如上所述,n-矢量模型有(n-1)個戈德斯通模,若考慮在聚合物熔體中引入兩個Casimir平板,計算戈德斯通模誘導的卡西米爾力:

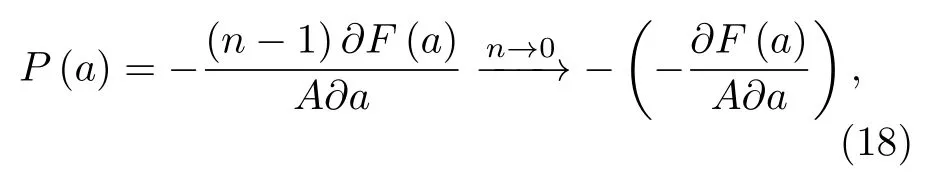
因此,聚合物漲落背景誘導的卡西米爾力與一般的卡西米爾力反號,如果一般的卡西米爾力是吸引力,則聚合物誘導卡西米爾力是排斥力[10,11].

6 實驗驗證

自量子電動力學的卡西米爾力在1948年提出后,引發了一系列的實驗工作來驗證卡西米爾力.先計算一下卡西米爾力的大小,由(1)式可寫出: P≈—1.3×10—5atm×(1 μm/a)4(1 atm=101.325 kPa).因此,當板間距a=1 μm時,卡西米爾力大約為1.3 mPa,這已經是一個宏觀的數值了.減小板間距離至微米以下,卡西米爾力以a—4方式增大.

經過這個估算,實驗上應該在微米尺度測量卡西米爾力.早期有一些定性的探測卡西米爾力的實驗工作[12]和一些高精度的實驗驗證[13,14].此后,由于卡西米爾力在微米尺度是不能忽視的作用力,因此出現了應用卡西米爾力的工作,主要是在微米尺度的一些金屬機器的制造上,稱為微米電力系統(microelectromechanical systems,MEMS)[15-17],這些微米尺度機器的應用研究導致的兩個重要的問題是: 1)由于卡西米爾力是吸引力,器件將被粘附在一起而無法正常工作,那么,如何實現卡西米爾排斥力;2)由于器件有不同的形狀,那么,如何計算超越Casimir平板的不同形狀器件之間的力.

臨界卡西米爾力的重要驗證實驗包括研究液氦薄膜在經歷超流相變時膜厚的變薄過程[18]和研究在兩元混合液體臨界點附近膠體與表面的相互作用[19].超流實驗有意思的地方在于臨界卡西米爾力和戈德斯通卡西米爾力將一起影響膜厚.在超流相變臨界點(Tλ)附近,序參量漲落變成零質量的臨界漲落,該漲落在液氦薄膜的兩個表面(固體銅片表面和液氣界面)之間誘導臨界卡西米爾吸引力,導致膜厚降低.在臨界點Tλ以下,臨界漲落消失,膜厚回升.可是實驗發現,膜厚沒有回到臨界點以上的數值,而是相對偏小,原因有兩個: 1)超流相變的序參量(位相角)漲落導致戈德斯通模,戈德斯通模誘導的卡西米爾吸引力使Tλ以下膜厚較臨界點以上偏小;2)薄膜的下表面是氦的液氣界面,在超流態,黏度為零,界面漲落的戈德斯通模(毛細漲落)誘導產生兩表面間的卡西米爾吸引力,進一步減小膜厚.兩種因素的聯合作用解釋了實驗的觀察結果[1].

7 一些發展

在卡西米爾力的處理中,有一些重要的假定.1)將外加約束與漲落介質的相互作用以施加的邊界條件處理.這種處理是基于體系中時間尺度的分離,即外界約束運動的特征時間遠遠大于介質漲落的特征時間.該處理本質上是在一個介質和約束的體系中,將約束的運動作為慢變量而固定,得到一個關于漲落介質的有效模型,而約束慢變量則影響介質的漲落譜.顯然,這種處理中,只有約束對于介質的作用,而沒有介質對于約束的反作用.2)在Casimir平板的邊界條件中,平板無窮薄,因此沒有考慮介質的穿透效應.

在卡西米爾力理論的發展中,針對不同的假定有后續的發展.Lifshitz[20]和Woods等[21]發展了Lifshitz理論,該理論將卡西米爾力推廣到實際材料體系,利用漲落耗散定理推導了麥克斯韋能動量張量,從而得出不同溫度下兩個平行的介電材料之間的相互作用力.Schwinger[22]利用自己的量子場論non operator版本,即源理論(source theory),重新推導了卡西米爾力,在該推導中沒有出現真空的零點能.隨著理論物理的發展,人們認識到產生卡西米爾力的約束,可以是來自外加邊界條件,也可以是在溫度場論中通過松原理論(Matsubara formulation)將溫度引入場論時帶來的周期性條件約束.在宇宙學中,還可以是在處理非歐空間(non Euclidean)時由無邊界空間的拓撲性質(topology)引入的“Identification”約束等.另一方面,在長程關聯漲落介質的尋找上,人們發現在非平衡統計體系里,動力學守恒率可以使非平衡體系產生冪率衰減的長程關聯行為,這使得非平衡體系,包括顆粒體系、活性物質等,成為另一個研究卡西米爾力的重要情形[23],需要指出,與平衡體系相比,非平衡體系的卡西米爾力不具有普適性.這些進展都是卡西米爾物理發展的精彩篇章.

8 結論和展望

本文討論了廣義的卡西米爾力.通過考察具有長程關聯的不同漲落介質,包括電磁場、臨界場論、戈德斯通模,以及非平衡體系,可以看出,卡西米爾物理涵蓋了物理學里寬泛的研究方向.在未來卡西米爾力的研究中,從基礎物理的角度,通過研究約束的不同實現和處理方法,以及研究不同種類的長程關聯漲落場的產生,卡西米爾力將會有一個更為寬廣的研究方向,并有希望通過卡西米爾力的概念,在不同的研究題目和方向之間建立聯系.從應用的角度,量子電動力學里的卡西米爾力是量子效應的宏觀反映,在微米以下器件的設計中,必須考慮卡西米爾力,并通過對其進行調控實現不同的應用功能,而臨界、戈德斯通、非平衡等熱卡西米爾力也可以用來調控統計體系中結構和序的形成.