復雜網絡上的部分同步化:奇異態、遙同步與集團同步*

王振華 劉宗華

(華東師范大學物理與電子科學學院,上海 200241)

近年來,復雜網絡上耦合振子的部分同步化引起了人們極大的關注,其潛在或背后的原因是部分同步化斑圖在大腦網絡中廣泛存在,并很可能與大腦的認知或記憶等功能有密切的聯系.本文對這些進展進行簡單的總結與歸納,并按照學者們研究的不同側重點,將其分成三方面來進行介紹,即奇異態、遙同步與集團同步化.著重強調這三種情形各自出現的條件、常用的研究模型、檢測的方法以及側重解釋的生物現象等方面.并對它們三者之間的相互關系及今后的研究方向做一些簡單的探討.

1 引 言

混沌通常被認為是有害的現象,直到1990年美國海軍實驗室的Pecora和Carroll[1]發現兩個全同的混沌系統實際上是可以同步化的,從而導致了混沌系統的一個極其重要的應用——保密通信[2].源于這個應用,兩個耦合系統間的混沌同步化受到了極大的關注,并發現了一系列的同步化方式,如完全同步、相同步、延遲同步及廣義同步等.隨后,這些研究被推廣到了多個耦合系統的情形,包括耦合映像格子的時空同步化等.這些同步化的一個共同特征是耦合的各子系統間行為一致,是作為一個整體來表現同步特征的.

實際上,除了這些整體同步化外,還存在著以非整體行為的方式體現的同步化.比如,在貓的視覺皮層中,分布在不同空間位置的神經元與它們的振蕩響應(40—60 Hz)是同步的[3].然而,這個現象直至十年之后,也就是2000年左右,才引起了人們的廣泛關注,被稱為部分同步化.部分同步主要討論兩個振子以上但總振子數目不是太大的情形.此時只有部分態變量是同步的,而其他態變量并不與它們同步,因此系統的軌道將收斂到一個由同步變量定義的不變線性子空間[4-7].比如考慮由三個振子 x,y,z 組成的耦合混沌系統,部分同步可以發生在振子x與y之間或x與z之間,而第三個振子并不與這兩者同步.部分同步化已獲得了實驗驗證[8,9].

上述研究,無論是同步還是部分同步,包含的子系統數目都不大,通常只有2—6個子系統.另外,這些耦合的連接方式是均勻的,比如最近鄰連接、規則連接或者全連等,而不涉及復雜的網絡結構,因此在理解大腦的各種同步斑圖方面幫助不大.最近,部分同步的研究有了長足的進展,不僅僅是子系統數目擴大到成百上千的規模,而且連接的方式也推廣到多種多樣[10,11],從分組連接到復雜網絡連接,甚至到了多層網絡連接[12,13].基于這些研究,人們發現復雜網絡上的部分同步可以展現出復雜多變、多姿多彩的斑圖,這就對大腦斑圖的多樣性給出了一種可能的機制.我們知道,大腦皮層的大尺度同步[14]與網絡神經元子集的同步放電[15,16]均與認知過程密切相關,且額葉腦區內任務相關的α波同步與頂底加工(top-down processing)的需求也高度相關[17].另外,神經活動的同步斑圖還與大腦無序緊密相關.比如,癲癇發作時,特定腦區會變得高度同步,其他部分則不同步[18].而在失去了部分腦細胞導致的帕金森氏病中,同步活動將會在特定的腦區缺失[19].因此,復雜網絡上部分同步化的研究為理解大腦的高級功能,如認知與記憶等打開了一扇新的窗口,亟待進一步深入下去.

由于復雜網絡上部分同步的復雜性,歷史上,不同的研究小組從不同的角度得到了不同的發現,并依據具體出現條件的不同而將其分別命名為奇異態、遙同步及集團同步等.奇異態是最先命名的,描述的是同步振子與無序振子的共存現象,可對半腦睡眠與首晚效應等生物現象做出合理的解釋.遙同步是最后命名的,描述的是不直接相連的振子之間通過中心節點發生同步但卻不與中心節點上的振子同步的現象,可用于幫助理解大腦分布式計算的內在機制.而集團同步化居中,描述的是復雜網絡上的部分振子因具有某種對稱性而形成同步集團的現象,可幫助理解大腦同步斑圖的多樣性.雖然這三種部分同步化狀態發現的初始時間略有不同,但對它們研究的進展并沒有絕對的先后,而是交替前行、相互促進的.實際上,這三種部分同步化狀態并不是完全獨立的,甚至有時描述的是同一種現象或斑圖.本文將對這些進展進行綜述,并對它們間的相互關系進行簡單的討論.

2 奇異態

奇異態描述的是同步與無序這一對矛盾體共存的特殊情形,是Abrams與 Strogatz[20]于2004年命名的.其英文名字為Chimera state,代表希臘神話中的一種獅頭、羊身、蛇尾的噴火怪物.這個名字取得非常好,不僅僅在于它把這個領域做“熱”了,更重要的是它描述了一大類生物系統半腦睡眠現象的微觀機制.來自于實驗探測的EEG數據表明,在一些鳥類與海洋哺乳動物的睡眠過程中,它們的一半大腦是同步的,而另一半大腦是非同步的,這就使得一半大腦比另一半具有更強的警覺性,從而減少睡眠時所受到的外部攻擊,稱為“半腦睡眠”[21,22].眾所周知,人類早期住在山洞而沒有房子保護時也需要提防野獸的攻擊,因而這種警覺性或許到目前應該還有某些殘留痕跡.這種推斷直到2016年才被實驗證實,稱為“首晚效應”[23].說的是當人們出差到異地時,第一晚的睡眠通常不踏實,而是表現為左邊半腦覺醒的次數要遠大于右邊半腦,但第二晚以后會恢復正常.

另一方面,奇異態的研究也拓展并豐富了非線性動力學及耦合振子理論.長期以來,人們一直相信同步與非同步的共存是限制在非均勻振子網絡中的,其中具有相似頻率的振子可以發生同步,而那些偏離平均頻率較大的振子則保持不相關的漂移.因此,當發現全同振子在相同的耦合方式下也可以分離成為同步與漂移的兩組,即奇異態時,就從根本上令人感到吃驚,因為全同振子通常是作為整體,表現為要么同步要么非同步的.這樣,作為一種新的動力學狀態的奇異態就實質性地拓展了我們對從同步到混亂的轉變或相反的轉變的認識.

事實上,奇異態這種現象在其命名的兩年前就由Kuramoto與Battogtokh[24]在Ginzburg-Landau方程中注意到了,但當時并沒有引起人們足夠的重視,這也從一個側面說明了命名的重要性.在這個發現中,一個極其重要的因素是,不同于以往的全局耦合或最近鄰耦合,甚至也不同于隨機耦合,作者采用了一種隨距離衰減的指數耦合,稱為非局域耦合(nonlocal coupling).雖然這種非局域耦合沒有局域或全局耦合那么受到重視,但它其實也有廣泛的應用,比如在約瑟夫遜結、化學振子、蝸牛殼模式的神經網絡及眼優勢條紋中等.Abrams與Strogatz[20]繼承了這個非局域耦合的思路,但代之以Kuramoto相振子模型.此外,他們還將指數衰減的耦合核改為余弦耦合核,使得模型可以解析求解.

研究奇異態最常用到的是Kuramoto相振子模型,這個模型因只含振蕩的相位特征卻沒有涉及振蕩的振幅而被認為是描述自然界各種振蕩行為最簡單的模型.Abrams與Strogatz[20]考慮的模型就是這樣一個相振子環,其方程為

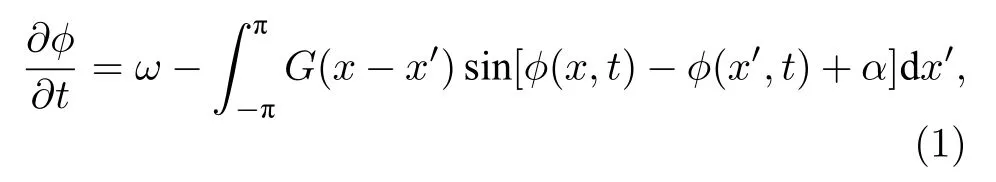
這里 φ(x,t)為振子在位置x時間t時的相,角度0 ≤ α ≤ π/2 為 可調參數.耦合核 G(x-x′)假定取如下形式:

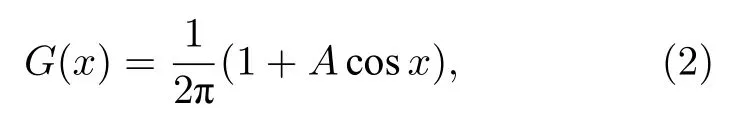
其中 0 ≤A≤1 .引入序參量來對局部振子的有序與無序進行描述.令Ω代表旋轉框架的角頻率,θ=φ-Ωt代表振子相對于這個框架的相,于是有

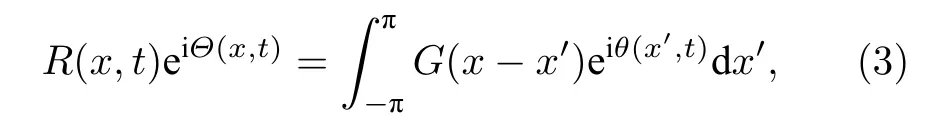
其中R為序參量,Θ為局部平均相.此時,方程(1)變為

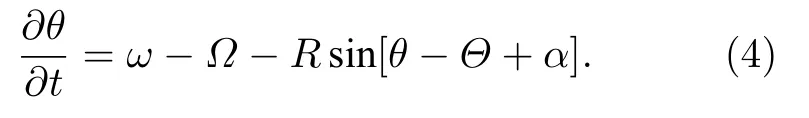
穩態時,R與Θ將獨立于時間,而只依賴于空間.作參數變換: β=π/2-α與Δ=ω-Ω .圖 1(a)為方程(4)的快照,其中靠近 x=±π 的振子是鎖相與相關的,即它們以相同的瞬時頻率運動并處于近似的同相.同時,圖1(a)中間的分散振子是漂移與無序的.圖1(b)則給出了對應圖1(a)的序參量曲線,證實同步態具有較高的R值,而無序態具有較小的R值.圖1(c)則為對應的局部平均相 Θ(x).

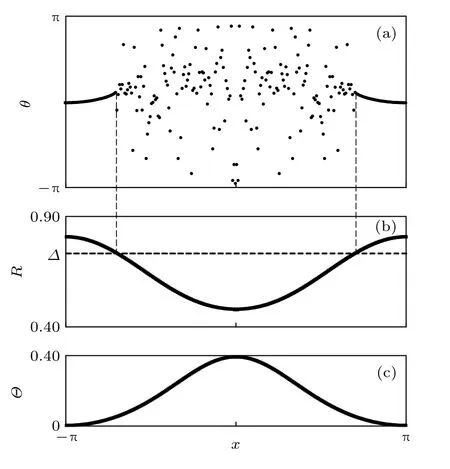
圖1 (a)奇異態的斑圖,參數: A=0.995,β=0.18, N=256個振子;(b)來自于方程(3)的局部相關聯 R(x),鎖頻的振子滿足 R(x)≥Δ;(c)局部平均相 Θ(x).改編自文獻[20]Fig.1.(a)Phase pattern for a chimera state,parameters:A=0.995,β=0.18,N=256oscillators;(b)local phase coherence R(x),computed from Eq.(3),locked oscillators satisfy R(x)≥ Δ;(c)local average phase Θ(x).Figure adapted from Ref.[20].

隨后,Abrams等[25]于2008年提出了一個僅包含兩組相互作用的振子集團且精確可解的奇異態模型.這個模型人為地將振子分成大小相等的兩組,各組內與組間的耦合方式完全一樣,通過初值條件選取的不同,使得它們一個處于同步態,而另一個處于無序態.通過Ott與Antonsen[26]的降維方法,他們得到了關于奇異態穩定性、動力學及分岔的精確解.其模型如下[25]:

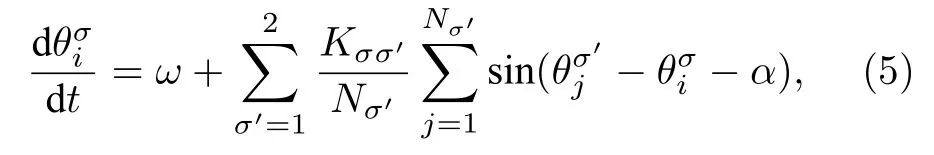
其中 σ=1,2,Nσ為第 σ 組內的振子數目.因假定全同振子,因此頻率ω與相延遲α對所有振子都是一樣的.組內的耦合強度設定為K11=K22=μ＞0,組間的耦合強度則取為K12=K21=v ＞ 0,且 μ ＞v,即組內的耦合大于組間的耦合.這有點類似于上面的隨距離衰減的非局域耦合.對時間做標度變換,可設定 μ +v=1 .進一步為方便尋找奇異態存在的區域,定義參數 A=μ-v與β=π/2-α.

對于隨機選擇的初值,方程(5)很容易走向同步態.但當初值設置在奇異態附近時,比如一組為近似同步的初值,另一組為隨機初值,則能觀察到奇異態[25].圖2為奇異態的動力學,只畫了非同步那一組的序參量,其滿足 r(t)=|〈eiθj(t)〉| .從圖2(a)—圖2(c)可見,對應不同的參數值A,序參量分別呈現常數值、小振動及大振蕩行為,分別表示穩定的奇異態、呼吸奇異態及長周期呼吸子.

當取其他的β時,也可能出現穩定的奇異態與呼吸奇異態,但所需的耦合強度差A會有所不同.借助于OA降維方法,Abrams等[25]得到了依賴于參數β與A的解析解,并給出了各穩定區域間的邊界曲線.圖3是相應的相圖.

上述奇異態一旦形成,便不再改變,因此是穩定的奇異態.為了實現海豚與鳥類在睡眠中出現的交替奇異態,Ma等[27]引入了一個周期性的延遲信號來描述變化的外部環境.具體做法是將方程(5)改寫為

其中A與Ω分別為外部信號的振幅與頻率,τσ代表系統對環境的響應時間.考慮到睡覺半腦與清醒半腦對外界應該有不同的響應,可令τ1=0與τ2／=0.耦合參數取為μ=5與v=-4.負耦合v=-4來自于組間的相互作用,不同于組內的相互作用,其依據是視交叉上核中左右振蕩組之間是反相同步[28].另外,由于真實大腦中神經元的非全同,可令ωi隨機均勻地分布在[1-δ,1+δ],其中δ代表振子的多樣性.Ma等[27]發現,對一個固定的δ,存在一個閾值A0,以便A≥A0時可以出現交替的奇異態.比如當δ=0.1時,有A0=0.2,且隨著δ的增加,A0會逐漸降低.圖4給出了N1=N2=128與δ=0.1時 的結果,其中圖4(a)代表A=1,Ω=1與τ2=1.5的情形;圖4(b)為A=1,Ω=0.5與τ2=1.5的情形;圖4(c)為A=1.5,Ω=1與τ2=1.5的情形;圖4(d)為A=1,Ω=1與τ2=3.0的情形.從圖4可見,交替奇異態存在于所有的四種情形中,表明交替奇異態對信號參數具有魯棒性.

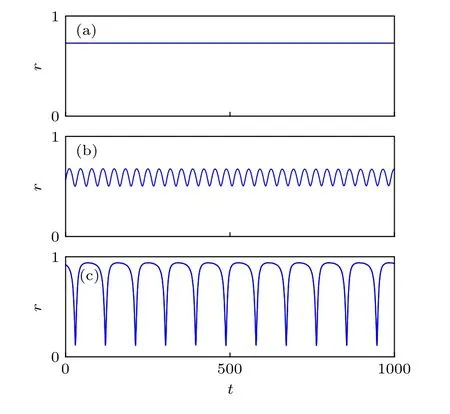
圖2 序參量r隨時間的變化,其中參數 N1=N2=128,β=0.1(a)A=0.20,穩定奇異態;(b)A=0.28,呼吸奇異態;(c)A=0.35,長周期呼吸子.初值條件取為靠近奇異態,結果為丟掉了2000個暫態時間單位后的情形.改編自文獻[25]Fig.2.Order parameter r versus time.In all three panels,N1=N2=128 and β=0.1 :(a)A=0.20,stable chimera;(b)A=0.28,breathing chimera;(c)A=0.35,long period breather.Numerical integration began from an initial condition close to the chimera state,and plots shown begin after allowing a transient time of 2000 units.Figure adapted from Ref.[25].

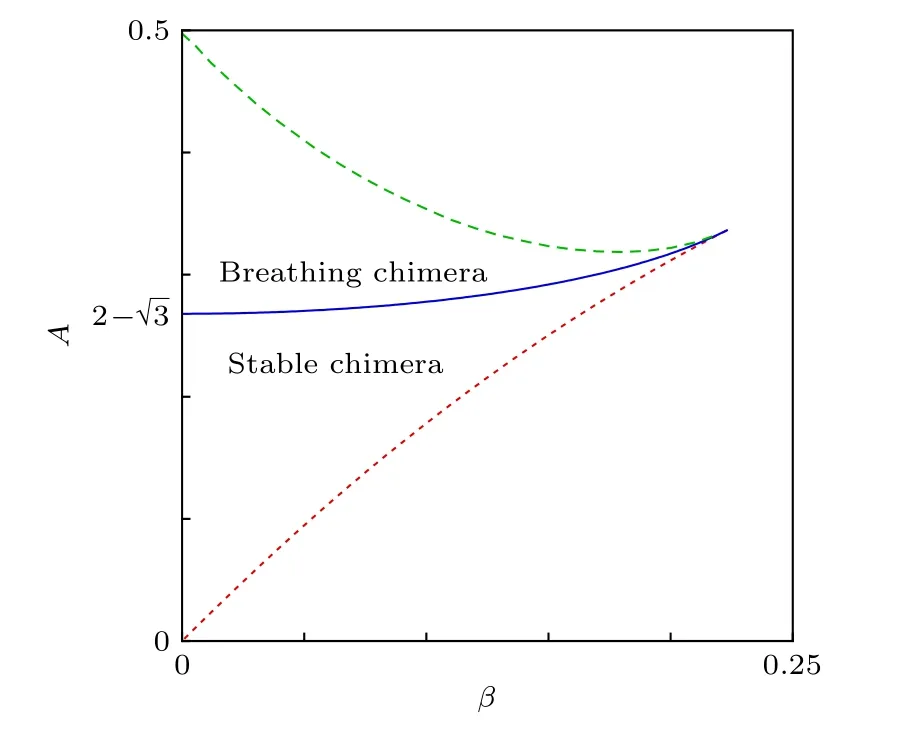
圖3 奇異態的穩定性相圖 分岔曲線: 鞍-節分岔(點劃線)、超臨界Hopf分岔(實線),兩者都是解析發現的;同宿分岔(虛線),數值發現的.改編自文獻[25]Fig.3.Stability diagram for chimera states.Bifurcation curves: saddle-node(dotted line)and supercritical Hopf(solid line),both found analytically;homoclinic(dashed line),found numerically.Figure adapted from Ref.[25].

當網絡結構不是全連網,而是二維或三維規則格子甚至復雜網絡時,奇異態會表現出多種多樣性,其斑圖豐富多彩[29-33].Zhu等[34]研究了復雜網絡情形,發現此時的斑圖會比較混亂,但如果按振子的有效頻率進行重新排序,則仍可見清晰的同步與無序共存.詳細的信息可見綜述文獻[10,11,35].

有鑒于此,為了定量刻畫奇異態,Kemeth等[36]于2016年引入了一個特征分類方法來測量奇異態.其基本思想是測量空間關聯,即對于具有局部或非局部耦合拓撲的系統,采用局部曲率來測量空間關聯.據此,一維系統時局域曲率可由二階導數測量,一維以上的系統則由拉普拉斯算子來完成.具體步驟如下.

i)對于包含空間數據 f 的每一個時間步或快照,我們用分立的拉普拉斯算子D來計算每個節點的局部曲率.以一維情形為例,對時間 t 時的快照,我們計算

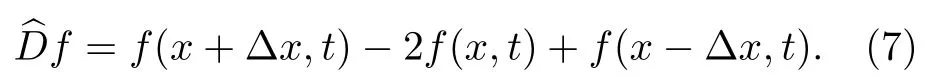
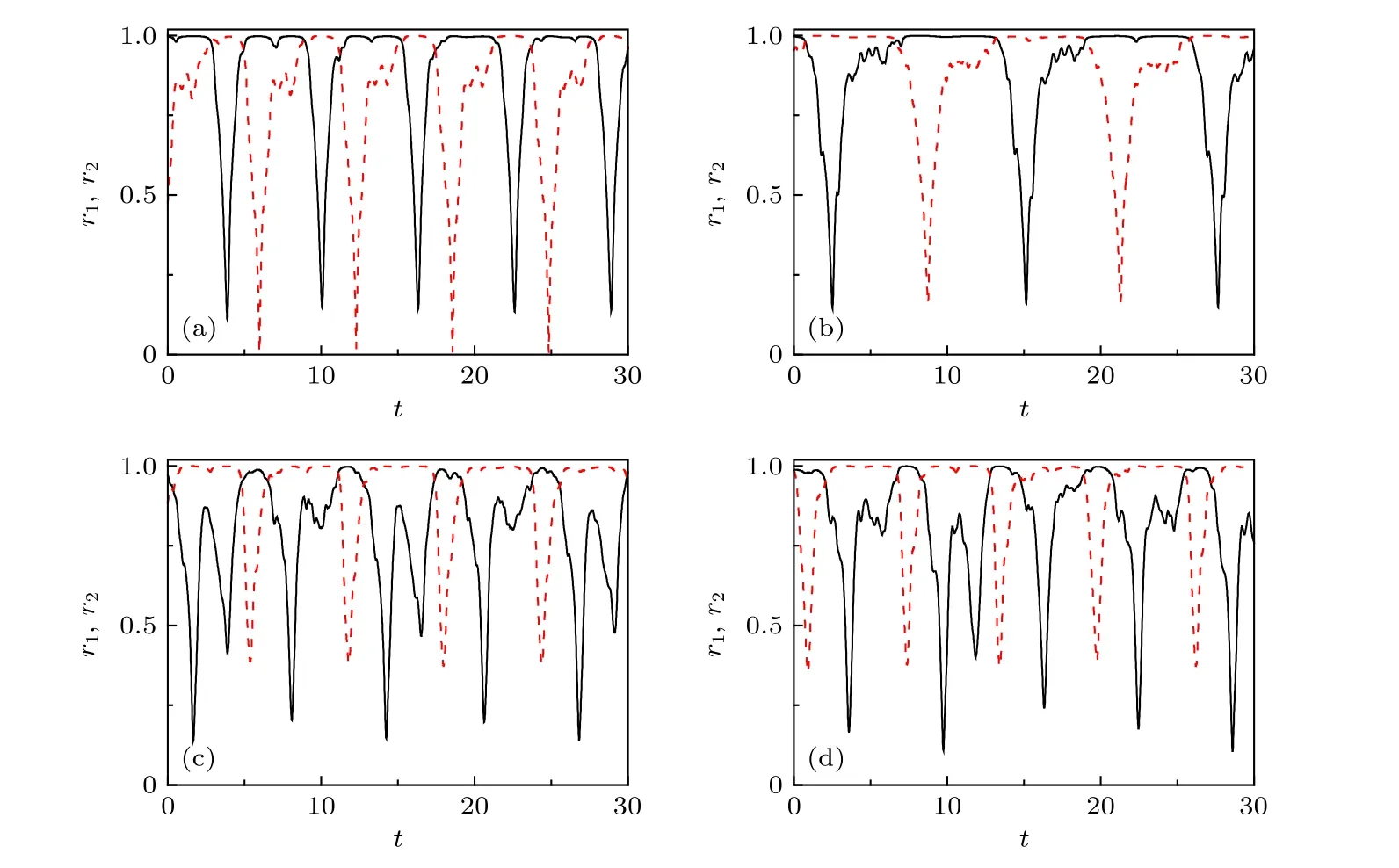
圖4 外部信號誘導的交替奇異態(a)A=1,Ω=1 與τ2=1.5;(b)A=1,Ω=0.5 與τ2=1.5;(c)A=1.5,Ω=1 與τ2=1.5;(d)A=1,Ω=1 與τ2=3.0 .改編自文獻[27]Fig.4.Alternating chimera states induced by external signals:(a)A=1,Ω=1 and τ2=1.5;(b)A=1,Ω=0.5 and τ2=1.5;(c)A=1.5,Ω=1 and τ2=1.5;(d)A=1,Ω=1 and τ2=3.0 .Figure adapted from Ref.[27].

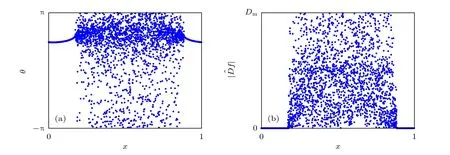
圖5 (a)來自于Kuramoto模型的快照;(b)將拉普拉斯算子用于(a)中的數據后得到的局部曲率的絕對值.改編自文獻[36]Fig.5.(a)Snapshot of the Kuramoto model;(b)absolute value of the local curvature obtained by applying the discrete Laplace operator on the data set shown in(a).Figure adapted from Ref.[36].

iii)考慮到數值模擬中的誤差漲落,Kemeth等[36]建議只要局部曲率的絕對值小于最大曲率的百分之一就應該被當作相關態,其他的為非相關態.為此,他們引入關聯測度

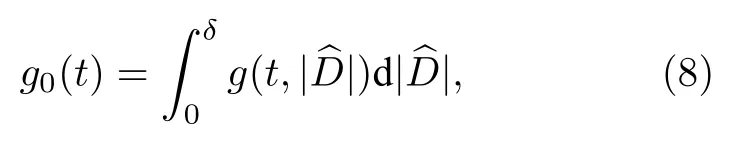
其中 δ=0.01Dm.實際計算中可用 g0(t)的時間平均值來衡量奇異態.

奇異態概念最直接的應用就是神經系統,特別是大腦網絡,目前這方面的研究很豐富[37-44].不同于一維的相振子模型,神經元系統通常由二維或三維模型來表示,此時的相互作用由耦合矩陣表示.研究中比較常用到的是FitzHugh-Nagumo(FHN)神經元模型.Omelchenko等[37]為FHN模型引入了一種旋轉耦合,并發現了多奇異態.他們將N個神經元放置在一個圓環上,每個神經元與其最近鄰的 2 R 個神經元發生耦合.其動力學方程如下:

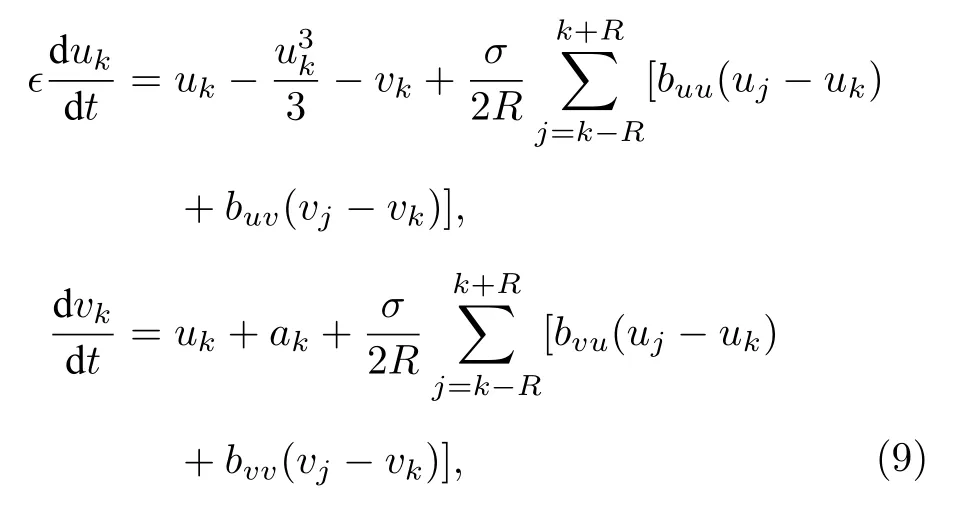
其中 uk與vk分 別表示快變量與慢變量,? 為一個小參數,這里取為0.05.依賴于閾值 ak,每個單獨的FHN振子顯示振蕩(| ak|＜ 1)或可激(| ak|＞ 1)行為,這里取 ak∈(-1,1).為簡單起見,他們將耦合取為旋轉矩陣

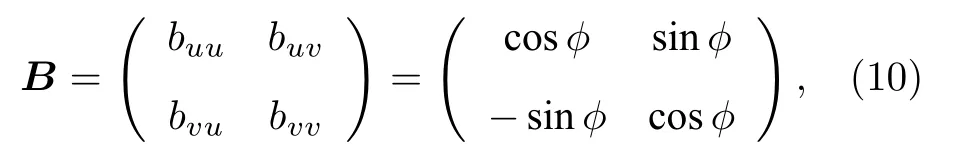
此耦合依賴于相參數 φ ∈ [-π,π] .

令 r=R/N,則參數r與σ就將決定系統的行為.圖6(a)—圖6(d)給出了參數r與σ分別取(0 .33,0.1),(0 .33,0.19),(0 .33,0.23)及(0 .33,0.28)時變量 uk的快照.為方便比較,同時給出了每個振子的平均相速度 ωk=2πMk/ΔT,其中 Mk為時間間隔 Δ T 內完成的圈數.常數 ωk代表鎖相區域.從圖6(a)—圖6(d)可見,隨著耦合強度σ的增加,奇異態從單一的非相關區域變成了兩個非相關區域,即觀察到了多奇異態[37].類似地,圖6(e)—圖6(h)給出了從單一的非相關區域變成三個非相關區域的情形.

在大腦網絡方面的應用主要是將網絡結構考慮成不同大小的真實腦皮層網[13,45-47],然后研究這些特定網絡結構下的奇異態.值得一提的是,Kang等[13]發現了對應“首晚效應”或半腦睡眠的奇異態.他們使用的腦皮層網絡數據含有998個節點、17865條邊[48,49],但其中含有9個孤立的沒有邊的節點.去掉這些孤立節點后,網絡只有989個節點,其中右半腦含有496個節點(i=1 —496)、左半腦含有493個節點(i=497 —989).考慮到左右半腦只能通過胼胝體連接,腦皮層網實際上是個雙層網絡,它的17865條邊可分成右半腦內的8037條邊、左半腦內的7773條邊以及連接左右半腦的2055條邊.

考慮到通過胼胝體的連邊與半腦內的連邊具有不同的信號傳播速度,Kang等[13]提出了一個雙層網模型(A,B 層)并讓層內與層間的耦合強度不同,分別由 λin與λout表示.A層的方程為

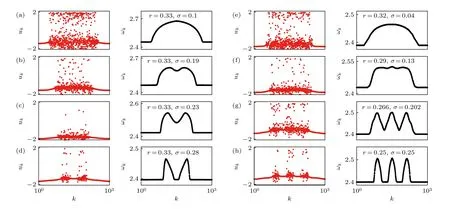
圖6 單一的非相關區域變成多個非相關區域的情形(a)—(d)變成兩個非相關區域:(e)—(h)變成三個非相關區域.在每個子圖中,左列代表變量 uk 的快照,右列為對應的平均相速度.改編自文獻[37]Fig.6.Transition from a classical chimera state with one incoherent domain to multichimera states with two(a)—(d),and three(e)—(h)incoherent domains.In each panel the left column shows snapshot of variables uk,and the right column shows the corresponding mean phase velocities.Figure adapted from Ref.[37].

這個雙層網模型可展示不同的狀態,包括同步化、無序及奇異態.圖7給出了四個典型的狀態,其中上層為網絡A、下層為網絡B、子圖為它們對應的動力學.非常有趣的是,圖7(c)與圖7(g)顯示出網絡A無序而網絡B同步,為典型的半腦睡眠現象,從而再現了“首晚效應”.

除了這些數值模擬與理論研究外,奇異態已被數個實驗證實[50-54].比如Martens等[52]簡單地使用了兩個擺座、一根彈簧和一些全同的節拍器實現了奇異態.隨著彈簧彈力系數的增大,一個擺座上的節拍器全同步,另一個擺座的節拍器會出現各種不同的非協同行為.該實驗無需精妙耦合計算和時間延遲,且能容易地拓展至其他物理模型.Gambuzza等[53]則使用電路實驗模擬了FHN模型的奇異態,發現了一種靜止態和同步態混合的奇異態.

3 遙同步

大量的證據表明,人腦的信息處理是分布式的,并由具有社區結構的復雜網絡承擔[55].一個腦區的信息可為其他腦區用來進行認知計算,這種跨過多個腦區的處理過程稱為信息的分散與整合[56].在這個分散與整合的過程中,有一種特殊的信息傳遞方式―遙同步,指不直接相連的兩個節點通過連接一個公共的鄰居而相互間發生同步,但卻不與那個公共鄰居同步[57].其證據是在采集的多電極大腦數據中,無論是 β 帶(14—30 Hz)還是 γ 帶(40—80 Hz)都有各腦區間神經活動的長程同步.由于這些遠距離腦區間軸向傳導延遲可達到幾十毫秒,這種遠距離的同步放電很可能是中繼振子介導的[58].事實上,中繼神經元廣泛存在于我們的神經系統中,比如丘腦、脊髓和外側膝狀體.例如,丘腦就負責視覺信號從視網膜到視覺皮質的轉播.目前,遙同步已在部分實驗中得到證實[59].

遙同步是Bergner等[57]在研究星形網的相同步時引入的.他們考慮的模型如下:

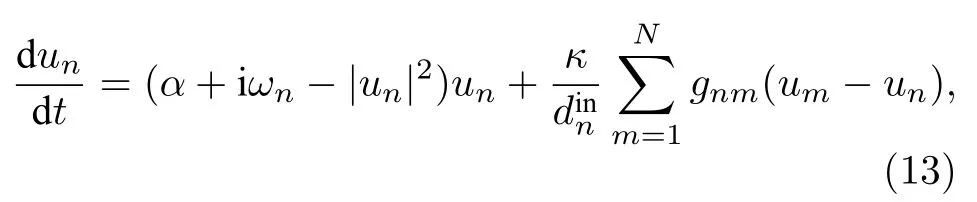
其中 un是復數,α 為霍普夫分岔參數,ωn為振子未耦合時的本征頻率,κ為耦合強度,為節點的入度,(gnm)為鄰接矩陣.圖8為他們研究遙同步時的星形網示意圖.

以 N=5 為例,Bergner等[57]取中心節點的頻率 ω1=2.5,4個葉子節點的頻率為{0.975,0.992,1.008,1.025},即中心節點的頻率遠大于葉子節點的頻率.令 un=xn+iyn,并引入相位 φn=tan-1(yn/xn),則可定義

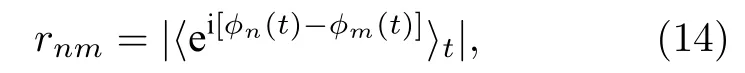
其中 〈 ·〉t代 表時間平均,rnm為節點n與m之間的局部序參量.為了檢驗遙同步,可引入兩個序參量.一個用來測量中心節點與葉子節點間的關聯

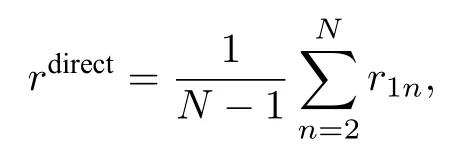
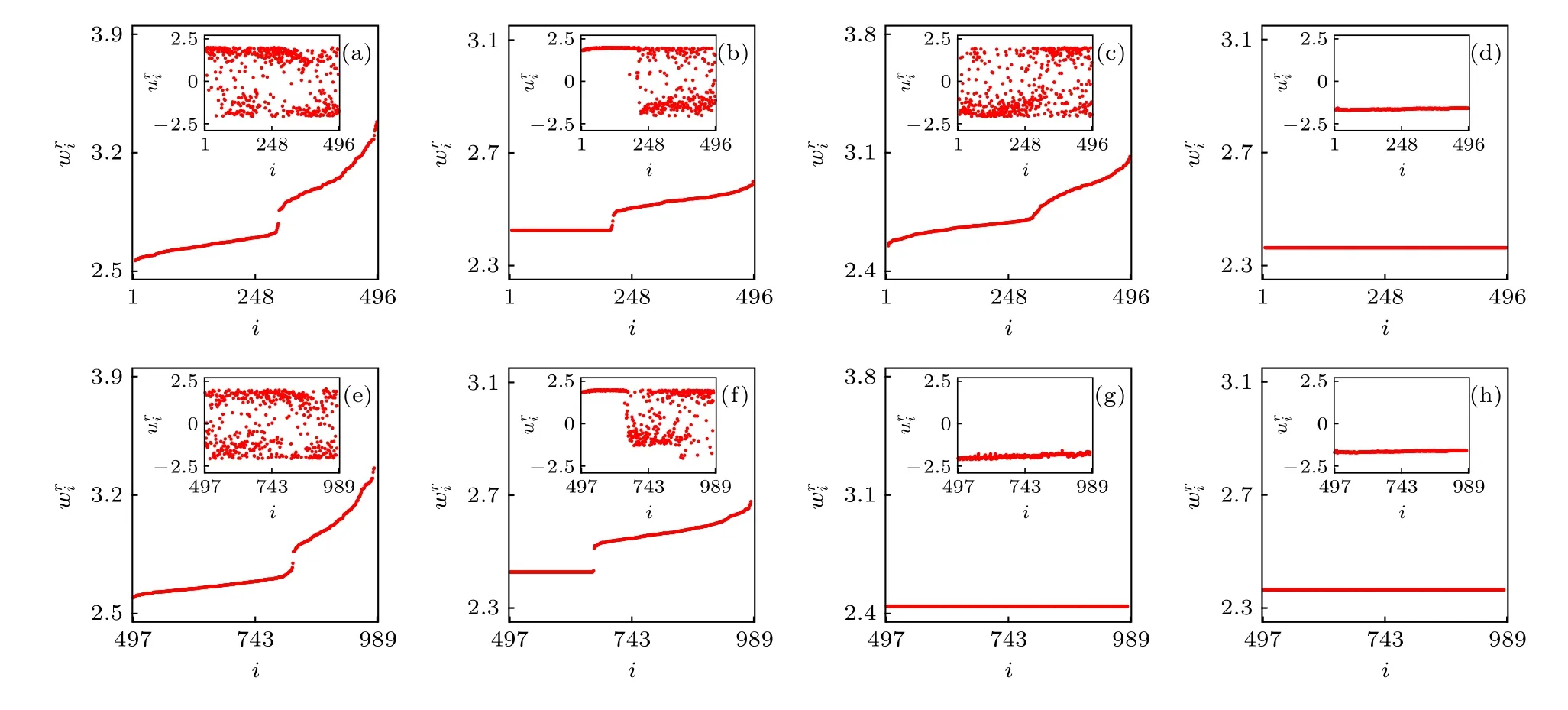
圖7 大腦皮層網中的四個典型的行為.參數為 α =π/2-0.1,上層為網絡A、下層為網絡B、子圖為它們對應的動力學ui(a)與(e)的耦合參數為(λin=0.1,λout=0.3);(b)與(f)的耦合參數為(λin=0.1,λout=1.8)、(c)與(g)的耦合參數為(λin=0.4,λout=3.5);(d)與(h)的耦合參數為(λin=4.0,λout=3.5).改編自文獻[13]Fig.7.Four typical behaviors in the cerebral cortex with α =π/2-0.1 where the up and down panels represent the two hemispheres,respectively,and the insets are their corresponding dynamics of ui at a moment t.The parameters are λin=0.1 and λout=0.3 in panels(a)and(e)of disorder;λin=0.1 and λout=1.8 in panels(b)and(f)of chimera state;λin=0.4 and λout=3.5 in panels(c)and(g)of an emergent state conceptually similar to the state of unihemispheric sleep;and λin=4.0 and λout=3.5in panels(d)and(h)of synchronization.Figure adapted from Ref.[13].

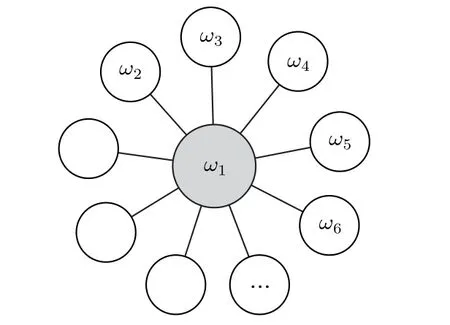
圖8 用于遙同步的星形網示意圖.改編自文獻[57]Fig.8.Graphic visualization of a hub network motif(star motif).Figure adapted from Ref.[57].

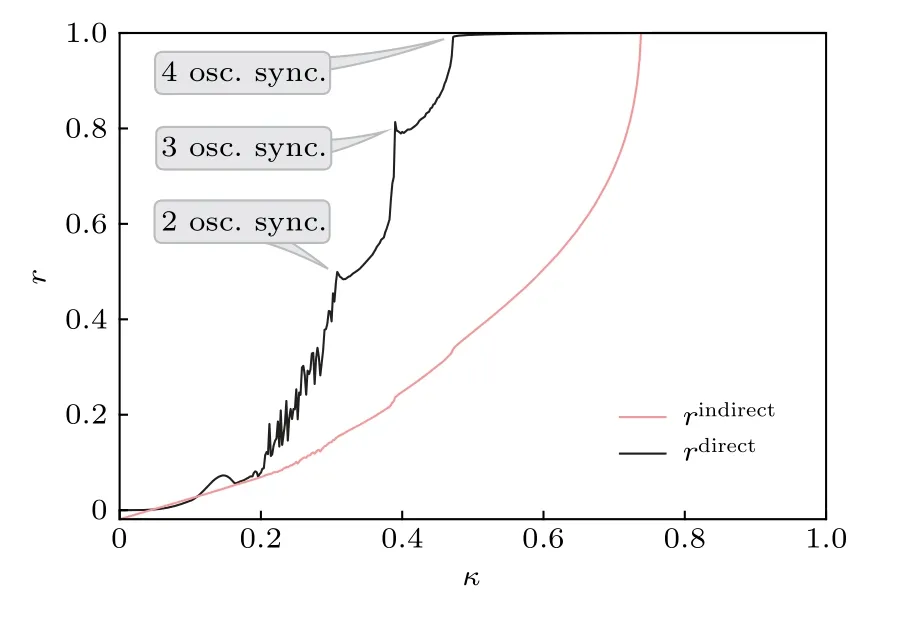
圖9 相同步的過程.相同步的建立清晰可見,其中的三個標注分別表明兩個、三個與四個葉子節點間的同步化.改編自文獻[57]Fig.9.Transition to PS for the hub motif.From the plot the onset of RS is clearly visible.The three annotations indicate synchronization between two,three,and four peripheral oscillators,respectively.Figure adapted from Ref.[57].

另一個則用來測量葉子節點間的關聯

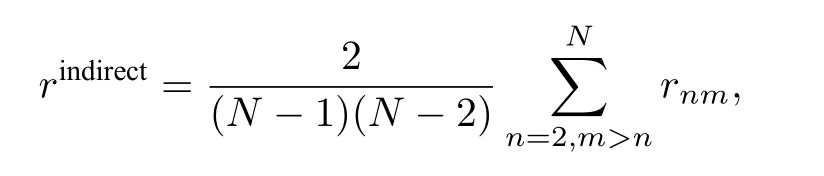
圖9給出了這兩個序參量對耦合強度κ的依賴性,可見葉子節點間關聯的增加要遠快于中心節點與葉子節點間的關聯.葉子節點在κ大約為0.47時達到完全相同步,而中心節點與葉子節點間的完全相同步要推遲到 κ ≈0.74 .

為了明白遙同步的機制,Bergner等[57]將模型進一步簡化為只有三個節點的情形: 兩個葉子節點1與2,由中心節點3間接連接.為了實現節點1與2的相互同步,節點1的活動需要傳遞給節點2,反之亦然.這就意味著節點3的動力學必須保證節點1與2的活動的傳遞盡可能不被改變,為此需要滿足兩個條件: 首先,為了不讓中心節點與葉子節點同步,節點3的吸引子的平均時間尺度應該與節點1與2的吸引子有很大的不同.此外,節點1與2的區別不應太大,以便它們能夠通過弱相互作用同步.其次,為了得到經過節點3的傳遞,節點3的擾動必須不能衰減得太快.將中心節點在其極限環(| u0|2=α)附近作線性化并保持其他兩個葉子節點非接觸,可得如下方程:

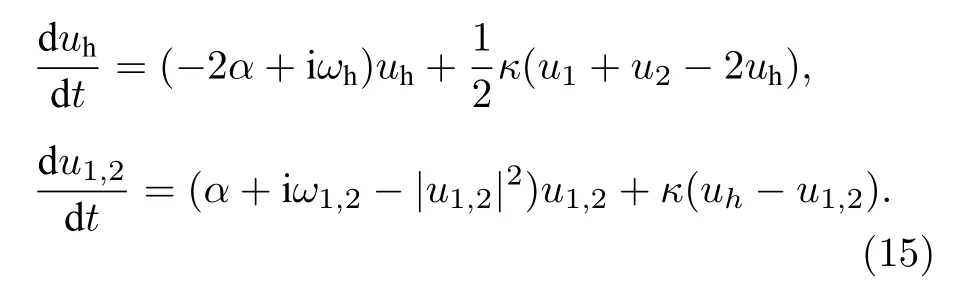
這是兩個Stuart-Landau振子通過一個線性過濾器耦合的方程.通過拉普拉斯變換可將這個過濾器的傳遞函數寫為

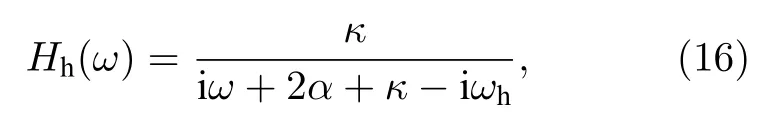
于是,中心節點可被一個有效耦合取代并有

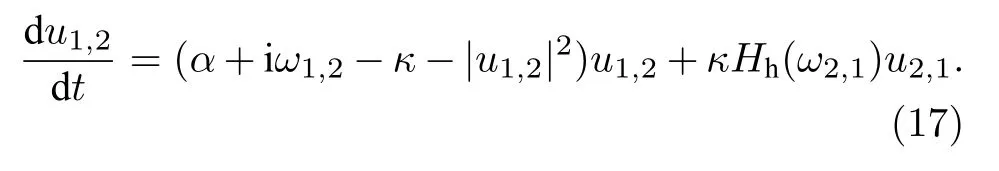
葉子節點實際上是對稱的,因此Nicosia等[60]研究了網絡對稱性對出現遙同步的影響.他們考慮的是帶相參數的全同的Kuramoto相振子,其相參數使得相連的振子保持特定的相差,從而阻礙完全同步.發現耦合網絡的對稱性起著重要作用,具有相同對稱性的兩個節點可以同步化,即使它們相距遙遠.這種遙同步是由網絡的對稱性導致的.Zhang等[61]則進一步研究了這種對稱性與遙同步的關系,將星形網的遙同步推廣到了網絡的情形,稱為非相干介導遠程同步.具體地,將N個節點組織成三組 A,B與C,其中A與B相連,B與C相連,但A與C不相連,見圖10所示.假定B組至少有兩個節點,且每個組內的節點與連邊形成一個相連的子網.他們發現那兩個非連續的A與C同步而中間B組與它們無關,且鏡像對稱性是這種遙同步發生的機制,比如A組中的節點1與C組中的節點N就具有鏡像對稱性而會完全同步.

基于大腦中的遙同步現象,Kang等[62]討論了第2節中那個真實腦皮層網絡上遙同步的可能性,發現對全同振子很難觀察到遙同步.但若考慮大腦中信號速度的有限而加進延遲時,遙同步則成為可能.具體地,考慮真實腦皮層網絡上每個節點為Stuart-Landau振子,滿足如下方程:

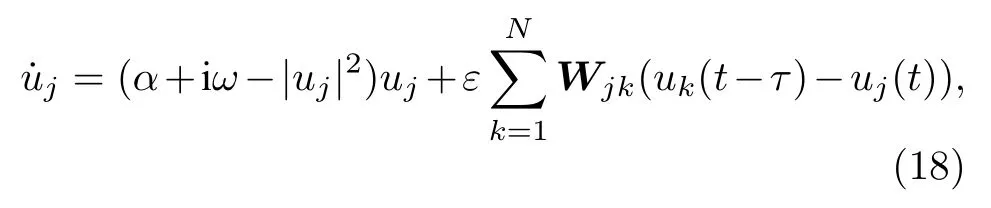
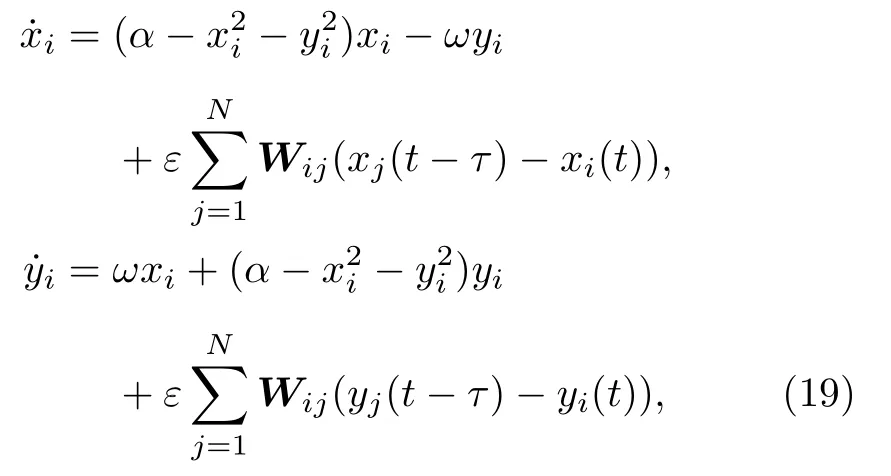
其中 xi與yi分別代表ui的實部與虛部.這里固定α=1.0 與ω=2.0.圖11給出了τ=0.5 與ε=0.1時的六個典型的遙同步斑圖,相似的斑圖也可在其他的參數τ與ε處發現.圖11的第二列與第三列清楚地表明每一個斑圖都有兩個或更多的中心節點,與第一列的斑圖只有一個中心節點形成了鮮明的對比.

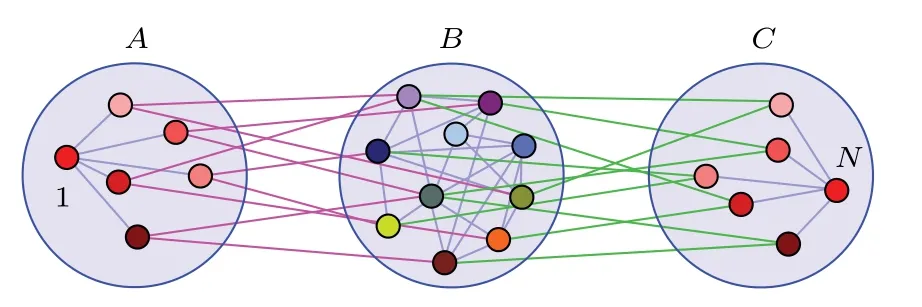
圖10 A與C組之間的遙同步同步由B組的介導來完成.節點的顏色代表了它們的狀態,可見節點1與N是完全同步的,而B組中節點的動力學是無關的.改編自文獻[61]Fig.10.Remote synchronization between node groups A and C mediated by incoherence in group B.The colors of the nodes schematically represent their states,indicating that nodes 1 and N are identically synchronized,while the dynamics of the nodes in B are incoherent.Figure adapted from Ref.[61].

圖11的發現也不同于文獻[57]中的遙同步斑圖,因此有必要進一步挖掘.圖11的第二列與第三列的一個公共特征是它們的兩個中心節點是由一些公共葉子節點相連的.由此,Kang等[62]提出了一個新的遙同步框架,見圖12,其中紅、藍、粉紅數字分別代表中心節點、葉子節點與公共葉子節點.這個模型揭示,當公共葉子節點的耦合強度較小時,只能形成單個中心節點的遙同步.但當公共葉子節點的耦合強度較大時,兩個遙同步集團可以合并成一個較大的遙同步集團,此時那兩個中心節點同步成為一個同步集團,而所有的葉子節點成為另一個同步集團.詳情見原文,這里不展開討論了.

此外,還有其他的一些關于遙同步的研究,比如Gambuzza等[63]研究了多層網上的遙同步,Punetha等[64]研究了二分網上帶時間延遲的遙同步,Leyva等[65]研究了多層對稱網絡上的遙同步等.

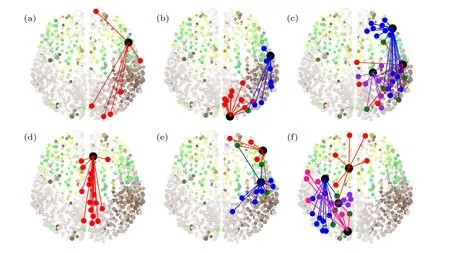
圖11 參數取 τ=0.5 與ε=0.1 時的六個典型的遙同步斑圖.每個斑圖都是按如下條件挑選的:(i)在中心節點與葉子節點間沒有同步化;(ii)所有的葉子節點均相互同步化.改編自文獻[62]Fig.11.Six typical patterns of RS for τ=0.5 and ε=0.1 .Each pattern is chosen by the conditions:(i)There is no synchronization between the hub and its peripheral nodes;(ii)all the peripheral nodes are synchronized each other.Figure adapted from Ref.[62].

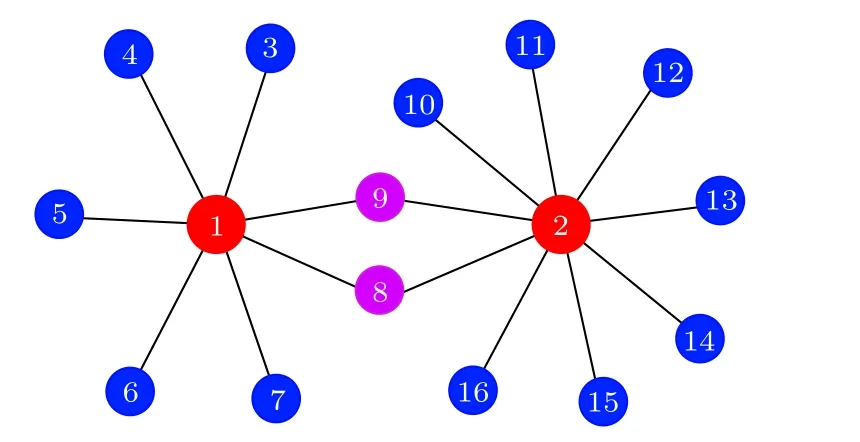
圖12 具有兩個中心節點的遙同步新框架示意圖,其中紅、藍、粉紅數字分別代表中心節點、葉子節點與公共葉子節點.改編自文獻[62]Fig.12.A schematic figure of the new framework of RS with two huns,where the nodes with red,blue and pink numbers represent the hub,leaf and common leaf nodes,respectively.Figure adapted from Ref.[62].

4 集團同步

集團同步表示網絡中特定集團內的振子將同步到相同的軌道而不同集團之間的行為則互不相同.這種同步集團可以出現在成群的動物中,其網絡為鄰居間的視覺連接,或者由局部通訊網連接的成群的無人駕駛汽車.集團同步也可以出現在電力網中,這將是出問題的征兆,即失去全局同步.最近的研究表明,網絡拓撲的對稱性與同步動力學集團的形成有重要關系[66-70],并已為較多的實驗證實[71-74],王新剛[70]對此有一個較全面的綜述.

為了說明耦合振子網絡中的對稱性與集團的概念,圖13(a)展示了一個四節點網絡,其中振子是全同的、耦合是雙向的[73].這個網絡總共有六個對稱.圖13(b)給出了圖13(a)中交換節點1與2的一個反射,網絡結構保持不變.圖13(c)展示了旋轉 1 200的網絡,其與原始結構(圖13(a))不可區分.這些對稱性可由鄰接矩陣A的對稱性來表示,其元素為 Aij=1 如果節點 i 與節點 j 相連,否則 Aij=0 .網絡的動力學可寫為

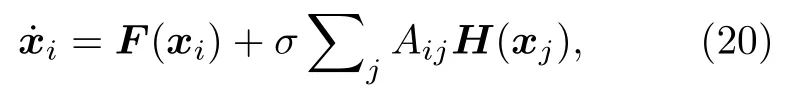
其中 i=1,···,N,xi為振子 i 的動力學矢量,F為振子的矢量場,H 為耦合函數.這個動力學方程也可寫成拉普拉斯耦合的形式

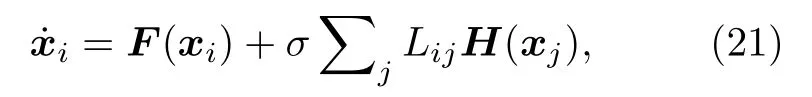
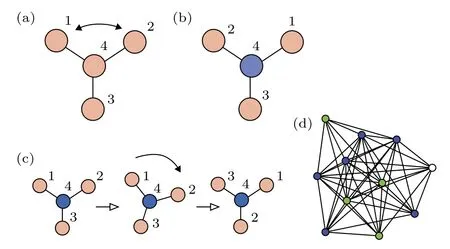
圖13 網絡中對稱性的例子(a)四個全同振子通過三根連線耦合的網絡;(b)一個反射操作后的同一網絡;(c)一個旋轉操作后的同一網絡;(d)一個 11 個節點的網絡有三個集團(藍、綠、白).改編自文獻[73]Fig.13.Examples of symmetries in networks:(a)A network of four identical oscillators coupled through three identical links;(b)the same network after a reflection operation;(c)the same network after a rotation operation;(d)an 11-node network showing three clusters(blue,green,and white).Figure adapted from Ref.[73].

在圖13(a)的網絡中,節點1,2與3有相同的運動方程,因此如果它們從相同的初始條件出發,就將能永久地保持同步化.節點4不能與任何其他節點置換且也不與它們同步,因此在圖13(b)與圖13(c)中將其標為不同的顏色.這是網絡中對稱性與動力學間的親密關系,它將網絡分成了兩個集團1,2,3與4.文獻[73]討論了對于給定的網絡,如何發現所有可能的集團同步斑圖.其主要結論是鄰接矩陣的對稱性對應動力學的對稱性,當它們從一個同步態出發,可置換的節點集構成的集團就將保持同步,即每個集團的同步態是動力學流不變的.圖14給出了所有允許的斑圖,其中屬于相同集團的節點標成了同一種顏色.

文獻[68]指出,基于集團的坐標變換可以更簡單且更快地計算網絡的對稱性.圖15是關于24個節點的網絡上的9個對稱性集團,其中每個集團中的節點具有相同的穩定性,而不同的集團則穩定性不同,且這些同步集團可唯一確定.此外,Dahms[66]等考慮了時間延遲對全同振子網絡上集體行為的影響,發現延遲耦合確實可以誘導出不同的同步集團,且允許集團同步的耦合矩陣在本征值譜上也顯示了非常類似的對稱性.

圖14 五個節點的網絡中的集團斑圖 左邊: 當網絡連接為鄰接矩陣(方程(20))時所有可能的斑圖;右邊: 當網絡連接為拉普拉斯矩陣(方程(21))時額外的斑圖.改編自文獻[73]Fig.14.Patterns of clusters in a five-node network.Left: All possible patterns displayed when the network connectivity is given by the adjacency matrix(Eq.(20));right: Additional patterns displayed when the network connectivity is given by the Laplacian matrix(Eq.(21)).Figure adapted from Ref.[73].

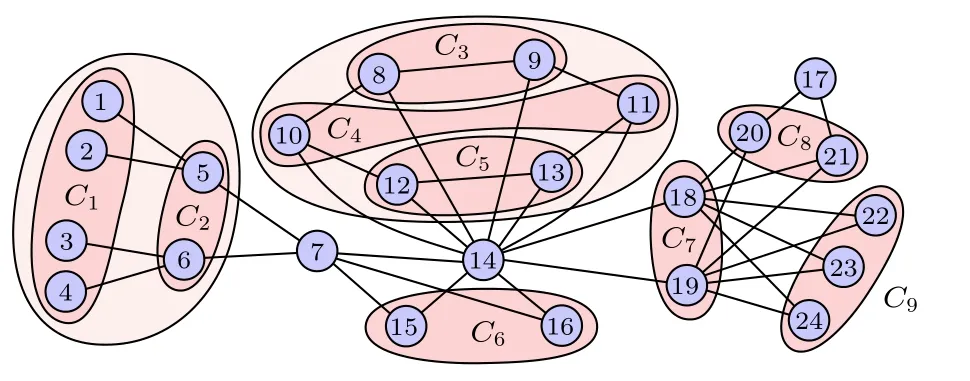
圖15 24個節點構成的網絡中對稱集團的分組.改編自文獻[68]Fig.15.Grouping of symmetry clusters in a CS pattern for a 24-node network.Figure adapted from Ref.[68].

5 討論與展望

至此,我們完成了對奇異態、遙同步與集團同步這三種部分同步態研究進展的介紹.從這些研究可見,它們三者之間既有聯系,也有區別.首先,它們三者都是介于完全同步與完全無序之間的中間態,承擔著從無序到同步的過渡任務.但這種中間態并不是通常那種大家逐漸靠近、序參量逐漸增大的二級相變過程,而是在位形空間中形成兩種性質截然不同的狀態且相互共存,這就比較神奇,從而成為了它的反直觀之處,同時也成就了它用于解釋大腦斑圖的特質.這個特質在奇異態中表現為相互連接的同步組與非同步組的共存,也可以是分開的多個同步組與非同步組的共存;在遙同步中表現為不直接相連的分散振子成為了同步態,而與它們相連的振子,尤其是中心節點,卻不與它們同步;在集團同步中表現為具有網絡對稱性的節點達成了同步,而不同對稱性的集團則成為不同的同步集團,同步的振子之間可以存在連接,也可以沒有直接的連接.這些不同的表觀形式其實可以看成是同一種現象的不同表述,就像量子力學中不同的表象一樣,供我們在不同的環境下有選擇地使用.

除了在表觀形式上不相同之外,它們三者出現的條件也不相同.奇異態最初要求的條件是非局域耦合,由衰減核描述.然后這個條件推廣為初始條件的不同,但非局域耦合的要求適當放寬,不再要求各個振子的耦合對象均有些不同,而改為各組內個體耦合的對象完全相同,但不同組間個體耦合的對象不相同.再然后進一步推廣為延遲系統,此時所有個體耦合的對象可以完全相同.遙同步主要討論的是朗道振子系統,本質原因是朗道振子可作為線性濾波器來傳遞不直接相連的節點間的耦合信息,從而使中心節點周圍的葉子節點達到同步.遙同步最初是在星形網上進行討論的,現已拓展至復雜網絡乃至真實的腦網絡.集團同步最初要求的是網絡位置完全對稱,這就導致對稱性相同的節點具有完全一樣的動力學方程,從而可達到完全同步的動力學行為.后來這個條件推廣為輸入量相同即可,因為所謂對稱性保證的實際上是耦合貢獻的等同.

事實上,這三種部分同步并不是完全獨立的,而是都可看成某種局部對稱性的體現.例如奇異態中同步組內的振子實際上具有相同的對稱性,遙同步中圍繞中心節點的葉子也具有完全對稱的地位,集團同步就更不用說了,它的定義就源自對稱性.按照這個局部對稱性的特點,我們其實可以拋開直接相連或不直接相連的具體細節,而將這三者統稱為局部同步態的涌現.在這個意義上,就不難理解在某些系統中可以同時出現多種部分同步態.比如圖11中的遙同步振子與其他的非同步振子一起就構成了奇異態,圖12中的遙同步振子因結構對稱也可當作集團同步.同理,對于圖15中的那些同步集團中的振子,如果它們不直接相連的話,就是遙同步了,比如 C2中的振子5與6.這種同時具有多個屬性的部分同步在大腦皮層網絡中非常普遍,或者說大腦皮層網就是一個典型的呈現各種各樣部分同步的系統.

這三種部分同步態的研究意義就在于它們可以被很好地用來解釋大腦高級功能的物理機制,包括感知、學習與記憶等.現在已經知道大腦神經網絡具有典型的復雜網絡特征,包括度分布的異質性、小世界特征及社團結構等.正是由于這些特征,才保證了大腦認知活動期間廣泛的斑圖,從而保障了大腦高級功能的實施.當大腦接收到不同的信號或刺激時,相應的動力學斑圖就會被啟動,或者實現從一個斑圖到另一個的轉換.具體表現就是我們觀察到的對應奇異態的首晚效應、對應遙同步的分布式計算及對應集團同步的斑圖多樣性等.

雖然這三種部分同步的研究取得了不錯的結果,在大腦機制的闡述方面也取得了重要的進展,但對大腦及大腦運行機制的研究依然是個長期而艱巨的任務,還有許多開放的問題等著我們進一步研究.下面是根據我們自己的研究經驗建議的幾個開放問題.

1)如何將這三種部分同步得到的現有結論充分地用于探索大腦功能的機制,比如認知、記憶與信號傳播等方面.

2)現有研究大多局限于單層網絡.由于大腦的社區結構特征,多層復雜網絡上的部分同步更值得期待.文獻[13]是這樣的一個例子,但更進一步、更深入的探討還很缺乏.

3)如何能跳開結構層面的分析,從更深的層面來揭示出一些更本質的東西,比如從本征值譜分析的角度來進行分析等.這方面的一個先期探索是關于本征模與模塊化結構間的內在聯系[75].

4)如何根據這三種部分同步的特征來控制各種神經疾病如帕金森氏病、癲癇、阿爾茨海默病、精神分裂癥與腦腫瘤等.

5)除了這三種典型的部分同步外,是否還存在其他的部分同步態或者根本就不能歸結為部分同步但卻是腦功能所必須的狀態? 如果有的話,如何去揭示它們?

我們期待部分同步化的研究在大腦神經元網絡的機制與應用方面發揮越來越重要的作用.希望本綜述起到拋針引線的作用,激勵出更多、更好的工作.