基于時延補償的AUV領航跟隨編隊控制

馮之文，姚 堯，苗 艷，馮景祥

(江蘇自動化研究所，江蘇 連云港 222006)

0 引 言

在過去的幾十年中，自主水下航行器(AUV)已被廣泛用于執行各種水下任務，包括民用和軍事應用，如深海檢查、海洋測繪。對于某些特定應用，例如海洋采樣、測繪和海底測量，通過多個AUV合作執行任務可以提高效率、增大服務區域并在發生故障時提供冗余，提高了系統的穩定性。一般來說，有3種主要類型的編隊控制策略：即基于行為的策略[1-2]，虛擬結構策略[3-4]，和領導者-跟隨者編隊策略[5]。每種策略都有自己的優點和缺點[6]。在這些策略中，領導者-跟隨者編隊策略由于其簡單性和可擴展性等優點而被許多研究廣泛考慮。

在多AUV編隊系統中，AUV的通信能力有限以及環境的限制，水聲通信受到傳播速度的限制，不可避免地會產生較大的時延;水聲通信具有高噪聲、多途干擾、多普勒傳播等不穩定特性，使通信具有較高的誤碼率;水聲通信所消耗的能量遠高于陸上無線通信，造成水聲通信范圍遠遠變小。這類弱通信系統的主要特征有:不可忽略的通信時延、間歇性通信失效或中斷、有限通信范圍以及高誤碼率等。

信息延遲是弱通信系統必須面對的問題，對系統穩定性的影響不能忽視。由于接收到的領航AUV信息存在時間上的滯后性，系統在未來時刻的狀態由當前狀態和歷史狀態共同決定，系統的穩定性受到時延大小的影響。當個體間的信息傳輸延遲太大，超過某一臨界值時，多AUV系統無法形成穩定的編隊隊形，使原來穩定的編隊變為不穩定。文獻[7]中，作者基于一致性的思想研究了水聲通信帶來的通信延遲問題，提出的控制律能夠允許一定的通信時延，達到了編隊控制的目的。文獻[8]中，作者提出了具有通信約束的分布式水下航行器群編隊控制算法，當航行器間的通信時延小于某個確定的上界時，算法是有效的。但是文中每個個體接收到的鄰居個體的信息狀態及其時間導數均存在一個固定的時延T，現實中個體與個體之間的通信時延是時變的，算法上具有一定的局限性。文獻[9]中，作者針對時延問題，提出了一種不同時變通信延遲的解決方法，也是將AUV的編隊時延問題轉化成一致性問題。

目前，國內外雖然對編隊控制的研究策略取得了一定的成果，有部分學者對此類問題展開了研究，但都是在較為理想的條件下展開研究，比如時延不變而且已知，或者時延可變但有時延上限，且大部分研究主要是進行一致性的算法設計，基于一些比較簡單的模型得到一致性收斂的條件。基于以上的分析，針對通信延遲下，領航跟隨編隊控制方法隊形穩定性變差的問題，本文提出了一種基于時延補償的編隊控制方案，采用反步法和李雅普諾夫直接法設計了領航跟隨編隊控制律，實現了理想通信情況下的編隊保持。接著引入通信時延，利用最小二乘法根據領航AUV的當前和歷史狀態信息進行狀態的擬合，根據時延誤差預測出當前時刻的領航AUV的狀態信息，帶入到控制器中進行擬合。從仿真結果可以看出，該方法簡單有效，可以減小編隊的誤差，提高編隊的穩定性。

1 問題描述

1.1 AUV數學模型

本文只考慮AUV二維平面內的運動，因此只考慮AUV水平面內的數學模型，可分為運動學模型和動力學模型，分別如下：

(1)

(2)

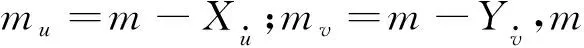
從式(2)中可以看到，對于側向速度vr而言，是沒有任何外部輸入的。

1.2 AUV領航跟隨編隊描述

考慮由n個AUV組成的系統，這些AUV將保持所需的編隊隊形，并且每個跟隨AUV都可以和領航AUV組成1個子系統。對于每一個子系統，當領導者AUV巡航時，可以生成跟隨者的參考軌跡，以使其跟隨位置ηf相對于領導者位置ηl的距離為ρ，方向為α。我們提出了針對每個跟隨者AUV的跟隨編隊控制算法。令ηl=[xl,yl,ψl]T，表示為領航者的位置矢量。然后，領導者的運動學模型可以描述為：

(3)

式中：vl=[ul,vl,rl]T，為領航者AUV的速度矢量。

類似地，跟隨者AUV的運動學模型可以描述為：

(4)

如圖1所示，跟隨者AUV的期望位置和領航者AUV的幾何關系如圖1所示。

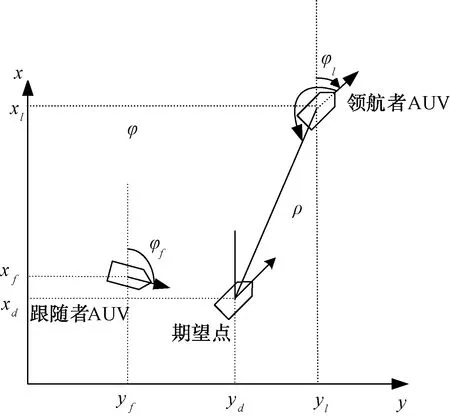
圖1 領航跟隨方法示意圖

由此幾何關系可以用領航者AUV的位置信息矢量表示跟隨者AUV的期望位置矢量信息如下：

(5)

只要控制跟隨船跟蹤并沿著參考船軌跡運動，便可以實現編隊航行。因此，基于領航-跟隨方法的編隊控制問題可以描述如下：在可以獲知領導船的位置、姿態信息的條件下，為跟隨船設計控制律，使得xf→xd,yf→yd,ψf→ψl。

1.3 控制律的設計

在這里首先假設領航者AUV與跟隨者AUV之間的通信是理想的，即領航者AUV與跟隨者AUV之間的通信不存在延時，在理想通信的情況下進行控制律的設計[10]。

(1) 運動學控制律的設計

由于AUV是欠驅動的，因此在其橫向上沒有控制輸入。因此首先要設計控制速度uf和rf。定義跟隨者AUV與參考船的絕對誤差：

(6)

式中：ψd?Atan2(-ey,-ex)，并定義d?‖[ex,ey]T‖2，提出以下速度控制律，以使d和eψ收斂為零。

(7)

(8)

式中：ku,kr>0。

證明：應用上述控制律，誤差動態描述可以寫為：

(9)

又cosψd=ex/d,sinψd=ey/d，所以d和eψ對時間的導數可以寫成：

(10)

eψ收斂到0的證明：

(11)

(12)

因此，可以容易地得出結論：eψ有界并收斂到零，即eψ是漸近穩定的。

d和vf的有界性：

-(d22/m22)vf-(m11/m22)×

{[-vf(taneψ-eψ/coseψ)-

kud/coseψ-al(·)-bl(·)taneψ]·

(13)

為了簡化計算，對式(13)進行化簡，在這里定義：

(14)

取李雅普諾夫函數為：

(15)

其導數為：

[g2(·)+eψ]dvf+g3(·)vf

(16)

根據楊氏不等式定理可以得出下列不等式：

(17)

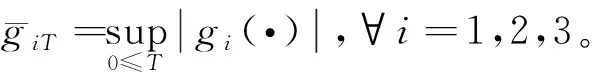
所以可以得到：

(18)

(19)

(20)

因此可以得出結論：對于所有的t∈[t0,T]，vf,d都是一致有界的。現在考慮t∈[T,∞)的情況，根據eψ收斂到0的證明，隨著T→∞，eψ收斂到0，然后，通過選擇足夠大的T和足夠小的正常數ε,a,b，可以得出以下不等式：

(21)

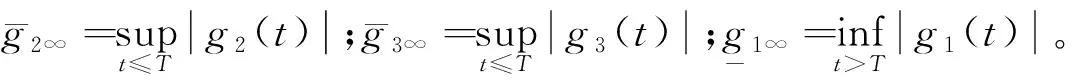
然后，利用楊氏不等式，可以得出：

(22)

式(22)證明，對于t∈[T,∞)，vf和d都是有界的，結合之前證明的對于所有的t∈[t0,T]，vf,d有界，所以對于?t≥t0，Vf和d是一致有界的。d的收斂性證明參照文獻[11]的級聯理論進行證明，不再進行贅述。

(2) 動力學控制律的設計

為了對動力學控制律進行設計，本文借助反演法將控制律擴展到動力學的層面上，將式(7)中的uf和rf作為虛擬的控制輸入ufd和rfd。

首先引入誤差變量：

(23)

式中：ufd和rfd為所需的速度控制輸入。

速度誤差的時間導數可推導為：

(24)

考慮由式(10)和式(24)描述的系統，應用以下動力學控制律：

(25)

式中：kτ1，kτ2為正數。

動力學控制律穩定性證明：

取李雅普諾夫函數：

(26)

其導數為：

(27)

根據楊氏不等式，可以獲得以下不等式：

(28)

然后，如果選擇速度控制增益，使得ku,kr>γ/2，則閉環系統漸近穩定。

2 基于時延補償的編隊控制

2.1 AUV通信方式

水下通信環境比陸地上要差得多，為了提高通信的穩定性，目前的AUV領航跟隨編隊一般選取領航AUV廣播自身狀態信息的方式，將信息傳遞給跟隨AUV。如圖2所示，設#1為領航者AUV，#2～#n為跟隨者AUV，領航者AUV將自身的狀態信息廣播給跟隨者AUV，跟隨者AUV與領航者AUV、跟隨者AUV與跟隨者AUV之間均不進行通信。

圖2 AUV群體通信方式

領航者AUV廣播的狀態信息為(x,y,ψl,t),x,y為領航者AUV的位置信息，ψl為領航者的航向角信息，t為發送信息時的時間，即時間戳，當通信理想時，按照1.3節所設計的控制律編隊就可以得到很好的保持，即：

(29)

但在實際應用當中，AUV之間的通信并不能被理想化，通信延時是必然存在的，領航者在t時刻廣播的狀態信息必然不能在t時刻被跟隨者AUV所接收，對于不同的跟隨者，存在著不同的通信時延τi，即跟隨者AUV會在t+τi時刻接收到領航者AUV在t時刻廣播的狀態信息，此時若不進行補償，則跟隨者的控制律變為：

(30)

延時系統框圖如圖3所示。

圖3 通信延時下的領航跟隨編隊控制系統框圖

在此控制律下，隊形的保持必然不如理想通信條件下的編隊效果，因為控制律中的狀態信息永遠不是當前時刻的領航者的狀態信息，因此，需要對當前的情況采取一定的措施來改善通信延時對編隊隊形的影響。

2.2 AUV通信補償原理

在實際問題中，人們常常需要從1組觀測數據(xi,yi)，i=1,2,…,n中作出一種預測：下一個x對應的y值是什么，即預測函數y=f(x)的表達式。從幾何上看，這個問題就是要由給定的數據點(xi,yi)，i=1,2,…,n去描繪曲線y=f(x)的圖像，即所謂的數據擬合問題。插值方法可以作為處理這種問題的一種數值方法，但不是很好的方法。因為現在所給數據本身就不一定可靠，而插值曲線要求嚴格通過所給的每一個數據點，這種限制會保留所給數據的誤差。此外，所給數據的數量通常很多，也會影響插值的效果。曲線擬合方法就是希望從這一大堆看上去雜亂無章的數據中找出規律來，設法構造一條所謂的擬合曲線，反映所給數據點總的趨勢，最小二乘法就是這樣的一種擬合方法。

由于AUV的機動性能不強，本文將基于最小二乘法提出補償時延的方法。最小二乘法是很經典的參數估計方法，它計算快速簡單，通常用多項式擬合模型去逼近目標軌跡，通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小。

領航AUV廣播的自身狀態信息中包含(x,y,ψl,t)，假設領航AUV在tm時刻廣播了自身的狀態，系統中的某個跟隨AUV在tn時刻接收到了領航者AUV在tm時刻(在這里，AUV自身信息傳播時間忽略不計)的信息，則該跟隨者AUV可以計算出時延τ，假設跟隨者AUV在tn時刻之前一共接收到n個領航者AUV的狀態信息，分別記為(x1,y1,ψl1,t1),(x2,y2,ψl2,t2),(x3,y3,ψl3,t3)...(xn,yn,ψln,tn)，本文的任務是根據這些歷史信息盡可能去預測領航者AUV在tm時刻的狀態信息(xm,ym,ψlm,tm)以及tm和下一通信時刻的中間狀態信息。

本文中的領航者狀態信息是一個四維數組時間序列，無法直接應用最小二乘法預測領航AUV當前時刻的狀態，因此需要對過去時刻的狀態信息進行相應的處理，本文將狀態信息(xi,yi,ψli,ti)轉化成3個二維狀態(xi,ti),(yi,ti),(ψli,ti)，然后運用最小二乘法對歷史時刻的數據進行擬合，可以得到3條關于自變量t的曲線方程如下：

(31)

根據擬合好的曲線對tm時刻的狀態信息進行求解，將t=tm代入求解，得到xm,ym,ψlm，最終得到領航者經過時延補償以后的狀態量(xm,ym,ψlm,tm)，在下一個領航者狀態信息到來之前，都將根據擬合好的狀態曲線對領航者的狀態信息進行預測，整個過程如圖4所示。

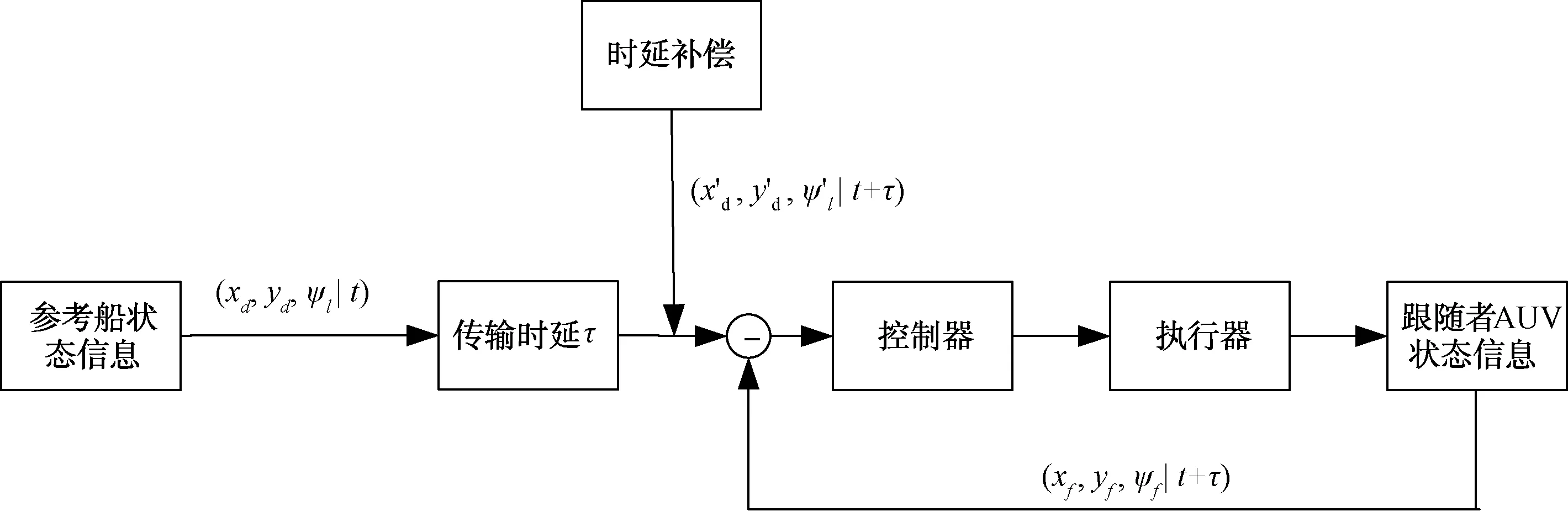
圖4 通信延時補償下的領航跟隨編隊控制系統框圖

2.3 算法流程

一般來說，曲線的擬合要用到過去時刻的大量AUV狀態信息，但考慮到AUV在水中的機動性較差，也就是說AUV的運動趨勢是緩慢變化的，因此在補償通信延時，對領航者AUV的狀態進行預測的時候，無需將過去時刻的所有狀態信息考慮在內，只需要選取當前時刻之前的k組狀態信息來擬合領航者AUV的運動狀態，隨著跟隨AUV不斷接收領航者廣播的狀態信息，跟隨者AUV不斷滑動采集當前時刻以及當前時刻之前的狀態信息，實現了對領航者AUV運動軌跡的動態更新，這種做法可以提高補償的快速性。

具體算法如下：

(1) 領航者AUV按周期向跟隨AUV廣播自身的狀態信息；

(2) 跟隨者AUV根據接收到的領航者AUV的狀態信息計算出時延τ；

(3) 確定領航者AUV的前k個狀態信息，根據最小二乘法對公式(31)進行擬合；

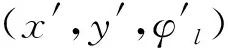
(5) 將預測得到的狀態信息代入到設計好的控制器式(30)當中,得到下一時刻的狀態量；

(6) 到達領航者AUV廣播周期，返回(1)。

3 仿真實驗

(1) 理想通信情況下的AUV領航跟隨控制

由圖5可以看出，在通信理想且連續的情況下，3個AUV在本文所設計的控制律中達到了較好的編隊效果，圖6和圖7表明了領航者AUV和跟隨者AUV之間的距離和相對方位角達到了仿真時所設置的期望值，驗證了控制律的有效性。

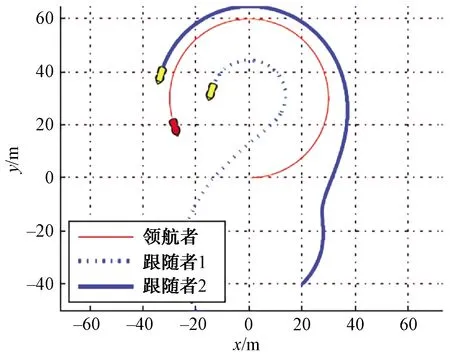
圖5 理想通信下AUV領航跟隨編隊路徑圖

圖6 理想通信下領航跟隨AUV之間的距離

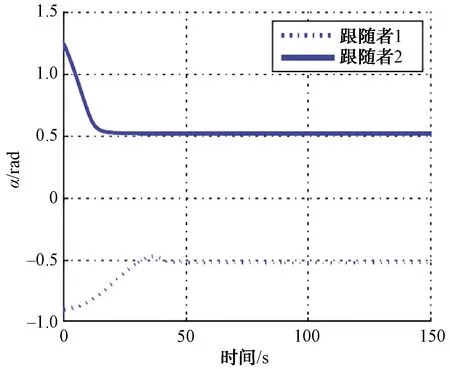
圖7 理想通信下領航跟隨AUV之間的相對方位角

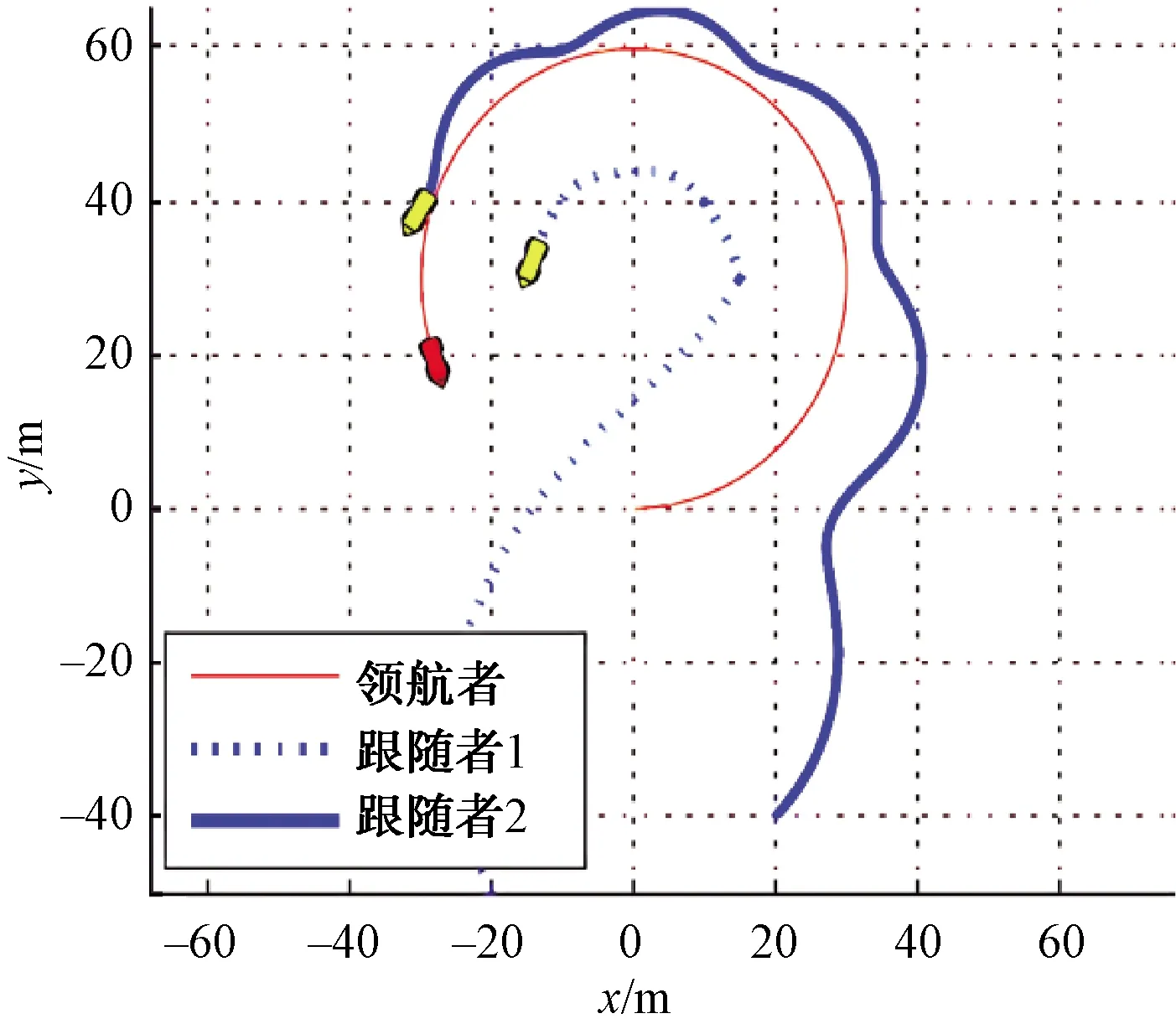
圖8 通信延時下領航跟隨AUV路徑圖

(2) 通信延遲下的領航跟隨AUV編隊控制

圖8顯示了通信延時下的領航跟隨編隊，由于通信延時和通信間隔的存在，相比于理想通信條件下，編隊效果較差。根據圖9可以看出，由于通信時延和通信間隔的存在，每隔10 s控制律才會做1次相應的調整，跟隨者AUV與領航者AUV之間的相對距離已經不能維持在本文所設置的理想距離，并且領航者所做的是圓周運動，所以跟隨者AUV與領航者AUV之間的距離在20 m上下浮動。由圖10可以看出，跟隨者AUV與領航者AUV的相對方位角也因為延時和通信間隔的存在無法達到較好的跟蹤效果。

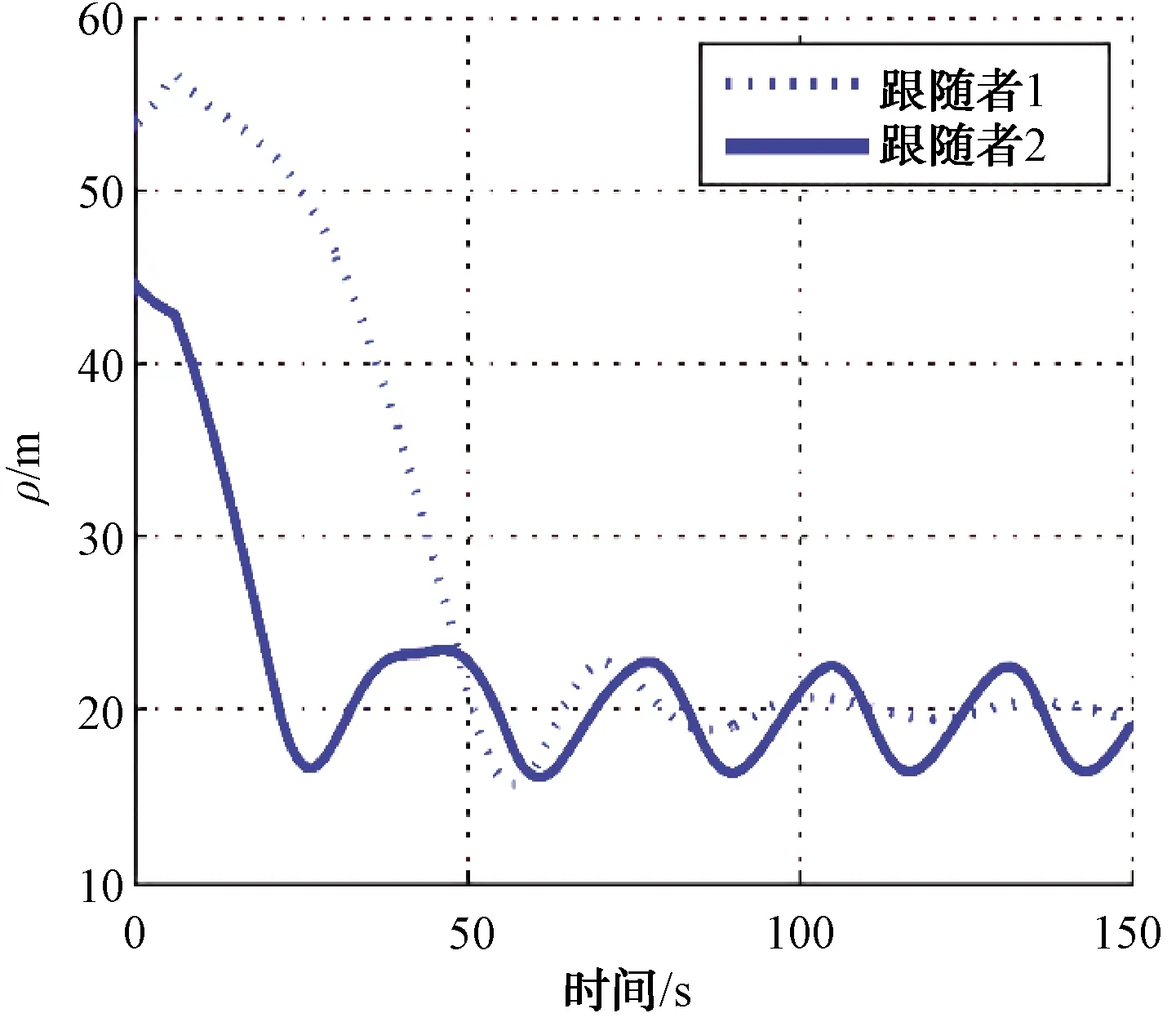
圖9 通信延時下領航跟隨AUV之間的距離

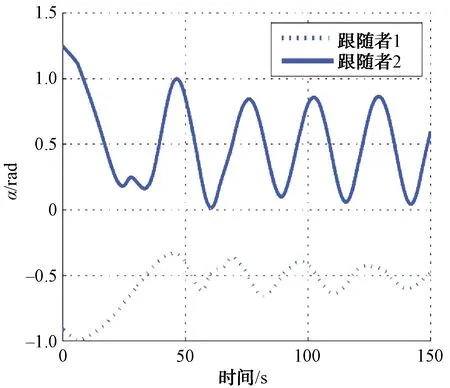
圖10 通信延時下領航跟隨AUV的相對方位角

(3) 時延補償下的AUV編隊控制

圖11顯示了通信延時情況下引入延時補償和預測的編隊效果，和理想通信條件相比，收斂速度略微有點差距但相比于通信延時情況，隊形得到了很大的改善。從圖12和圖13可以看出，領航者AUV與跟隨者AUV到了我們所期望的距離和方位角，達到了很好的跟蹤效果。

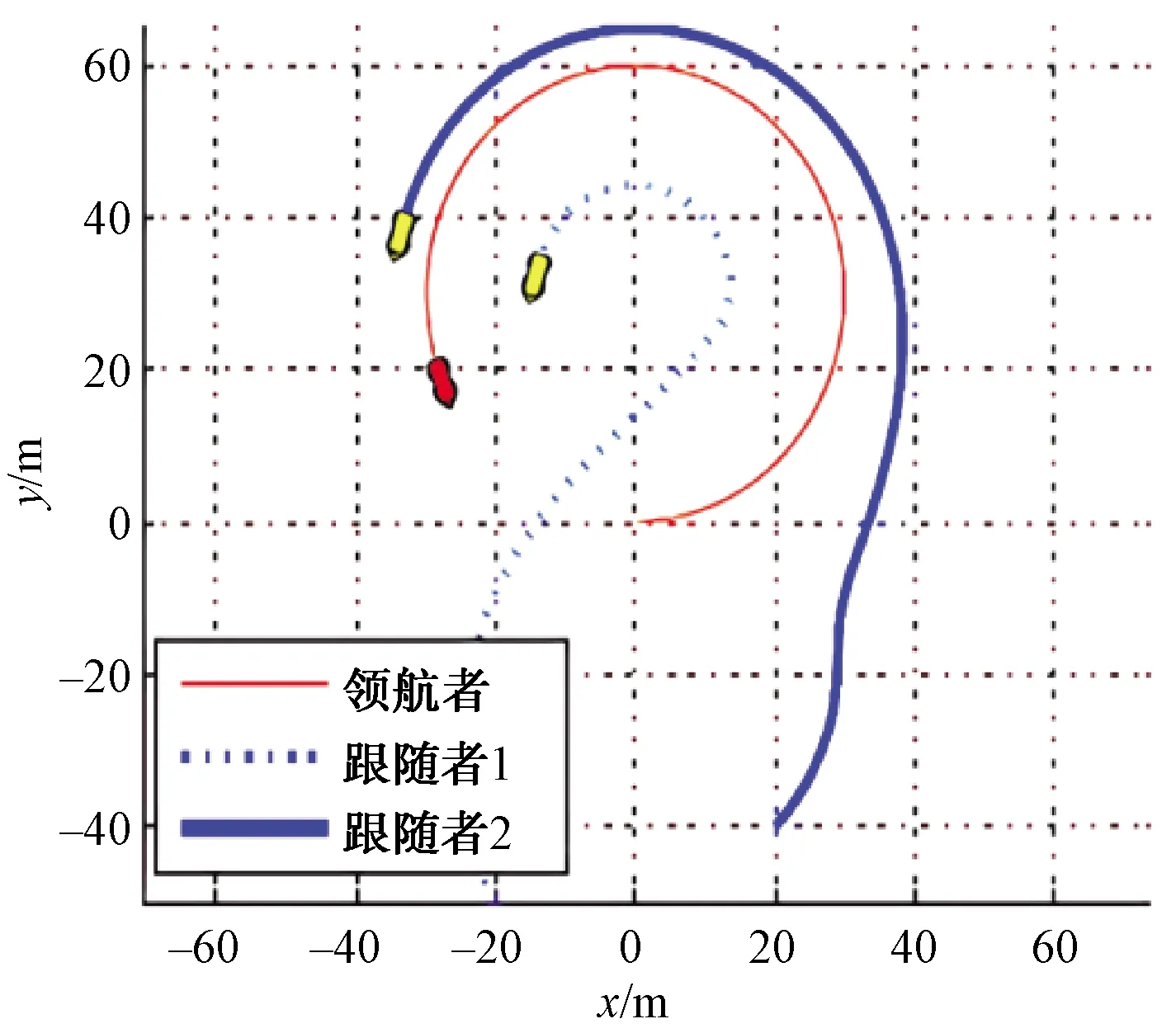
圖11 時延補償下領航跟隨AUV路徑圖

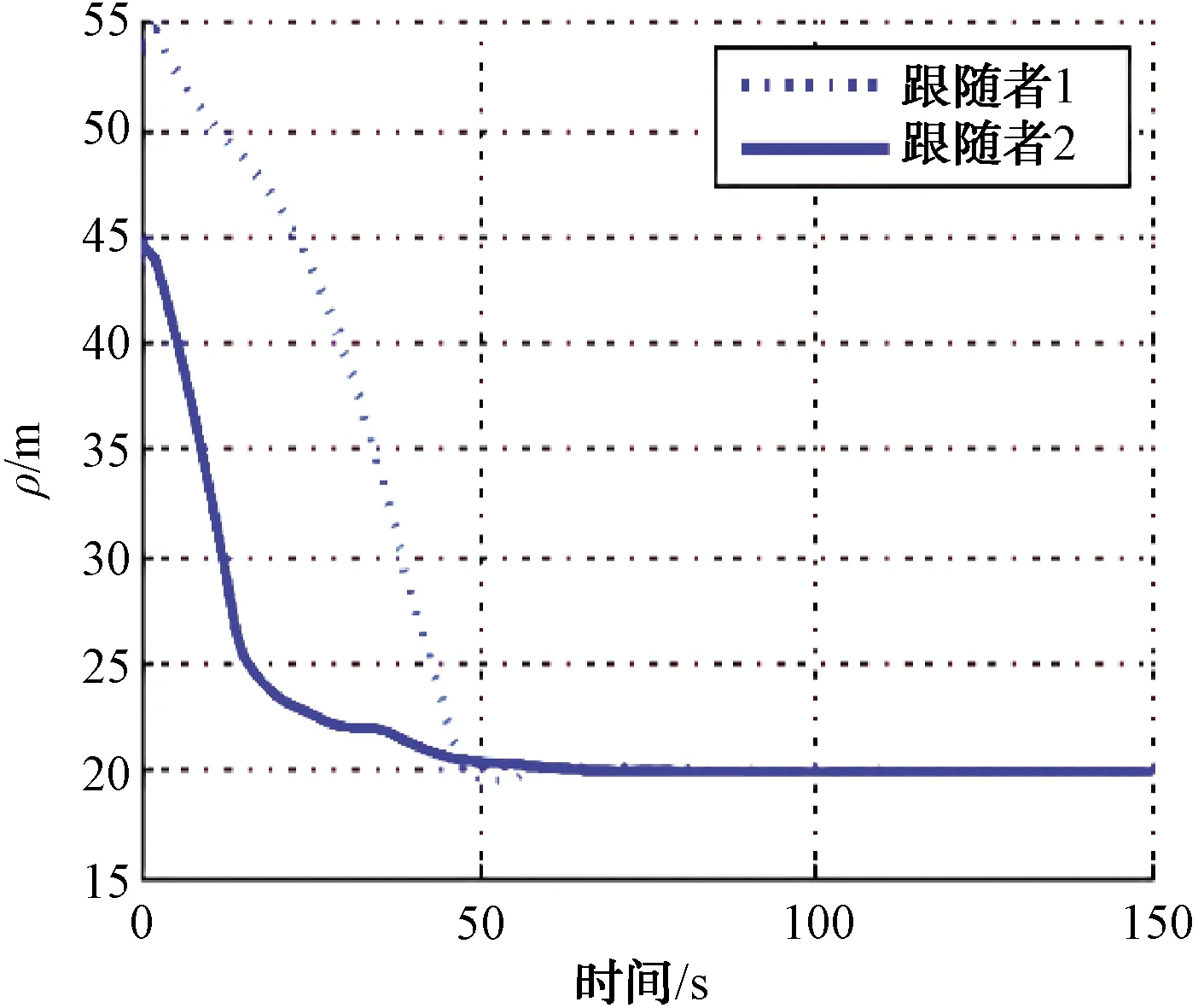
圖12 時延補償下領航跟隨AUV之間的距離

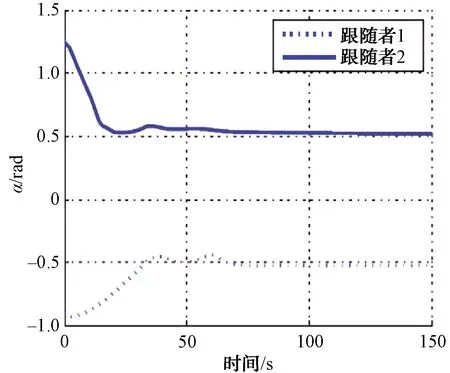
圖13 時延下領航跟隨AUV之間的相對方位角

4 結束語

本文對AUV領航跟隨編隊控制中的通信延時問題提出了一種延時補償的方法，領航AUV將自身狀態傳遞給跟隨AUV，跟隨AUV根據領航AUV發送的當前狀態信息與歷史狀態信息進行預測，并根據時延的大小預測出領航AUV當前時刻的狀態信息，用于補償領航跟隨AUV之間的通信延時，減小系統的編隊誤差。通過仿真可以看出本文所提方法的有效性，減小了編隊誤差并提高了編隊穩定性。但本文在設計的過程中，沒有考慮到控制器的約束問題，結合控制約束問題進行延時補償將是下一步工作。