基于循環譜和ELM-LRF的調制識別算法

李 晨，楊俊安，劉 輝

(國防科技大學，安徽 合肥 230037)

0 引 言

調制識別是指在不了解接收信號的情況下，確定其調制類型的一種技術手段[1]。它在軍事通信和民用通信領域都有廣泛的應用，例如認知無線電、頻譜監視和電子戰系統[2-4]。傳統的調制識別算法可以分為兩大類[5]：基于決策理論的方法和基于統計模式識別的方法。決策論方法基于概率論和假設檢驗原理[6]，計算量大且難處理。相比之下基于統計模式識別的方法比較簡單，它首先提取調制信號的調制特征，然后使用特定的分類器完成識別。由于決策論方法的突出缺陷以及機器學習相關理論發展如火如荼，現有的調制識別算法大多數是基于模式識別的方法。然而，模式識別方法的性能絕大程度上取決于所提取的人工特征，這些人工特征是研究者根據經驗以及大量實驗所得出來的，不一定是最佳的，因此需要尋求一種通過機器自動尋找和提取最優特征的方法。

近年來，深度學習在圖像識別領域中取得了廣泛的應用[7-9]，它從圖像中自動提取特征，在訓練樣本充足的條件下能獲得很高的識別率。由于深度學習不需要提取人工特征，有越來越多的學者將其引入調制識別的研究當中[10-15]，文獻[11]提出了一種基于循環譜圖和深度稀疏濾波卷積神經網絡(AN-SF-CNN)的調制識別算法，對7種調制信號進行識別,在0 dB時識別率大于90%，但是這種方法存在訓練樣本量過大、訓練時間長的問題，實用性較差。文獻[12]提出了一種基于一維相位特征和卷積神經網絡(CNN)的調制識別算法，在0 dB下識別率能達到99%，這種算法的缺點是只能識別相移鍵控(PSK)信號和正交幅度調制(QAM)信號，需要人工提取特征作為CNN輸入，且同樣存在訓練樣本多和訓練時間長的問題。研究表明，深度學習方法具有很高的識別性能，能夠挖掘出調制信號的內在特性，但是缺點也很明顯，模型復雜、參數眾多、數據量大、訓練時間長等問題亟待解決。2015年黃廣斌等在極限學習機的基礎上受CNN思想的啟發，提出了基于局部感受野的極限學習機。它僅有一個隱含層(包含一個卷積層和一個池化層)，模型參數和訓練時間均較CNN大大減小[16]，分類精度也很高。

受到局部感受野的極限學習機(ELM-LRF)訓練速度快的啟發，本文提出了一種基于循環譜和ELM-LRF的調制識別算法，下面分別從循環譜理論、ELM-LRF原理、算法過程設計和實驗分析進行介紹。

1 循環譜的基礎理論

首先，假設有一個帶寬為fx的調制信號x(t)，它的自相關函數是一個隨時間變化的周期函數：

Rx(t,τ)=Rx(t+T0,τ)

(1)

式中：T0為一個符號的持續時間。

則自相關函數的傅里葉級數展開如下：

(2)

(3)

式中：α為信號x(t)的循環頻率；傅里葉系數RF,x(α,τ)稱為循環自相關函數，它可以進一步表示為：

(4)

這里需要注意的是，RF,x(α,τ)具有時間τ和循環頻率α2個參數。從公式(4)中可以發現，當α=0時，有：

RF,x(0,τ)=Rx(t,τ)

(5)

此時循環自相關函數變成了信號的自相關函數。可以發現，RF,x(α,τ)在本質上是x(t)x*(t-τ)做傅里葉級數展開時的系數。一個循環平穩信號存在零循環頻率和非零循環頻率，它的零循環頻率部分僅表現出信號的平穩性，只有非零循環頻率部分表征出信號的循環平穩特性。

對公式(4)做時間τ的傅里葉變化，然后得到了循環譜密度函數：

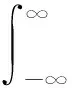
(6)

為了獲得循環譜密度SF,x(α,f)，國內外學者提出了許多循環譜估計的方法，常用的循環譜估計方法有基于時域平滑的方法和基于頻域平滑的方法，本文中采用的方法為快速傅里葉變換(FFT)累加法(FAM)，它是一種基于快速傅里葉變換的時域平滑方法。

2 超限學習機理論

2.1 經典超限學習機

超限學習機于2004年由黃廣斌等人提出[17]，它的網絡結構如圖1所示。

圖1 ELM網絡結構

由圖1可知，ELM的網絡結構與傳統的單隱層前饋神經網絡(SLFNs)一樣，它包括輸入層、隱含層和輸出層3層。因此，隱含層的輸出函數為：

(7)

式中：β=[β1,β2,…,βL]T，為輸出層到隱層的權值向量；h(x)=[h1(x),h2(x),…,hL(x)]T，為輸入樣本x在隱層的輸出向量。

事實上，h(x)將輸入數據從d維的輸入空間映射到L維的隱層特征空間。ELM的訓練過程實際上是最小化訓練誤差和輸出權重的范數：

(8)

式中：C為一個調整經驗風險和結構風險的尺度參數；T為訓練樣本的標簽；H為隱含層的輸出權值，可以表示為：

(9)

2.2 基于局部感受野的超限學習機

前面介紹了ELM的基本原理，相比于傳統神經網絡需要通過不斷迭代來調整權值，ELM不需要進行迭代，顯著提高了前饋型神經網絡的訓練速度。然而，傳統的ELM是在單隱層前饋神經網絡的基礎上提出來的，它是一種模仿人腦神經元信息傳遞過程的全連接結構，但是生物學研究表明，人的神經元還可以通過局部連接來傳遞信息。黃廣斌等人在文獻[16]中指出，雖然傳統ELM在很多應用方面都具有良好的泛化性能，但是涉及到圖像處理和語音識別等具有局部相關性的問題時，ELM由于僅具有全連接結構而不足以解決這些復雜問題。因此他受到卷積神經網絡的啟發，引入了局部連接的思想，提出了一種基于局部感受野的超限學習機，它的輸入層和隱層之間是通過連續概率分布連接的，因此具有局部連接的能力。相比于僅具有全連接結構的傳統ELM，包含了局部連接結構的ELM-LRF更為合理。

根據文獻[16]中關于ELM-LRF的介紹，可以得出它的網絡結構主要由4層組成：輸入層，隱含層(又可以稱為特征層)，組合層和輸出層。ELM-LRF的結構如圖2所示。

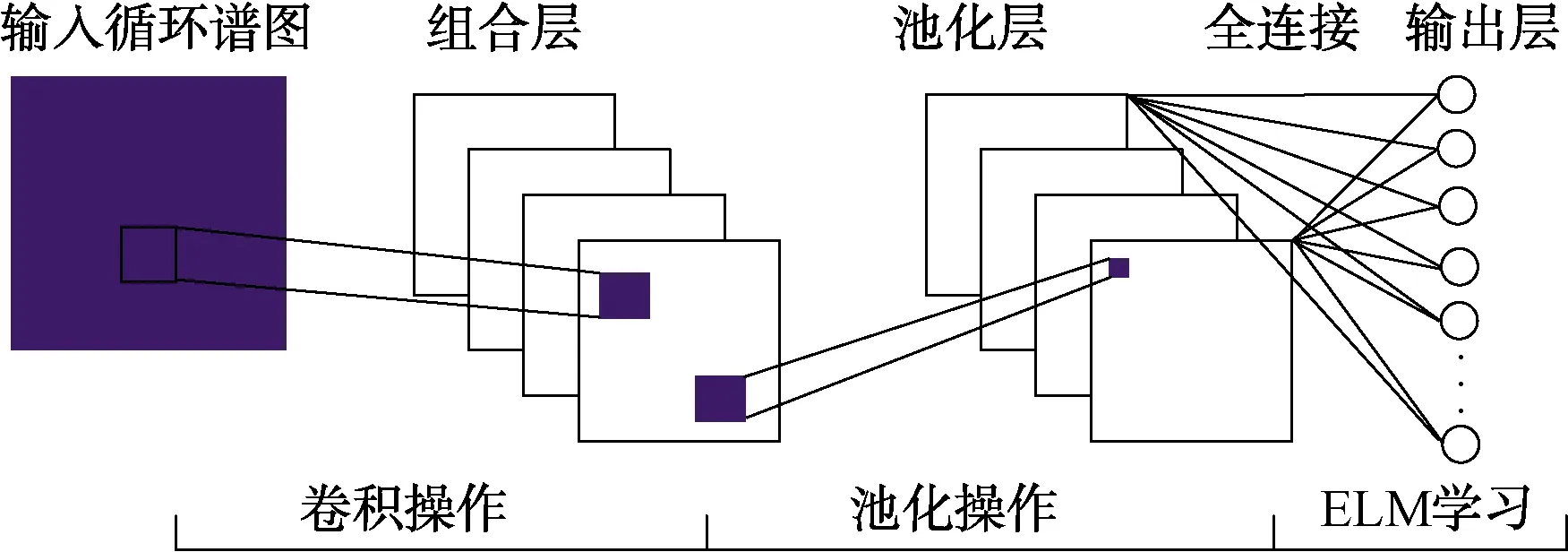
圖2 ELM-LRF網絡結構圖

下面根據以上網絡結構圖，按照從輸出到輸入的順序介紹ELM-LRF算法的機理和實現過程。

(1) 輸入層到隱含層

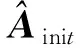
i,j=1,…,(d-r+1)

(10)

(2) 特征層到組合層

ELM中可以用多個節點或者節點構成的子網絡來表示一個節點，通常稱之為組合節點，因此不同的節點里面可能會包含部分相同的特征，這使得ELM-LRF網絡具有了平移和旋轉不變性，它的優點是增強了網絡學習局部特征能力。這種組合節點的方式其實就是一種池化過程，因此，組合層又可以稱為池化層。這里采用平方根池化的方法，從圖中可以發現，池化圖和特征圖具有一樣的尺寸，大小都為(d-r+1)×(d-r+1)，且他們的數量都為K個。這里采用hp,q,k表示第k個池化圖中的節點(p,q)的取值：

(11)

式中：p,q=1,2,…,(d-r+1)。

此時需要注意的是，在腳標i和j小于零的情況下，令Ci,j,k=0。

(3) 組合層到輸出層

由圖2可知，組合層到輸出層是一個全連接的結構，此時的輸出權值可以通過傳統的ELM訓練得到，即采用正則化最小二乘法的方法。假設有N個輸入圖像的訓練樣本，可以得到組合層的輸出矩陣H∈RN×K×(d-r+1)2，則β的計算公式為：

(12)

3 算法設計過程

本文提出的基于循環譜圖和ELM-LRF的調制識別算法屬于模式識別方法，整個識別過程如圖3所示。

圖3 識別流程圖

首先需對輸入數據進行歸一化處理，然后提取11種調制信號的循環譜。這里需要對循環譜進行歸一化處理并將數據集劃分為訓練集和測試集。接著是ELM-LRF網絡的訓練過程，傳統的基于模式識別的調制識別算法需要提取人工特征，而本文所用網絡是基于深度學習的思想，可以自動從數據中提取特征，代替了人工提取特征的過程，因而自動化程度更高。在訓練好網絡之后，用測試集進行測試，得到識別結果。

4 實驗結果與分析

4.1 數據參數設置

本文對11種調制信號進行識別，包括二進制振幅鍵控(2ASK)、四進制振幅鍵控(4ASK)、二進制頻移鍵控(2FSK)、四進制頻移鍵控(4FSK)、二進制相移鍵控(2PSK)、四進制相移鍵控(4PSK)、十六進制正交調幅(16QAM)、三十二進制正交調幅(32QAM)、調幅(AM)、調頻(FM)、調相(PM)。其中，調制信號的參數設置為：載波頻率fc=2 kHz,采樣頻率fs=20 kHz，數字信號符號速率為RS=1 250 B，信號長度為L=2 048。調制信號的信噪比從-2 dB到16 dB。將生成的數據集分為訓練集和測試集，每隔一個信噪比，訓練集有5 500個樣本，測試集有1 100個樣本。因此，每種調制類型的信號在每2個信噪比間隔下共生成600個樣本。

4.2 仿真實驗

在每個信噪比下進行了100次仿真實驗，對實驗結果取平均后，得到了每個調制信號的平均識別率如表1所示，算法的總體識別率如圖4所示。對表1分析可以發現，當信噪比低于0 dB時，2ASK，4ASK和32QAM的識別率最差，2FSK，4FSK和FM的識別率最好，均能準確識別出來。隨著信噪比的提升，識別效果逐漸改善，在4 dB時，除了2ASK和4ASK，大部分調制信號的識別率都得到了改善。由圖4可知，隨著信噪比的提升，算法的總體識別率也不斷提高，當信噪比大于4 dB時，算法的平均識別率超過了96%，說明ELM-LRF網絡從循環譜中自動學習出的特征是有效的，實驗結果驗證了本文算法的有效性。

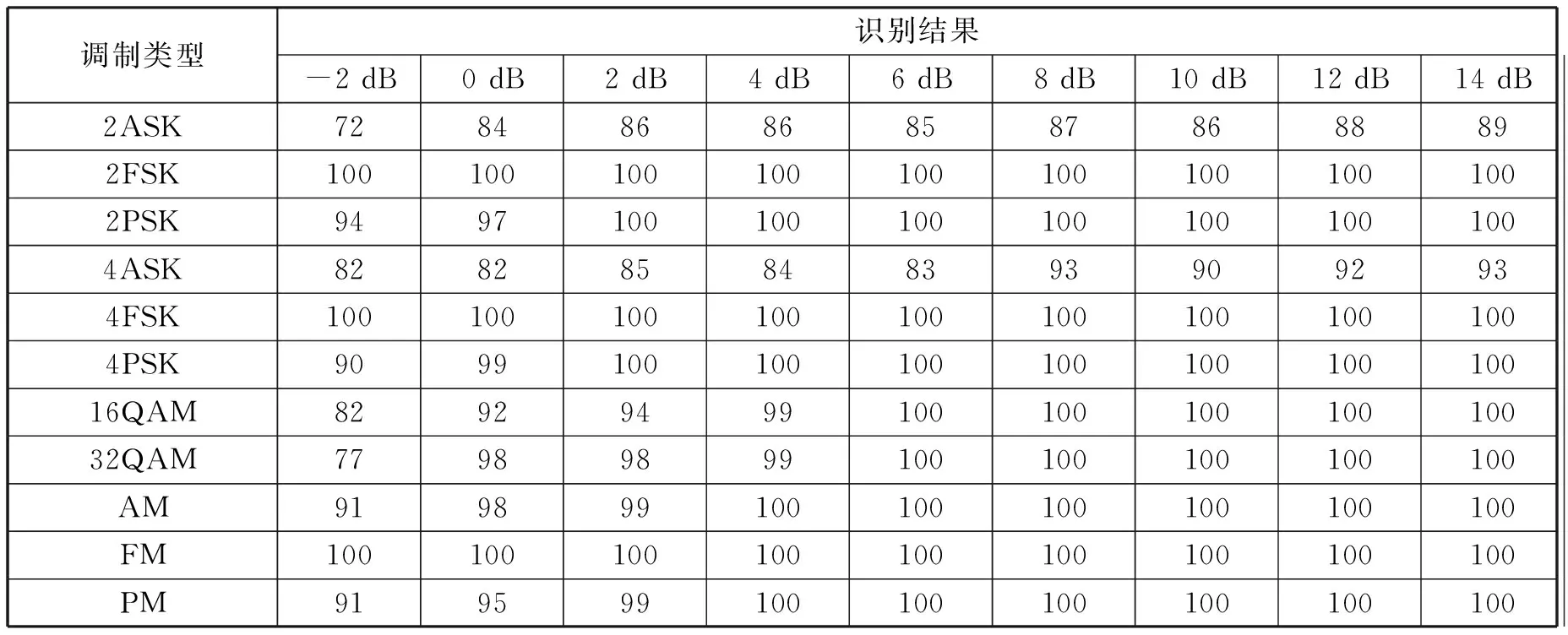
表1 總體識別率

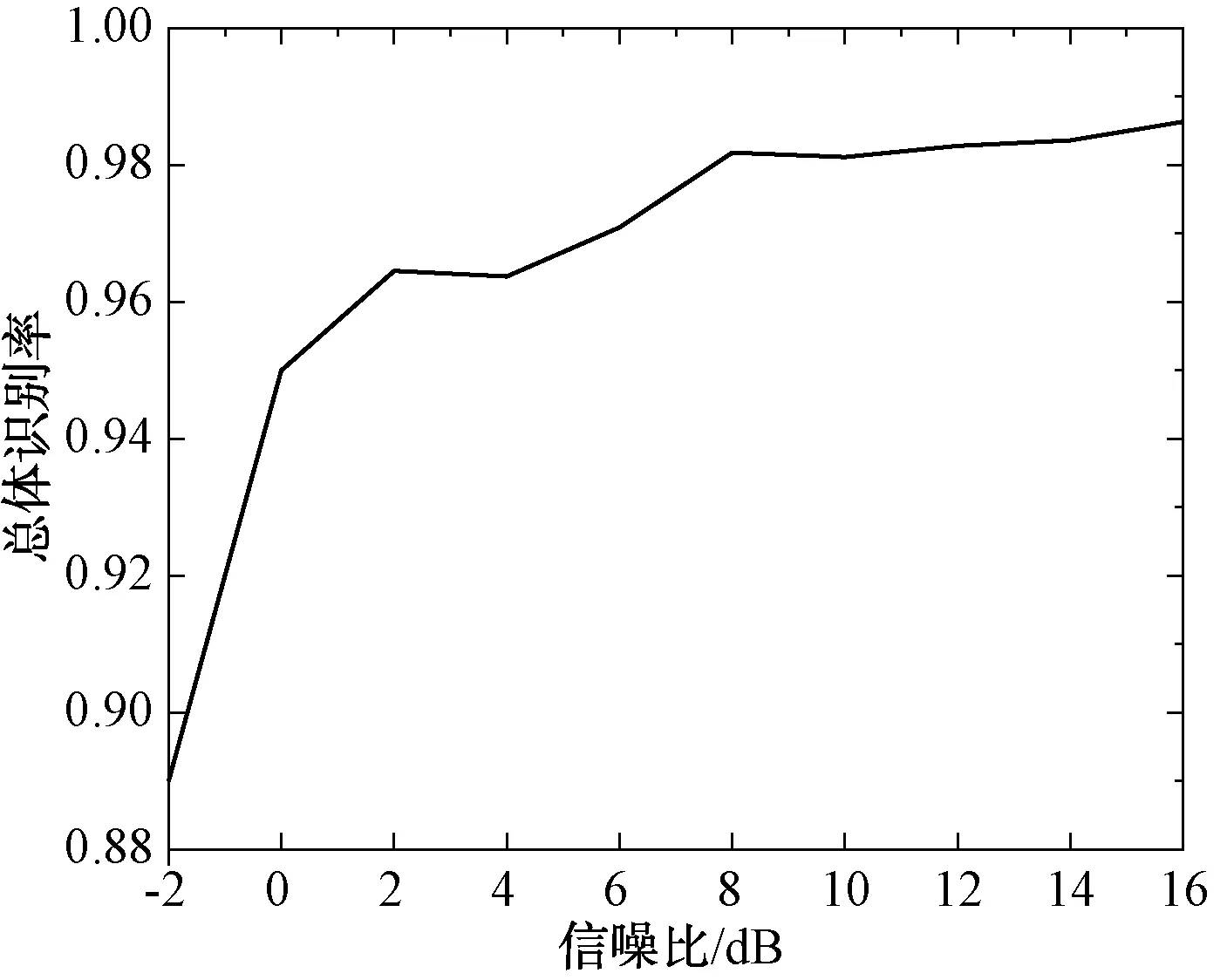
圖4 GA-ELM總體識別率

為了找到2ASK,4ASK和32QAM這3類信號在低信噪比下識別率低的原因，我們構建了-2 dB、0 dB、4 dB、6 dB、10 dB和16 dB下的混淆矩陣圖，如圖5所示。

由圖5可以清晰地看到，在低信噪比下，2ASK和4ASK信號產生了嚴重的混淆，16QAM和32QAM同樣產生了嚴重的混淆。隨著信噪比的不斷提高，16QAM和32QAM識別率逐漸提高不再產生混淆，而2ASK和4ASK識別率提升不明顯，且混淆依然嚴重。直到16 dB，在其他調制樣式識別率收斂到100%時，2ASK和4ASK依舊存在識別錯誤的情況。分析原因，可能是因為在循環譜估計的過程中，調制信號的部分信息丟失，導致2ASK和4ASK之間區分困難。

文獻[16]中指出，ELM-LRF具有非常快的訓練速度。為了驗證本文算法的運行速度，在訓練集和測試集上進行100次試驗，分別對總的訓練時間和測試時間取平均。表2為在1臺CPU為I7-9 700 kHz，內存48 GB的電腦上本文算法的實際運行時間情況。

表2 算法運行時間

由表2可知，相比于深度學習少則十幾個小時、多則好幾天的學習時間，ELM-LRF具有極快的訓練速度，在幾分鐘以內就能學習到數據的內在特性。

5 結束語

本文提出了一種基于循環譜和ELM-LRF的調制識別算法，所用的ELM-LRF網絡是一種基于CNN架構的網絡，具有深度學習的功能，因此它能夠自動地從循環譜圖中提取特征，避免了人工提取特征的過程。同時本文對11種調制信號進行了分類識別，在0 dB時的識別率達到了95%，驗證了算法在低信噪比下對模擬調制和數字調制信號都具有較高的識別率，同時，算法對于16QAM和32QAM等高階調制樣式具有很高的識別效果。此外通過實驗驗證了ELM-LRF具有極快的訓練速度。與文獻[10]中的方法進行對比，本文使用的樣本量更小，獲得的識別率更高，而且相對于傳統深度學習方法，本文算法還具有極快的訓練速度、較大的應用潛力。下一步工作將對64QAM、128QAM和256QAM等高階調制樣式進行實驗。

圖5 算法在-2 dB、0 dB、4 dB、6dB、10 dB和16 dB下的混淆矩陣圖