微信理財通收益率的ARIMA 模型構建及預測

牛孝榮

一、 引言

互聯網金融理財產品因其便捷性已逐漸成為人們日常生活中的一部分，年輕用戶紛紛將自己的存款從銀行取出，購買招財寶、余額寶等金融理財產品。 2014 年，微信理財通正式進行公測，安全卡贖回、理財產品多種選擇、定時定額自動買入、靈活極速贖回等優勢吸引了眾多理財用戶。 隨著時間的推移，資產配置的調整，理財通收益率呈現整體下滑的趨勢，總體來看理財通收益率波動較大，這也就意味著該產品具有較高的風險水平。 對微信理財用戶來說，關注收益率動態就能及時調整理財方案以獲得較高的收益。

對于互聯網金融產品的研究，國內外大多集中于與傳統金融理財的對比分析、互聯網金融產品的理論和發展現狀等。一些文獻的定量分析則關注互聯網金融風險的測定和收益率波動的發展。 李梅以余額寶和零錢寶兩種互聯網金融理財產品為典例，分析了互聯網金融理財產品的安全性和流動性風險。 豐劍簫對余額寶的發展狀況、市場形勢、盈利模式和可能存在的風險等問題進行了詳細闡述。 趙夢佳通過對理財產品的特征分析構建產品收益序列的ARIMA－GARCH 模型，并應用于探究產品收益波動隨時間的發展變化情況。 王明哲等人以余額寶為例研究了互聯網金融產品過去的發展變化并建立時間序列模型進行未來預測。 通過閱讀大量的文獻，理財用戶更關注于互聯網金融產品短期內是否獲得高收益，因此對收益率發展趨勢的研究有著重要意義。 自回歸移動平均模型能夠較好地識別歷史數據的變化趨勢，對未來發展變化進行有效預測。 本文根據時間序列的預測方法，對微信理財通——華夏財富寶的七日年化率進行分析并構建ARIMA 模型，對短期內的理財通收益率發展進行預測。

二、 數據的選取與統計特征分析

通常使用七日年化率和日萬份收益衡量貨幣基金的收益率，而七日年化率能夠平滑的表現貨幣市場的收益率，波動性小于萬份收益。 本文選取微信理財通——華夏財富寶2014 年1 月26 日～2019 年11 月24 日的七日年化率作為研究樣本， 2019 年11 月25 日～2019 年11 月27 日的收益率數據作為測試樣本(數據來自Wind 數據庫)，通過計算得到其統計特征見表1。

表1 描述性統計

由表1 可知，華夏財富寶的均值為3.70，表明該產品具有良好的收益特征。 由于R 語言中沒有直接計算偏度和峰度的函數，因此需加載moments 安裝包，調用skewness 和kurtosis 分別計算。 結果顯示偏度大于0，表明該時間序列均值左側的離散程度比右側弱，為右偏。 峰度大于3，表明該時間序列的曲線峰值比正態分布的高，即尖峰分布。 根據時間序列圖(圖1)，直觀上可知收益率曲線趨勢是波動下降的，ADF 檢驗結果P值為0.09124，說明時間序列未能通過單位根檢驗，則原序列是不平穩的時間序列。

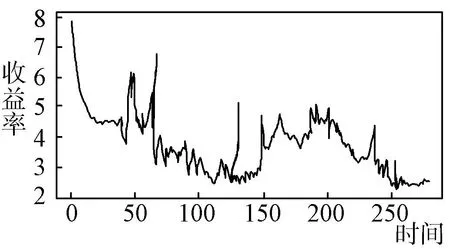
圖1 華夏財富寶七日年化收益率

三、 構建ARIMA 模型

(一)平穩化處理

ARIMA 模型要求輸入的是平穩時間序列，因此需對原始序列進行平穩化處理，可通過差分變換使其滿足平穩性條件。 調用包含在forecast 包中的ndiff()函數快速得出差分次數為1，表明一階差分即可消除線性趨勢。 利用tsdisplay()函數做出一階差分的時序圖，自相關圖以及偏自相關圖，結果顯示一階差分的時序圖相對平穩，并且圍繞0 值上下波動，是否為平穩序列還需進行單位根檢驗。 在R 語言環境下調用tseries 包中的adf.test()函數對一階差分序列進行檢驗，檢驗結果得p－value＝0.01＜0.05， 拒絕原假設，即一階差分的時間序列為平穩序列。 由于純隨機性時間序列的歷史數據不能提供關于未來的信息，因此正式建模之前需檢驗時間序列是否為白噪聲。 利用Box.test()函數進行白噪聲檢驗，統計量p值小于0.05 表示數據是隨機的可能性不大，故一階差分序列為非白噪聲的平穩時間序列，具有建模的價值。

(二)模型的識別

對于ARMA 模型的選擇可根據自相關系數和偏自相關系數。 經平穩化處理之后，AR(p)模型的自相關系數是隨著k的增加而呈現指數衰減或者震蕩式的衰減，偏自相關系數是p階截尾的。 MA(q)模型的自相關系數在q步以后是截尾的，偏自相關系數一定呈現出拖尾的衰減形式。 ARMA(p，q) 模型是AR(p)模型和MA(q)模型的組合模型，因此當平穩序列的偏自相關和自相關系數都是拖尾的，則序列應選擇ARMA 模型。

通常，ARMA(p，q)過程的偏自相關圖可能在p階滯后前有幾項明顯的尖柱，但從p階滯后項開始逐漸趨于0；而它的自相關系數則是在q階滯后前有幾項明顯的尖柱，從q階滯后項開始逐漸趨于0。 為確定p，q的最優選擇，可以采用AIC 準則對模型進行定階。 AIC 準則為赤池信息量，是判斷模型擬合效果的重要指標，其統計量AIC ＝2k－2ln(L)，使用方法是尋找可以最好的解釋數據但自由參數最少的模型，因此應優先考慮AIC 值最小的模型。

(三)參數的確定

通過以上分析，一階差分后的時間序列為平穩序列，因此差分次數可確定為d＝1。 通過判斷自相關圖和偏自相關圖的拖尾和截尾特征確定相對合適的p，q取值。 由R 語言程序導出的一階差分自相關圖(ACF)可以看出除了第1、6、16 階的自相關系數在兩倍標準差的范圍外，其他階數的自相關系數都在范圍內；對于偏自相關(PACF)除了第1、2、5 階的系數在兩倍標準差范圍外，其他階數的偏自相關系數也都在2 倍標準差范圍內，因此可知模型的階數有較多的可能取值，即p＝1，2，5，q＝1，6，16。 使用函數auto.arima()可進行自動定階，通過嘗試不同的階數組合并挑選出可能的最優模型。 為驗證自動定階的準確性，通過arima(huaxiats，order＝c(p，d，q)) 獲取不同階數的ARIMA 模型對應的AIC 值，其中ARIMA(5，1，6)的AIC＝353.53 值最小，這與自動定階的結果是一致的，因此最優模型的階數即可確定，即p＝5，q＝6。 使 用 極 大 似 然 估 計 法 進 行 參 數 擬 合，M1 ＜－arima(huaxiats，order＝c( 5，1，6)，method＝“ML”)可獲得模型的參數估計結果，最終可得模型形式如下:

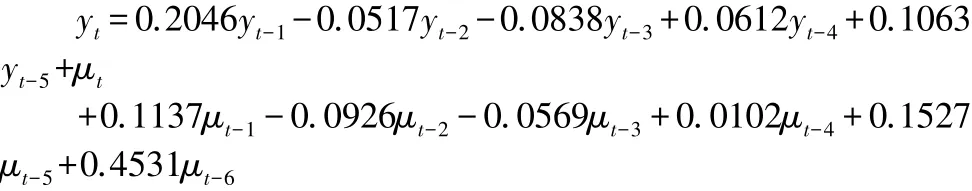
其中，μt是白噪聲過程。

(四)模型檢驗

為驗證模型的選擇是否恰當，檢驗模型的殘差序列是否為白噪聲。 若殘差序列為白噪聲，表明原序列中的信息已被有效提取，模型選擇較為合理。

首先，對殘差序列做正態性檢驗，做出殘差Q－Q 圖，具體程序為:qqnorm(model1 ＄residuals)和qqline(model1 ＄residuals)，輸出正態分位數圖，Q－Q 圖中殘差的散點圖是在直線y＝x附近分布，說明殘差基本符合正態分布。 其次，對殘差序列的自相關性進行檢驗，函數tsdiag()可列出標準殘差時間序列圖、自相關性ACF 檢驗和白噪聲Box.test 檢驗的結果(圖2)，可知殘差的標準差都在0 值上下波動，沒有其他趨勢。 自相關系數都為0，且Ljung－Box 的值都在0.05 之上，即殘差不存在自相關性。 由殘差診斷結果可知，原始數據中的有效信息已經被充分提取，該模型的選取較為恰當。

圖2 殘差診斷

(五)預測分析

為驗證模型預測的準確性和有效性，利用x. fore＜－forecast(model，h＝3)語句對2019 年11 月25 日～2019 年11 月27 日的理財通收益率進行預測，得到未來三日收益率分別為2.515、2.510 和2.508，并將預測值與實際觀測值進行對比，計算可知，模型預測值與實際值有些差距但差距不大，平均相對誤差百分比為4.27%，即預測相對誤差在4%左右波動，說明ARIMA(5，1，6)的構建是合理的，可用于收益率的預測。 同樣，通過forecast()函數可得出2019 年11 月28 ～2020 年1 月28 日的收益率值，plot(forecast())函數做出相應的趨勢圖(圖3)，從預測結果可以看到，收益率預測值在2.45附近波動，說明在預測時期內理財通收益率是比較穩定的，可推測預測誤差應為4%左右，但由于沒有考慮到其他突發情況的發生，具體誤差值還需結合實際收益率進行對比。

ARIMA(5，1，6)模型的預測結果:

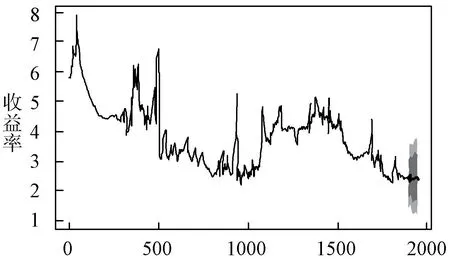
圖3 2019 年11 月28 日～2020 年1 月28 日收益率預測圖

四、 結語

ARIMA 模型是時間序列分析中一種有效的短期預測方法。 通過差分將原始序列進行平穩化處理，其優勢在于平穩時間序列的行為并不會隨著時間的推移而變化，可以通過該序列過去的行為來預測未來發展趨勢。 以R 語言為數據分析工具，理財通——華夏財富寶的七日年化率為研究數據，基于時間序列分析方法在預測方面的應用建立ARIMA 模型，由于模型的建立依賴于歷史數據而沒有考慮到其他影響因素，如國家調控、金融市場變化等，因此模型只適用于短期預測，預測數據并不代表實際數據。 隨著預測時間的延長，預測結果的誤差將逐漸增大。 不過，仍可根據預測結果大致判斷理財通收益率的未來走勢，以便理財用戶及投資方等做出預先評估，優化理財產品收益，規避理財風險。