巧用課本例題結論解決一類切線問題

李昌成 陳 潔

(新疆烏魯木齊市第八中學 830002)

在2001版人教版全日制普通高中數學教材第二冊上冊第75頁中有一個普普通通的例題，當然很難引起大家的重視，但是這道題卻蘊含著深邃的數學思想方法，在高考中經常大顯身手，很可惜一些同學并不知曉，更談不上靈活應用.

一、例題回顧

例題已知圓的方程是x2+y2=r2，求經過圓上一點M(x0,y0)的切線方程.答案是x0x+y0y=r2.解答比較簡單，此處從略.

二、結論推廣

例題中的切線方程可以看成把圓方程中的x2換成x0x，y2換成y0y，常數不變，得到的.推而廣之，對于圓錐曲線(圓、橢圓、雙曲線、拋物線)有下面結論：

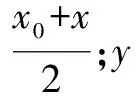
三、結論應用

1.應用于求直線方程

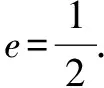
(1)求橢圓E的方程；

(2)求∠F1AF2的角平分線l的方程；

(3)略.

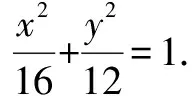
評析使用結論解答此題有效避開了直線和橢圓聯立的二元二次繁雜運算，直接進入一元一次的運算，解答簡捷明快.

(1)求直線AB的斜率；

(2)設M為曲線C上一點，C在M處切線與直線AB平行，且AM⊥BM,求直線AB的方程.

解(1)易得直線AB的斜率為1.

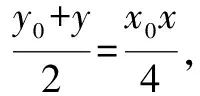
評注結論讓動點M坐標快速明確化，減少變量，使題目難度下降，僅剩一個變量，利用方程的思想，待定直線AB的縱截距，題目得到完美解答.否則將陷入兩個變量，一個方程的僵局.

2.應用于求參數取值范圍

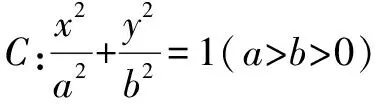
(1) 求橢圓C的方程；

(2) 點P是橢圓C上除長軸端點外的任一點，連接PF1，PF2，設∠F1PF2的角平分線PM交C的長軸于點M(m,0)，求m的取值范圍；

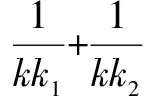
評析從以上這道高考題的解答過程可以看出，恰當運用該切線結論使問題變得直觀形象，這個思路和解法也顯得簡潔明了，避開了純解析幾何……